科学剖析难点 合理解决难点
2015-08-07费建锋
费建锋
[摘 要]教师在思考如何确定教学难点的时候,不仅要考虑知识点的难易程度,更要考虑学生的认知规律、学习起点。只有准确了解、把握学生的学情,才能确定教学中的难点,让学生“不仅知其然,而且知其所以然”。
[关键词]数学教学 教学难点 教学重点 知识结构 原有经验 算理 技能
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2015)20-034
如何科学、合理地确定课堂教学中的难点?笔者通过对“一个数除以分数”的教学,从找准难点、剖析难点到解决难点的思路做了实践研究。
一、找准难点,分析难点缘由
1.认识教学内容在教材中所处的地位
“一个数除以分数”是小学数学教材中最后一种基本计算,也是后面学习小数四则混合运算和分数、百分数等应用题的重要基础。一个数除以分数包括整数除以分数和分数除以分数两种情况,但不论哪一种情况,计算时都要把除以分数转化为乘以这个分数的倒数。
2.认清学生的原有经验
学生在学习新知之前,已经具有分数除以整数的计算概念及之前学习分数乘法的经验,所以“一个数除以分数的计算法则”应当是教学的重点。
3.确定教学的难点问题
要想真正了解学生的学情,还要通过课前的预测。笔者设计了以下3道题,作为学生的“预习单”。
(1)请试着计算。
1■÷4= 1■÷■=
(2)请解决问题。
王老师每天坚持锻炼身体,他用■小时走了1■千米的路,照这样算,王老师每小时可以走多少千米的路?
(3)请提出自己的困惑或你想问的问题。
通过对教材的梳理和预学单的检测以及学生反馈出来的问题,分析得到学生理解上的困难问题:为什么一个数除以分数,等于这个数乘以原分数的倒数?为什么一个数除以真分数其商变大?在解决问题时,为什么要用除法进行计算?
二、剖析难点,探究知识结构
1.分数除法意义相关知识的梳理
对于分数除法的意义的探讨,与之相关的知识点主要有整数乘法的意义、乘法逆运算的概念、整数乘法的概念、分数乘法的概念、分数的概念等。关系如下图: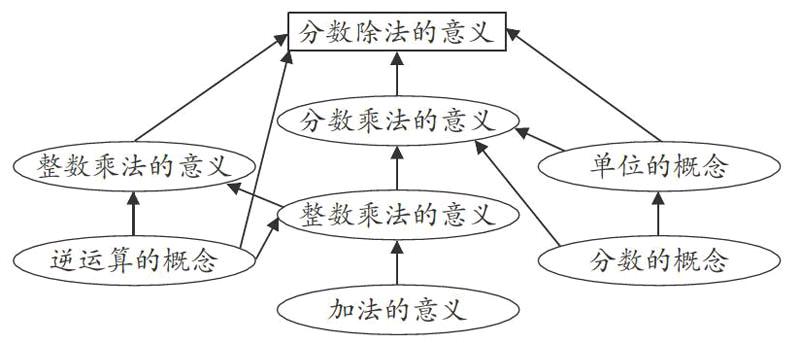
从上图中可以看出,分数乘法的意义是最关键的一个知识点,它是理解分数除法的意义的一个必要基础。如果学生深刻理解了分数乘法的意义,就可以按照这种逻辑去理解逆运算是如何进行的;相反,如果学生对分数乘法的意义不是很明白,分数除法的概念对学生来说就是随意的、难以理解的。所以,为了让学生理解分数除法的意义,课始教师应花点时间和精力,引导学生回顾分数乘法的意义。
2.分数除法意义三种结构的分析
(1)分数除法的包含结构。
尽管包含结构对于整数和分数来说是一样的,但在引入分数时也是需要指明的。在整数除法中,可用“求一个数是另一个数的多少倍”来说明,如8是2的多少倍,由于8除以2得到4,就说8是2的4倍。对于分数也可以这么说,如“■的多少倍是1■”,可以这样来创设情境:“有两条路,A路长1■千米,B路长■千米,问A路的长度是B路的多少倍?”这里就可以用1■千米除以■千米得到6。然而,当被除数比除数小时,这个除法的包含结构需要修改一下,即在原来叙述的基础之上,应该加上“求一个数是另一个数的几分之几”。
(2)分数除法的等分结构。
除法是乘法的逆运算。分数的乘法是已知一个表示整体的数,要求一个表示它部分的数。在分数除法中,表示整体的那个数是我们要求的未知数。例如:“一根绳子的■是1■米,那么绳子的全长是多少?”已知一部分绳子长1■米,也知道这部分是整根绳子长的■,可把1■米看成是这个数的一部分,这样就能很快得到绳子全长6米。
(3)因数和乘积的结构。
即在已知积和一个因数的条件下,求另一个因数,如“求乘■得积为1■的因数”。作为乘法的逆运算,除法是在已知乘积和因数的条件下去求另一个因数,从这个角度来说,可以这样来描述:假设积是1■,一个因数是■,求另一个因数是多少?
3.分数除法运算的算理分析
(1)利用“商不变的性质”来解释算理。
在此之前学生已经学过商不变的性质,在整数除法中,当被除数和除数同时乘或除以一个相同的数,商保持不变。如15÷5=3,所以(15×2)÷(5×2)=3、(15÷2)÷(5÷2)=3。那现在如果被除数和除数同时乘以除数的倒数,这时除数就变成了1,因为除以1不会改变大小,可以忽略。所以,等式就变成了被除数乘除数的倒数,如1■÷■=(1■×■)÷(■×■)=(1■×■)÷1=1■×■=6。
(2)利用“分数等价于除法”来理解算理。
学生学习分数与除法关系时,已经知道分数等价于除法,而且已经学会如何去括号和添括号及交换律。为此,分数除法又可以重新进行书写,如1■÷■=1■÷(1÷4)=1■÷1×4=1■×4÷1=1■×4。
三、解决难点,设计有效教学
1.创设有效情境,帮助学生理解意义
可在同一个主题下创设不同的情境,让学生理解除法的意义,如“王叔叔■天时间耕地1■亩,按照这个速度,一整天可以耕地多少亩”“昨天我骑自行车从A镇到B镇,花了1■小时,完成了行程的■,行完整个路程需要多少时间”等,然后让学生说一说每道题的意义,并想一想问题中具体量的大小,最后列式解决问题。
2.优化学习策略,丰富学生数学技能
验证:为什么除以一个分数等于乘这个分数的倒数?
(1)猜想,通过提供的情境,猜想除法的运算。
(2)动笔,根据题目的意义,动笔画出线段图。
(3)归纳,进行“图”和“式”对照,总结算理。
3.内化知识结构,提升学生思维品质
学生通过猜想和归纳,初步感知分数除法的算理,这时候再加以联系其他的知识结构,帮助其理解算理,这样学生的学习就会事半功倍。
通过这样的教学实践研究,使笔者感悟到,计算教学应该舍得花时间,让学生经历计算方法的探索过程,使学生真正掌握算法,提高计算能力。
(责编 蓝 天)
