数形结合 理解概念

牛献礼

[摘 要]通过分析、对比、概括、推理等活动，让学生体会小数与生活的密切联系，并初步渗透数形结合思想和极限思想，培养学生的思维能力，增强学生对数学的理解和应用数学的信心。

[关键词]小数的意义 教学设计 数形结合

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2015）20-011

【教学内容】苏教版小学数学五年级上册“小数的意义”

【教学目标】

1.了解小数的产生源于需要，“数形结合”探究小数与分数、整数的内在联系，理解小数的意义，会用小数表示数轴上的点，认识小数的计数单位及相关进率，体会计数单位的拓展。

2.通过分析、对比、概括、推理等活动，培养学生的思维能力，初步渗透数形结合思想和极限思想。

3.体会小数与生活的密切联系，增强对数学的理解和应用数学的信心。

【教学重点】理解小数的意义，认识小数的计数单位和进率。

【教学难点】理解小数的意义。

【教学过程】

一、唤醒旧知，引入新课

出示“生活中的小数”：

让学生试着读出1.41和5.98这两个小数。

师：小数的读法跟整数有点区别，在读小数点右边的部分时，要一个数字一个数字地逐个读出来，就像读电话号码一样。

师：乐乐的身高是1.41米，说明他的身高比1米多又不够2米，就用小数1.41来表示。牛奶的价钱是5.98元 / 盒，5.98元是多少钱呢？

生1：5元9角8分。

师：牛奶的价钱比5元多，又不够6元，就用小数5.98元表示。生活中，在进行计算和测量时，往往不能得到整数的结果，这时常用小数来表示。

师：今天学习的是小数的意义（板书），什么是“意义”呢？我特意请教了一位知识渊博的老师——《现代汉语词典》。在《现代汉语词典》的第1546页查到了对“意义”的解释：①“表示的内容”②“价值；作用”。什么是价值呢？就是为什么要学习它。刚才我们已经有了体会，当测量和计算的结果不能用整数表示时就要用到小数。我们这节课就重点来研究“小数表示的内容”。

【思考：有效的教学建立在学生的已有知识和经验基础之上。课始的交流，唤醒学生对小数的已有经验和知识，而通过介绍《现代汉语词典》中“意义”的解释，向学生传递一种足以受益终身的学习方法，体现了“授人以渔”的大学科教育观。】

二、理解小数的意义

1.理解零点几的意义

师（出示一个正方形）：如果这个正方形用整数1来表示，你能画图表示出0.1吗？

生1：先画一个正方形，再把正方形平均分成10份，一份就是0.1。（如图1）

师：把一个正方形平均分成10份，这样的一份还可以用哪一个数来表示？

生2：十分之一。

师：所以，0.1就表示十分之一，这就是小数0.1的意义。（板书）（显示：依次把其中的2份、3份、4份涂色，让生说出相应的小数和它表示的意义。）

（板书：0.2表示十分之二；0.3表示十分之三；0.4表示十分之四……）

师：还可以往下继续，这些话如果用一句话来概括，可以怎么说呢？

生3：0点几表示十分之几。（板书）

师：在0点几中，谁最小？（0.1）0.1也就是十分之一，就是零点几的计数单位。现在如果把平均分成的10份全部涂上色，涂色部分是几个0.1？（10个）也就是几？（板书：10个0.1就是1）

2.理解零点几几的意义

让学生尝试画图表示0.13，然后全班交流。

生4：把一个正方形平均分成10份，先把其中一份涂色，再把第二份平均分成10份，把其中的3份涂色，合起来就是0.13。（如图2）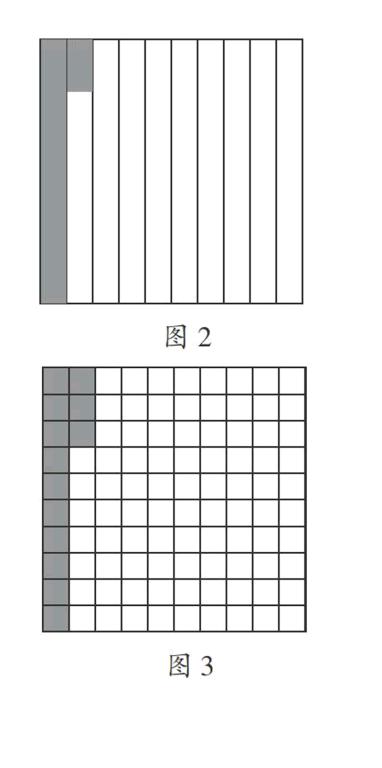

生5：把一个正方形平均分成100份，其中的13份就是0.13。（如图3）

师：把一个正方形平均分成100份，这样的一份是几？

生6：0.01。

师：0.01也就是百分之一（板书：0.01表示百分之一），这就是0.01这个小数的意义。那么，0.13表示什么呢？

生7：0.13表示百分之十三。（板书）

师：0.65表示什么？

生8：0.65表示百分之六十五。（板书）

师：如果用一句话来概括，可以怎么说呢？

生9：0点几几表示百分之几几。（板书）

师：零点几几的计数单位是什么呢？（0.01）

师（显示：0.10和0.1的图示）：看图比较一下0.10和0.1，你有什么发现？

生10：我发现0.10和0.1一样大。

师：是的，0.10=0.1，0.10里面有10个0.01，所以——

生11：0.1里面也有10个0.01。（板书）

3.认识零点几几几

师：零点几就表示十分之几，零点几几就表示百分之几，根据这两句话，你能推出第三句话吗？

生12：零点几几几就表示千分之几。（板书）

师：这是我们推理出来的，凡是推理出来的还需要做一件事儿，就是“验证”。（显示：把一个正方形平均分成1000份，将其中的一份涂色）

生13：0.001表示1 / 1000。（板书）

（结合图示，逐步归纳：0.002表示2 / 1000；0.003表示3 / 1000；0.004表示4 / 1000；……）

师：0.001就是零点零零一，10个0.001是0.01。（板书）

师（归纳）：小数就是表示十分之几、百分之几、千分之几……的数。

【思考：有效地利用已有知识经验，启迪学生进行探索和发现。此处的正方形作为思维表象的载体，通过平均分形象地展现小数形成的过程，并为学生提供了有效理解小数意义的表象模式。借助直观的图示，沟通小数与十进分数（分母是10、100、1000……）的内在联系，把小数的概念建立在十进分数的基础之上，使学生在与分数的联系中理解小数的产生，初步理解小数的意义。】

4.用数轴上的点表示小数

出示：数轴

师：这是一条带方向的直线，数学上叫做“数轴”。任意一个小数都能用数轴上的点来表示，箭头向右，表示从左往右，数轴上的数越来越大。怎么用数轴上的点表示0.6呢？

生14：把0到1这一段平均分成10份，取其中的6份就是0.6。（课件演示：在数轴上表示出0.6。）

师：0.61应该在哪里呢？要准确地找到它的位置，应该怎么办呢？

生15：把0到1平均分成100份。

生16：也可以把0.6到0.7平均分成10份。

师：把0.6到0.7这一段平均分成10份，其实就相当于把0到1这一段平均分成了100份。（课件演示：把0.6到0.7这一段放大后，再平均分成10份，表示出0.61）

师：如果要在直线上表示0.618呢？

生17：再把0.61和0.62这一段平均分成10份。

师：也就是把0到1平均分成——

生18：1000份。（课件演示：把0.61到0.62这一段放大后，再平均分成10份，表示出0.618）

师：如果我们想表示得更精确，还可以怎么办？

生19：继续分下去。

师：想一想，0和1之间有多少个小数？

生20：无数个。

师：0.6和0.7之间呢？

生21：也是无数个。

生22：任何两个数之间都有无数个小数。

师（追问）：为什么？

生23：因为还可以一直分下去。

师：没错！还可以无限地分下去，就会有无数个小数。这里我向大家隆重介绍0.618这个小数，0.618是一个非常神奇的小数，大家可以课后了解这个小数。

【思考：借助“数轴”这一直观模型，数形结合，从整数到一位小数，再从一位小数到两位小数，再到三位小数，让学生直观感受到一个不断细分的过程。学生通过观察不断细分的数轴，能感受到小数表示数的精确性，感悟到用更小的计数单位可以进行更精确的表示。】

三、巩固应用，深化理解

1.“数数”练习

介绍：数学家华罗庚的名言“数是数出来的”。

（1）以0.1为单位数数

结合图示，让学生依次数出0.1、0.2、0.3、0.4。

显示：0.4的计数单位是（ ），它有（ ）个这样的计数单位，再添上（ ）个这样的计数单位，就是1。

（2）以0.01为单位数数

结合图示，让学生依次数出0.01、0.02、0.03、0.04、0.05、0.06、0.07、0.08、0.09、0.10、0.11、0.12。

显示：0.12里面有（ ）个0.01，还可以说0.12是由（ ）个0.1和（ ）个0.01组成的。

结合图示，让学生依次数出：0.97、0.98、0.99、1、1.01、1.02、1.03。

1.03里面有（ ）个0.01，还可以说1.03是由（ ）个1和（ ）个0.01组成的。

2.写出数轴上箭头所指的数

0.4 （ ） 1.3 （ ） （ ）

■

【思考：“数数”活动是学生形成“数概念”的基础，没有“数数”这一过程，学生对“数”的理解是不深刻的。通过观察图形中直条的累加，也就是计数单位的不断累加，不断形成新的小数，学生按照计数单位一个一个地数数的过程中，感知小数的组成。在遇到“拐弯数”时，教师应放慢速度，不断加强演示，让学生直观感受到“满十进一”，为学生掌握数的组成和相邻计数单位之间的十进制关系提供了形象的支撑。】

四、全课总结

（责编 金 铃）