铁路空车调配的多时点优化模型研究

王波，荣朝和，黎浩东*，王保华

（1.北京交通大学经济管理学院，北京100044；2.广铁集团惠州车务段，广东516023；3.IBM中国研究院，北京100193）

铁路空车调配的多时点优化模型研究

王波1,2，荣朝和1，黎浩东*1，王保华3

（1.北京交通大学经济管理学院，北京100044；2.广铁集团惠州车务段，广东516023；3.IBM中国研究院，北京100193）

空车调配优化直接影响铁路运用车辆使用效率和市场需求满足的程度.从实时性优化调整角度，通过定义配空弧与装运弧，确立了配空和装运之间的映射关系，从而形成空车调配服务时空网络.在此基础上，综合考虑决策阶段内收益、成本、服务能力等因素，以空车调配收益最大为目标，构建空车调配的多时点优化模型.最后以粤东地区空车调配为案例，对所构建模型进行验证.案例结果表明，所提出的空车调配时空网络构建方法，有助于综合考虑收益、成本和点线能力等因素，以及降低问题的难度，可为空车调整策略提供新的思路.

铁路运输；空车调配；服务时空网络；多时点；列车开行

1 引言

无论为适应市场发展采取何种铁路货运改革形式，空车调配始终是铁路运输组织中的重要问题之一.国内外学者对空车调配问题进行了很多研究.在国内，从建立模型的策略上看，文献[1-4]分别从空车调配多阶段优化、车种代用情况下空车调配、车数最少空车调配、基于知识约束空车调配等角度进行优化研究；从模型求解上看，文献[5-8]分别从应用重心优化方法、遗传启发算法、振荡法对空车调配问题进行求解；国外，文献[9-10]以市场需求的满足为目标，研究了空车调配随时间段变化的情况等.在上述建模中，存在着诸如编制方法静态局限、排空与配空未统筹兼顾、空车调配与列车开行计划及其调整不协调等不足，这可能导致所编制的空车调配方案难以实施.本文从铁路运输调度实际工作出发，从实时性优化调整角度，在决策阶段内综合考虑收益、成本、服务、能力等因素，建立铁路装卸站时点之间映射关系，从而形成铁路多时点空车服务时空网络；在时空网络中，节点的设置体现各装卸站点的作业时间点，协调排空和配空关系；联弧则是基于实际列车开行计划设置，是空车调配的具体反映；最后基于时空网络，从动态优化角度建立铁路局（公司）管内空车调配的多时点优化模型，并通过具体案例对模型进行验证.

2 服务时空网络和模型建立

2.1 建立映射关系

决策阶段的时间长短取决于运输确定性信息的掌握情况，掌握的越好，决策阶段时长就越长，否则，不确定因素越多，决策时长就越短.如图1所示，在A站的A1时点有一组车卸空，在技术作业完毕后其中一部分可运送到C1时点进行装车，装车后在技术作业完毕挂运到B站的B1时点进行卸车，卸车完毕后再经装车等作业挂运到A站的A3时点；另外一部分，可在本站等到A2时点进行装车，在相关作业完毕后再挂运到C站.在上述过程中，相关运输信息可以通过推流、各种作业标准和列车开行方案等方面取得.在取得决策阶段相关信息、开行计划后，可通过联弧形式建立映射关系，其中映射关系是指实际空车组织的实际作业过程（包括主要的装卸作业时间点和空车调配过程）在时空网络中的具体表示.其中时空网络中的节点表示实际的装卸作业时间节点，联弧则是基于实际运营计划设置的可能空车调配作业，包括配空弧和装运弧两种.在重车卸空完毕的时点与该车在所装车站装车时点之间建立联弧，定义为配空弧；在装车时点与该车在所卸车站卸车完毕时点建立联弧，定义为装运弧，如图1所示.所有车流运行、等待和作业状态都可以用配空弧和装运弧来表示.

图1 配空弧与装运弧的形成Fig.1 Construction of empty railcar arcs and loaded railcar arcs

以图2所示网络进行说明，其中A方向是进口接重方向，D站是交口排空方向.通过推流，预计在A站6时（点A6）、B站8时（点B8）、C站12时（点C12），以及E站7时（点E7）有重车卸空；根据请求车情况，在B站11时（点B11）、C站20时（点C20）、D站12时（点D12）有请求装车.在计划开行方案制定后，在所有满足卸车时间、装车时间、技术作业时间、运行时间等之和最小接续时间条件的装车与卸车时点之间，以及满足车种或车种代用要求的联弧之间，建立映射关系.如图3所示，L1表示A站6点卸空车流可配空到B站11点装车的配空弧；L2表示A站6点卸空车流可配空到C站20点装车配空弧；L3表示A站6点卸空车流可经D站进行排空的配空弧；L4表示D站在12点可能的装车向C站挂运的重车卸空后为20点装车配空的装运弧；L5、L6表示C站在20点可能开始装车挂运而形成的装运弧，其他弧亦同.设计算阶段为6:00-24: 00，则所有已知装运时点都应包括在该阶段内，如图B11、C20、D12；如果卸空站仍有空车在站等待或有空车需排空超出计算阶段等情况时，如A站6时A6点的卸空车，对于要等待到下一阶段的空车，可在卸空时点和本站计算阶段终点间建立配空弧如图L7，而A24时点的空车又可作为下一计算阶段的空车源.对于排空到分界口却超出计算阶段的空车，仍可按建弧要求形成配空弧如L3.这样，所有配空弧与装运弧共同构成了一种服务时空网络形态.基于列车运营计划，将空车调配问题用时空网络表示，可将该问题描述为网络流问题，有利于将空车调配与实际列车运营计划相结合，进而有利于对问题的描述、模型的构建及求解.

图2 某管内车站布局示意图Fig.2 Yard layout on a main line

图3 由配空弧与装运弧构成的服务时空网络Fig.3 Time space network based on empty railcar arcs and loaded railcar arcs

2.2 建立优化模型

Lk为配空弧集合，Lz为装运弧集合，i为联弧索引，有i∈(Lk⋃Lz)；N为节点集合，n为索引；T为时点集合，t为索引.n站t时节点所连结的配空弧集合为分别是以此节点为终点、起点的配空弧集合，有；n站t时节点所连结的装运弧集合为分别是以此节点为终点、起点的装运弧集合，是以此节点为起点的装运弧集合，有；n站t时节点卸空车总量为Qnt，装卸作业能力为Pnt，请求车总量为Znt；n站t时节点i配空弧能力为，i装运弧能力为；fi为i装车弧单车收益，ci为i配空弧或装运弧单车成本.决策变量xi为各联弧流量，为非负实型变量.模型表述如下：

（1）节点流量守恒约束.

对于包含装运弧N站t时点流进量与流出量相等，有

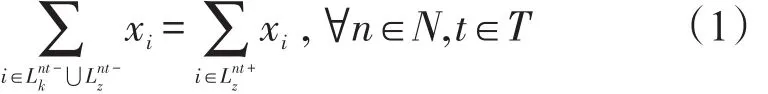
对于不包含装运弧N站t时点卸空车总量等于配空弧总流量，有

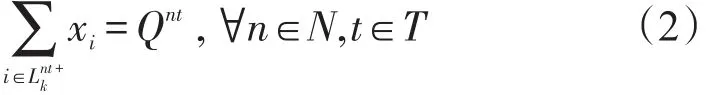
（2）N站t时的作业量不大于其装卸作业能力，有

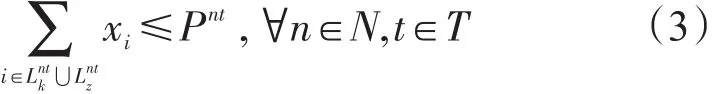
（3）配空流量和装运流量分别小于等于弧能力，有

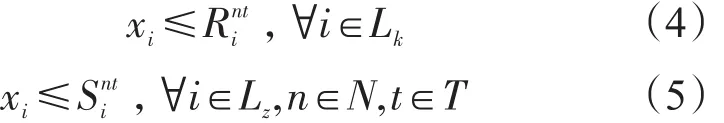
（4）装运弧流量小于等于N站t时需求装车数，有

以最大化空车调配的总收益为目标，表示如下：

关于模型的几点说明：

（1）弧形成的前提是有列车开行计划，列车开行计划是根据决策阶段内运输情况编制出来的，开行计划进一步调整完善可形成日（班）计划中的列车工作计划.

（2）卸空时点和装运时点的确定，体现了时间约束，在卸空时点之前因没有卸空，也就不能形成为配空所需的车组；在装运时点之后不符合开行时间要求，所装车列要在此点编入计划车次.

（3）装车弧收益是指包括运输收入、装卸收入、其他服务性收入在内的收费，是铁路因货运装车而带来的一切收益.

（4）配空弧或装运弧成本是指车辆走行、装卸作业、车辆使用等的费用支出，不同的的车辆走行、装卸作业及使用的车辆种类对应着不同的配空弧或装运弧成本.成本可分为可变成本和固定成本，可变成本主要是车辆走行成本、使用成本等组成，走行成本可综合各种可变费用进行平均分摊求得，使用成本可按铁路总公司车辆使用收费情况获得；对于固定成本在具体计算时，涉及到各种设备实施的折旧，计算相当复杂，但考虑到在短时期内无论是否计入固定成本都不影响决策目标的求取，因而在此可不计入.

（5）配空弧能力是指卸车站与装车站之间有计划安排、符合列车编组要求，且满足最小接续时间条件的最大输送能力，或是在站等待作业时的最大容车数，装运弧能力亦同.

（6）对于重点必保的排空或配空任务要求，在计算时其装运弧收益取值为较大的实数，以优先保证这部分空车的调配.

所构建的模型为整数规划模型，考虑路局层面空车调配问题规模，以及时空网络构建时对问题的简化，可采用Cplex等优化软件进行求解.如在所构建的时空网络中，可通过作业时间的推算、走行径路等的分析，剔除明显不合理的联弧，进而压缩问题的规模.

3 实例分析

以粤东铁路配空为例进行测算，各站点如图4所示，其中东莞东口是接重和空车进入口，龙川北是编组站，定南口是空车排出口，其他各站是货运作业站.

图4 粤东铁路货运站点示意图Fig.4 Yard layout of East Guangdong Railway

在表1中通过推流可预计各站在所列时间点有重车卸空；按货运装车作业时间标准和开行计划可确定装运时间；运输收入是实际收取的装车运费，是按货运品类的货价率计算求得，再按相关优惠政策执行后的最后收费；运行成本是走行成本+车辆使用成本=走行里程×0.8+使用时间×5.7，0.8在本算例中是各种可变费用综合平均求得，是单车每走行一公里所需费用，使用时间=走行里程/平均旅行速度+装卸作业时间.

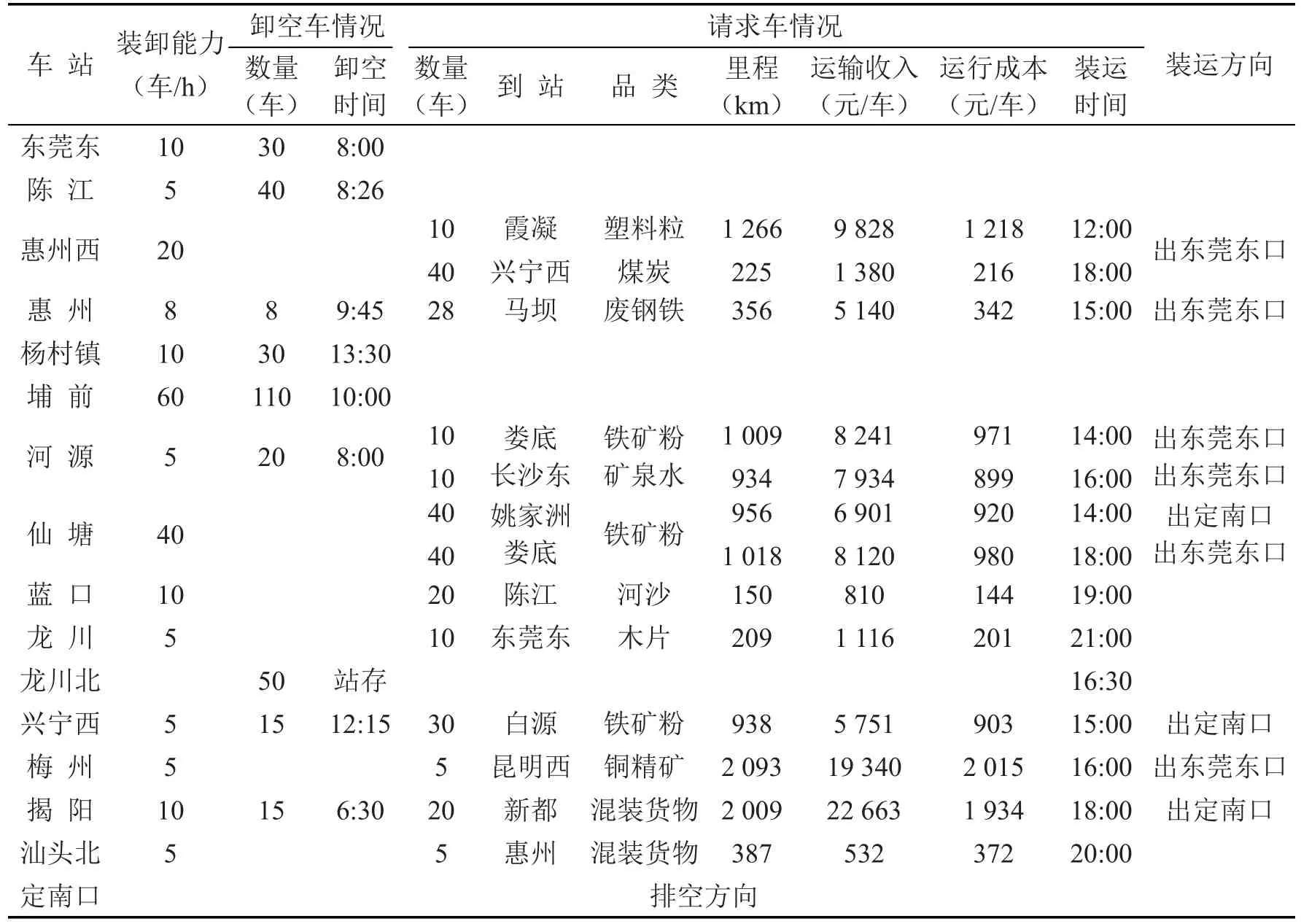
表1 各站卸空车和请求车情况Table 1Unloading and empty car requirement of each yard

图5是部分计划开行列车运行线，货物列车运行线铺画是在旅客列车运行线确定的情况下，根据运输能力和生产实际进行铺画，图中铺画了部分为配空所开行的计划线，装运重车运行线等计划开行线铺画同理.

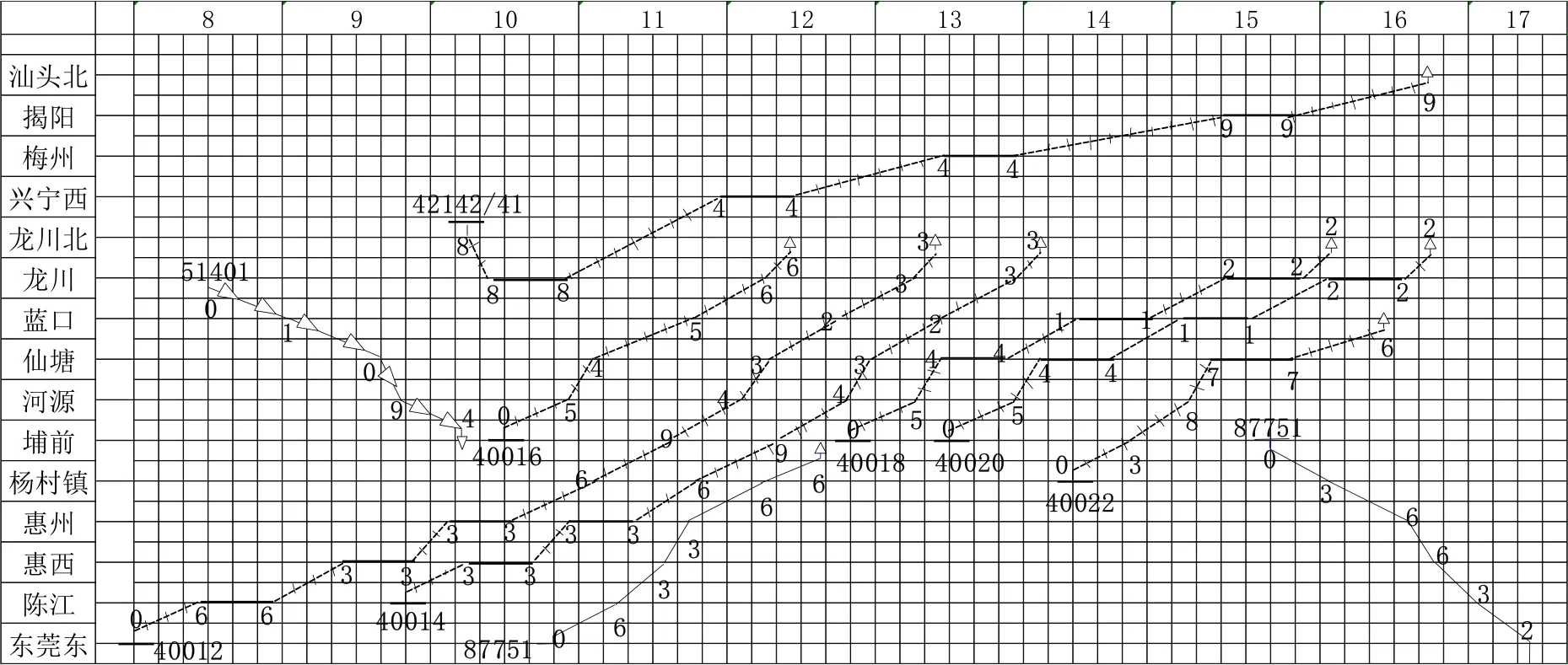
图5 计划开行列车运行图Fig.5 Timetable of freight trains in of East Guangdong Railway

根据上述已知条件，可构建相应的时空网络，这里只给出了如表2所示的配空弧信息.其中线的两端连结卸车站和装车站，弧起点时刻是卸空时间，终点时刻是装运时间，空车总量是卸车站卸空总量，可挂运车次是计划开行列车可能挂运空车的列车.在配空弧构建过程中，根据走行情况和具体作业去掉了明显不合理的联弧，如仙塘配空一般由埔前卸车配空，而不由东莞东、陈江卸空调配.

表2 配空弧构建情况Table 2Information of empty arcs

本模型采用IBM ILOG CPLEX 12.2进行求解，计算结果如表3所示，目标函数值为1 580 394.

表3 配空情况及开行方案Table 3Empty car distribution and trains plan

4 研究结论

（1）对于列车开行计划下的多车种、多去向的配空及装运方式，可采用由配空弧与装运弧构成的服务时空网络形式进行表述，车辆走行、装卸作业、车辆使用等成本构成配空弧和装运弧成本，运输收入、装卸收入、其他服务性收入在内的收费构成装车弧收益，通过求解按效益最大化为目标的函数，能够得出实际应用的满意配空方案.

（2）如果按市场开发及拓展所提出的配空要求，可对模型中的收益进行重新赋值，这时的收益已不是现期收益，而是预期收益或是潜在收益，通过调整收益值能够形成按要求的配空方案，如在案例中对汕头北的装车，因对潜在市场的开发需要进行装车时，按市场营销的预期收入进行当期化处理后，可形成新的满意配空方案.

（3）在列车开行计划下的配空方案形成后，需重新调整列车工作计划，如由于排空比配空到汕头北要优，配空优化结果没有往汕头北配空5个车，所开行的42142/41次列车即到揭阳站截止，又如配空优化结果是40012次列车运行到惠州甩空，因而不会再开行至龙川北，这些都需要重新对列车开行计划进行优化，在此基础上再对空车调配计划进行优化，反复调整才能形成合理满意的工作计划.

[1]梁栋,林柏梁.铁路空车调整的多阶段策略优化模型研究[J].铁道学报,2007,29(1):1-6.[LIANG D,LIN B L.Research on the multi-stage optimization model of empty railcar distribution[J].Journal of China Railway Society,2007,29(1):1-6.]

[2]梁栋,林柏梁,严贺祥,等.车种代用情况下的铁路空车调配研究[J].铁道学报，2005,27(4):1-5.[LIANG D,LIN B L,YAN H X,et al.Study of railway empty car distribution with substitution of empty car types[J]. Journal of China Railway Society,2005，27(4):1-5.]

[3]李文权,杜文,周贤伟.优化空车调配问题[J].西南交通大学学报,1998,33(4):383-386.[LI W Q,DU W, ZHOU X W.Optimal assignment of empty cars[J]. Journal of Southwest Jiaotong University,1998,33(4): 383-386.]

[4]张喜,张全寿.基于知识约束的空车调整优化方法研究[J].铁道学报,2003,25(6):14-20.[ZHANG X, ZHANG Q S.Study on the optimization method of emptywagondistributionbasedonknowledge constraints[J].Journal of China Railway Society,2003, 25(6):14-20.][5]纪嘉伦,林柏梁,李福志,等.用重心优化方法求解铁路网上空车调配问题[J].铁道学报,2001,23(3):109-113.[JI J L,LIN B L,LI F Z,et al.Distribution of empty wagons on railway network by using the centerof-gravity-optimization method[J].Journal of China Railway Society,2001,23(3):109-113.]

[6]熊红云,鲁五一,温红艳.铁路空车调配问题的遗传启发算法[J].中国铁道科学,2002,23(4):118-121.[XIONG H Y,LU W Y,WEN H Y.Hereditary heuristic algorithm for empty car distribution in railway transportation[J].China Railway Science,2002,23(4): 118-121.]

[7]曾健,周健,张喜.空车调整专家系统的研究[J].铁路计算机应用,1999,8(4):5-7.[ZENG J,ZHOU J, ZHANG X.Research on empty cars distribution expert system[J].Railway Computer Application,1999,8(4):5-7.]

[8]果鹏文,禇江,林柏梁.用振荡法解大规模路网上的空车配送问题[J].中国铁道科学,2002,23(4): 111-117.[GUO P W,ZHU H,LIN B L.Reiterative adjusting method of empty wagon on large-scale railway network[J].China Railway Science,2002,23(4):111-117.]

[9]Kikuchi S.Empty freight car dispatching model under freight car pool concept[J].Transportation Research Part B,1985,19(2):169-185.

[10]Glickman T S,Sherali H D.Large scale network distribution of pooled empty freight cars over time,with limitedsubstitutionandequitablebenefits[J]. Transportation Research Part B,1985,19(2):85-94.

Multi-time Point Optimization Model for Empty Railcar Distribution

WANG Bo1,2,RONG Chao-he1,LI Hao-dong1,WANG Bao-hua3
（1.School of Economics and Management,Beijing Jiaotong University,Beijing 100044,China;2.Guangzhou Railway(Group) Corporation,Guangdong 16023,China;3.IBM Research-China,Beijing 100193,China）

Optimization of empty railcar distribution helps to improve the railcar service efficiency and meet the transportation demand.This paper defines empty railcar arcs and loaded railcar arcs from the perspective of real-time optimization,the revenue,cost and service capacity can be denoted on those arcs during the plan horizon.A time space service network of empty railcar distribution is present after mapping the relationship of those arcs.Based on the time space network,a multi-time point optimization model is proposed,with the objective of maximizing the total revenue of empty railcar distribution.At last,the model is verified by a real world example of east region of Guangzhou Railway(Group)Corporation.The result shows that the proposed time space service network and the model can reduce the difficult of the real world problem,and provide a new idea for empty railcar distribution.

railway transportation;empty railcar distribution;time space service network;multi-time point;train operation

1009-6744（2015）05-0157-07

U292.3

A

2015-03-18

2015-05-12录用日期：2015-05-18

国家自然科学基金项目（41171113）.

王波（1974-），男，黑龙江齐齐哈尔人，博士后. ＊

:lihd@bjtu.edu.cn