基于ARMA预测模型的交叉口车辆碰撞风险评估

2015-08-07张良力祝贺吴超仲郑安文

交通运输系统工程与信息 2015年5期

张良力，祝贺，吴超仲，郑安文

（1.武汉科技大学信息科学与工程学院，武汉430081；2.武汉理工大学智能交通系统研究中心，武汉430063；3.水路公路交通安全控制与装备教育部工程研究中心，武汉430063）

张良力*1，祝贺1，吴超仲2,3，郑安文1

车辆进入交叉口前的速度时间序列可用于预测车辆进入交叉口后若干步数速度值，利用车速预测值推算冲突方向车辆在交叉口内的行驶位移及其车间距离，可评估车辆发生碰撞的风险.针对交叉口附近车速分布符合随机序列特征，采用自回归滑动平均(ARMA)理论进行车速时序预测建模，步骤包括时序数据相关性检查、模型p-q定阶、解析式系数估计、适用性检验.试验结果表明：利用实测车速中的前40个时序数据建立ARMA模型，预测出的20个车速值与实测值贴近，冲突方向两车车速归一化平均绝对误差分别为0.006 56和0.003 4；利用全部60个实测数据建立预测模型，检测预测值残差自相关函数发现其绝对值均小于0.258 2，表明所建车速预测方法适用.

智能交通；碰撞风险评估；自回归滑动平均建模；交叉路口；车速预测

1 引言

统计数据显示约30%的道路交通事故发生在交叉口区域[1].即使在交叉口区域设置交通控制信号灯，因车辆提速抢行、闯红灯等违法行为引发的恶性碰撞事故仍时有发生.车辆进入交叉口前的速度信息可作为交叉口车辆碰撞风险评估依据.Spek等研究了驶向交叉口时的车速与碰撞事故发生之间的概率模型，车速与车间可接受间隙之间关联明显[2].Sun等在分析设置抓拍摄像机对车辆闯红灯行为的影响时发现，驾驶人停-进决策两难区(dilemma zone)明显增宽且闯红灯车速比未设置摄像机时要高[3].郭伟等采用斗鸡博弈模型描述了车辆在进入交叉口前的加减速过程[4].

分析已有研究发现，对车辆进入交叉口前的速度进行连续采集并按时间标记(time stamp)排列，所构成的时间序列数据既能反映驾驶人个体驾驶行为特征，也可反映自车与冲突方向其他车辆、行人之间的博弈过程，对其进行分析并预测后续时段内车辆速度，可达到评估车辆在交叉口内发生碰撞风险的目的.本文围绕上述内容开展研究，所用理论为自回归滑动平均(ARMA)预测建模[5]，评估依据和建模数据为待评估对象(自车)与冲突方向车辆(他车)同时驶向交叉口时生成的车速时间序列，建模数据通过实车驾驶试验获得.

2 交叉口车辆碰撞风险评估方法

守法驾驶车辆在进入交叉口之前经历了车速/车道调整、停车等待、放行等阶段，各阶段持续时长、任务单一，且车速已降至驾驶人应急反应时间可控范围内，故能有效降低在交叉口内发生碰撞事故的风险.而以缩短行驶时间为目的的违法驾驶车辆，是在提速基础上实施多任务驾驶操作，驾驶人应急反应时间随之增长，若在禁行周期内抢行进入交叉口，发生碰撞事故的风险升高[6].

假设冲突方向上的机动车1、机动车2在交叉口区域的方位如图1所示.在进入交叉口前的t时刻两车车速分别为v1(t)、v2(t).若其中一车在禁行周期内进入交叉口且两车均未作应急措施时，两车在各自行驶方向的交点处发生碰撞的概率较大，设两车在t时刻与碰撞点之间的距离分别为l1、l2(以车辆平面中心点为测量点).

图1 机动车1、机动车2在交叉口区域方位示意图Fig.1The two vehicles spots at the intersection

由于两车均受交叉口区域交通流量的影响，l1、l2、v1(t)、v2(t)为随机值，假设机动车1在t+kΔt时刻抵达碰撞点，即k值应满足

若已知v1(t)、v1(t+nΔt)(n=1,2,…,k)，通过迭代循环可确定k值；在k值确定的基础上，若v2(t)、v2(t+nΔt)(n=1,2,…,k)可获取，则机动车2距碰撞点距离s为

当s＞0时，机动车1率先抵达碰撞点，当s＜0时，机动车2率先抵达碰撞点，上述情况两车均不发生碰撞；而实际情形中，由于车辆具有体积，当|s|＜(a+b)(a为两车中较长车辆长半值，b为较宽车辆宽半值)时，两车碰撞，故两车在交叉口内发生碰撞的风险评估模型应为

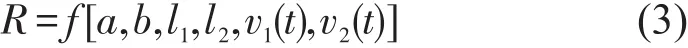
具有地理定位与短程无线通讯功能的车载智能系统可实现交叉口区域内车辆实时状态数据的采集与交换，但在进入交叉口的t时刻前后，车速通常时变且具有明显的随机性，因此碰撞风险也是动态变化的.分析t时刻之前车速变化，预测t时刻之后车速趋势，成为上述风险评估方法的基础.根据交叉口区域驾驶人控制车速行为特征，首先使用自回归滑动平均(ARMA)预测模型对冲突方向两车速度时间序列进行分析与预测，然后根据机动车与碰撞点之间的距离s可达到评估车辆是否具有碰撞风险目的.

3 车辆速度ARMA预测建模

ARMA模型具有随机差分方程的形式[5]，其数学解析式描述如下：

式中φi(1≤i≤p)和θj(1≤j≤q)为模型参数；Xt为零均值随机序列.本文中，Xt即为车辆速度时间序列，εt则是与车辆速度时序对应，且满足驾驶环境条件的高斯白噪声序列.p=0时，式(4)即为MA(q)模型；q=0时，式(4)则为AR(p)模型[7].基于已知车速时间序列建立后续车速预测模型的步骤如下：

实验节点如图1(b)所示，节点采用RouterSationPro嵌入式平台，操作系统是OpenWRT,内核为Linux kernel 2.6.配置了30dBi的高增益定向天线，UBNT SR71-A无线网卡.该网卡能支持3×3 MIMO (Multiple-Input Multiple-Output)，但是实验中受所用天线的影响，只能使用到2×2 MIMO，对应MCS 0-15，其中MCS 0-7为单个空间流，MCS 8-15为2个空间流，下文分别简称为单流和双流.

(1)数据相关性检查.

检查时序数据Xt内散点数据之间的自相关性和偏相关性.通过观察自相关、偏相关函数值分布，若分布曲线符合“拖尾”和“截尾”特征，则表明该序列适合建立ARMA模型.用于相关性判断的自协方差Rk和偏相关函数φk,k计算公式为

若时序数据不满足相关性要求，则需对Xt中用于部分散点数据进行差分、微分或取对数等运算操作，使其变为平稳数据序列时继续后续步骤.

(2)模型定阶.

选取合适的p、q值确立ARMA模型解析式.若时序数据自相关、偏相关函数值分布二者之一具有“截尾”性，即p、q两者之一值为0，另一值不为0，可采用观察法直接从自相关、偏相关函数值分布图中获得；若函数值分布均为“拖尾”性，即p、q均不为0，采用AIC定阶准则确定p、q值，即使下式为最小值.

(3)模型参数估计.

ARMA模型参数估计方法有多种，如矩估计、最小二乘估计等，一般选用计算较精确的最小二乘估计法.

(4)模型检验.

4 应用实例

4.1 实车驾驶试验与数据采集

根据图1所示车辆碰撞情形设计实车驾驶数据采集试验.驾驶区域选在武汉市某一新建市政道路交叉口处，要求交叉口连接道路延伸足够长、视野开阔、车流量小.冲突方向上的机动车1、2采用同一型号小型轿车(车长4.5 m，宽1.8 m)，车速由汽车驾驶行为试验平台每间隔1 s采集1次并按时间顺序保存.为避免机动车1、2真实发生碰撞，保障实车驾驶试验安全，车辆在抵达碰撞点之前必须停止.假定试验车辆在停止之前达到车速最后一个峰值处作为车辆进入交叉口起点，认定该峰值车速为v1,2(t)，目测并记录该点；车辆停止后根据车辆行进方向确定碰撞点位置，测量起点至碰撞点的距离，作为图1中所示l2.回看汽车驾驶行为试验平台车速数据记录，截取用于ARMA预测建模的序列数据区段.

通过实车驾驶试验获得机动车1至碰撞点之间的距离约为30 m，机动车2至碰撞点之间的距离约为32 m.机动车1、2速度时序数据如图2所示.其中单个时序内车速数据60个，按时间逆序分别定义为v(t),v(t-1),…,v(t-59)，v(t-i)(i=0,1,…,59)均小于25 km/h，由于冲突方向上的两辆车进行过抢-让博弈，两车速度变化均具有波动性，车速时间序列可视作一个随机序列，通过建立ARMA模型进行速度预测.

图2 实车驾驶试验所获机动车1、2车速时间序列Fig.2 Vehicle 1 and vehicle 2 speed time Series acquired by real car driving experiment

4.2 预测建模

根据试验现场观察，车辆在进入交叉口后20 s内必驶抵冲突点，故需利用车速时序v(t-i)(i=0,1,…,59)建立ARMA预测模型，来描述t时刻之后20 s内车速变化情况，同样按1 s间隔进行车速更新，即实现v(t+j)(j=1,2,…,20)数值预测.

针对可能出现的建模数据适用性问题，采取如下方法进行判定：将观测车速序列分割为v(t-i)(i=20,21,…,59)和v(t-i)(i=0,1,…,19)两个子序列，将v(t-i)(i=20,21,…,59)作为观测值建立ARMA模型预测出v′(t-i)(i=0,1,…,19)，对比分析实际序列v(t-i)(i=0,1,…,19)与v′(t-i)(i=0,1,…,19)之间的差异，判定总序列v(t-i)(i=0,1,…,59)是否可用（样本数量N=40适用时，N=60必符合要求）.

4.2.1 基于部分车速时序的ARMA建模

取图2所示机动车1车速时序中的v1(t-i)(i=20,21,…,59)，机动车2车速时序中的v2(t-i)(i=20,21,…,59)，经周期差分、微分、取对数等运算后得到两车各自车速时序中，前40个数据之间自相关函数、偏相关函数值分布情况如图3所示.

图3 机动车1、2车速时序前40个数据间自、偏相关函数值分布Fig.3 Auto-correlation and partial-correlation function values of vehicle1 and vehicle 2 speed time series

从图3(a)和图3(c)中可看出机动车1、机动车2车速时序内前40个数据的自相关函数值分布具有“拖尾”性(q=0)；从图3(b)和图3(d)中可看出两车偏相关函数值分布具有明显的“截尾”性，其中机动车1函数值截尾处横坐标值为12(p=12)，机动车2截尾处横坐标值为11(p=11).因此，由前40个车速值构成机动车1、2车速子序列符合AR建模数据相关性要求(p≠0，q=0).利用matlab软件编制最小二乘估计程序，求得两车车速AR预测模型参数φ1i(1≤i≤12)、φ2i(1≤i≤11)，代入式(4)得到两车车速预测模型解析式为

以机动车1车速AR模型阐述其预测流程：将试验数据v1(t-i)(i=20,21,…,32)作为X1(t-j)(j=0,1,…,12)代入求解ε1(t)；假定ε1在下一时刻t+1不变，依次作替代操作X1(t)→X1(t-1),X1(t-1)→X1(t-2),…,X1(t-11)→X1(t-12)；求解得到X1(t)新值即为预测所得机动车1车速时序中第41个数据，即v1′(t-19)；根据X1(t-j)(j=0,1,…,12)新值重新计算求解ε1(t)并更新；重复上述步骤依次得到机动车1车速时序中第42,43,…,60个数据.根据上述模型及预测流程得到机动车1、2的预测车速及其与试验实测车速的对比分别如图4、图5所示.

对比图4、图5内曲线差异程度可看出，利用试验所获取的车速时序中前40个数据建立的预测模型对后20个车速的预测效果较好，计算两车预测车速归一化平均绝对误差(normalized mean absolute error,NMAE)，得到NMAE1=0.006 56，NMAE2=0.003 4，表明模型基本能反映车辆实际速度变化规律.计算机预测结果残差{ε(t)}自相关函数值如表1所示，所有值均小于，表明所建预测模型适用.

图4 机动车1预测值与实测值对比Fig.4 Comparison of vehicle1 predicted speed to actual speed

图5 机动车2预测值与实测值对比Fig.5 Comparison of vehicle 2 predicted speed to actual speed

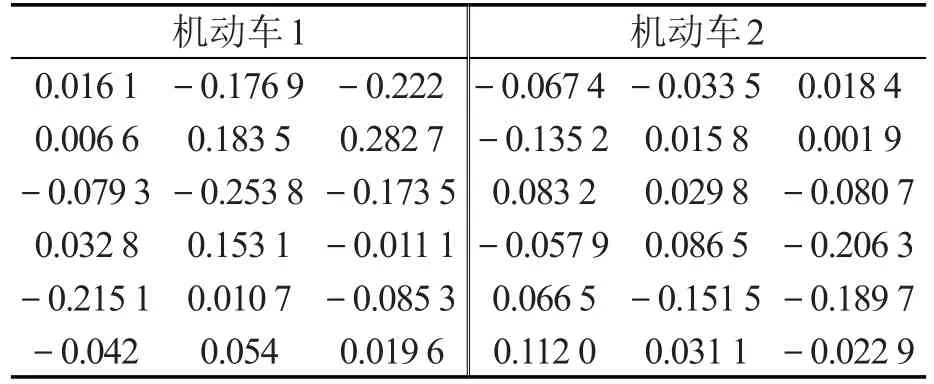
表1 机动车1、2预测结果残差自相关函数值Table 1Predicted speed of vehicle 1 and vehicle 2 residual errors auto-correlation function values

4.2.2 基于完整车速时序的ARMA建模

利用图2所示机动车1、2完整车速时序(60个数据)建立车速ARMA预测模型.通过计算其自相关函数、偏相关函数值，分析其数值分布曲线特征发现：两车自相关函数值、偏相关函数值分布均具有“截尾性”，其中机动车1p1=9,q1=9；机动车2 p2=5,q2=5.同样利用matlab软件求得两车车速ARMA预测模型参数φ1i(1≤i≤9)、θ1i(1≤i≤9)、φ2j(1≤j≤5)、θ2j(1≤j≤5)，代入式(4)得到两车车速预测模型解析式如下

对建立的ARMA预测模型进行残差{ε(t)}自相关函数检验，发现绝对值均小于，表明所建模型适用.利用上述模型分别预测两车在t时刻后20秒内车速值（每秒预测1次，共计20次），获得机动车1、2进入交叉口区域后车速值分布情况分别如图6、图7所示.其中，机动车2在t时刻后第8秒时的车速预测值为负值(-1.016 1km/h)，后续车速预测值亦在零值以下，考虑到车辆在交叉口内不会作重复性“停车-启动”动作，因此将预测所得负值及其后续车速预测值均以零值替代（如图7所示）.转化至实际驾驶场景中，可认为机动车2为避免碰撞而采取的紧急停车措施.

图6 机动车1车速预测值Fig.6 Predicted speed of vehicle 1

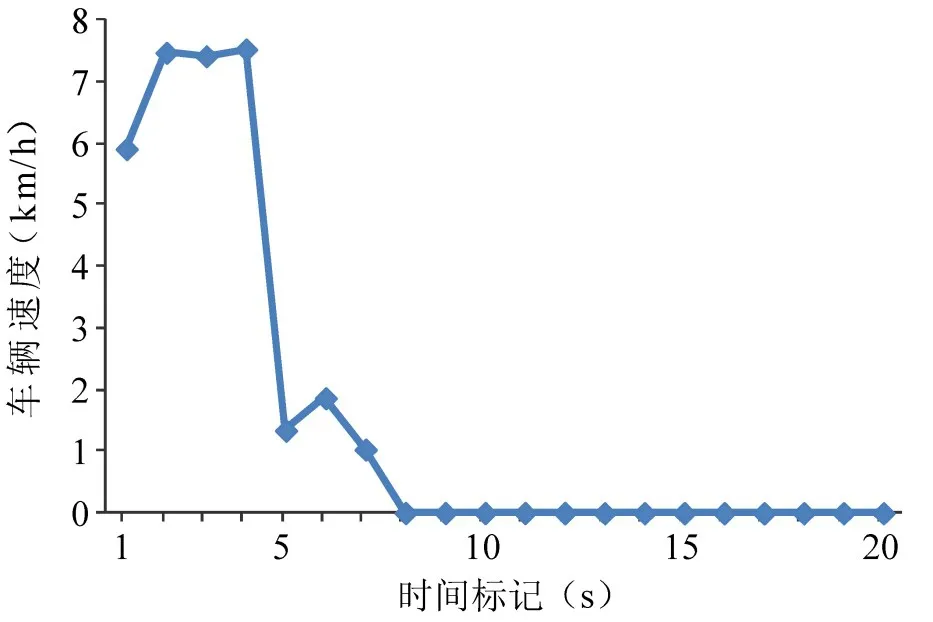
图7 机动车2车速预测值Fig.7 Predicted speed of vehicle 2

4.3 车速分析与碰撞风险评估

观察预测车速值分布情况可知，进入交叉口区域后，机动车1速度绝对值小(低于5 km/h)，加减速幅度小，表明机动车1行驶状态总体平稳，安全性高；而机动车2经历了“小幅加速-急剧减速”过程，车速起伏大，表明机动车2行驶状态较为冒进.对比机动车1、2进入交叉口区域前的车速分布情况(如图2所示)，从直观角度难以判断两车行驶状态为何种类型.而预测所得车速时序分布，能较好地反映两车最新的行驶状态.

若未采取制动措施，机动车2将率先抵达碰撞点.根据图7所示数据，利用式(1)可得机动车2最终停车位置距离碰撞点29.62 m，小于试验记录距离32 m，表明机动车2在抵达碰撞点前停车让行，假设机动车2停车位置恰好处于碰撞点，即式(1)中l1=29.62 m，k=8；将k值代入式(2)并结合图6所示数据、试验记录数据l2=30 m，可得s=24.69 m，考虑车体外形体积，实际距离约为2.16 m.从驾驶安全角度可知两车距离过小，发生碰撞事故风险较大.

5 研究结论

本文所提基于自回归滑动平均(ARMA)预测模型的交叉口车辆碰撞风险评估方法，旨在分析车辆进入交叉口前车速时序数据特征，推测车辆进入交叉口后车速时序数据，利用预测所得车速值计算车辆行驶位移及车间距离，作为判断交叉口内冲突方向车辆发生碰撞风险的依据.以零均值随机序列作为研究对象的ARMA模型，将不确定性影响因素以高斯白噪声形式融入其解析式中，通过模型参数φi(1≤i≤p)和θj(1≤j≤q)调整输出，故能较好地反映出车辆在进入交叉口前车速值分布及其变化特征，亦有利于准确预测车辆进入交叉口区域后的车速分布情况.

用以建模的车速时序数据源自实车驾驶试验.为保障安全，试验车辆未驶入交叉口内与另一方向车辆发生冲突、碰撞.本文利用试验采集所得车速时序中的前40个数据建立ARMA模型并预测后续20个数据值，与实测的20个车速值比对后发现：车速预测值准确度较高.由此推知，使用全部60个观测数据建立的车速预测模型更为准确.结合车速预测结果，对冲突方向上的两车速度进行了分析，通过推算其速度-位移-位置等变量演化过程，评估了两车所具有的碰撞风险.

本次研究不足之处在于：未考虑车辆应急反应而引起的车体横向偏移运动.因此，车辆碰撞点未必处于两车纵向正常行驶方向上；车辆进入交叉口之后加减速驾驶行为特征相比之前会变化并非完全延续.上述问题均与后续交叉口内车辆碰撞风险评估过程直接关联，应考虑使用更加符合驾驶人行为特征的车辆运行轨迹模型推演碰撞发生过程.另外，本次车速预测建模及其参数整定是在离线条件下进行.为增强模型普适性，应考虑引入ARMA建模参数自整定方法及其实现算法，协助预测模型自适应调整参数以应对驾驶环境变化.以上工作将在后续研究中开展.

[1]王鹏英,陆键,项乔君.公路平面交叉口交通冲突指标研究[J].公路,2008,(12):128-130.[WANG P Y,LU J, XIANG Q J.Research on traffic conflict index of highway intersection[J].Highway,2008,(12):128-130.]

[2]Spek A C E,Wieringa P A,Janssen W H.Intersection approachspeedandaccidentprobability[J]. Transportation Research Part F:Traffic Psychology and Behaviour,2006,9(2):155-171.

[3]Sun J,Sheng D,Xue B,et al.Comparative study of the impacts of red light cameras in China[J].Transportation Research Record,2012,2317:68-75.

[4]郭伟,杨明,王冰,等.基于博弈论的路口多车协作算法[J].华中科技大学学报(自然科学版),2011,39(增刊II):385-387.[GUO W,YANG M,WANG B,et al. Game theory based cooperative driving algorithm for intersection[J].JournalofHuazhongUniversityof Science and Technology(Natural Science Edition), 2011,39(Sup.II):385-387.]

[5]杨叔子,吴雅,轩建平,等.时间序列分析的工程应用(第二版)[M].武汉:华中科技大学出版社,2007. [YANG S Z,WU Y,XUAN J P,et al.Time series analysis in engineering application(Second edition)[M]. Wuhan:HuazhongUniversityofScienceand Technology Press,2007.]

[6]宗二凯,邵长桥.信号交叉口直右共用车道通行能力研究[J].交通运输系统工程与信息，2011,11 (6):62-67.[ZONGEK,SHAOCQ.Capacity researchonsharedthrough-rightturnlanesat signalized intersections[J].Journal of Transportation Systems Engineering and Information Technology,2011, 11(6):62-67.]

[7]Toque C,Terraza V.Time series factorial models with uncertainty measures:Applications to ARMA processes and financial data[J].Communications in Statistics-Theory and Methods,2011,40(9):1533-1544.

Risk Estimation to Vehicles Collision at Intersection Based on ARMA Prediction Model

ZHANG Liang-li1,ZHU He1,WU Chao-zhong2，3,ZHENGAn-wen1
(1.School of Information Science and Engineering,Wuhan University of Science and Technology,Wuhan 430081,China; 2.Intelligent Transport Systems Research Center,Wuhan University of Technology,Wuhan 430063,China; 3.Engineering Research Center for Transportation Safety,Ministry of Education,Wuhan 430063,China)

Speed time series collected as vehicles approaching an intersection can be used to predict several speed values as they subsequently entering it.Then,traveling tracks and spacing distances of the conflict vehicles are calculated by the predicted speed values,and the collision risk of them can be estimated. Because the speed distribution of a vehicle approaching to an intersection closes to the characteristics of random sequences,auto-regressive moving average(ARMA)theory is introduced to model the vehicle speed prediction.The modeling process includes time series data correlation test,p-q orders determination,formula coefficient estimation and model adaptability test.Test result shows that the ARMA model built by the previous 40 data of the observed speed time series could predict 20 values which are closed to the 20 observed ones.The other evidences of that are the normalized mean absolute errors of the conflict vehicles, which respectively equaled to 0.006 56 and 0.003 4.Further,the model built by all the 60 data of the observed time series is necessarily more applicable to predict vehicle speed,just as all the result values of the residual auto-correlation function test are less than 0.258 2.

intelligent transportation;collision risk estimation;auto-regressive moving average(ARMA); intersection;vehicle speed prediction

1009-6744（2015）05-0239-07

U491.3

2015-04-03

2015-05-22录用日期：2015-06-02

国家自然科学基金(51308426，51105286)；湖北省教育厅科学研究计划项目(B2013234).

张良力(1981-)，男，湖北武汉人，副教授，博士. ＊

zhangliangli@wust.edu.cn