多部门协同的内河失控船应急处置决策方法

吴兵，严新平，汪洋，魏晓阳

（武汉理工大学智能交通系统研究中心，国家水运安全工程技术研究中心，武汉430063）

多部门协同的内河失控船应急处置决策方法

吴兵，严新平*，汪洋，魏晓阳

（武汉理工大学智能交通系统研究中心，国家水运安全工程技术研究中心，武汉430063）

提出了一种基于模糊推理和决策偏好的群决策方法，以实现内河失控船的安全和有效的应急处置.首先，通过历史统计数据和文献综述，获取了不同影响因素下的失控船应急处置方案，确定了处置方案的决策准则；其次，利用模糊推理的方法对影响因素进行了模糊化，建立了模糊推理规则库和模糊推理机，通过去模糊化获取了不同决策方案下的决策准则值；再次，考虑到多部门协同的决策者的不同偏好信息格式，本文提出了一种基于一致性分析的线性规划模型，用于整合区间效用值、直觉模糊数和区间乘法偏好关系等决策偏好格式，从而获取不同决策准则的权重并得到最优决策方案.最后，应用典型案例进行了验证.结果表明，该方法能够很好地实现内河失控船的应急处置.

水路运输；群决策；模糊推理；失控船；偏好决策

1 引言

失控船的安全管理与应急处置一直是海事管理机构重点关注的问题.与海上发生失控险情不同，内河水域船舶通航环境复杂，船舶发生失控险情后，如果处置措施不当，则可能造成事故的发生[1].根据江苏海事局历史统计数据，目前对于失控船的应急处置有四种方案：在拖轮协助下继续作业(A1)，冲滩或者在航道外侧锚泊(A2)，锚泊于就近的锚地(A3)，应急锚泊于航道(A4).因此失控船的应急处置实际上是一个决策问题.对于该决策问题，首先需要确定决策准则，和普通船舶类似，失控船的航行安全也会受到自然环境（准则一），交通环境（准则二）和安全管理（包括应急救助资源，准则三）[2-4]的影响，同时根据Generic ship的理论[5]，还受到船舶安全状态（准则四）的制约，这四个因素就构成了失控船应急决策的准则.从实际统计数据来看，这四个决策准则是细分为风、流、能见度[2-3,6]等10个影响因素的，如表1所示.本文提出用模糊推理的方法将这些影响因素整合到四个决策准则中.另外，由于失控船的应急处置中，失控船需要考虑自身的安全，过往船舶也需要考虑到自身的的安全，同时海事管理机构需要考虑整个水域的通航秩序，因此该决策问题是涉及到这三个部门协同的群决策问题.在这个决策过程中，由于各个部门对决策问题的了解程度不同，其决策的偏好信息也会有所不同.对于失控船来说，由于其对自身的船舶状况最为熟悉，在决策时更偏好使用效用值的信息；而对于过往船舶来说，对失控船舶的了解程度相对较少，在决策时会存在难以把握的一些因素，常常偏好采用具有隶属度和犹豫度的直觉模糊数；而海事管理机构需要统筹考虑各个决策方案对过往船舶和失控船舶的影响，偏好采用两两比较的直觉乘法关系.鉴于此情况，本文提出了基于一致性的线性规划模型来整合这些偏好的信息格式.

2 失控船应急决策问题描述

记X={x1,x2,…,xt}(t≥2)为应急决策方案，G={G1,G2,…,Gs}为应急决策准则，w=(w1,w2,…,ws)为决策准则对应的权重向量，其值越大，表示相对应的决策准则更为重要，且为决策矩阵，为第i个决策准则对应第j种方案下的值.由此可得第j个方案的评价值为Zj(w)，如式（1）所示.

第一个问题是获取决策矩阵.考虑到本决策问题涉及10个影响因素，如果以这些影响因素为决策准则的话，在时间紧迫的应急局面中难以实施，因此该问题需要转换为获取四个决策准则值的问题.

第二个问题是获取决策准则的权重.失控船的应急决策过程涉及到海事部门、失控船舶和过往船舶等三类主体，设为DM={} d1,d2,d3，各个部门的偏好格式分别如下：

（1）区间效用值（失控船舶）.

（2）直觉模糊数（过往船舶）.

（3）区间乘法偏好关系（海事部门）.

该方法来源于经典的层次分析法，通过两两比较各个准则的重要程度来确定各个准则的权重，即可获得乘法偏好关系，可表示为其中~bij表示决策者认为Gi准则相对于Gj准则的重要程度.考虑到决策过程中决策者对于偏好关系也会采用区间形式，区间乘法偏好关系需要满足式(3).

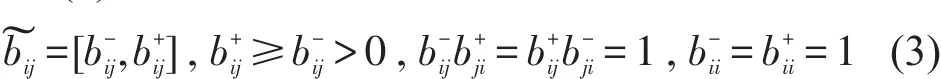
3 失控船应急决策模型

3.1 失控船应急决策框架

如图1所示，本文采集了不同决策方案的各个影响因素，在此基础上利用模糊推理，将影响因素整合到相应的自然环境、交通环境、船舶状况和应急救助资源四个决策准则中.同时考虑到专家决策时会对不同的决策方案有不同的偏好格式，因此提出一种基于一致性分析的线性规划模型.将区间效用值，区间直觉模糊数，区间乘法偏好关系这三种偏好格式进行整合，获取各准则的权重向量.最后利用式(1)进行最优处置方案决策.

图1 失控船应急处置决策框架Fig.1 Decision framework for disposal of NUC ships

3.2 基于模糊推理的决策准则值的获取

模糊推理在海事安全方面具有广泛的应用[2]，它主要包括模糊化、模糊规则库、模糊推理机和去模糊化四个部分.在本文中，首先利用隶属度函数对各影响因素和决策准则进行模糊化，从而转化成具有模糊特征的语言变量；然后建立模糊推理规则库，通过推理机实现影响因素与决策准则之间的关联；最后对获得的输出变量进行去模糊化，获取各决策准则的属性值.

3.2.1 模糊化输入和输出变量

模糊化各个变量时目前主要采用隶属度函数的方法，由于三角形隶属度函数非常直观，因此应用最为广泛[2,7].每个隶属度函数可表示为qe=(q1,q2,q3)，根据江苏海事局2009-2012年间发生的失控船统计数据，本文采用累积频率的方法获取隶属度函数.图2为一标准的三角隶属度函数，对于语言变量“EF”，其q1的值为累积频率25%对应的变量值，而q2和q3则分别为50%和75%.类似地，通过采用该方法可以获取各影响因素的模糊化数值，如表1所示（A3为例）.需要指出的是，表1的前6个变量在不同的决策方案下其参数存在差异，而后4个变量则相同.各输出变量（决策准则）统一采用如图2所示的三角模糊隶属度.

图2 标准三角形隶属度函数Fig.2 Standard triangular membership function

3.2.2 建立模糊推理规则库

模糊化输入和输出变量之后，需要建立模糊推理机，本文采用Mamdani推理方法，该方法的原理如式（4）所示，式中的μAl(xm)为语言变量xm的mk隶属度.各个决策准则的模糊推理机如图3所示，需要注意的是（d），该推理机A1方案只有一个输入变量，而A2、A3和A4则增加了两个输入变量，这是由于决策时会对这三个输入变量进行优先级排序，从而影响其决策规则，具体在决策规则库中进行设置.

表1 模糊化各输入变量（A3为例）Table 1Fuzzified input variables(A3 case)

图3 决策准则模糊推理机Fig.3 Fuzzy inference engine for decision attributes

模糊推理的另一个重要组成部分是模糊推理规则库，常用的格式为IF-THEN规则.如式（5）所示.

式中Almk(i=1,2,…,M)和Blk分别是输入变量和输出变量的模糊集；xk=(x1k,x2k,…,xnk)T∈U和y∈V分别为输入和输出变量的语言变量.同时令L是第k个决策准则的模糊规则(l=1,2,…,L).根据该IFTHEN推理规则，建立A3的决策推理规则如表2所示（以救助资源为例）.

3.2.3 决策准则去模糊化

获取模糊输出语言变量之后，利用式（6）所示的重心法对其进行去模糊化，获得不同决策方案下的决策准则的值.

表2 救助资源模糊推理规则库（A3为例）Table 2Fuzzy rule base for rescue resources(A3 case)

3.3 多种偏好信息下的目标规划模型

3.3.1 区间效用值

假定所有的权重向量都包含于区间效用值中，则认为这个区间效用值是一致性的.

但是这在大多数情况下是难以实现的，因此徐泽水[8]提出利用一致性来确定区间效用值的权重.并引用了正偏差向量和负偏差向量来进行描述.

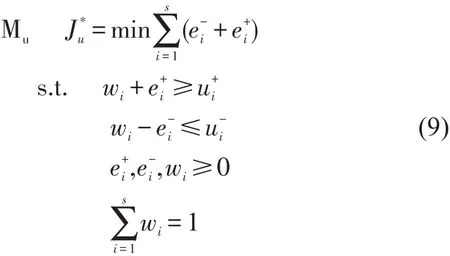
3.3.2 直觉模糊数

直觉模糊数和区间模糊数有一定的差异，但是可以通过文献[9]提供的方法将直觉模糊数转换为区间模糊数.具体过程为：直觉模糊数可以转换为，对于一个具有一致性关系的直觉模糊数来说，需要满足式（10）.

和区间效用值类似[8]，通过引用正负偏差向量和，可以建立以正负偏差向量之和最小为目标函数的线性规划模型Mp.

3.3.3 区间乘法偏好关系

对于具有一致性的区间乘法偏好关系，需要满足式（12）的条件.

类似地[9]，引用正负偏差向量c-ij和c+ij，可以建立以正负偏差向量之和最小为目标函数的线性规划模型Mm.

3.3.4 整体目标规划模型

由式（1）可知，Zj(w)值最大的方案即为最优方案，而通过前面建立的Mu、Mp和Mm模型，可以建立本决策过程的多目标最优模型如下：

又由于

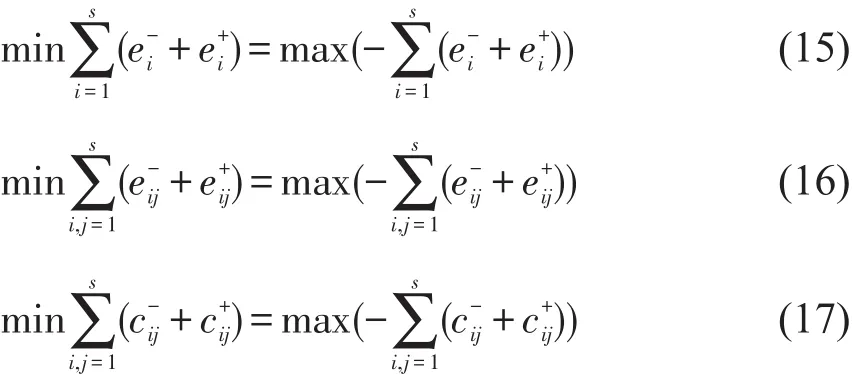
则可以获得最优线性规划模型为

求解该线性规划模型，即可获得最优的失控船应急处置决策方案.

4失控船应急实证研究

4.1 失控船应急决策情景

2009年9月份，一艘船长为98 m的干货船在长江下游航段41#黑浮附近发生了主机失控险情，当时能见度约为5 000 m，东北风4-5级，船舶距离最近的张家港危险品锚地约0.8海里，航道外侧水域水深条件良好，可以满足该船舶临时锚泊的需要，利用该航道外侧成功应急锚泊的概率为0.7左右；险情离张家港港区较近，应急拖轮约20-25分钟可以到达，距离码头水域约2海里.尽管该处水域位于福南水道、福中水道和福北水道汇流处，此时船舶流量一般，约每小时18艘左右.

4.2 获取决策矩阵

首先将上述的各个影响因素数值分别进行模糊化，可以获取在不同决策方案（A1，A2，A3，A4）下的语言变量，再根据图3所示的Mamdani型模糊推理机，按照建立的IF-THEN模糊推理规则库，获取输出变量的语言变量，然后根据公式（6）所示的重心法将语言变量进行去模糊化，可获得不同决策方案各个决策准则的值，如表3所示.

表3 不同决策方案下的决策准则值Table 3Attribute values of different alternatives

从表3准则值可以看出，A1方案虽然没有某个准则的得分值最高，但是相对较为平均；而A2方案因为航道外侧能够利用的概率较高，在救助资源方面得分值最高；A3方案则在交通环境方面得分最高；A4方案由于采用紧急抛锚方案，受自然环境影响较小，其在自然环境的得分最高.由于这些方案在各个方面均有自身的优势，因此需要获取各个决策准则的权重向量，得出最优方案.

4.3 专家评价权重

在进行该决策时，分别选取了一名海事管理人员，两名高级船员（分别代表失控船舶和过往船舶）对本案例进行评价.过往船舶的决策信息是以直觉模糊数的形式给出，其值为

该直觉模糊数可以转换为区间模糊数.

其他两个决策者的信息也分别给出为

根据建立的线性规划模型Mf可以获得权重向量和偏差变量的值.

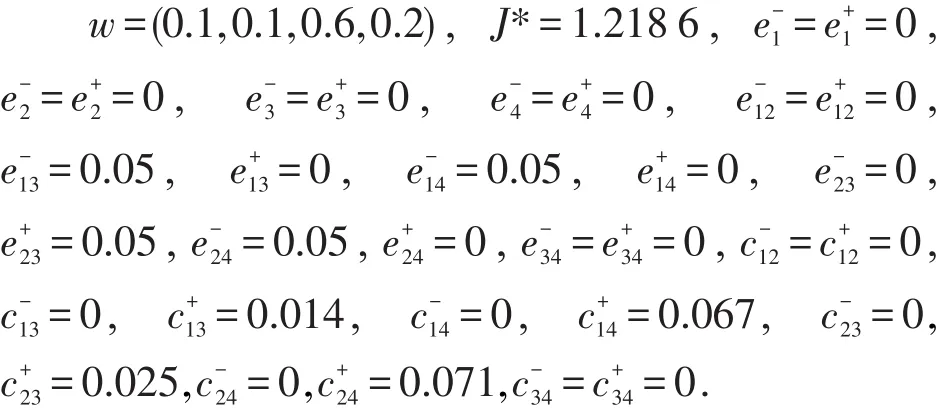
由以上的偏差变量的值可以看出，所有的偏差向量均大于且接近于0，因此具有很好的一致性，该条件下的结果即为最优的决策方案.

4.4 最优决策方案

在上述决策变量条件下，可以求得：

而根据定义，易得到各决策方案的综合评价结果，分别为

因此可以获得各个决策方案的排序为A3＞A1＞A2＞A4

因此，方案A3为最优方案，该方案与实际处置时采用的方案一致，即锚泊于张家港危险品锚地.

5 研究结论

本文提出了一种基于模糊推理和偏好决策的内河失控船应急处置方法.考虑到应急处置时时间紧迫，因此采用历史统计数据和模糊推理结合的方法，可以快速地获得具有典型特征的决策准则属性值.需要指出的是，本文的应急决策方案是基于江苏海事局的历史统计数据，在应用于长江中上游水域时可能还需要进行适当的调整；另一方面，由于数据采集的难度等客观因素，历史统计数据并不一定能涵盖所有的影响因素.因此对于失控船应急处置的影响因素还可以进行更为深入地研究.而对于各个评价准则的权重，考虑到时间紧迫性和多部门专家对于实际应急情景的了解程度，群决策中各个决策者对于不同的评价信息格式有不同的偏好，本文应用的基于一致性的线性规划方法可以很好地整合区间效用值、直觉模糊数和区间乘法偏好关系等数据格式.研究结果表明，该方法具有很好的实用性和可靠性.此外，尽管在实际过程中各个部门可能不会严格按照这种偏好格式进行决策，但是通过该目标规划模型可以对这三种偏好格式的任意组合进行整合，因此该方法具有较强的推广性.

[1]甘浪雄,喻晓,高国章.船舶失控应急的港珠澳大桥桥区水域尺度[J].中国航海,2012,34(4):76-80.[GAN L X,YU X,GAO G Z.Range of bridge water area of Hong Kong-Zhuhai-Macao Bridge for out-of control ships in emergency[J].Navigation of China,2012,34(4):76-80.]

[2]吴兵,严新平,汪洋,等.基于桥梁通航风险的海巡艇配备研究[J].中国航海,2013,36(4):82-85.[WU B, YAN X P,WANG Y,et al.Maritime patrol resource configurationbasedonnavigational risks in bridge area[J].Navigation of China,2013,36(4):82-85.]

[3]Wu B,Wang Y,Zhang J,et al.Effectiveness of maritime safety control in different navigation zones using a spatial sequential DEA model:Yangtze River case[J]. Accident Analysis&Prevention,2015,81:232-242.

[4]Zhang D,Yan X P,Yang Z L,et al.Incorporation of formal safety assessment and Bayesian network in navigational risk estimation of the Yangtze River[J]. Reliability Engineering&System Safety,2013,118:93-105.

[5]Lois P,Wang J,Wall A,et al.Formal safety assessment of cruise ships[J].Tourism Management,2004,25(1): 93-109.

[6]Zhang J,Yan X,Zhang D,et al.Safety management performanceassessmentforMaritimeSafety Administration(MSA)by using generalized belief rule base methodology[J].Safety Science,2014,63:157-167.

[7]杜珺,王瑞红.基于三角模糊数的锂电池航空运输火灾事故树分析[J].交通信息与安全,2014,32(3):119-122.[DU J,WANG R H.Fire risk of Lithium-ion Batteries in air transportation based on fault tree method and tri-fuzzy theory[J].JournalofTransportation Information and Safety,2014,32(3):119-122.]

[8]Xu Z.Multiple-attribute group decision making with differentformatsofpreferenceinformationon attributes[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2007,37(6):1500-1511.

[9]Xu Z S,Chen J.MAGDM linear-programming models with distinct uncertain preference structures[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B: Cybernetics,2008,38(5):1356-1370.

A Modified Decision-making Method with Multidivisional Cooperation for Disposal of NUC Ships

WU Bing，YAN Xin-ping，WANGYang，WEI Xiao-yang
(National Engineering Research Center for Water Transport Safety(WTSC),Intelligent Transportation System Research Center, Wuhan University of Technology,Wuhan 430063,China)

In order to dispose the not under command(NUC)ships effectively and safely in inland waterway transportation,a modified group decision making methodology is proposed based on fuzzy rule reasoning and decision preference.First,according to the statistical data and literature review,the influencing factors of emergency disposal options is obtained,and the decision attribute is also defined.Second,the fuzzy reasoning is introduced to integrate the influencing factors;moreover,after establishment of the fuzzy rule base and fuzzy inference engine,the linguistic variables of decision criteria with respect to the alternatives are defuzzified into crisp values.Third,considering the decision-maker may prefer different formats of information,a consistency-based linear programming method is proposed to integrate the information,including interval utility value,intuitionistic fuzzy numbers and interval multiplicative preference relation.The weights of attributes and the best alternative,then,can be obtained.Finally,a typical illustrative example is used to verify the proposed approach,and the result represents that this model is useful and beneficial for disposal of NUC ships.

waterway transportation;group decision-making;fuzzy reasoning;NUC ships;decision preference

1009-6744（2015）05-0016-08

U698.6

A

2015-04-01

2015-06-11录用日期：2015-06-18

国家科技支撑计划（2015BAG20B05）；高等学校博士学科点专项科研基金(20130143120014).

吴兵（1986-），男，江西芦溪人，博士生. ＊

xpyan@whut.edu.cn