多分量调频信号源混合相交非正交联合对角化盲分离

李纪永，李舜酩，田国成，陈晓红，王 勇

(1.南京航空航天大学能源与动力学院，江苏南京210016；2.山东中实易通集团有限公司，山东济南250000；3.南京航空航天大学理学院，江苏南京210016)

多分量调频信号源混合相交非正交联合对角化盲分离

李纪永1，李舜酩1，田国成2，陈晓红3，王 勇1

(1.南京航空航天大学能源与动力学院，江苏南京210016；2.山东中实易通集团有限公司，山东济南250000；3.南京航空航天大学理学院，江苏南京210016)

针对多分量调频信号源混合相交时频分布盲分离，提出白化-均匀加权非正交联合对角化(Whitening-Uniformly Weighted Exhaustive Diagonalization using Gauss iteration，简称W-UWEDGE)方法估计混合矩阵。白化对相关信号去冗余处理，无需约束源信号概率密度形式，仅限制源之间整个时频面上无完全重合成分，非正交联合对角化则针对复数域。首先将非正交联合对角化可辨识性从时延平面推广至二次型时频平面，然后利用基于白化处理的梯度范数选择自项时频点(auto-time frequency point)，进而利用均匀加权近似联合对角化方法估计混合矩阵，分析Amari error值随信噪比及时频矩阵个数的变化规律，与针对混合信号时间历程及时频分布的两类分离方法进行性能比较，显示出所提盲分离方法的优越性。最后应用于转子运行状态识别与齿轮复合故障源分离。仿真与实验数据分析表明所提出方法分离多分量调频相关源的有效性。

多分量调频信号；二次型时频分布；白化；非正交联合对角化；盲源分离

引 言

盲源分离中，ICA(Independent Component A-nalysis)通常假设源信号之间统计独立，且对于相互独立的高斯信号，经过正交变换仍然为高斯信号，不能得到正确分离。联合对角化将这一假设条件放宽至源信号之间互不相关，更符合实际应用情况。对角化矩阵有时延协方差矩阵、累积量切片矩阵［1］、不同时间窗下源协方差矩阵，或其他反映源统计或结构特性的矩阵等［2］。不同源信号时延协方差考虑了与之相关的临近点上的信息，即利用了时序特性，有足够的额外信息对非平稳信号进行盲分离，而基于高阶统计量的ICA出现过学习问题，即原本属于一个时序上的信号，被分离成两个不相关的信号，故应用时序特性对非平稳信号进行盲分离具有优势。

联合对角化按照对角化矩阵是否有正交(酉)性约束，分为正交联合对角化和非正交联合对角化(Nonorthogonal Joint Diagonalization，简称NOJD)。正交需要白化预处理，其概念明晰，在早期发展的联合对角化方法中应用较多［3］，但白化影响了分解性能，且对于非高斯分布的信号，白化效果较差，非正交联合对角化无需预白化处理，即无酉约束，随酉约束松动，需额外施加约束，文献［4］提到解混矩阵的每一列需满足单位欧几里得范数约束条件，QRJD方法约束零延迟自相关矩阵的变换为单位矩阵［5］，即约束源信号具有单位能量值，一般来讲，只有零延迟自相关矩阵为正数时，约束才有效，如果含噪，则对角化方法估计混合矩阵的精度下降。

双转子或三转子燃气轮机如航空发动机启动或关闭过程中，高、低压转子升降速时其运行状态时频分布呈相交特性，此时的轴承振动、齿轮振动，由于谐波随转速变化，则往往呈多分量时频相交分布形式，尤其是在机动飞行中，参数变化多，且呈时变非平稳特性，无论运行状态还是旋转部件的响应时频变化复杂，包含多种分量［6］；在复合故障中，如齿轮的磨损与断齿，轴承的滚动体、内外圈点蚀故障等局部故障，其间断碰摩的耦合振动信号时频分布往往呈多分量相交特性，每个冲击脉冲都可以看作一个线性调频信号，若运行状态如转速变化，则其时频分布更加复杂。

对于线性时频相交混合信号，文献［7］利用k均值模糊聚类将计算的空间矢量分类，然后估计混合矩阵。对于二次型时频分布，一个关键是自项时频点的选择，文献［8］设定比值阈值，计算各频率点时间切片时频分布与最大频率点时间切片比值，进而选择自项时频点，然后根据聚类方法进行空间矢量分布进而估计混合矩阵。文献［9］对混合信号时频分布进行特征值分解，计算各时频点矩阵特征值与其总特征值比值，然后计算梯度范数，综合得出自项时频点。多数文献都针对单分量调频信号源混合信号进行非正交联合对角化，对于多分量时频源混合相交［10］，混合时频分布更为复杂，其自项时频点的选择方法及非正交联合对角化方法值得进行进一步地研究。

本文对多分量调频源混合相交信号进行白化-非正交联合对角化，进而估计混合矩阵。利用预白化去除相关冗余成分，无需假设源信号概率密度形式，利用均匀加权分布非正交联合对角化方法估计分离矩阵，对时频矩阵进行范数约束，研究Amari error值随信噪比及时频矩阵个数变化特性。将方法应用于实测转子振动信号，成功识别出转子运行状态；应用于齿轮磨损与断齿复合故障中，分离出磨损与断齿的时频分布。

1 二次型时频矩阵非正交对角化可辨识性

含噪混合信号模型为

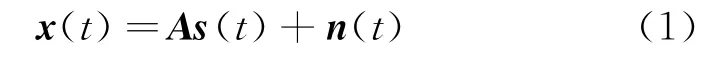
式中 x(t)=［x1(t)，…，xm(t)］T，表示m维观测信号；s(t)为n维源信号；A为m×n满秩混合矩阵，n(t)为独立同分布的噪声向量，与源信号相独立，即δ(τ)σ2Im，Im为单位矩阵，δ为Dirac函数，上标*代表共轭转置，σ2为信号方差，可通过奇异值分解进行求解。

通过辨识混合矩阵A进行盲分离时，混合矩阵估计存在幅值及顺序不确定性，即估计混合矩阵ˆA=ADP，D为非奇异n×n对角矩阵，P为n×n置换矩阵。

源信号协方差矩阵表示为

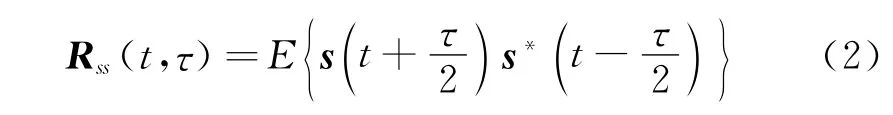
混合信号的协方差矩阵为

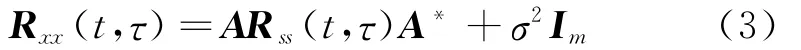
当源信号自相关函数形状互不相同的情况下可实现盲分离，即

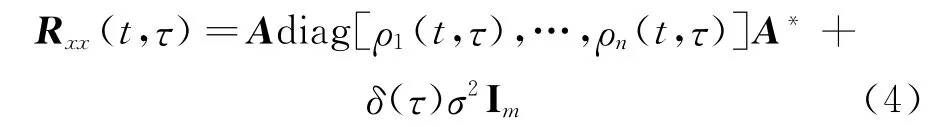
其演变谱(evolutive spectrum)为

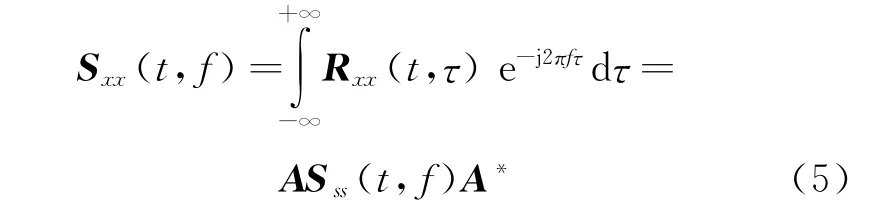
信号对称形式的双线性变换更能表现出非平稳信号的重要特性［1］。其Wigner-Ville谱为

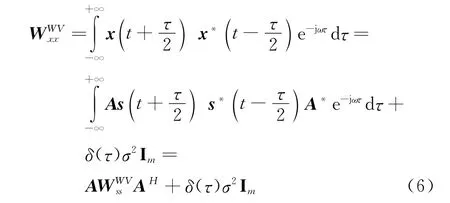
由式(5)，(6)可知，演变谱为Wigner-Ville谱的期望，即

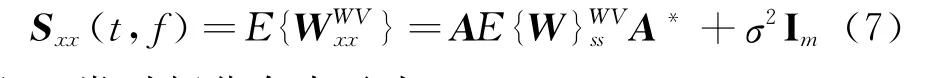
Cohen类时频分布表示为

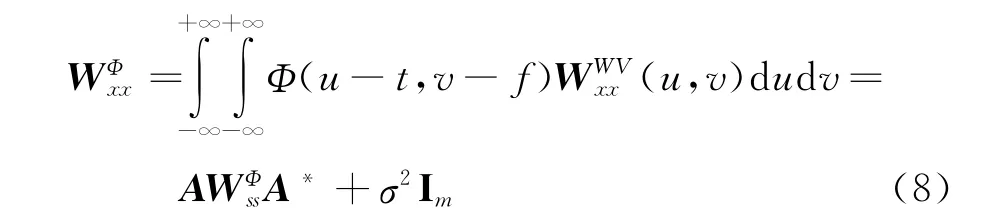
式(8)即将可辨识性从二维时延平面推广至二次型时频平面。

推广至更一般的情况，即混合信号的相关矩阵并不是对角矩阵，则可通过对角化混合信号的源自项时频点估计混合矩阵，即在观测信号的时频矩阵WΦxx(ti，fi)，i=1，…，k中选择若干个i点，在此处只含有一个源成分，然后对其进行对角化即可估计混合矩阵。

2 基于白化处理的自项时频点寻优

对时频相交混合信号进行PCA分解处理，进而得到一个n×m满秩白化矩阵D，使得D(AA*)·D*=In，令酉矩阵U=DA，对含噪信号的噪声子空间进行抑制，得到白化-噪声抑制后的时频分布矩阵

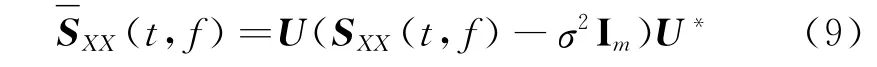
式(9)即为解相关之后的时频分布，满足零延迟时频矩阵对角分布，本文即从解相关时频分布里寻找自项时频点。

由式(7)和(9)可得到解相关之后的演变谱

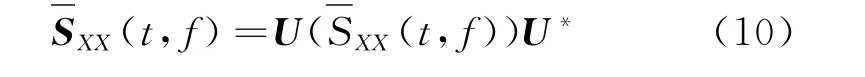
进而由式(8)可得

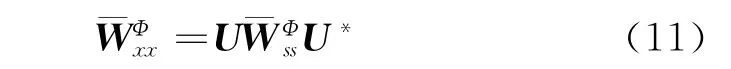
对白化后的时频分布进行奇异值分解，即可得到如下关系式

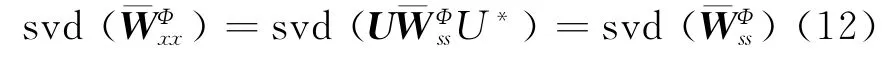
式中 ε为梯度阈值，用以调整局部极值点的个数。HC(t，f)＜0表示取极大值，满足此条件即得到源自项时频点。

3 基于均匀加权最小二乘准则估计混合矩阵

对于不含噪信号，估计混合矩阵的直接形式为

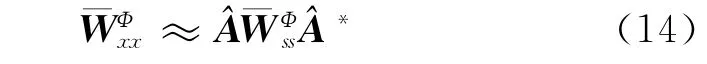
间接形式为

将直接及间接形式融合在一起，采取基于均匀加权最小二乘准则的最小化非对角元素方法，非对角元素其最小二乘表示如下

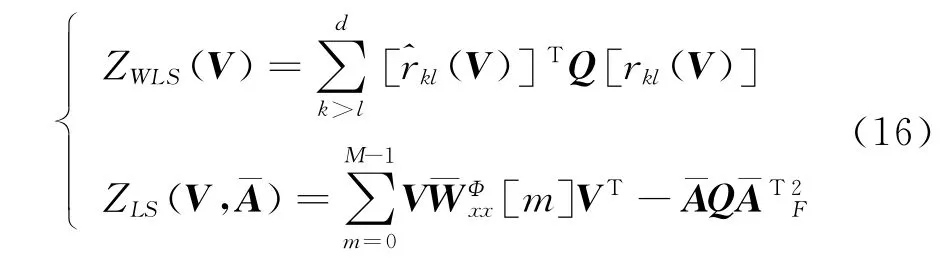
式(16)综合考虑了直接及间接求解解混矩阵的形式。T表示转置，V为解混矩阵，为残余混合矩阵，即对目标矩阵进行对角化后的残余矩阵，可表示为

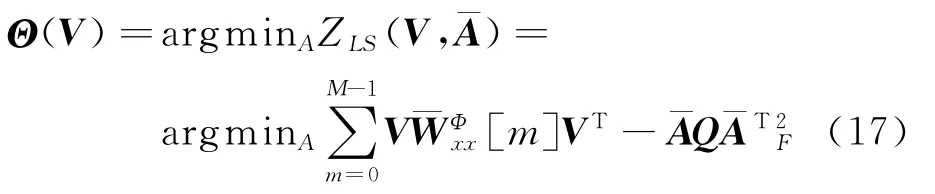
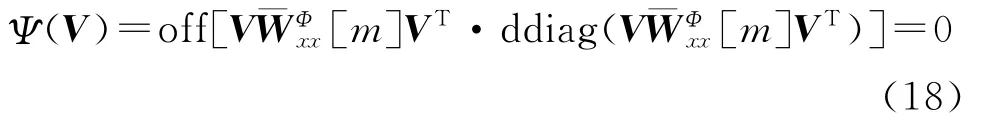
对于任何一组目标矩阵，满足条件(18)，式(17)即可得到收敛的解［2］。

针对多分量调频源混合信号，估计混合矩阵核心步骤为：

1)利用式(9)对多分量调频混合信号进行白化处理得到式(11)；

2)利用式(13)梯度范数对去相关信号进行自项时频点选择；

3)将步骤2)中的时频点位置对应至混合信号时频矩阵中，即得到源混合信号的自项时频点矩阵。

4)由式(17)对混合信号的自项时频点进行非正交联合对角化，估计混合矩阵。

4 时频相交仿真信号盲分离

构造多分量线性调频信号：

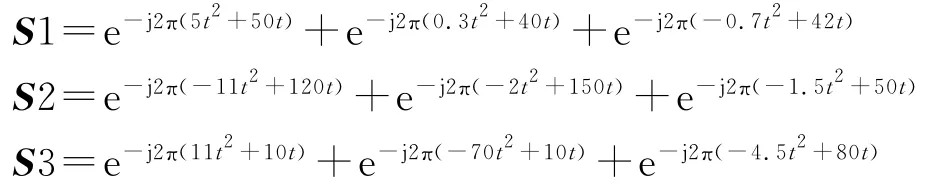
其中，采样频率为500 Hz，采样点数为512，t的范围是［0 1.024 s］。

源信号的时间历程及时频图如图1所示。

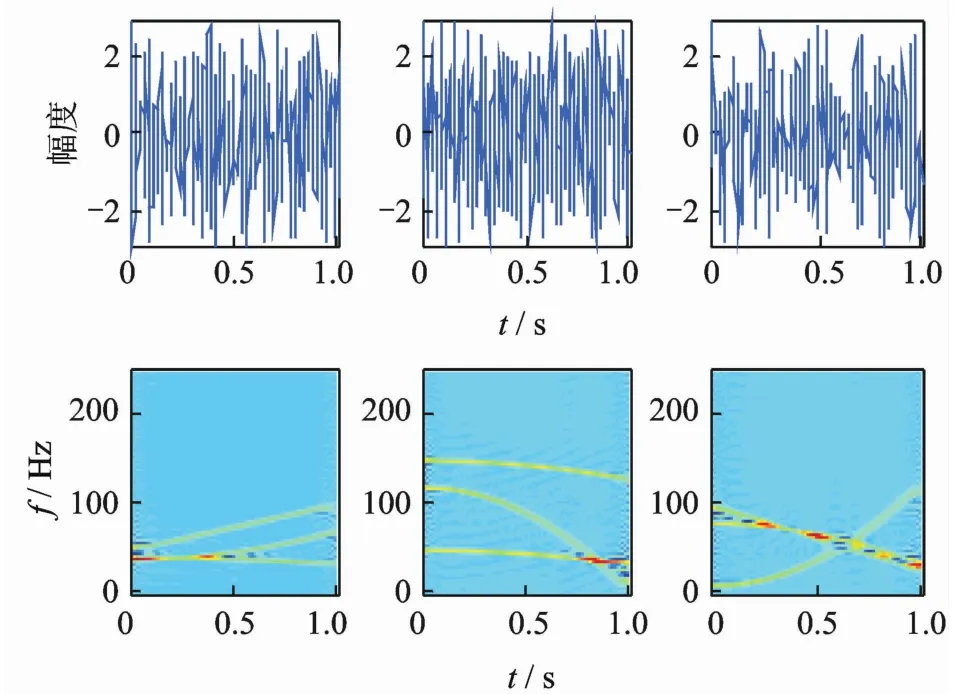
图1 源信号时间历程及时频分布Fig.1 Signal time history and TFdistribution

利用基于白化处理的梯度算法得到混合信号的自项时频点分布如图2所示。

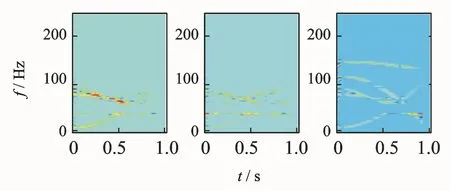
图2 自项时频点分布Fig.2 Autosource TFpoints distribution

对混合信号自项时频点进行均匀加权盲分离结果如图3所示，直观上与图1对比，可知采用 WUWEDGE取得了比较理想的结果，其amri error值为0.004 7，一般认为amri error值在10-3数量级时能达到较好分离效果。

图3 分离信号时频分布Fig.3 Demixed signal TFdistribution

图4为进行多次随机实验(即混合矩阵随机，本文多次即指100次左右)下所得Amari error平均值，随着信噪比减小，分离性能迅速下降，但在信噪比较大(本文约大于6)时能识别出源信号，故本文所提出的方法有明显的抗噪声干扰能力。

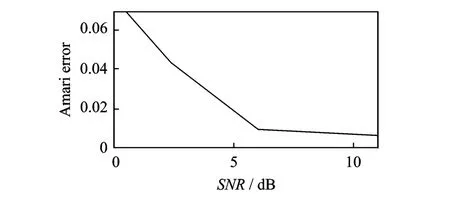
图4 Amari error平均值随信噪比变化Fig.4 Mean Amari error value under different SNR

图5为不同时频个数下Amari error平均值。可以看出，Amari error值并非与时频矩阵个数成线性比例，存在一个最佳个数，在本文中，利用基于白化处理的梯度范数计算方法选取了2 216个3×3时频矩阵，进行非正交联合对角化的最佳个数在1 200～1 300之间，这是由于在进行联合对角化时存在估计误差，而在实际应用中，不可避免地存在噪声的影响，可多次尝试去选取适当的时频矩阵个数进行盲分离，总体上看，随着个数增多，Amari errror值趋向平稳，能得到满意的分离效果。

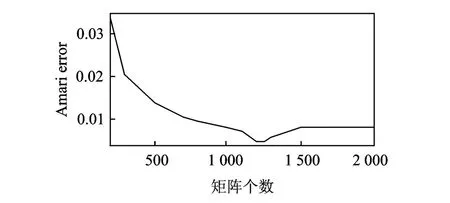
图5 Amari error值随矩阵个数变化Fig.5 Amari error value under different TFmatrix number

用不同方法对信号进行盲分离的效果比较如表1所示，所选取的对比方法分为两类，一类直接对混合信号进行分解，所采取的对比方法有SOBI(Second-order blind identification)，FASTICA，WASOBI(Weights Adjusted SOBI)［11］，BGSEP(Block Gaussian Separation)［2］，BARBI(Block-wise Stationary Autoregressive BI)［12］。这几种方法针对混合源信号进行盲分离，但都不是针对混合相关源信号，且对源信号概率密度亦有限制，分离效果如表1所示，并不能有效分离出相关源信号。另一类针对本文的二次型时频矩阵，选取了几个典型方法，包括LU分解LUJD，QR分解QRJD［5］，AC-DC［3］，非均匀加权WEDGE分解BGWEDGE［2］，通过对比可知，本文所提出白化-非正交联合对角化方法能比较好地分离出相关源信号。

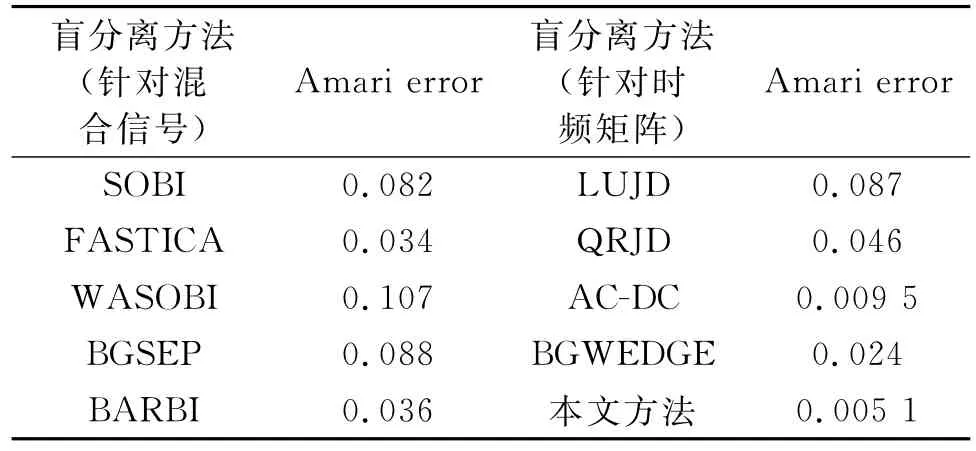
表1 多次随机实验计算的Amari error平均值Tab.1 Mean Ameri-erro valuae under a number of random numerical simulation

5 实验验证

5.1 转子运行状态识别

两转子共同固定在同一基座上，分别由电机驱动，如图6所示。其中1#进行加速运转，从大约480 r/min加速至720 r/min左右；2#进行转速呈正弦状态的运转，幅值在560 r/min至960 r/min间变化，布置两个互相垂直的涡流传感器监控1#转子及2#转子的位移变化，采样频率1 k Hz，截取10 s钟信号，所测得的混合信号时间历程如图7所示。

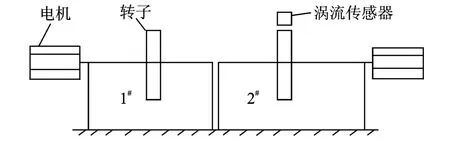
图6 转子实验装置Fig.6 Rotor experiment apparatus

混合信号时频分布如图8所示，两个源混合在一起，由于噪声及混合矩阵的影响，加速状态虽显示不明显，但仍可看出为时频相交混合信号。

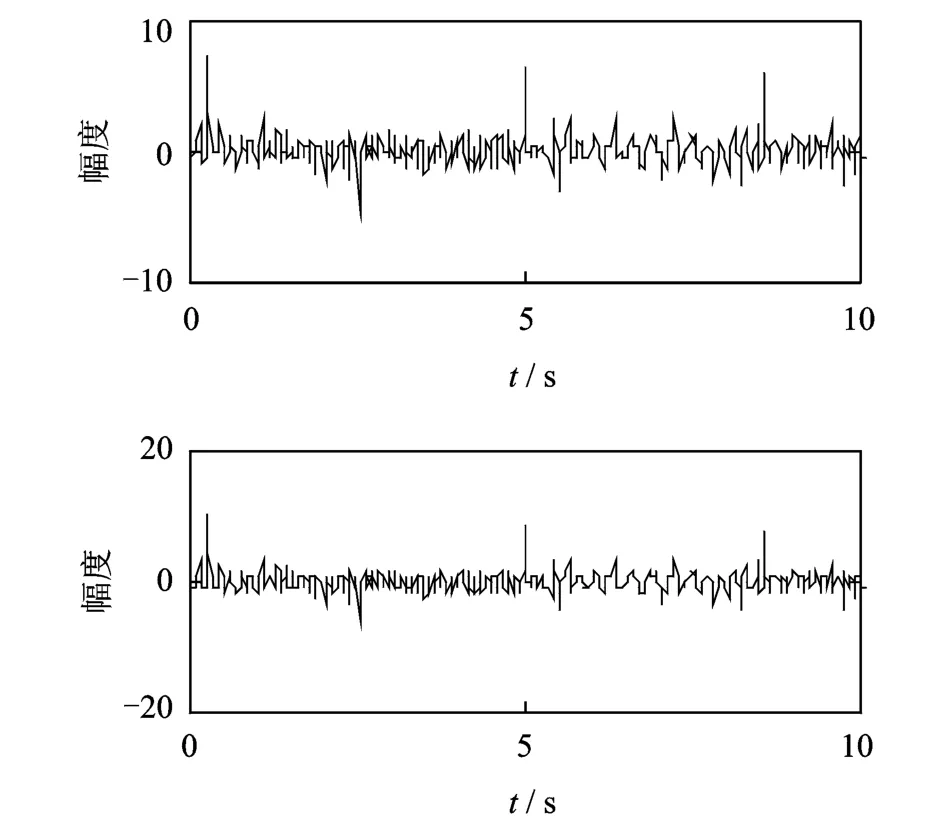
图7 混合信号位移时间历程Fig.7 Mixed signal displacement time history

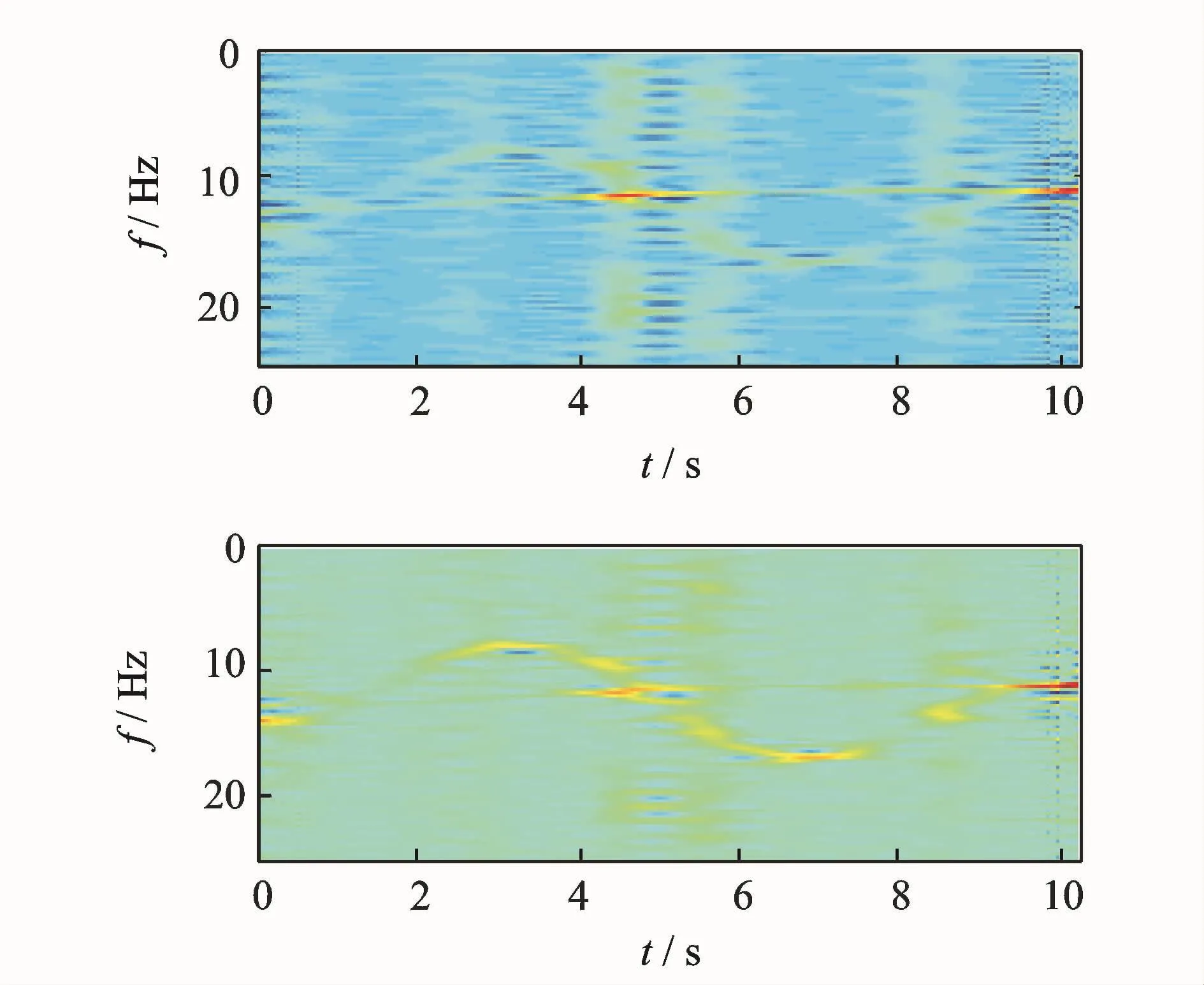
图8 混合信号时频分布图Fig.8 Mixed signal TFdistribution

对混合时频进行分离，即首先对传感器测得的混合信号进行白化预处理得到自项时频点位置，对所有选取的时频矩阵进行联合对角化估计混合矩阵，未降噪处理的混合振动信号盲分离结果如图9所示。

对混合信号进行降噪处理，进行源自项时频点选择，然后对源自项时频分布点进行非对角联合正交化盲分离，所得振源时频分布结果如图10所示，与未降噪时的图8相比，转子的运行状态能更明晰地反映出。从另一个方面讲，在不进行降噪情况下，能够大体看出来转子运行变化趋势，说明了方法具有一定的抗噪性。

图9 转子振源盲分离时频分布Fig.9 Rotor vibration TFdistribution

图10 降噪信号盲分离时频分布Fig.10 Denoised signal TFdistribution after BSS

5.2 齿轮复合故障振源分离

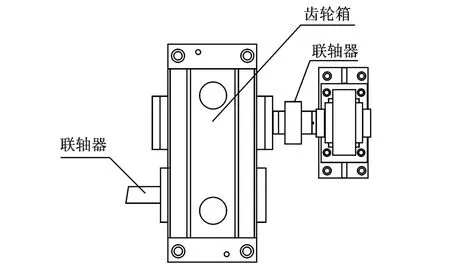
图11 齿轮箱示意图Fig.11 Schematic of gearbox

齿轮箱示意图如图11所示。运行过程中，转速在1 470 r/min上下轻微浮动约2 r/min，未施加负载，输入输出轴各有一个加速度传感器，所测方向相同。共有恒定转速下的大齿轮断齿故障、小齿轮磨损故障、大齿轮断齿-小齿轮磨损复合故障。

图12为大齿轮断齿-小齿轮磨损复合故障时频分布，由于冲击的影响，时频分布呈间断特性，冲击与引起的固有振动等分量混合在一起，无论是从能量分布还是从边频带分布都难以区分断齿和磨损故障，经过本文方法的分离，其结果如图12所示，从能量分布上进行判别，可知，与磨损相比断齿的冲击特性更明显，且较高频带40～100 Hz分量能量值不如磨损故障明显。这与相同运行状态下单故障源时频一致，限于篇幅，单一故障下齿轮振动信号时频图未给出。

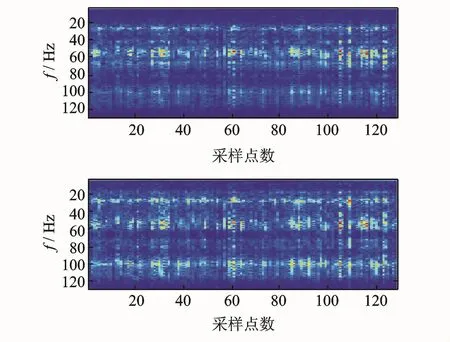
图12 复合故障齿轮信号时频分布Fig.12 Composite gear fault signal TFdistribution

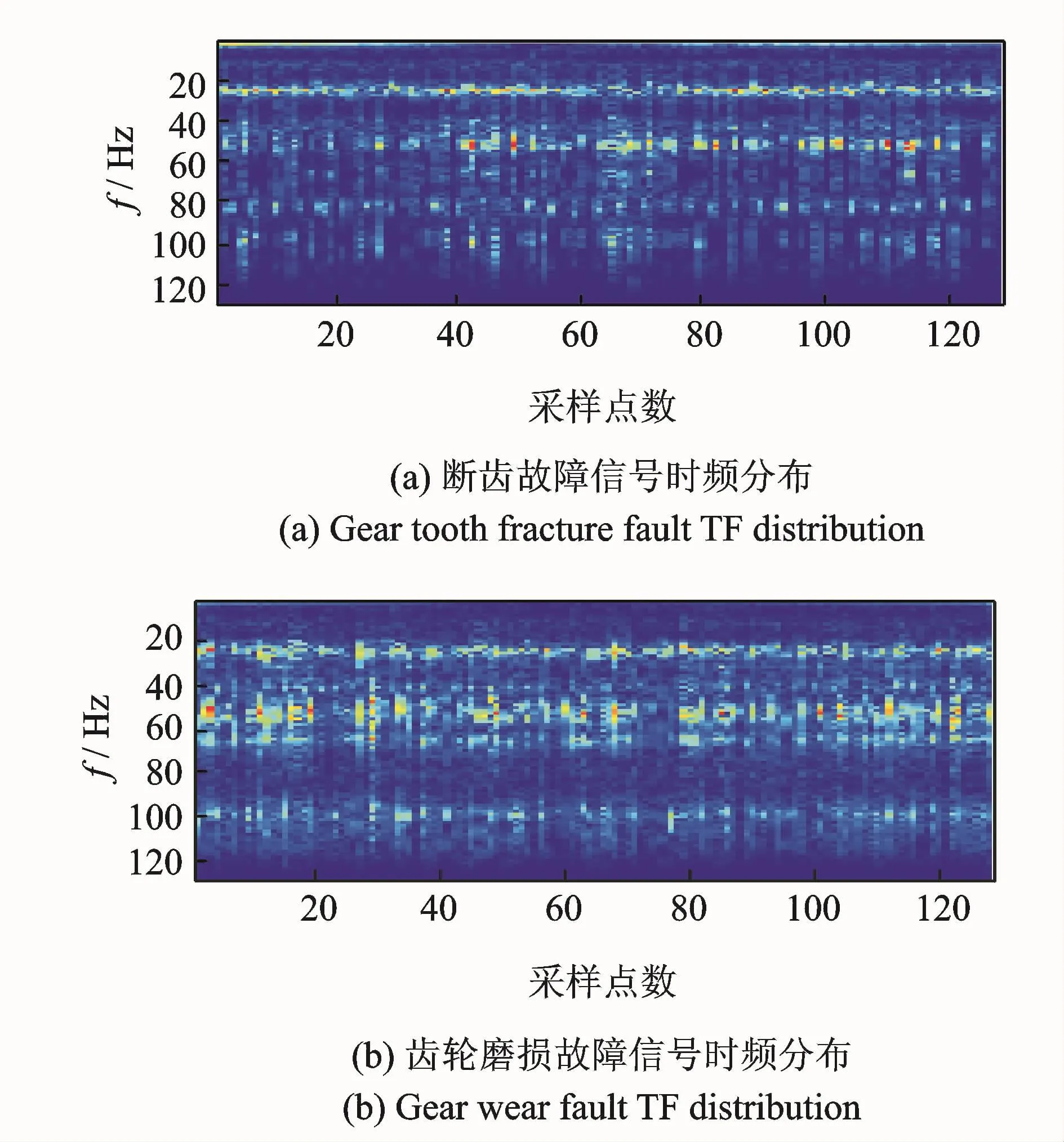
图13 故障源分离信号时频分布Fig.13 Separated fault sources TFdistribution

采用信号干扰比评定分离效果［13］，信号干扰比定义如下

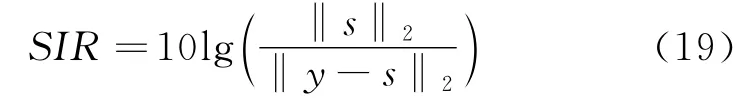
式中 s为源信号的时频分布，y为恢复信号的时频分布。一般在SIR＞10 dB时即可认为源信号得到有效分离。

表1为不同方法的计算结果，通过对比可知，本文方法能够将复合故障源有效分离出来。

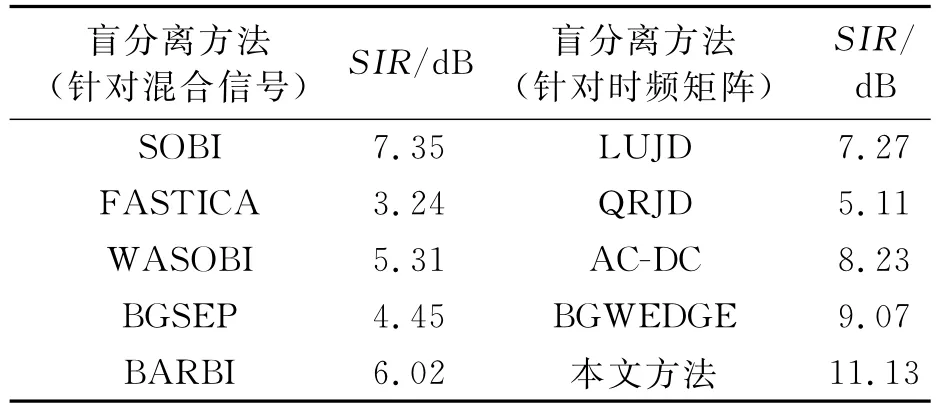
表2 不同盲分离方法SIR值Tab.1 SIR valuae under different BSS methods

6 结 论

(1)多分量调频混合信号二次型时频分布非正交联合对角化盲分离可辨识性可由时延相关矩阵推广得到，对于非平稳相关源信号，通过寻找源自项时频点进行非正交联合对角化，可成功实现盲分离。

(2)利用白化对对分量调频源相交信号去冗余处理，选取自项时频点位置，无需计及源统计特性，准确识别出源信号自项时频点的位置，进而结合均匀加权非正交联合对角化方法进行分解，无需对源信号白化处理，提高了分离效率。

(3)与其他典型方法包括针对信号及针对时频矩阵的算法相比，本文所提方法分离效果具有明显优势，这是得益于将白化预处理应用至相关源中进行去冗余处理，对源概率密度及二阶相关性无特别要求，进行计算自项时频点时减小了误差。由于对角化累积误差，存在最佳自项时频矩阵个数，但总体上，随着对角化个数增大，其分离效果趋于平稳。

(4)非正交联合对角化二次型时频相交信号，利用了时序特性，数学意义明确，仿真及实验表明，所提方法具有明显抗噪能力，能够在含噪情况下分离隐含的分量。通过对转子振动信号降噪处理，能清晰反映转子运行状态；针对断齿与磨损复合齿轮故障源，时频分布呈冲击特性，具有较多分量，所提方法能分离出断齿与磨损复合故障源。

［1］张贤达.现代信号处理［M］.北京：清华大学出版社，2002：486—492 Zhang Xianda.Modern Signal Processing［M］.Beijing：Tsinghua University Publish House，2002.

［2］Tichavsky P，Yeredor A.Fast approximate joint diagonalization incorporating weight matrices［J］.Signal Processing，2009，57(3)：878—891.

［3］Yeredor A.Non-orthogonal joint diagonalization in the least-squares sense with application in blind source separation［J］.Signal Processing，2002，50(7)：1 545—1 553.

［4］Pham D T.Joint approximate diagonalization of positive definite Hermitian matrices［J］.Journal on Matrix Analysis and Applications，2001，22(4)：1 136—1 152.

［5］Afsari B.Simple LU and QR Based Non-orthogonal Matrix Joint Diagonalization［M］.Berlin：Springer，2006：1—7.

［6］Lin F，Meng G.Study on the dynamics of a rotor in a maneuvering aircraft［J］.Journal of Vibration and A-coustics，2003，125(3)：324—327.

［7］Fadaili E M，Moreau N T，Moreau E.Nonorthogonal joint diagonalization/zero diagonalization for source separation based on time-frequency distributions［J］.Signal Processing，2007，55(5)：1 673—1 687.

［8］Aissa-El-Bey A，Linh-Trung N，Abed-Meraim K，et al.Underdetermined blind separation of nondisjoint sources in the time-frequency domain［J］.Signal Processing，2007，55(3)：897—907.

［9］Fevotte C，Doncarli C.Two contributions to blind source separation using time-frequency distributions［J］.Signal Processing Letters，2004，11(3)：386—389.

［10］彭富强，于德介，刘坚.一种基于多尺度线调频基的稀疏信号分解方法［J］.振动工程学报，2010，23(3)：333—338.Peng Fuqiang，Yu Dejie，Liu Jian.Sparse signal decomposition method based on multi-scale chirplet［J］.Journal of Vibration Engineering，2010，23(3)：333—338.

［11］Koldovsky Z，Tichavsky P，Oja E.Efficient variant of algorithm fast ICAfor independent component analysis attaining the cram r-rao lower bound［J］.Neural Networks，2006，17(5)：1 265—1 277.

［12］Tichavsky P，Yeredor A，Koldovsky Z.Afast asymptotically efficient algorithm for blind separation of a linear mixture of block-wise stationary autoregressive processes［A］.Acoustics，Speech and Signal Processing［C］.Florence，Italy，2009：3 133—3 136.

［13］Cichocki A，Zdunek R，Amari S.Nonnegative matrix and tensor factorization［J］.Signal Processing Magazine，IEEE，2008，25(1)：142—145.

NOJD for multi-components FMsource mixed signal separation based on time-frequency distributions

LI Ji-yong1，LI Shun-ming1，TIAN Guo-cheng2，CHEN Xiao-hong3，WANG Yong1
(1.College of Energy and Power Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China；2.Shandong Zhongshi Yitong Group Co.，Ltd.，Jinan 250000，China；3.College of Science，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

Aimed to mixed multi-components FM(Frequency Modulation)sources blind separation problem，a new method named Whitening-Uniformly Weighted Exhaustive Diagonalization using Gauss iteration(W-UWEDGE)is proposed，whitening procedure is used for redundancy compression，there are no constraints on statistical properties，only no overlapping components on whole TFplane condition is required，the nonorthogonal joint diagonalization method is used in complex field.Firstly，identifiability from time-lag plane to quadratic time-frequency plane is extended.Secondly，gradient norm method based on whitening is employed to select autosource(Time-Frequency)TFpoints，then estimated mixed matrix is evaluated by UWEDGE method，meanwhile the Amari error value is calculated with changes of SNR and number of TFmatrixes，numerical performance of several BSS methods aimed to time-history and TFdistribution was compared，the results show that the proposed method W-UWEDGE gains better performance.Lastly，the method is employed in the rotor operating state identification and composite gear fault source separation.Simulation and experiments show that the proposed method can separate multi component FMsources efficiently.

multi-components FMsignal；quadratic time-frequency distribution；whitening；nonorthogonal joint diagonalization；blind source separation

TN911.7

A

1004-4523(2015)04-0633-07

10.16385/j.cnki.issn.1004-4523.2015.04.017

李纪永(1985—)男，博士研究生。电话：18215636567；E-mail：ljynav@163.com

2014-01-06；

2014-11-18

西安交通大学机械结构强度与振动国家重点实验室开放课题(SV2015-KF-01)；中央高校基本科研业务费专项资金资助项目(NZ2015103)；国家自然科学基金青年科学基金资助项目(61403193)