基于移不变稀疏编码的单通道机械信号盲源分离

朱会杰，王新晴，芮 挺，李艳峰，张红涛，赵 洋

(1.解放军理工大学野战工程学院，江苏南京210007；2.防空兵指挥学院，河南郑州450052)

基于移不变稀疏编码的单通道机械信号盲源分离

朱会杰1，王新晴1，芮 挺1，李艳峰1，张红涛2，赵 洋1

(1.解放军理工大学野战工程学院，江苏南京210007；2.防空兵指挥学院，河南郑州450052)

针对特征反复出现的机械信号，提出了一种使用移不变稀疏编码的单通道盲源分离方法。移不变稀疏编码将原始信号看成多个基与系数的卷积，能够根据信号的统计分布，利用信号自身特征自适应地学习到匹配的基和稀疏的系数。在恒定工况下，不同的信号源具有不同的特征，同一信号源的特征结构相似，将学习到的不同特性的基分别重构即可得到相应的源信号。将该方案应用于仿真的齿轮故障和轴承故障振动信号盲源分离问题中，以及用来提取实测的液压泵压力脉动。结果显示，这种方法较其他方法有所改进，所需人工经验少、抗噪能力强、信号恢复精度高、鲁棒性好，适用于单通道机械信号盲源分离，为单通道信号盲源分离提供了一种新思路。

信号处理；移不变稀疏编码；盲源分离；正交匹配追踪；字典学习

引 言

在机械工程领域，很多观测信号都是多种源信号的组合，需要使用盲源分离(blind source separation，BSS)从若干观测信号中恢复出各个源信号。当源信号数量多于观测信号数量是欠定盲源分离，常规盲源分离方法无法奏效。尤其是单通道盲源分离，已被公认为盲信号处理中的挑战性难题［1-2］。

单通道盲源分离已被应用于声 音处理3］、医学［4］、故障诊断［5］、雷达信号分析［6］等多个领域，鸡尾酒会问题本质也属于这一问题。为此，有许多学者尝试解决该问题。针对具有稀疏性的欠定线性瞬时混合盲源分离问题，Roan［7］，Shoko［8］等采用聚类的方法进行了尝试，但对于单通道盲源分离问题，线性稀疏性条件往往不能满足。还有一些学者将源信号分解，增加观测信号的个数，将欠定问题转化为适定或超定问题。成谢锋［2］基于圆周卷积分层将原始信号由一维向量转化成为多维向量，也有一些学者使用经验模态分解(Empirical modes decomposition，EMD)［9-10］、集成经验模态分解［11］、极值域均值模式分解［12］、局域均值分解［13］以及奇异值分解［14］等方法将信号分解成多个分量，增加观测信号的个数，再使用独立分量分析(independent component analysis，ICA)进行盲提取，但这种方式改变了信号的结构特征，受人工经验影响较大，仍不能达到理想的效果。近些年来，稀疏编码被用于解决欠定盲源分离问题，提高了分离的效果，但文献［15］假设源信号的混合矩阵已知，文献［16］使用预先设定的字典对信号的匹配能力仍有待提高。

Smith［17］提出的移不变稀疏编码(Shift invariant sparse coding，SISC)，将信号表示为多个基(特征或原子)与系数的卷积形式，自适应地学习基与系数达到对原信号的稀疏表达。这一理论被发表于《Nature》杂志以来，因其自适应性好、抗噪能力强、所需人工经验少、鲁棒性强等优点，已经引起了广泛关注［3-5，18］。常见的机械信号特征都是重复出现的，比如故障轴承的冲击、往复式活塞的压力变化、液压泵的流量变化等等。在恒定工况下，由于不同的源信号具有不同的特征，同一源信号的特征结构相似，使用SISC学习到这些特征后，分别将各个基进行重构，可得到相应的源信号，实现了单通道机械信号的盲源分离。

1 理论方法

1.1 SISC的原理

稀疏分解理论认为，使用一个包含K个基的过完备字典D=［d1，d2，…，dK］∈Rn×K，单通道信号y∈Rn可以被表示成这些基的线性组合，即y=Dx+ε，其中ε为标准白噪声，向量x∈RK为稀疏的。

SISC将信号看成基与系数的卷积［17］

式中 *表示卷积，dj∈Rm，xj∈Rl是稀疏的，m＜n，l＜n。由稀疏分解理论可知［17］，SISC是依据统计概率对信号进行稀疏表示，只有学习到的基与信号本质特征相匹配时才能足够稀疏地表示原信号。在恒定工况下，不同源信号具有不同的特征，相同的源信号具有类似的特征，可以把不同的基与对应系数的卷积(dj*xj)看作一个源信号或者源信号的一部分。

d和x都是未知的，无法同时对它们进行求解，但可以利用最大后验概率将该问题转化为系数求解和字典学习两个过程，反复迭代，直到收敛或达到停止条件［17］，下面依次介绍这两个过程［18］。

1.1.1 系数求解

本文选用正交匹配追踪(Orthogonal matching pursuit，OMP)求解稀疏表示的系数，这一过程相当于固定所有的基，求解对应的系数

其中·表示非零系数的个数，T0为稀疏度。

OMP是匹配追踪(Matching pursuit，MP)的改进，也是一种迭代的贪婪算法［19］。OMP每次选取与信号最匹配的原子之后，都要将全部所选原子正交化处理，并将它们重新在原始信号上进行投影。这种方式保证了残余与所有已选原子正交，并且选取的原子都互不相关，因此残差信号的分解过程也非常迅速。OMP加快了收敛速度又保证了最优迭代性，因此本文选用OMP。

令D={gj｝1K为用于信号稀疏分解的过完备原子库，其中gj为dj补零后的原子，其长度与原信号相同，且‖gj‖=1。OMP过程如下：

(1)设y为待处理的信号序列，信号残余r0=y，已选原子的集合ψ-1为空集，迭代次数n=0。

(3)更新已选原子的集合ψn=ψn-1∪ {｝。

(4)根据最小二乘法计算投影系数an=(ψnTψn)-1·ψnTy，因此重构信号y~n=ψnan，残余rn=y-n。

(5)更新迭代次数n=n+1，判断残余信号与原始信号的能量比‖rn‖2/‖y‖2是否小于设定值，或者是否达到稀疏度T0，若不满足则返回步骤(2)，若满足则输出重构信号~yn，残余为rn。

在选择最匹配的原子时，需要大量的内积运算，使用快速卷积算法可以加快运算。

1.1.2 字典学习

字典学习相当于固定所有的系数，求解与信号最匹配的基：

直接求解该问题的计算量很大，已经有学者提出多种快速优化算法。Olshausen［20］和Blumensath［3-4］利用差分求导来求取基的数值解，Szlam［21］使用主成分法进行基的更新。Grosse［18］使用了一种巧妙的优化方式，将这一问题转化到频域求解，本文也借鉴了这种思想［18］。由帕斯瓦尔定理可知，式(4)可以转化为下面的优化问题

式中 f对应于频率，系数λ∈RK，单位向量l∈RK，并且

使用牛顿法对参数λ进行优化，代入式(7)即可完成对基的更新［18］。

1.2 基于SISC的单通道信号盲源分离流程

采用本文方法对恒定工况下的单通道信号进行盲源分离的流程如图1所示，步骤如下：

(1)首先对算法进行初始化，设定最大迭代次数、稀疏度等。

(2)对观测信号进行移不变稀疏分解，求得对应于不同源信号的基，并根据基与对应的重构信号的特性确定其来源。

(3)将不同的基和对应的系数进行重构，得到不同的源信号。

图1 本文方案的流程图Fig.1 The flow chart of proposed scheme

2 实验验证

2.1 仿真实验验证

齿轮和轴承是常用的机械部件，经常将它们组合使用，因此对它们的信号进行盲分离具有实际意义。根据齿轮和轴承的故障模型［22］，仿真了一个源信号为齿轮故障信号和轴承故障信号线性叠加的单通道含噪信号。齿轮故障时会出现幅值调制和相位调制现象，它的振动信号的模型为

式中 k为谐波成分的阶次；Ak(t)，φk分别为第k次谐波成分的幅值和相位；fm为啮合频率。

故障轴承的冲击响应可以简化为

式中 a( t)为调幅幅值；p为衰减系数，代表了冲击衰减的快慢；fb为共振的固有频率；φ为相位。

因此故障轴承的振动信号为

这里 m为冲击的次数，T为冲击的周期，τm≈0.01～0.02 T，为随机滑动。

仿真信号y=ym+yb+yn，yn为高斯白噪声，信噪比为6 dB。各参数取值为：采样频率fs=12 000 Hz，信号长度为4 096点，K=5，Ak(t)=2.5·［sin( 60 π t)+2］/k，fm=340 Hz，φk=kπ/4；p=1 200，φ=0，fb=3 400 Hz，a( t)=20·［sin( 60 π t)+2］，T=0.01 s。观测信号y的波形如图2所示(由于篇幅有限，仅取其中1 000个点，下同)，源信号yb，ym和yn的波形如图3所示。

图2 观测信号Fig.2 Measured signal

图3 源信号Fig.3 Original signals

由图2可知，轴承和齿轮故障信号混合在一起，已经无法看出它们的原始波形。从图3可以看出噪声的幅值已经与部分轴承和齿轮故障的冲击接近，噪声污染比较严重。

使用SISC对观测信号进行分解，首先要确定源信号的个数。盲源分离包括盲源个数的估计和盲源的分离两个部分，本文重点研究盲源的分离，盲源个数的估计可以参考其他学者提出的方法，比如文献［2，14，16］的方法。本文提出了一种使用基的频域相关度进行源数估计的方法。对于未知类别的源信号，首先假定一个比预估源数大一些的数作为基的个数进行分解，然后计算各基之间的相关度，如果有明显相关的情况，则减少基的个数再次对信号分解，以此类推，直到没有任何两个基有明显相关。定义相关度pi，j=ρ［FFT( di)，FFT( dj ) ］，其中FFT表示傅里叶变换，ρ(x，y)表示相关系数。这里使用基的傅里叶变换而非基本身求取相关系数是为了消除基的平移所引起相关系数的变化。

图4 学习到的4个基Fig.4 Learned four bases

大量实验表明，当Pij＞0.7时，可以认为基di与dj相关，应减少源数的个数；当Pij＜0.5时，可以认为基di与dj相关性不强，应属于不同的源信号。而0.5＜Pij＜0.7时则要根据实际情况进一步讨论或者参考其他方法。

对于上述仿真信号y，首先根据经验预估一个比真实源数大的值作为基的个数，进行试探性分解，这里首先选用4个基，基的长度都选为35个点，稀疏度T0=180，最大迭代次数设为30次。基的波形如图4所示，各个基之间的相关系数如表1所示。

表1 基的相关度Tab.1 The correlations between bases

由表1和图4可知，基1与基2，基1与基4，基2与基4相互之间都存在着高度相关，并且它们的波形也比较相似，它们应该属于同一个信号源。为了谨慎起见，将源信号个数也即基的个数减小为3，波形如图5所示，基之间的相关度如表2所示。

由图5、表2可知，基1与基3相关度较高，波形相似，基2与基1或基3的相关度低，波形结构差异大，因此源数应该为2。选择源数(基的个数)为2进行分解的波形如图6所示，它们的相关度为0.27，相关度较低，波形结构差异大，可以推断该源信号包含两个源信号。

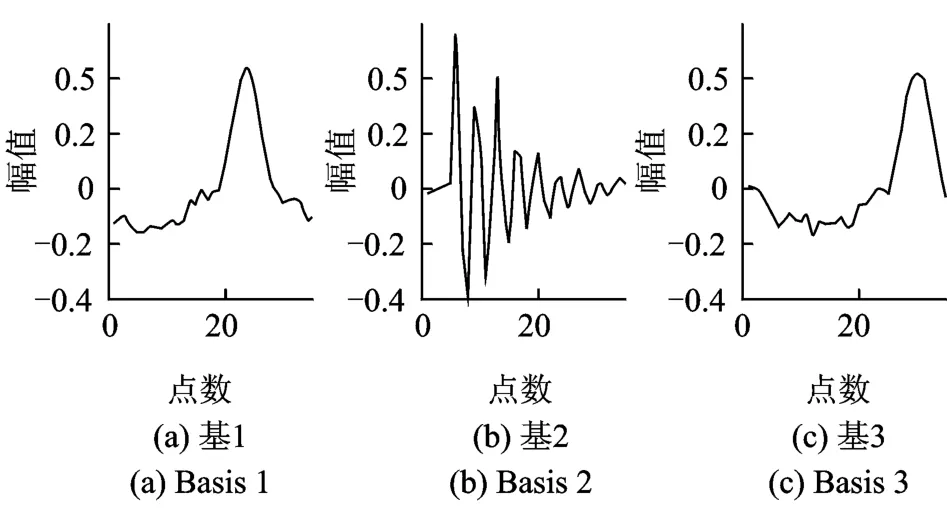
图5 学习到的3个基Fig.5 Learned three bases

表2 基的相关度Tab.2 The correlations between bases

由图6可知，基1是一个衰减震荡，属于典型的轴承故障信号，基2是一个单峰冲击，符合齿轮故障信号的特征。分别将它们与对应的系数进行重构，得到两个估计的源信号，如图7(a)，(b)所示。由图7(a)可以看出这是一个调幅的周期性冲击振荡，再次验证了该信号为轴承故障信号。而图7(b)为调幅的周期性冲击，为典型的齿轮故障信号。信号残余为白噪声，如图7(c)所示。本文方案准确地将轴承故障信号和齿轮故障信号分离和恢复出来，仅在标注处与原信号有微小误差，保留了源信号的细节。此外由于在SISC的模型中已经将高斯白噪声考虑在内，其分解效果受噪声干扰很小，抗噪能力强。

为进一步验证该方法的有效性，还与其他学者的方法进行了对比。李志农［9］用EMD将源信号分解为多个分量，之后使用ICA进行盲分离，使用他的方法所得结果如图8所示。董绍江［16］使用数学形态法(Mathematical morphology，MM)进行滤波，之后使用基于Gabor原子的匹配追踪将源信号进行分解，把分解信号与源信号组合成新的观测信号，再使用快速核独立分量分析(Fast KICA)进行盲源分离。参考文献［16］，并经实验对比发现，形态结构元素为扁平型、长度为3、幅值为0时效果较好，故选用该形态结构元素，盲分离的结果如图9所示。

图6 学习到的2个基Fig.6 Learned two bases

图7 本文方法估计的源信号Fig.7 Estimated signals by proposed method

为了进一步验证这几种方法的效果，分别使用信噪比(Signal to noise ratio，SNR)和均方误差(Mean square error，MSE)对估计的源信号进行评价，5次实验平均的结果如表3所示。

表3 不同方法效果对比Tab.3 The comparison of different algorithms

图8 估计的源信号(EMD+ICA)Fig.8 Estimated signals by EMD+ICA

图9 估计的源信号(MM+MP+Fast KICA)Fig.9 Estimated signals by MM+MP+Fast KICA

由图8，9和表3可知，EMD+ICA和MM+MP+Fast KICA估计的轴承故障信号yb和齿轮故障信号ym都发生了明显的失真，尤其是估计的轴次试验的平均结果如图10所示。随着噪声的增加，本文方法分解的性能有所下降，但无论在SNR还是MSE的表现上，都明显优于EMD+ICA和MM+MP+Fast KICA。实验结果表明本文方法具有良好的鲁棒性，在不同信噪比下均具有一定优势。承故障信号yb都混入了大量的噪声，而且在SNR和MSE的对比中也都不如本文方案优异。

为了验证本文方法在不同信噪比下的性能，对仿真信号依次添加1～8 dB的白噪声，然后计算信号yb与ym的信噪比与均方误差，并与EMD+ICA方法以及MM+MP+Fast KICA方法进行对比，5

图10 不同信噪比下各种方法效果对比Fig.10 The comparison of different algorithms for different SNR

2.2 在液压压力信号中的应用

图11为液压泵压力信号采集平台，液压泵转速为900 r/min，液压泵有7个柱塞，采样频率为5 000 Hz。在测试过程中，压力信号受到了电机、变频器的电磁脉冲干扰，信号被严重污染。实测压力信号如图11(a)所示，可见油压脉动已经被电磁干扰和白噪声所淹没，为此使用SISC对其进行盲源分离，提取油压脉动成分。首先按照2.1节所述方法确定源数为2，因此选用2个基，一个用来匹配压力脉动，一个来匹配电磁脉冲，分解的信号残余则为白噪声。设定基的长度为48个点，稀疏度为T0=150，最大迭代次数为20次。

两个基的波形如图12所示，盲源分离结果如图13(b)，(c)，(d)所示。由图12中可以看出，基1具有短时脉冲特性，基2形状是先降后升，类似于压力脉冲中压力的变化波形，图13(b)和(c)分别是由基1和基2的重构图形，由重构波形可以进一步看出基1和基2分别匹配电磁干扰和压力脉动。结果显示，使用本文方法能将压力脉动成分准确地从原信号中提取出来，消除了电磁干扰和白噪声的影响，为下一步的分析奠定了基础。

图11 液压泵压力信号采集平台Fig.11 The test rig of pressure signal acquisition for hydraulic pump

图12 学习到的基Fig.12 Learned bases

图13 原始压力信号与分解结果Fig.13 Original pressure signal and its decompositions

3 结 论

本文基于SISC提出了一种对恒定工况下单通道信号进行盲源分离的新方法，并将其用于源信号为仿真的轴承故障信号和齿轮故障信号的盲分离问题，以及提取实测压力信号的脉动成分，并与其他学者的方法进行了对比。经实验验证，这种方法不仅能够实现单通机械信号的盲源分离，为单通道盲源分离以及盲源分离提供了一种新的思路，而且信号恢复精度高，具有较强的抗噪能力和鲁棒性，是一种优异的盲分离方法。

［1］张赟，李本威，贾舒宜，等.航空发动机混叠振动信号的欠定盲源分离方法［J］.推进技术，2014，35(04)：552—558.Zhang Yun，Li Ben-wei，Jia Shu-yi，et al.Underdetermined blind source sparation of aeroengine vibration signal mixtures［J］.Journal of Propulsion Tchnology，2014，35(04)：552—558.

［2］成谢锋，马勇，张学军，等.一种不用先验知识的单路混合信号的盲源分离新方法［J］.电子学报，2011，39(10)：2 317—2 321.Cheng Xie-feng，Ma Yong，Zhang Xue-jun，et al.Asingle-channel mixed signal BSS new method without using the prior knowledge［J］.Acta Electronica Sinica，2011，39(10)：2 317—2 321.

［3］Blumensath T，Davies M.Sparse and shift-invariant representations of music［J］.Audio，Speech，and Language Processing，IEEE Transactions on，2006，14(1)：50—57.

［4］Blumensath T，Davies M.Shift-invariant sparse coding for single channel blind source separation［J］.SPARS，2005，5：75—78.

［5］Tang H，Chen J，Dong G.Sparse representation based latent components analysis for machinery weak fault detection［J］.Mechanical Systems and Signal Processing，2014，http：//dx.doi.org/10.1016/j.ymssp.2014.01.011.

［6］陈晓军，成昊，唐斌.基于ICA的雷达信号欠定盲分离算法［J］.电子与信息学报，2010，32(4)：919—924.Chen Xiao-jun，Cheng Hao，Tang Bin.Underdetermined blind radar signal separation based on ICA［J］.Journal of Electronics&Information Technology，2010，32(4)：919—924.

［7］Roan M，Erling J，Sibul L.Anew，non-linear，adaptive，blind source separation approach to gear tooth failure detection and analysis［J］.Mechanical Systems and Signal Processing，2002，16(5)：719—740.

［8］Araki S，Sawada H，Mukai R，et al.Underdetermined blind sparse source separation for arbitrarily arranged multiple sensors［J］.Signal Processing，2007，87(8)：1 833—1 847.

［9］李志农，吕亚平，范涛，等.基于经验模态分解的机械故障欠定盲源分离方法［J］.航空动力学报，2009，24(8)：1 886—1 892.Li Zhi-nong，Lv Ya-ping，Fan Tao，et al.Underdetermined blind source separation method of machine faults based on empirical mode decomposition［J］.Journal of Aerospace Power，2009，24(8)：1 886—1 892.

［10］孙洁娣，郝雅立，温江涛，等.基于EMD的高压燃气管道泄漏信号欠定盲分离方法［J］.振动与冲击，2013，32(18)：81—86.Sun Jie-di，Hao Ya-li，Wen Jiang-tao，et al.Underdetermined blind source separation method of pipeline leakage signals based on empirical mode decomposition［J］.Journal of Vibration and Shock，2013，32(18)：81—86.

［11］刘佳，杨士莪，朴胜春.基于EEMD的地声信号单通道盲源分离算法［J］.哈尔滨工程大学学报，2011，32(2)：194—199.Liu Jia，Yang Shi-e，Piao Sheng-chun.The single channels eismic-acoustic signal blind-source separation method based on EEMD［J］.Journal of Harbin Engineering University，2011，32(2)：194—199.

［12］孟宗，梁智.基于EMMD和BSS的单通道旋转机械故障诊断方法［J］.仪器仪表学报，2013，34(3)：635—642.Meng Zong，Liang Zhi.Fault diagnosis method for single channel rotating machinery based on EMMD and BSS［J］.Chinese Journal of Scientific Instrument，2013，34(3)：635—642.

［13］李志农，刘卫兵，易小兵.基于局域均值分解的机械故障欠定盲源分离方法研究［J］.机械工程学报，2011，47(7)：97—102.Li Zhi-nong，Liu Wei-bing，Yi Xiao-bing.Underdetermined blind source separation method of machine faults based on local mean decomposition［J］.Journal of Mechanical Engineering，2011，47(7)：97—102.

［14］申永军，杨绍普，孔德顺.基于奇异值分解的欠定盲信号分离新方法及应用［J］.机械工程学报，2009，45(8)：64—70.Shen Yong-jun，Yang Shao-pu，Kong De-shun.Newmethod of blind source separation in under-determined mixtures based on singular value Decomposition and application［J］.Journal of Mechanical Engineering，2009，45(8)：64—70.

［15］余丰，奚吉，赵力，等.基于CS与K-SVD的欠定盲源分离稀疏分量分析［J］.东南大学学报：自然科学版，2012，41(6)：1 127—1 131.Yu Feng，Xi Ji，Zhao Li，et al.Sparse presentation of underdetermined blind source separation based on compressed sensing and K-SVD［J］.Journal of Southeast University(Natural Science Edition)，2012，41(6)：1 127—1 131.

［16］董绍江，汤宝平，张焱.基于最优匹配跟踪算法的单通道机械信号盲源分离［J］.振动工程学报，2013，25(6)：724—731.Dong Shao-jiang，Tang Bao-ping，Zhang Yan.Blind source separation of single-channel mechanical signal based on optimal matching pursuit algorithm［J］.Journalof Vibration Engineering，2013，25(6)：724—731.

［17］Smith E C，Lewicki MS.Efficient auditory coding［J］.Nature，2006，439(7079)：978—982.

［18］Grosse R，Raina R，Kwong H，et al.Shift-invariance sparse coding for audio classification［A］.Conference on Uncertainty in AI［C］.2007：149—158.

［19］Needell D，Vershynin R.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit［J］.Foundations of Computational Mathematics，2007，9(3)：317—334

［20］Olshausen B A.Sparse coding of time-varying natural images［A］.Proceeding of Internatinal Conference of Independent Component Analysis and Blind Source Separation(ICA)［C］.2000：603—608

［21］Szlam A，Kavukcuoglu K，LeCun Y.Convolutional matching pursuit and dictionary training［OL］.http：//ar Xiv preprint ar Xiv：1010.0422，2010.

［22］Sawalhi N，Randall R.Simulating gear and bearing interactions in the presence of faults：Part I.The combined gear bearing dynamic model and the simulation of localised bearing faults［J］.Mechanical Systems and Signal Processing，2008，22(8)：1 924—1 951.

Shift invariant sparse coding for blind source separation of single channel mechanical signal

ZHU Hui-jie1，WANG Xin-qing1，RUI Ting1，LI Yan-feng1，ZHANG Hong-tao2，ZHAO Yang1

(1.College of Field Engineering，PLAUniversity of Science and Technology，Nanjing 210007，China；2.PLAAir Defense Forces Command College，Zhengzhou 450052，China)

For the single channel mechanical signal with repeated features，the method for blind source separation based on shift invariant sparse coding was proposed in this paper.In the literatures of shift invariant sparse coding，a signal is described as the convolutions of multi bases and their coefficients.According to statistical distribution of a signal，shift invariant sparse coding could adaptively learn its bases and the sparse coefficients from the structures of the signal itself.Under stable condition，different signal sources have different features，and the features from the same source are similar，thus the learned bases with different features could be used to reconstruct corresponding signal sources.This scheme was applied in the blind source separation of simulated vibration signals of faulty gear and bearing，as well as the extraction of pressure pulsation of hydraulic pump.The result showed that this algorithm has improved a lot compared to other algorithms，and this algorithm needs less expertise，has strong anti-interference ability，in addition，it is robust and could recover original signals more accurately.Therefore，

this technique is appropriate to blind source separation for single channel mechanical signal，and provides a new way for single channel blind source separation.

signal processing；shift invariant sparse coding；blind source separation；orthogonal matching pursuit；dictionary learning

TN911.7；TH165+.3

A

1004-4523(2015)04-0625-08

10.16385/j.cnki.issn.1004-4523.2015.04.016

朱会杰(1987—)，男，博士研究生。电话：(025)80821440；E-mail：zhuhuijiehao@163.com

2014-05-03；

2014-07-18

国家自然科学基金资助项目(61472444)