双树复小波和局部投影算法在齿轮故障诊断中的应用
2015-08-07胥永刚赵国亮马朝永杨红玉
胥永刚,赵国亮,马朝永,杨红玉
(北京工业大学机电学院先进制造技术北京市重点实验室,北京100124)
双树复小波和局部投影算法在齿轮故障诊断中的应用
胥永刚,赵国亮,马朝永,杨红玉
(北京工业大学机电学院先进制造技术北京市重点实验室,北京100124)
齿轮故障振动信号往往表现为非线性非平稳特性,并且早期故障振动信号往往包含较强的背景噪声,不利于故障特征的提取。针对该问题,提出了基于双树复小波变换和局部投影算法的齿轮故障诊断方法。首先,对故障信号进行双树复小波变换,得到不同尺度下的小波系数和最后一层的尺度系数,并计算各层小波系数的模与相角。然后,选择模周期性较强的小波系数或尺度系数进行局部投影算法处理,得到周期性增强的系数的模,并选择合适的阈值进行软阈值处理。最后,利用处理后的系数进行双树复小波重构,从而提取出齿轮故障特征信号,进行希尔伯特包络解调分析便能准确地得到故障特征频率。仿真信号和工程应用表明,该方法能够有效地提取齿轮故障特征信息,提供了一种齿轮故障特征提取的新方法。
故障诊断;双树复小波变换;局部投影算法;软阈值;齿轮
引 言
由于故障产生机理复杂,齿轮故障振动信号往往表现为非线性非平稳特性,并且包含强烈的背景噪声,对齿轮早期故障的诊断造成了很大困难[1]。因此,对齿轮早期故障诊断方法的研究具有重要的理论价值和实际意义。
双树复小波变换作为传统离散小波变换的改进方法,在克服了平移不变性及频率混叠等缺陷的同时,还具有完全重构性、较小的数据冗余以及良好的方向选择性[2]。目前,该方法已经成功应用于图像处 理[3-4]、语 音识 别[5]、地 震 监测[6]及 故障 诊断[7-9]等领域。
局部投影算法将时间序列扩展到高维相空间,利用相空间投影法,能够将信号的背景信号、特征信号及噪声分解到不同子的空间,从而达到将其分离的目的[10],能够在分离特征信号的同时有效地抑制噪声成分,并增强周期性成分。自提出以来,该方法已经在生物医学电信号[11-12]及故障诊断[13-14]等领域有了成功的应用。
本文提出了双树复小波变换与非线性时间序列局部投影算法相结合的齿轮故障诊断方法,并将其成功应用于钢铁厂高线轧机齿轮箱的故障诊断。仿真信号和工程实例证明:该方法能够成功、有效地提取齿轮的早期故障特征信息。
1 双树复小波变换
Kingsburg提出的双树复小波变换利用互为近似希尔伯特变换对的两树实小波滤波器组来进行小波分解与重构,分别称为实部树与虚部树。其小波函数可以表示为如下复数形式
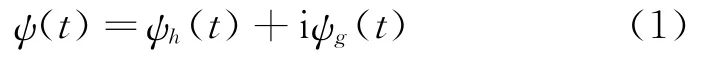
式中 ψh(t),ψg(t)表示两个近似互为希尔伯特变换对的实小波。
双树复小波变换的两树滤波器组在分解和重构过程中并无数据交换,因此,实部树的小波系数和尺度系数可以通过下式获得。
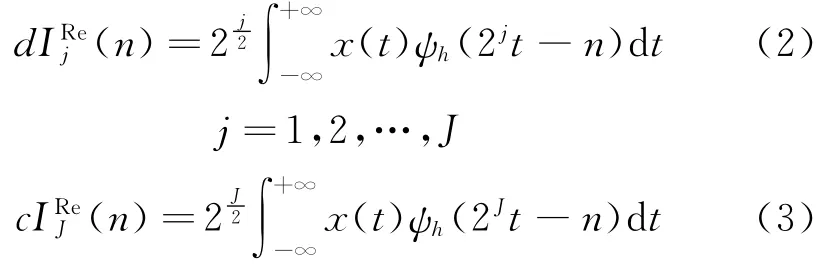
同理,虚部树小波变换的小波系数和尺度系数具有相同的表示形式。

综合两树实小波变换的结果,可以得到双树复小波变换的小波系数和尺度系数如下:
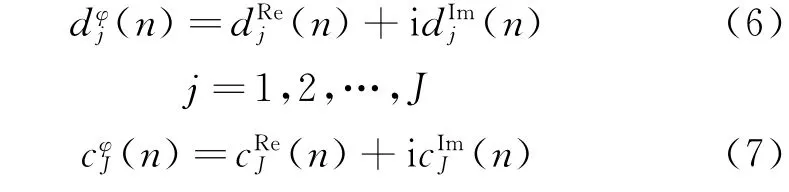
重构为分解的逆过程,重构信号可以表示为:
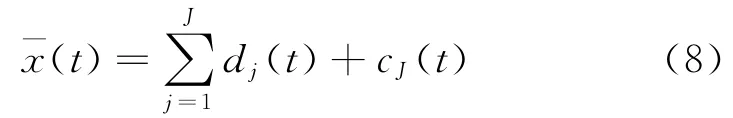
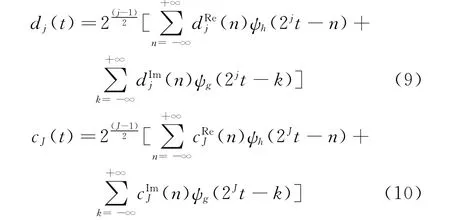
双树复小波变换分解和重构的过程如图1所示。两树滤波器组分别完成实虚部树的实小波变换与重构。实部树滤波器组中,h0代表低通滤波器,h1代表高通滤波器;同理,g0与g1分别代表虚部树的低、高通滤波器,重构过程由相应的重构滤波器完成。
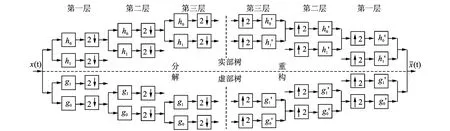
图1 双树复小波变换的分解和重构过程Fig.1 Decomposition and reconstruction process of dual-tree complex wavelet transform
2 非线性时间序列局部投影算法原理
非线性时间序列分析方法的基本思想是:将非线性时间序列进行相空间重构,通过局部投影方法将背景信号,特征信号以及噪声投影到不同的子空间,同时抑制时间序列中的随机噪声成分,从而达到将其分离的效果[10]。
假设动力系统的非线性状态方程如下

当F未知时,xk+1可以近似为状态xk在状态{xk},k=1…N中u(n)邻域内的线性化估计,可以表示为下式的形式
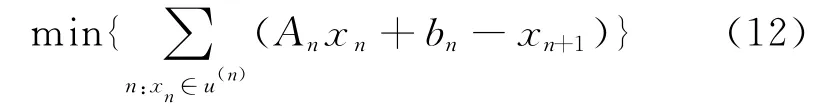
参数An,bn可以通过式(12)解得。不存在噪声时,Anxn+bn-xn+1=0,系统处于超平面内。当受到噪声干扰时,即yn=xn+ηn时,对信号进行相空间重构,则噪声处于超平面外的相空间中。可以通过将yn投影到该超平面来进行信号的消噪。
对于任意时间序列sn,可以重构m维相空间

式中 τ为延时时间,m为嵌入维数。该相空间与原系统具有相同的动力学特性,与原系统的动力学行为是微分同胚的。通过sn的式(12)的最小化解来对sn进行修正。上述投影降噪方法称为非线性空间局部投影算法。其具体步骤如下:
(1)对于时间序列S=s1,s2,…,sn,确定延时时间τ及嵌入维数m,进行m维相空间重构。
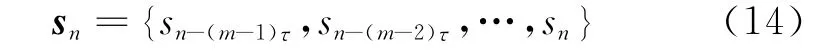
(2)确定邻域半径ε,寻找满足‖sk-sn‖<ε的向量及其个数N。
(3)计算满足条件的N个向量的质心
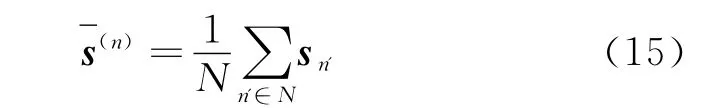
(4)计算协方差矩阵
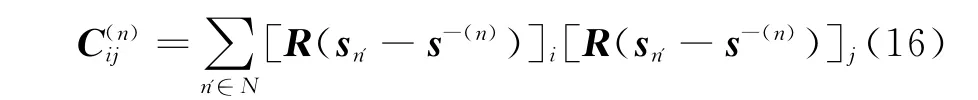
式中 R为对角权重矩阵,其作用为抑制相点的首尾元素所产生的畸变,故R11和Rmm选取较大值,其他Rii取值为1。
(5)消除噪声。计算协方差矩阵C(n)ij的特征值与特征向量,选取特征值最小的Q个特征向量aq,q=1,…,Q,按照下式对相空间sn进行修正。

(6)返回步骤(2),直到所有的相点处理完。
修正完毕后,将sn中的标量信号取平均值即可重构得到降噪后的信号。
参数选择对算法的降噪效果有直接影响,目前参数的确定方法已经较为成熟。目前确定延迟时间的方法有:自相关函数法、平均位移法、复自相关法及平均互信息法等;嵌入维数可以通过几何不变量法、虚假临近点法及改进虚假邻点法等方法确定,文献[11]对上述几种方法进行了比较与总结。
本文中滤波参数的确定选用较为常用的自相关函数法与效果较好的改进虚假邻点法。邻域半径的选择较为简单,只需略大于噪声的平均幅值即可。Q一般为3~5。
3 DT-CWT与局部投影算法相结合的齿轮故障诊断方法
双树复小波变换得到的小波系数为复数形式,其模在信号冲击特征明显处幅值较大而且变化较为平稳,周期性更为明显,更加适合非线性时间序列局部投影算法的处理要求,因此选择对小波系数的模进行局部投影算法处理。具体实施步骤如下:
(1)对齿轮故障信号进行双树复小波变换,得到不同层的系数矩阵,计算各层系数模并保留相位信息。
(2)选择系数模周期性较为明显的层的系数,选用合适的τ,m及Q值对其模进行单次或多次非线性局部投影算法处理;当系数模的周期性不明显时可以利用系数谱(即系数模去恒流量后的傅里叶谱)进行周期分析,当系数模存在周期性时其系数谱必定会出现倍频现象。
(3)选取合适的阈值对周期增强之后的小波系数模进行软阈值处理,以消除恒流成分对重构结果的影响,然后利用保留的相位信息将处理后的模还原为小波系数,以便重构。
(4)将处理后的小波系数进行单支重构,即可提取出齿轮故障特征信号,再进行希尔伯特包络解调分析便可准确地得到故障特征频率。
4 仿真分析
构造齿轮故障仿真信号,序列x(t)由10段衰减正弦信号x1(t)组成,x1(t)定义如下
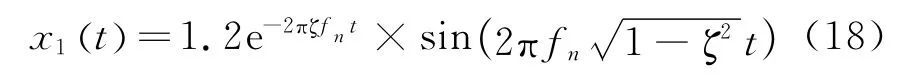
式中 fn=2 000,ζ=0.1。采样频率为10 k,每段100个点,总点数N=1 000。通过向x(t)添加信噪比为-5 dB的高斯白噪声得到噪声污染信号y(t)。x(t)与y(t)的时域波形如图2所示。

图2 x(t)与y(t)的时域波形Fig.2 Waveform of x(t)and y(t)
图2可见,与x(t)相比,y(t)中已经不能发现明显的周期性冲击成分。将y(t)进行5层双树复小波分解,并绘制小波系数的模,如图3所示。

图3 双树复小波分解各层系数幅值Fig.3 The magnitude of the DT-CWT coefficients
图3中,d1~d5表示1~5层小波系数幅值,c5为第5层尺度系数幅值,可以看出d2的周期性较为明显,故选择对d2进行局部投影算法处理,以增强序列中的周期性成分并抑制随机噪声。
利用自相关函数法求取延迟时间,如图4所示。
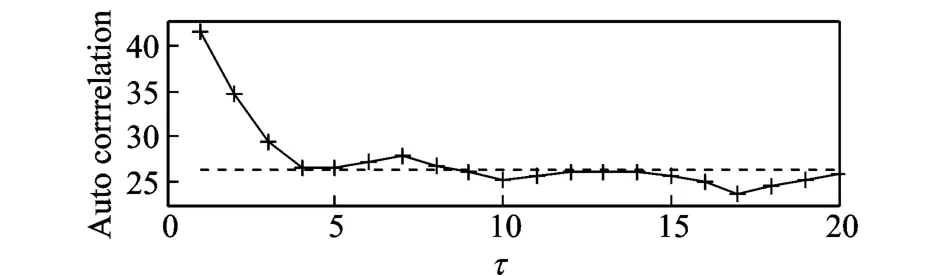
图4 自相关函数法确定延迟时间Fig.4 Choose the time delay using autocorrelation function
根据改进虚假邻点法确定嵌入维数,如图5所示。

图5 改进虚假邻点法选取嵌入维数Fig.5 Choose the embedding dimension using Cao method
E1,E2为两个计算指标,其随嵌入维数的变化曲线如图5。嵌入维数的选取原则:选取使E1与E2变化平稳且接近的m值即可,本文选择m=13。
邻域半径ε=0.5,R11和Rmm为103,Q=3。采用同样的参数进行两次非线性时间序列局部投影算法处理,结果如图6所示。
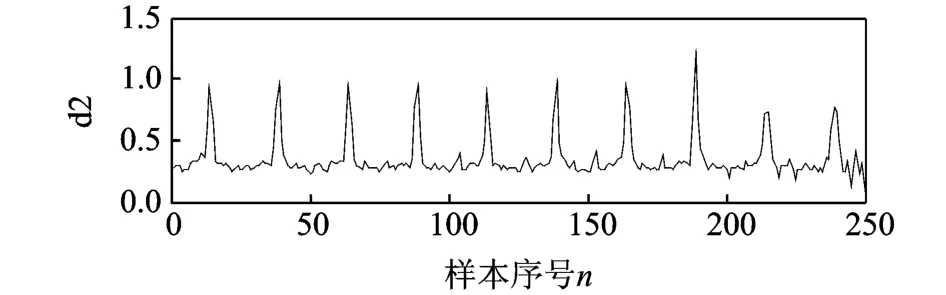
图6 d2局部投影算法降噪结果Fig.6 Denoising result by local projective method
图6可见,与图3中d2相比,序列中的噪声被显著地降低,周期性成分被成功地提取出来。为了进一步在时域凸显信号的周期性,进一步对其进行阈值为0.3的软阈值处理,以消除直流量的影响(约为0.3)。还原为小波系数后,对其进行单支重构,便可得到故障特征信号,如图7所示,其幅值谱如图8所示。双树复小波变换能够将信号中的周期性成分提取出来,如图7(a)所示,但是依然存在较强的噪声。对双树复小波变换小波系数进行局部投影算法降噪后,能够显著降低信号中的随机噪声,提取出信号中的周期性成分。
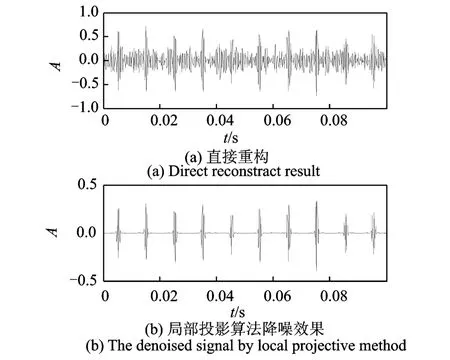
图7 重构信号对比Fig.7 Comparison of direct reconstruction signal and the denoised one by local projective method
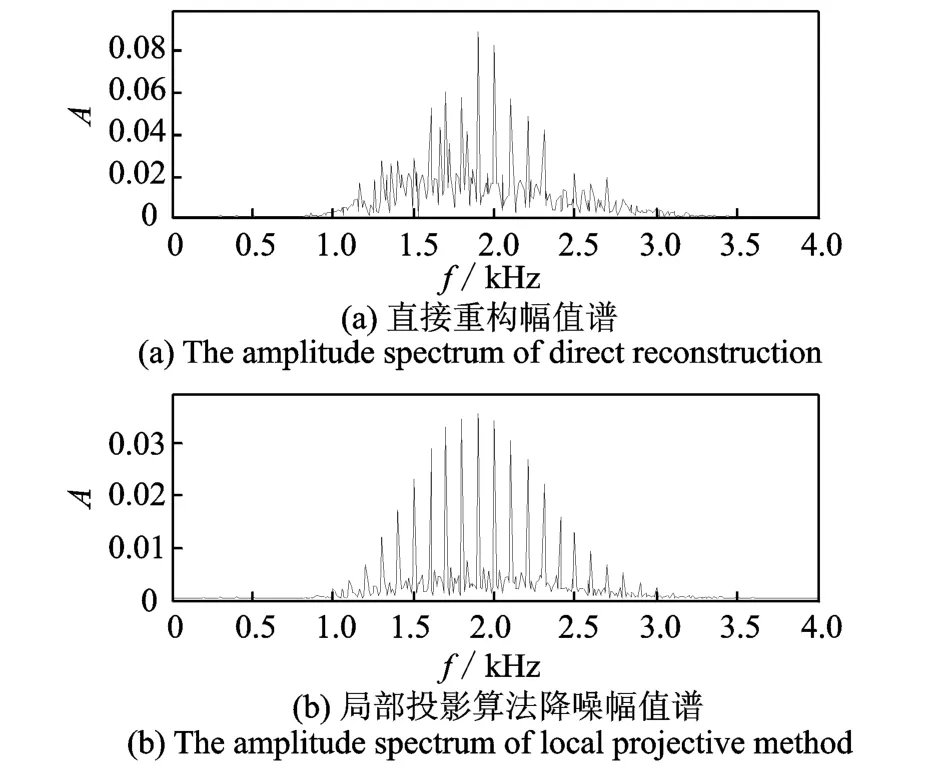
图8 重构信号幅值谱对比Fig.8 The Fourier amplitude spectrum of direct reconstruction signal and the denoised one
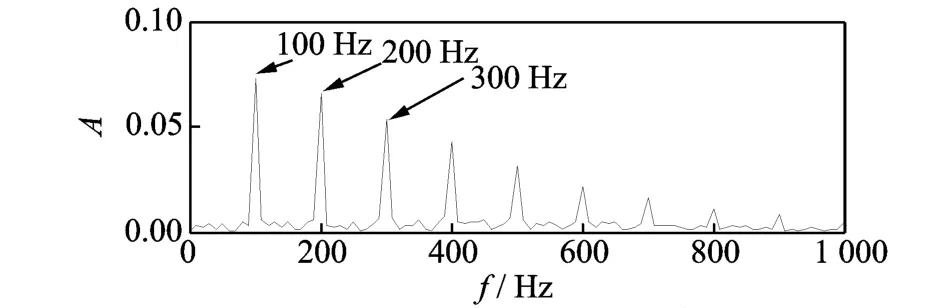
图9 希尔伯特包络解调谱Fig.9 Hilbert envelope spectrum of the denoised signal
对降噪后的信号进行希尔伯特包络解调分析,便可以准确得到信号的故障特征频率,如图9所示。上述结果表明,双树复小波与局部投影算法相结合能够有效地提取信号中的故障特征频率。
5 工程应用
某钢铁公司高线厂第25架轧机于2007年8月1日发现齿轮箱振动异常,开箱检查发现Z5/Z6齿轮出现打齿故障,如图10所示。

图10 故障齿轮照片Fig.10 Photo of the damaged gear
为了能够在故障早期发现故障,现对6月30日的齿轮箱振动数据进行分析,采样点数为2 048,采样频率为12 000 Hz。经计算,故障特征频率为76.172 Hz。该数据的波形及频谱如图11所示。时域波形中没有发现明显故障特征信息,频谱中虽出现少数边频成分但不明显,频率成分较为复杂不能准确识别出故障齿轮的特征频率。
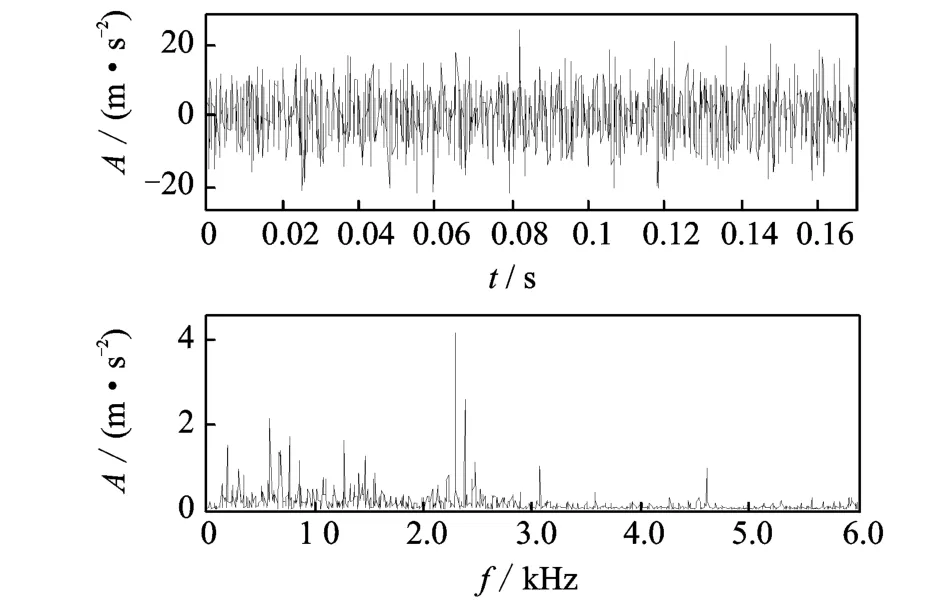
图11 6月30日故障齿轮波形及频谱Fig.11 Waveform and spectrum of data on June 30
对该信号进行5层双树复小波变换,得到前5层的小波系数与第5层的尺度系数,并计算其模(如图12所示)选择周期性较为明显的d2应用局部投影算法进行降噪与周期性增强。利用自相关函数法与改进虚假邻点法确定参数为:延时时间τ=10,嵌入维数m=13。邻域半径ε=8,Q=3。结果如图13所示。
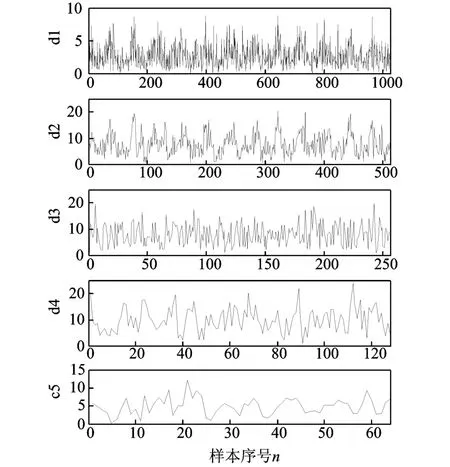
图12 双树复小波变换系数模Fig.12 The magnitude of the DT-CWT coefficients

图13 局部投影算法降噪Fig.13 Denoising result by local projective method
图13可见,经过局部投影算法处理后,与处理前相比d2的周期性被显著增强,随机噪声成分被有效地抑制。再对d2进行阈值为6.5的软阈值处理,还原为小波系数后进行双树复小波重构,便得到齿轮故障特性信号,如图14所示。
图14(a)为小波系数直接重构信号,(b)为系数降噪后重构所得信号,对比可知,双树复小波能够将信号中的周期性冲击成分提取出来,但是提取出的信号中依然包含较强的噪声,不利于故障特征的识别。对小波系数模进行局部投影算法与软阈值处理后,重构信号中的随机噪声被有效地抑制,信号中的周期性冲击成分已经非常明显。对降噪后的信号进行希尔伯特包络解调,便可以得到准确的齿轮故障特征频率76.17 Hz及其倍频,结果如图15所示。
图16为直接重构信号的希尔伯特包络解调谱,虽然也存在故障特征频率76.1 Hz及其3倍频228.5 Hz,但是存在169.9 Hz的干扰成分,而经过局部投影算法降噪后的信号中该成分已经被去除。

图14 重构信号对比Fig.14 Comparison of direct reconstruction signal and the one denoised by local projective method

图15 局部投影算法降噪信号希尔伯特包络谱Fig.15 Hilbert envelope spectrum of the signal denoised by local projective method before reconstruction
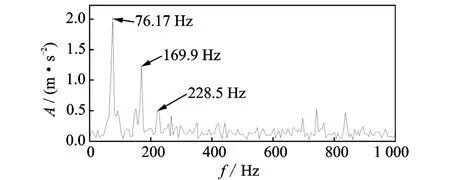
图16 直接重构信号包络解调谱Fig.16 Hilbert envelope spectrum of the direct reconstruction signal
综上,双树复小波变换与局部投影算法相结合,能够有效、准确地将齿轮早期故障信号中的故障特征信息提取出来。
6 结 论
本文研究了基于双树复小波与非线性时间序列局部投影算法的齿轮故障诊断方法,仿真分析与工程实践结果证明了该方法的可行性与有效性。
(1) 双树复小波变换的小波系数的模更能准确地反映信号中的周期性冲击成分。
(2) 非线性时间序列局部投影算法能够通过将序列扩展到高维相空间的方法,将特征信号与背景噪声分离。将其用于双树复小波系数模的周期性成分增强与降噪,具有显著效果。
(3) 双树复小波与非线性时间序列局部投影算法相结合的方法,能够从齿轮早期故障信号中准确有效地提取出故障特征信息,为齿轮的早期故障诊断提供了一种新方法。
[1]张超,陈建军,郭迅.基于EMD能量熵和支持向量机的齿轮故障诊断方法[J].振动与冲击,2010,29(10):216—220,261.Zhang Chao,Cheng Jianjun,Guo Xun.Agear fault diagnosis method based on EMD energy entrgy and SVM[J].Journal of Vibration and Shock,2010,29(10):216—220,261.
[2]Selesnick I W,Baraniuk R G,Kingsbury N G.The dual-tree complex wavelet transform[J].IEEE Digital Signal Processing Magazine,2005,22(6):123—151.
[3]Massimo Fierro,Ho-Gun Ha,Yeong-Ho Ha.Noise reduction based on partial-reference,dual-tree complex wavelet transform shrinkage[J].IEEE Transactions on Image Processing,2013,22(5):1 859—1 872.
[4]Turgay Celik,Tardi Tjahjadi.Image resolution enhancement using dual-tree complex wavelet transform[J].Geoscience and Remote Sensing Letters,IEEE,2010,7(3):554—557.
[5]王娜,郑德忠,刘永红.双树复小波包变换语音增强新算法[J].传感技术学报,2009,22(7):983—987.Wang Na,Zheng Dezhong,Liu Yonghong.New method for speech enhancement based on dual tree complex wavelet packet transform[J].Journal of Sensors and Actuators,2009,22(7):983—987.
[6]谢周敏,王恩福,张国宏,等.基于双树复小波包变换的地震信号分析方法[J].地震学报,2004,26(S1):110—115,175.Xie Zhoumin,Wang Enfu,Zhang Guohong,et al.Seismic signal analysis based on the dual-tree complex wavelet packet transform[J].Acta Seismologica Sinica,2004,26(S1):110—115,175.
[7]胥永刚,孟志鹏,陆明,等.双树复小波和奇异差分谱在滚动轴承故障诊断中的应用[J].振动工程学报,2013,26(6):965—973.Xu Yonggang,Meng Zhipeng,Lu Ming,et al.Application of dual-tree complex wavelet transform and singular value difference spectrumin the rolling bearing fault diagnosis[J].Journal of Vibration Engineering,2013,26(6):965—973.
[8]苏文胜,王奉涛,朱泓,等.双树复小波域隐Markov树模型降噪及在机械故障诊断中的应用[J].振动与冲击,2011,30(6):47—52.Su Wensheng,Wang Fengtao,Zhu Hong,et al.Denoising method based on hidden Markov tree model in dual tree complex wavelet domain and its application in mechanical fault diagnosis[J].Journal of Vibration and Shock,2011,30(6):47—52.
[9]邱爱中.对偶树复小波阈值降噪法及在机械故障诊断中的应用[J].机械传动,2011,35(9):58—61.Qiu Aizhong.Anew denoising method of DT-CWT and its application in mechanical fault diagnosis[J].Journal of Mechanical Transmission,2011,35(9):58—61.
[10]徐金梧,吕勇,王海峰.局部投影算法及其在非线性时间序列分析中的应用[J].机械工程学报,2003,39(9):146—150.Xu Jinwu,Lu Yong,Wang Haifeng.Local projective method and it′s application on nonlinear time siries[J].Chinese Journal of Mechinal Engineering,2003,39(9):146—150.
[11]王晨.基于非线性时间序列的胎儿心电信号分析与提取[D].北京:北京工业大学,2009.Wang Chen.Fetal electrocardiogram analysis and extraction based on nonlinear time series[D].Beijing:Beijing University of Technology,2009.
[12]任明荣,王晨,方滨,等.基于非线性时间序列的胎儿心电信号提取算法[J].系统仿真学报,2009,21(16):5 006—5 008.Ren Mingrong,Wang Chen,Fang Bin,et al.Fetal ECG extraction algorithm based on nonlinear time series[J].Journal of System Simulation,2009,21(16):5 006—5 008.
[13]吕勇,徐金梧,李友荣,等.基于局部投影和小波降噪的弱冲击特征信号的提取[J].北京科技大学学报,2004,26(3):319—321.LüYong,Xu Jinwu,Li Yongrong,et al.Weak Feature signals identification method based on local projective and wacelet transform[J].Journal of University of Science and Technology Beijing,2004,26(3):319—321.
[14]黄艳林,李友荣,肖涵,等.基于相空间重构与独立分量分析的局部独立投影降噪算法[J].振动与冲击,2011,30(1):33—36.Huang Yanlin,Li Yourong,Xiao Han,et al.Local independent projection de-noising algorithm based on phase-space reconstruction technique and independent component analysis[J].Journal of Vibration and Shock,2011,30(1):33—36.
Application of gear fault diagnosis method based on dual-tree complex wavelet transform and local projective method
XU Yong-gang,ZHAO Guo-liang,MAChao-yong,YANG Hong-yu
(Key Laboratory of Advanced Manufacturing Technology,Beijing University of Technology,Beijing 100124,China)
Asgear fault vibration signal is always nonlinear and nonstationary and always with a strong background noise which result in difficulty of fault feature extraction,a new method based on dual-tree complex wavelet transform and local projective method is proposed.As a improved method of the conventional discrete wavelet transform(DWT),dual-tree complex wavelet transform has many advantages over DWT,such as the improvement of frequency aliasing and oscillations of wavelet coefficients which is the key to the method proposed.Local projective method for nonlinear time series has a good ability of signal period strengthen and noise suppression,which fits for wavelet coefficients denoising.Firstly,the fault signal is decomposed by dual-tree complex wavelet transform to obtain the coefficients of different layers.Secondly,the nonlinear time series method is used to strengthen the periodicity of the coefficient whose amplitude is more periodic,and then do soft-threshold denoising.Finally,the fault characteristic signal can be obtained by coefficient reconstruction.The fault frequency can be located accurately by Hilbert envelope spectrum analysis.The simulation and engineering application showed the effectiveness of the method in early gear fault diagnose.
fault diagnose;dual-tree complex wavelet transform;local projective method;soft threshold;gear
TH165+.3;TH132.41
A
1004-4523(2015)04-0650-07
10.16385/j.cnki.issn.1004-4523.2015.04.019
胥永刚(1975—),男,副教授。电话:(010)67391750;E-mail:xyg@bjut.edu.cn
2014-04-10;
2014-09-03
国家自然科学基金资助项目(51375020);北京市教委科研计划资助项目(KM201310005013);北京市属高等学校青年拔尖人才培育计划资助项目;北京市优秀人才培养资助计划资助项目(2011D005015000006);北京工业大学基础研究基金资助项目
