空间多点人工地震动幅值收敛性研究

吴祚菊，张建经，王志佳，吴兴序，汪明元

(1.西南交通大学土木工程学院，四川成都610031；2.中国电建集团华东勘测设计研究院有限公司，浙江杭州310014)

空间多点人工地震动幅值收敛性研究

吴祚菊1，张建经1，王志佳1，吴兴序1，汪明元2

(1.西南交通大学土木工程学院，四川成都610031；2.中国电建集团华东勘测设计研究院有限公司，浙江杭州310014)

在空间相关性人工地震动生成中，计算的繁杂和局部场地收敛性与幅值收敛性之间存在的矛盾，是时域合成法中的两大主要问题。为了简化计算，同步实现局部场地及地震动幅值的双重收敛性，在对相位角分布进行深入研究的基础上，构建了空间多点人工地震动幅值收敛因子，并采用虚实分离法来分解功率谱矩阵。结果表明，该方法生成的多点人工地震动计算快速，且幅值稳定收敛。

地震动合成；空间相关；幅值收敛性；相位角分布；虚实分离法

引 言

在过去的几十年中，国内外学者提出了多种空间相关性人工地震动场的合成方法，这些方法主要可分为两类：时域调制法［1-4］，频域调制法［6-8］。其中，历经反复实践检验，理论体系较成熟而且应用最为广泛的是时域调制法，它采用窄频余弦信号双求和的级数形式作为空间地震动场的合成模型，模型中包含两个运动耦合系数和一个初始随机相位角，对耦合系数及随机相位角的求解即为空间相关人工地震动的生成的两个主要过程。

在时域调制法中，应用最早的是 Hao［1］的空间相关地震动模型，其他的都是在其研究基础上进行了改进。但在该模型的合成公式中，只考虑了研究质点之前一定影响范围之内各个质点的运动影响，而没有考虑研究质点之后所有质点的影响。

后来，屈铁军［2］对该传统时域合成方法进行了改进，认为空间研究质点不仅受到其之前所有质点的影响，还受到其之后的所有质点的运动耦合影响，在思维上有了很大突破，但由于其在对功率谱矩阵分解时采用了cholesky分解法，没能使这一想法真正得以实现(因为cholesky分解法只能将互功率谱密度矩阵分解为两个三角阵，当取上三角阵时，下三角区的元素全部为0，当其参与矩阵运算时，会失去研究质点之后所有质点的运动信息)。

为了使生成的人工地震动具有更好的空间相关性，真正能考虑到研究质点影响范围内所有质点的运动耦合，吴勇信［3］等采用了特征正交分解法来进行数学开方运算。用该方法将功率谱矩阵分解后，形成了两个共轭对称的Hermite矩阵，成功避免了cholesky分解法中因只能形成两个三角阵而会失去研究质点之后所有质点运动信息的缺陷，从而达到了真正的空间相关性。但是，由于该方法直接对复数矩阵(功率谱矩阵为复数矩阵)进行操作，分解时需要求得该复数矩阵的特征值和特征向量，因而计算过程较为复杂，计算效率不高，其应用和推广也因此受到了一定限制。

此后，董汝博［4］发现，以上3种地震动的合成模型中都存在一问题，那就是不具备局部场地的收敛性。因此，其在前人的研究基础上进行了改进，将初始随机相位角从一个双变量函数改成了单变量函数，从而达到了局部场地上的收敛性。但需要指出的是，当研究质点不断增多时，该模型会导致振幅的逐渐发散，最后无法收敛。针对以上存在的两方面问题，本文进行了如下改进：一方面，本文在该合成模型基础上，首次加入幅值收敛因子，使其在具有局部场地收敛性的同时，又具有地震动幅值的收敛性；另一方面，本文在吴勇信［3］的功率谱矩阵分解方法上进行了改进，首次将虚实分离法引入功率谱矩阵分解中，即先将功率谱矩阵进行虚实分离，分离后，只需求解一个实对称阵的特征值和特征向量，然后再将虚部添加，即可形成两个Hermite矩阵。这种方法避免了直接对复数矩阵进行分解，因此计算更为方便快速。

1 原始地震动模型

原始地震动模型采用窄频余弦信号双求和的级数形式，其中包含两个运动耦合系数和一个初始随机相位角，对耦合系数及随机相位角的求解即为空间相关人工地震动生成的两个主要过程，该模型具体如下［1-3］

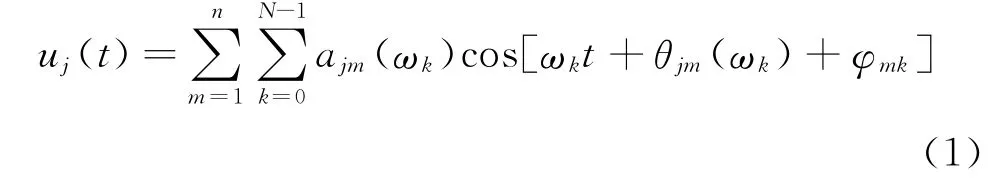
式中 ωk为圆频率(角速度)；t为时间变量；ajm(ωk)，θjm(ωk)为各质点间的运动耦合系数，它们分别表示当j质点为研究对象时，m质点的运动对j质点产生的幅值和相位的影响，当m从1变到n时，所有研究质点对j点的影响均能够考虑进去；φmk为初始随机相位角，m代表不同研究质点对初始随机相位角的影响，而k表示频率的变化对初始随机相位角的影响。

1.1 原始地震动模型的求解

1.1.1 建立功率谱矩阵

先采用第一点处的加速度峰值(PGA)，计算出第一点处的白噪声功率谱密度S0，然后按照往后各点与第一点间的土层厚度差Δh和震中距差Δx来修正S0，从而得到往后各点的白噪声功率谱密度。计算公式为

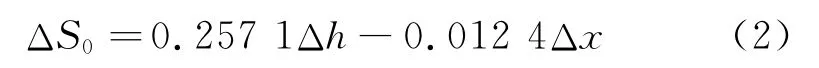
功率谱矩阵的主对角线元素为自功率谱模型，本文采用修正Kainan模型(Feng和Hu模型)。该模型的表达式为

其中：

式中 ω为功率谱模型的自变量，表示频率；ωg为场地的基频；ωc为低频截止频率；ξg为场地的阻尼；tmax为持时，var为调整参数。

功率谱矩阵主对角以外的元素为互功率谱密度函数，具体形式如下

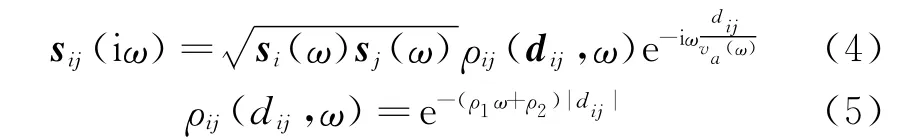
式中 ρ1，ρ2为待拟合参数；｜dij｜为两点之间的距离；dij为从j点到i点的矢量，有正负之分；si(ω)为i点处的自功率谱；sj(ω)为j点处的自功率谱；va(ω)为波从i点传到j点的平均视波速。

1.1.2 虚实分离法分解功率谱矩阵

为了计算快速方便，且具有真正意义上的空间相关性，本文首次采用虚实分离法来分解功率谱矩阵。其实现过程如下：

先将功率谱矩阵进行虚实分离

式中 Rnn(ωk)为实对称矩阵，很容易分解为Rnn(ωk)=PΛP-1，其中，P为Rnn(ωk)的特征向量矩阵，Λ为Rnn(ωk)的特征值矩阵；d1，d2，…，dn为各质点的坐标；vapp为相应计算点处的视波速。

求得P及Λ后，即可得矩阵的开方分解矩阵为

这里，Unn(iωk)即为所求的功率谱分解后矩阵。

式中 Unn(iωk)=UHnn(iωk)，H表示共轭转置。

1.1.3 利用分解功率谱矩阵求解耦合系数

改为经过本文的1.1.1与1.1.2节的计算后，获得功率谱矩阵sij(iω)，并开方分解得到一个共轭阵UHnn(iωk)，假设矩阵中第j行，第m列的元素为Ujm(iωk)，根据Ujm(iωk)与式(1)中运动耦合系数ajm，θjm的关系［2-4］，便可求解出式(1)中的运动耦合系数。其具体关系式如下：

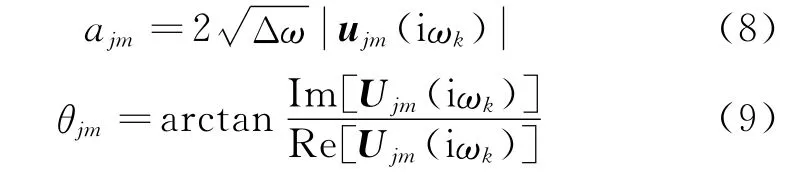
1.2 原始模型中各参数的取值

原始地震动模型的各参数取值如下：

①自功率谱中各参数的取值［3］：ωg=10 rad/s，ωc=1.8 rad/s，ξg=0.5，tmax=25 s。

②白噪声功率谱强度参数取值［3］：Ω=21.963 rad/s，var=125.529，PGA=0.18g。

③相关函数中的ρ1，ρ2按Feng和Hu模型［17］取值：

ρ1=2×10-5s/m，ρ2=88×10-51/m，va(ω)=130～350 m/s，vapp=130～350 m/s。

1.3 原始地震动模型的特点

该模型的特点是：当研究质点不断增多时，地震动时程的幅值可以稳定收敛；但是，当两个研究质点的水平距离逐渐趋于0时，两列地震动时程的相位不能趋于一致。为了详细说明这一特性，本文构造了一个由3个质点构成的平面布置模型，具体形式如下：

图1 各研究质点平面布置图Fig.1 The arrangement plan of each study particle

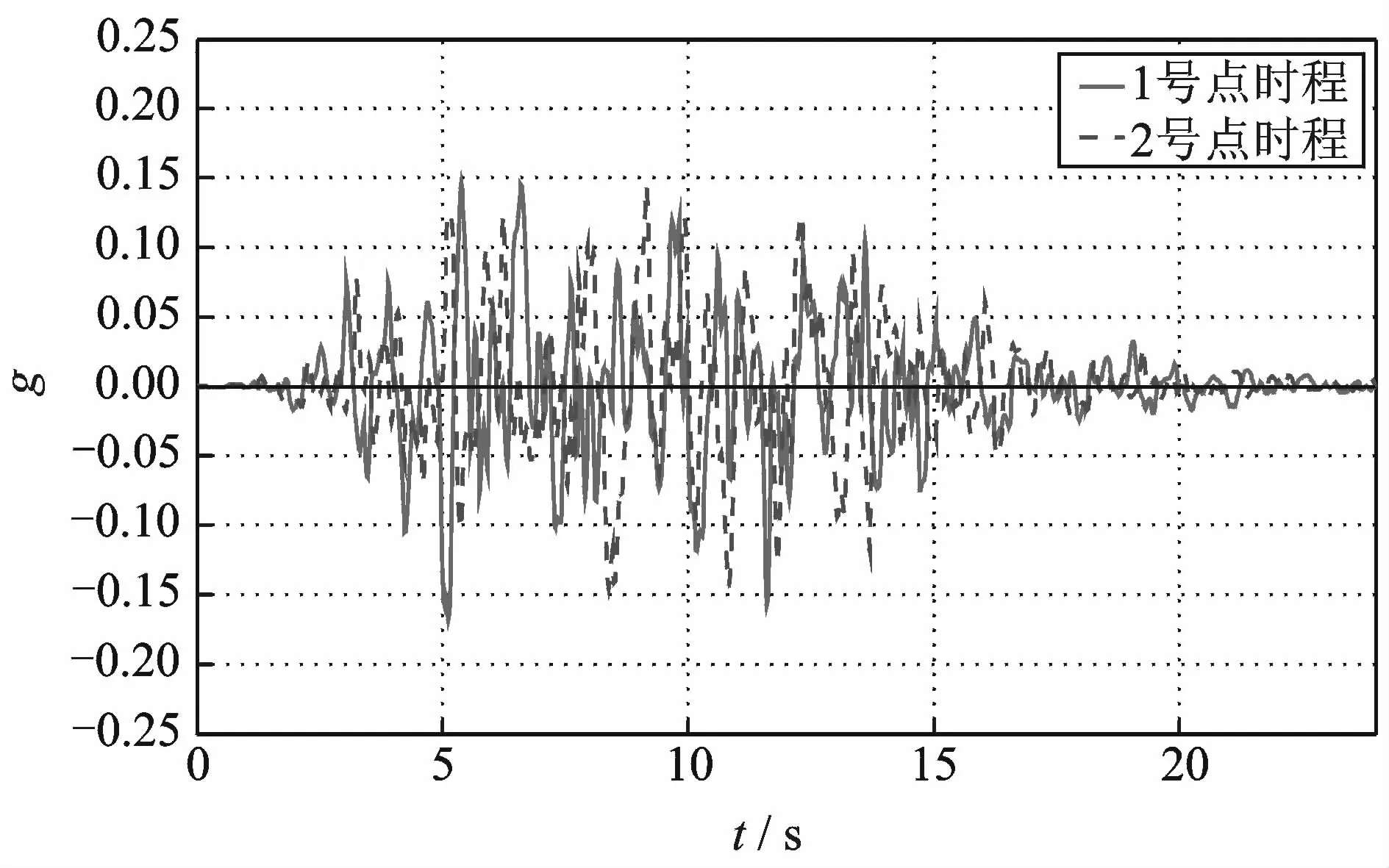
图2 1，2号质点时程曲线对比Fig.2 The time history curve contrast between point 1 and point 2

图3 1，3号质点时程曲线对比Fig.3 The time history curve contrast between point 1 and point 3

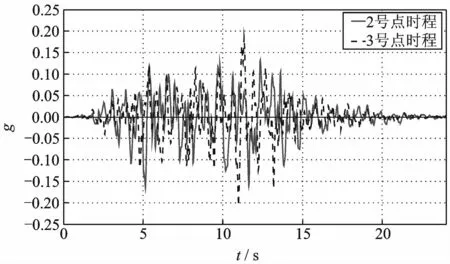
图4 2，3号质点时程曲线对比Fig.4 The time history curve contrast between point 2 and point 3

图1 中，地震波从左侧入射，其中1，2点相距较近(5 m)；2，3点相距较远(65 m)，在该模型下，生成的人工地震动时程如图2～4所示。距离计算之前，通常先对时间序列数据进行预处理，使得处理后的数据信息不仅能进行数据降维，而且还要保证近似的准确性。因此，PA-TWD法相对于传统的DTW法而言，能够大大减小计算的时间，有利于大规模时间序列的数据挖掘。该方法的基本

为了研究以上3个质点地震动波型的相似性，以及各波型的相似性与各质点间间距是否存在对应关系的问题，本文采取了分段聚合时间弯曲距离(PA-TWD)计算法［5］。该方法是在动态时间弯曲法(DTW)的基础上发展起来的，其在进行时间弯曲思想是：首先对各个时间序列进行PA计算，得到以时序段平均值为元素的特征序列；然后对这些序列进行时间弯曲距离计算。

假设有时间序列Q={q1，q2，…，qm｝和C={c1，c2，…，cn｝，按分段聚合时间弯曲法分别把它们平均分成ωq和ωc个时序段，并且计算各个时序段的特征，分别可以得到两个特征序列Q'={q'1，q'2，…，q'm｝和C'={c'1，c'2，…，c'n｝。再根据特征序列Q'和C'的元素值建立元素距离累计矩阵R，最终可以得到两个时间序列的距离度量LDTW(Q，C)=r( m，n)。

计算后具体结果如下列表1所示。

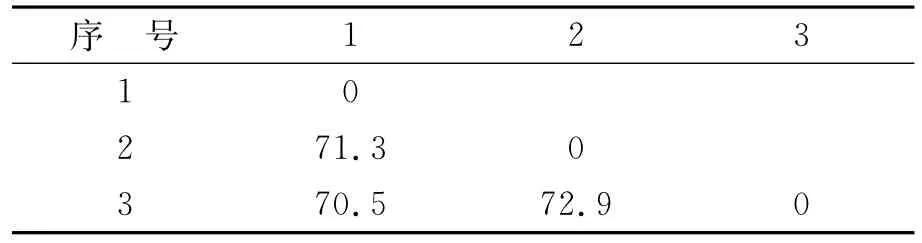
表1 各点间的PA_TWD计算Tab.1 The calculation of PA_TWD between any two points

从以上列表中可见，各质点间距离的远近与动态时间弯曲距离的计算值无明显的对应关系。比如，1，2点之间的距离只有5 m，其PA-TWD值(动态时间弯曲距离)为71.3；1，3点之间的距离为70 m，但PA-TWD值(动态时间弯曲距离)却只有70.3，反而比1，2点之间的PA-TWD值(动态时间弯曲距离)小。因此，从PA-TWD值随两点间距离的变化趋势来看，当两点之间的距离无限接近时，PA-TWD计算值不能趋近于0，即此时不能满足真实地震动中应有的特性(两列空间相关地震动时程在质点间距离无限小时应有的无限相似性)。

2 本文中生成的人工地震动时程

2.1 本文中功率谱矩阵分解方法的改进

在本文的人工地震动生成时，如本文中1.1.2节中所述，采用了虚实分离法分解功率谱矩阵，即先将功率谱矩阵进行虚实分离，然后再用特征正交法分解一个纯实数矩阵。因此避免了传统方法［3］中直接分解一个复数矩阵时计算繁杂、费时费力的缺点。文中方法仅需对一个实对称阵进行分解，因而其计算极为快速、简便。另外，在功率谱矩阵虚实分离后，本文采用特征正交分解法对分离出来的实对称阵进行分解，与传统的cholesky分解相比，其具有物理意义明确、空间相关性强等多方面的优点。因为，当对功率谱矩阵作cholesky分解时，分解后只能形成两个三角矩阵，在三角阵中，对角线之外另一半元素的缺失会使得研究质点之后所有质点的运动信息全部丢失，因而难以达到真正的空间相关性。当采用特征正交分解，分解后会生成两个完全非零的满秩矩阵，因而可以考虑研究质点影响范围内所有质点的运动耦合，从而达到真正意义上的空间相关性。

2.2 本文对初始随机相位角的研究

如式(1)中所示，传统的初始随机相位角的表达式为φmk，但从图2～4的研究结果可以看出，该双变量函数构成的人工地震动模型不具备局部场地的收敛性。因此，本文将φmk修正为φk，认为初始随机相位角只随频率ωk的变化而变化，其随不同耦合质点m的变化已在耦合系数θjm(ωk)中了进行修 正［4］。

初始随机相位角修正以后，本文中人工地震动场的局部场地收敛性如图5～7所示。

图5 修正后的1，2号点时程曲线对比Fig.5 The time history curve contrast between point 1 and point 2 in the modified model

图6 修正后的1，3号点时程曲线对比Fig.6 The time history curve contrast between point 1 and point 3 in the modified model

采用修正的模型后，从以上的3幅图形中，不用进行动态时间弯曲度的计算，便能直观地看出：虽然地震动时程曲线的整体幅值有所增大，但相位的一致性极好，而且，当两个点的距离无限接近时，从图5中可以看出，该模型基本能够达到局部场地的完全收敛。该研究结论与文献［4］的观点一致性较好。

图7 修正后的2，3号点时程曲线对比Fig.7 The time history curve contrast between point 2 and point 3 in the modified model

2.3 本文对幅值收敛性的研究

在以上研究过程中，虽然相位一致性较好，基本达到了局部场地的收敛性，但需要指出的是，这种方法生成的人工地震动幅值具有发散性。即随着研究质点的逐渐增多，同一质点的地震动幅值会逐渐发散，最终不能够收敛。下面以某一固定质点(质点A)的地震动加速度时程为例，将同一段100 m长的场地分别按等间距划分为6个质点、11个质点，41个质点等3种情况，具体划分如下：

图8 研究质点的划分数目及 A点布置图Fig.8 the plane of all particles division and the arrangement of point A

按照以上3种划分情况，当初始随机相位角满足两种不同的常用分布［12-14］(均匀分布及对数正态分布)时，其幅值的敛散性如图9，10所示。

2.3.1 当初始随机相位角呈独立于频率的均匀分布时

当初始随机相位角呈独立于频率的均匀分布时，随着研究质点从6个增加到41个，同一质点的地震动幅值会逐渐发散，且发散趋势较大，其具体情况如下图9所示。

图9 3种不同情况下A点的地震动加速度时程对比Fig.9 The acceleration time history contrast of point Ain the three different cases

2.3.2 初始随机相位角呈对数正态分布时

当初始随机相位角呈对数正态分布时，随着研究质点从6个增加到41个，同一质点的地震动幅值会随研究质点的增多而逐渐发散，其具体情况如下图10所示。

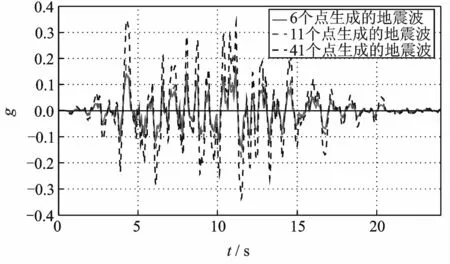
图10 3种不同情况下A点的地震动加速度时程对比Fig.10 The acceleration time history contrast of point Ain the three different dcases

从图9，10可以看出，无论采用哪一种单纯的相位分布时，修正模型在满足相位一致性较好的同时，都存在幅值发散现象，即随着研究质点从6个到41个，同一质点的地震动幅值会逐渐发散。

因此，为了解决以上问题，根据真实地震动中存在的能量非均匀分布及其逐步衰减原理，本文依据指数函数及幂函数的衰减性质，经过数千次参数试算后，构建出一个由常数项、幂函数项以及指数函数项等组成的幅值收敛因子，具体形式如下

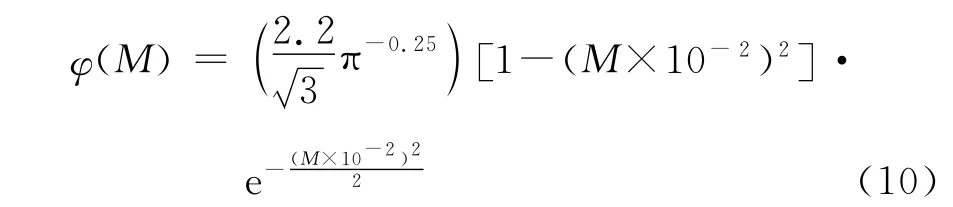
式中 M为研究质点的个数。从以上式子可以看出，随着M的增大，该收敛因子的函数值逐渐减小，呈现出与M相适应的衰减性。正是以上构造函数的这种性质，使得修正后的地震动模型具有幅值的稳定收敛性，其幅值不会随着研究质点的增多而逐步发散。

2.4 本文的人工地震动生成模型

经过以上功率谱矩阵分解方法的改进，传统模型中初始随机相位角的调整，以及在此基础上构建了幅值收敛因子后，本文的人工地震动生成模型如下

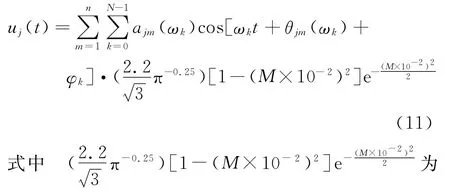
幅值收敛因子；ωk为圆频率(角速度)；t为时间变量；ajm(ωk)，θjm(ωk)为各质点间的运动耦合系数，它们分别表示当j质点为研究对象时，m质点的运动对j质点产生的幅值和相位的影响；φk为初始随机相位角。

2.5 该模型的幅值收敛性验证

相位角向量的取值一般有两种形式：一种认为相位角呈独立于频率的均匀分布［1-2］，即相位角的分布不受频率变化的影响，其作为一个独立的变量在［0～2π］上满足均匀分布；另一种形式则认为虽然相位角随频率的变化没有明显的分布规律，但其相位差谱随频率变化呈一定的分布关系，常用的相位差谱分布有对数正态分布、beta分布［9-13］等等。但需要说明的是，在一次实际的天然地震动中，相位差谱随频率的分布十分复杂，往往不能满足于某一种单纯的随机分布。因此，为了充分验证本文中修正后模型的幅值收敛性，除了以上的两种形式外，本文还增加了第3种情况的相位分布关系，即对从天然地震动中直接提取出相位角的情况也进行了验证。具体情况分类如下：

2.5.1 当初始随机相位角呈独立于频率的均匀分布时

当初始随机相位角的分布满足于独立于频率在［0～2π］上均匀分布时，随着研究质点的增多，由6个增加到41个，其幅值稳定收敛，具体情况如图11所示。

图11 3种不同情况下A点的地震动加速度时程对比Fig.11 The acceleration time history contrast of point Ain the three different cases

2.5.2 初始随机相位角的相位差谱呈对数正态分布时

当初始随机相位角的取值由相位差谱的对数正态分布决定时，其幅值收敛情况随着研究质点的增多，由6个增加到41个，其幅值稳定收敛，具体情况如图12所示。

图12 3种不同情况下A点的地震动加速度时程对比Fig.12 The acceleration time history contrast of point Ain the three different cases

2.5.3 从天然地震动中提取初始随机相位角时

该方法是有条件模拟［15-16］中采用的，一种从天然地震动中提取相位信息的方法，即直接从一次天然的地震记录中提取一条信息。本文中，为了解决直接获取多条空间相关性地震记录的困难(要求各地震记录台站的距离非常近)，本文利用行波效应因子来计算任意两个研究质点之间的迟滞相位角，再根据各迟滞相位角的空间相关性来形成相位角矩阵，从而衍生出多个相位角向量。具体过程如下：

(1)相位角信息的提取

首先，选取一条比较典型的天然地震动加速度时程记录，然后根据研究需要确定时间步长Δt，再根据该天然地震记录的总持时和时间步长Δt确定傅立叶变换阶数N；按1/Δt的采样频率对原地震记录进行采样，这样，便得到N个点的加速度时程信息；最后，将这N个点的信息作N阶FFT变换(快速傅立叶变换)，便可得到一个长度为N的相位角向量。这里，FFT变换阶数和信息采样点的个数是相等的。其中，FFT的变换公式中每个相位角对应的频率值计算，以及时间步长与步长之间的关系如下：

计算傅立叶谱的FFT公式为

式中 am(tk)为选取的天然地震动时程曲线，tk为时间离散值，N为傅立叶变换阶数。

相位角向量φ(ωj)的提取计算式为

式中 Im表示求虚部，Re表示求实部。频率及其步长的求法

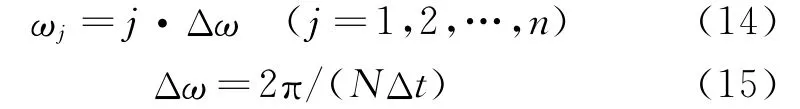
式中 ωj表示相位角向量中第j个相位值对应的频率，Δω为频率步长。

(2)相位角信息的繁衍及其矩阵的形成

由于各研究质点与震源距离的不同，因而地震波到达各个质点的时间会存在一个微小的差异，这个差异则称为行波效应。由于行波效应的存在，使得每个研究质点开始振动时的初始相位角各不相同，但与此同时，它们又满足一定的相关性。为了模拟这种在各个研究质点之间存在的空间相关性，本文首次引入了行波效应因子，来计算任意两个空间相关质点之间存在的迟滞相位，从而形成了一个n×n式的迟滞相位矩阵，其形式为

如前所述，式(17)等号右侧部分为行波效应体现因子，其中各变量的意义如前所述。其中，θmr(ωj)表示式(16)矩阵中第m行第r列所对应的元素(r=1，2，…，n；m=1，2，…，n)；其物理意义为，当研究m质点的相位角生成时，其他任意质点r的运动对m质点在窄频带ωj处产生的相位影响。

3 结论与展望

本文在现有研究基础上，对人工地震动合成原理进行了详细分析，在现有的合成模型上了进行初始随机相位角修正，首次构建出幅值收敛因子来对人工地震动的幅值进行调整，从而，使得该空间相关性人工地震动在局部场地收敛的同时，具备了完整的幅值收敛性。

图13 3种不同情况下A点的地震动加速度时程对比Fig.13 The acceleration time history contrast of point Ain the three different cases

但是，文中生成的人工地震动是通过先修正相位(董的模型)，再进行幅值修正(本文的模型)，虽然最终达到了相位一致，幅值收敛的效果，但幅值与相位的总体协调性还有待于进一步研究。目前，相位及相位差谱的研究还处于初级阶段，通过只修正相位或相位差谱的某种分布(无需进行幅值调整)，来生成具有局部场地及地震动幅值同步收敛的空间相关性人工地震动场，将会成为一个很好的研究方向。

［1］Hao'H，Oliveira C S，Penzien J.Multiple-station ground motion processing and simulation based on SMART-1 array data［J］.Nuclear Engineering and Design，1989，111：293—310.

［2］屈铁军，王前信.空间相关的多点地震动合成(I)基本公式［J］.地震工程与工程振动，1998，18(1)：8—15.Qu Tiejun，Wang Qianxin.Simulation of spatial correlative time histories of multi-point ground motion，part1：Fundamental formulas［J］.Earthquake Engineering and Engineering Vibration，1998，18(1)：8—15.

［3］吴勇信，高玉峰.基于功率谱矩阵开方分解的空间相关多点地震动合成方法［J］.工程力学，2012，29(4)：29—35.Wu Yongxin，Gao Yufeng.Simulation of spatial correlative ground motions based on the square root operation of power spectrum matrix［J］.Engineering Mechanics，2012，29(4)：29—35.

［4］董汝博，周晶，冯新.一种考虑局部场地收敛性的多点地震动合成方法［J］.振动与冲击，2007，26(4)：5—9.Dong Rubo，Zhou Jing，Feng Xin.Alocal convergent method for simulating multi-point earthquake ground motion［J］.Journal of Vibration and Shock，2007，26(4)：5—9.

［5］李海林，郭崇慧，杨丽彬.基于分段聚合时间弯曲距离的时间序列挖掘［J］.山东大学学报(工学版)，2011，41(5)：57—62.Li Hailin，Guo Conghui，Yang Libin.Time series mining based on piecewise aggregate time warping distance［J］.Journal of Shandong University(Engineering Science)，2011，41(5)：57—62.

［6］Thráinsson H，Kiremidjian AS.Simulation of digital earthquake accelerograms using the inverse discrete Fourier transform［J］.Earthquake Engineering and Structural Dynamics，2002，31：2 023—2 048.

［7］Rezaeian Sanaz.Simulation of orthogonal horizontal ground motion components for specified earthquake and site characteristics［J］.Earthquake Engineering and Structural Dynamics，2012，41(2)：335—353.

［8］田玉基，杨庆山.基于相位差谱的空间相关非平稳地震动场的模拟［J］.计算力学学报，2010，27(5)：828—833.Tian Yuji，Yang Qingshan.Phase-difference-based simulation of spatial correlated and non-stationary seismic ground motions［J］.Chinese Journal of Computational Mechanics，2010，27(5)：828—833.

［9］Boore D M.Phase derivatives and simulation of strong ground motions［J］.Bulletin of the Seismological Society of America，2003，93(3)：1 132—1 143.

［10］Nigam N C.Phase properties of a class of random process［J］.Earthquake-Engineering and Structural Dynamics，1982，11(10)：711—717.

［11］Shrikhande M，Gupta V K.On the characterization of the phase spectrum for strong motion synthesis［J］.Journal of Earthquake Engineering，2001，5(4)：465—482.

［12］Ohsaki Y.On the significance of phase content in earthquake ground motion［J］.Earthquake Engineering and Structural Dynamics，1979，7：427—439.

［13］朱昱，冯启民.相位差谱的分布特征和人造地震动［J］.地震工程与工程振动，1992，12(1)：37—44.Zhu Yu，Feng Qimin.Distribution characteristic of phase difference spectrum and artificial accelerogram［J］.Earthquake Engineering and Engineering Dynamic，1992，12(1)：37—44.

［14］Yokoyama T，Theofanopoulos N，Watabe M.Distribution of phase differences in relation to the earthquake magnitude，distance to the fault and local soil conditions［A］Proceedings of Ninth World Conference on Earthquake Engineering［C］.Tokyo-Kyoto，1988：813—818.

［15］Heredia-Zavoni，Eruesto，Fenton，et al.Conditional simulation of spatially correlated earthquake ground motion Vanmarcke［J］.Journal of Engineering Mechanics，1993，119(11)：2 332—2 352.

［16］Fenton，Gordon A.Conditioned simulation of local fields of earthquake ground motion［J］.Structural Safety，1991，(10)：247—264.

［17］Feng Q M，Hu Y X.Spatial correlation of earthquake motion and its effect on structural response［A］.Proceeding USPRC Bilateral Workshop on Earthquake Engineering［C］.1982，1：A-5-1—A-5-14.

The amplitude convergence study of artificial ground motions about special multi-points

WU Zuo-ju1，ZHANG Jian-jing1，WANG Zhi-jia1，WU Xing-xu1，WANG Ming-yuan2
(1.School of Civil Engineering，Southwest Jiaotong University，Chengdu 610031，China；2.Power China Huadong Engineering Corporation Limited，Hangzhou 310014，China)

In the generation of spatial correlation ground motion，there are two major problems in the time domain method，the complexity of calculation and the contradiction between local convergence and amplitude convergence.In order to simplify the calculation and realize the double convergence，on the foundation of further research about initial random phases，an amplitude convergence factor had been introduced to this paper for the first time.In addition to this，a new method had been introduced to decompose the power spectrum matrix，which separated the imaginary part from the real component.The results show that，with this method，the calculation is faster and the amplitude convergence is stable.

generation of ground motion；spatial correlative；amplitude convergence；phase distribution；method of separating imaginary part from a plural matrix

P315.9

A

1004-4523(2015)04-0610-08

10.16385/j.cnki.issn.1004-4523.2015.04.014

吴祚菊(1978—)，女，博士研究生，高级工程师，国家一级注册结构工程师，国家一级注册土木(岩土)工程师。电话：15928467027；E-mail：wuzuoju1234@163.com

2014-10-08；

2015-04-28

国家自然基金重大研究计划(41030742)；国防基础科研计划(B0220133003)；中国水电顾问集团公司重大科技项目资助：海上风电工程地质勘测关键技术研究(GW-KJ-2011-18)