频域分解模态识别方法的阻尼识别精度研究

杭 晓晨，蒋 令 闻，顾明 华，吴 邵 庆，费庆 国

(1.江苏省工程力学分析重点实验室，江苏南京210096；2.东南大学工程力学系，江苏南京210096；3.中国航空工业集团公司中航飞机研发中心，陕西西安710089)

频域分解模态识别方法的阻尼识别精度研究

杭 晓晨1，2，蒋 令 闻1，2，顾明 华3，吴 邵 庆1，2，费庆 国1，2

(1.江苏省工程力学分析重点实验室，江苏南京210096；2.东南大学工程力学系，江苏南京210096；3.中国航空工业集团公司中航飞机研发中心，陕西西安710089)

在模态参数识别中，模态阻尼比往往比固有频率、振型参数更难被准确识别。为了提高频域分解模态识别方法的阻尼识别精度，分析了算法中产生误差的主要因素，提出了采用自回归模型谱估计代替原有周期图谱估计的改进方法。开展了仿真算例研究，以白噪声激励下结构的振动响应为输入条件，使用频域空间域分解法进行模态参数识别。算例结果验证了采用基于自回归模型的谱估计代替原有的周期图法谱估计，既保留了对密频模态的分辨能力，又提高了阻尼参数的识别精度，且在采样数据长度较短的情况下具有优越性。

参数识别；阻尼识别；频域分解法；谱估计

引 言

频域分解(Frequency Domain Decomposition，FDD)类方法是一类运行模态分析［1］(Operational Modal Analysis，OMA)方法，通过测量结构在环境激励下的振动响应，得到能够反映真实动力学特性的模态参数。在模态参数中，阻尼比往往会比固有频率、振型更难被准确识别［2-4］。因此有必要对此类方法的阻尼识别精度展开研究，分析阻尼识别误差的来源，改善识别效果。FDD方法最早由Brincker等在复模态指示函数的基础上提出［5］，在满足白噪声激励假设和小阻尼假设时，能够很好地识别模态频率和振型，且对密集模态的分辨率较高，但存在无法识别模态阻 尼的缺 点［6］；为 了解决 这一问 题，Brincker等随后提出了增强频域分解法［7］(Enhance Frequency Domain Decomposition，EFDD)，在FDD的基础上将频域信息转化到时域，然后在时域中使用对数衰减(Logarithmic Decrement，Logdec)法得到模态阻尼比。然而EFDD方法在时-频域转化的过程中必然带来数据截断，造成了阻尼识别的不精确；王彤等［8］提出频域空间域分解法(Frequency and Spatial Domain Decomposition，FSDD)，引入增强功率谱密度(Enhance Power Spectrum Destiny，EPSD)的概念，直接在频域内对EPSD进行最小二乘拟合后获得模态频率和阻尼。Zhang等［9］利用FSDD法实现了对几个实际工程结构的模态识别。

总的来说，FDD类方法使用奇异值分解［10］(Singular Value Decomposition，SVD)技术，将信号空间与噪声空间分离开来，抗噪声干扰能力较强，且具有较好的密频分辨能力。本文重点关注FDD类方法的阻尼识别精度问题，首先从算法上分析带来误差的几个因素，并针对其中影响较大的可控因素——功率谱估计方法进行探讨，提出使用基于自回归(Autoregressive，AR)模型的谱估计方法进行改进，开展了两个仿真算例验证，得到了一些结论。

1 频域分解模态识别方法的理论分析

FDD类方法都是基于如下的输入、输出功率谱密度函数(Power Spectrum Destiny，PSD)关系

式中 Gxx(jω)，Gyy(jω)分别为输入和输出PSD矩阵；H(jω)为频响函数(Frequency Response Function，FRF)矩阵，FRF可以用部分分式形式表示式中 N为模态阶数，λr为第r阶极点，Rr为第r阶留数矩阵，R*r为第r阶模态振型与模态参与向量转置的乘积，即Rr=φrγTr。假设输入为一白噪声，则Gxx(jω)为一实常数对角阵，将式(2)代入到式(1)，化简得到

式中 Ar为相关的留数项，在小阻尼情况下，r阶模态附近Ar可以被简化为

式中 dr=Cγr为一实数。在某一频率处，当只有少数几个模态(一般只有一个或两个)贡献显著时，定义这些模态集合为Sub(ω) ，响应PSD矩阵可以写成

式中 Ui为奇异值向量矩阵，Si为奇异值组成的对角矩阵。

在输出的PSD图中，如果谱峰附近仅有第r阶模态起主导作用，那么方程(5)可以近似为

对比式(6)和(7)，第一个奇异值向量ur即为第r阶模态振型，对应的奇异值具有单自由度特性，通过比较奇异值曲线峰值附近模态振型的模态置信度(Modal Assurance Criterion，MAC)确定此单自由度特性曲线的范围，进而确定固有频率。

EFDD法是FDD法的改进方法，它解决了FDD法无法识别阻尼参数的问题。EFDD选取了奇异值曲线峰值附近MAC值较大的频段，对其作逆傅立叶变换运算(Inverse Fast Fourier Transform，IFFT)转换到时域，获得了近似的单自由度相关函数曲线，然后用对数衰减法识别模态频率和阻尼。然而，EFDD法使用IFFT时会使数据截断，得到的相关函数是不精确的，导致阻尼识别产生偏度误差。

FSDD法直接在频域中识别模态参数，因此避免了对奇异值曲线作IFFT带来的误差。将奇异值曲线作为指示函数，并定义第r阶模态的增强PSD

联系式(7)，在第r阶模态主导的谱峰附近窄带，EPSD具单自由度特性，且

用最小二乘法拟合此EPSD曲线，求出极点λr，进而得到模态频率和阻尼。

FDD类方法的基本原理可以概括为图1所示。分析以上3种方法的基本理论，可以得到FDD类方法参数识别的误差的来源：

1)输出PSD估计ˆGyy与真实PSD间存在误差。响应PSD估计作为FDD类识别算法的最初输入，对最终识别结果的影响较大；

2)使用激励白噪声假设以及小阻尼假设进行近似产生误差。这些假设是整个识别算法成立的前提，但在激励时间足够长，模态阻尼较小时，这些假设引起的误差可以忽略；

3)由单自由度特性曲线得到模态参数时的数值误差。EFDD法中IFFT运算、Logdec法均会产生此类误差。而FSDD直接在频域中进行识别，数值误差仅存在于最小二乘拟合过程中，当拟合数据较为平滑时，可以认为这种误差很小。

图1 FDD类方法基本流程图和误差分析Fig.1 Flowchart and error analysis of FDD methods

2 功率谱估计理论

FDD类方法均采用周期图(Periodogram)法来估计输出响应的PSD［5］。假设N点的离散输出响应信号为x(n) ，n=0，1，2，…，N-1，周期图法PSD估计［11］

周期图法PSD估计的均值

式中 W(ω)为数据截断时采用的窗函数w( n) 的频域描述。可见，周期图法PSD估计为真实谱S(ω)与窗谱W(ω) 的卷积，只有当N→∞时，E((ω))→S(ω) ，才是无偏估计。而实际情况N总是一个有限值，所以周期图法PSD估计与真实谱之间存在偏差

改进的周期图法对总数据进行有重叠分段，然后对每一段数据选用合适的窗函数以减少谱泄漏，最后对各分段估计PSD后进行平均。假设总数据量为N，分成L段，每段有M个数据，由于有数据重叠，N≠M×L，运算过程可以表示为：

改进的周期图法最大的优点在于减小方差，当N→∞时，Var→0，为渐进一致估计。总的来说，周期图谱估计方法具有较高的频域分辨率，但估计方差大，谱泄漏严重，其改进方法采用分段、加窗等措施，降低了频域分辨率，提高了估计效果，但在数据长度一定的条件下，依然不满足无偏性、一致性估计条件。FDD类方法以此PSD估计为基础，模态参数的识别精度不能保证。尤其是在颤振试飞试验等工程应用领域，由于试验条件限制，采样数据不可能很长，PSD估计误差愈加明显。

本文提出基于AR模型谱估计代替周期图谱估计的改进方法。AR模型谱估计是一种参数化模型估计方法，它不存在对离散序列进行时-频域转化的过程，避免了周期图法中存在的泄漏、方差等问题，在合适的模型阶数下，PSD估计效果更好［11］。AR模型可用如下差分方程表示

式中u( n) 是均值为零方差为σ2的白噪声序列；p为AR模型阶数；ak，k=1，2，…，p为对应的p阶模型参数。通过AR系统的传递函数 H( z) ，可以推得信号 x( n) 的PSD估计

可见基于AR模型的PSD估计关键在于求解模型参数。式(19)经过相关函数的变换可以得到Yule-Walker方程［12］

式中 r(p)为信号 x ( n) 的相关函数。求解Yule-Walker方程即可得到模型参数，Burg法［13］可以避免对离散信号进行自相关估计，因此本文之后的AR模型参数估计均使用Burg法。

3 算例研究

采用两个算例进行仿真研究，第1个为二自由度弹簧-振子系统，用于说明更换谱估计方法后能否保持FDD类方法对密频模态的识别能力；第2个为大展弦比机翼仿真模型，用于比较两种PSD估计方法对阻尼识别精度的影响。算例均采用FSDD法识别模态参数。

3.1 二自由度弹簧-振子模型

为了验证基于AR模型的PSD估计方法对密频模态的识别能力，建立如图2所示的两阶频率靠近的二自由度系统。m1=10 kg，m2=1.03 g，k1=1 000 k N/m，k2=100 N/m，通过模态叠加法确定两阶密频模态频率为f1=49.61 Hz，f2=50.40 Hz，c1和c2的取值使两阶模态阻尼比均为2%。

图2 二自由度弹簧-振子系统Fig.2 Two-DOFspring oscillator

在质量块m1上施加白噪声激励力，在m1，m2上采集振动位移响应。响应信号的采样频率fs=200 Hz，分别取N1=2 000和N2=10 000个采样点，来研究两种采样长度条件的识别。

取m2点输出响应为例，图3为使用AR模型和使用周期图法得到的PSD对比图。可见周期图法谱估计曲线不平滑，且第二阶模态峰不突出，幅值上已经失真。而基于AR模型估计的PSD曲线光滑，能够很好地分辨两阶峰。两种谱估计方法对应的奇异值曲线对比如图4所示。

图3 两种估计方法的响应PSD比较Fig.3 Comparison of two PSD estimations

模态参数识别结果如表1和2所示，经过分析可得：

1)虽然周期图法对响应信号的PSD估计效果较差，但经过FSDD识别后依然能够区分两阶密频模态，验证了 FDD类方法易于区分密频模态的优点。基于AR模型进行PSD估计，保留了较高的密频分辨率；

图4 奇异值曲线比较Fig.4 Comparison of two singular value plots

表1 采样数据N1=2 000时2种方法识别结果Tab.1 Identification results of the two methods when data length N1=2 000

表2 采样数据N2=10 000时2种方法识别结果Tab.2 Identification results of the two methods when data length N2=10 000

2)采用周期图法和AR模型PSD估计方法都能获得良好的频率识别精度。然而，在数据长度较短时，前者对阻尼的识别误差很大，后者阻尼识别精度较高。

3.2 大展弦比机翼模型

将一大展弦比机翼进行有限元建模，它的计算模态分析结果作为准确值。通过在有限元模型上施加随机激励，进行瞬态响应分析，提取时程响应数据，来模拟运行模态试验。最后对响应数据进行识别得到模态参数，与计算模态分析的结果进行对比验证。

机翼具体参数如表3所示，几何模型和有限元模型如图5所示，边界条件为根部固支，模态阻尼比设为2%。机翼有限元模型的前7阶模态分析结果如表4所示。

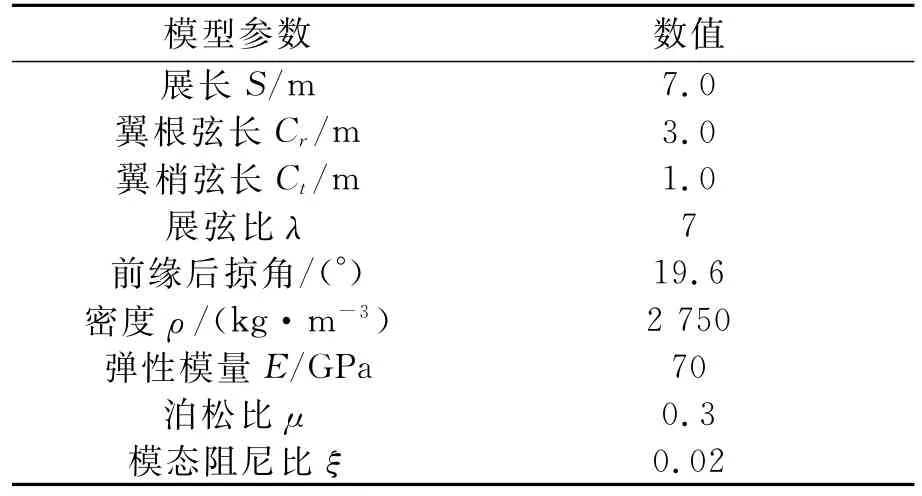
表3 大展弦比机翼模型参数Tab.3 Properties of the wing with high aspect ratio

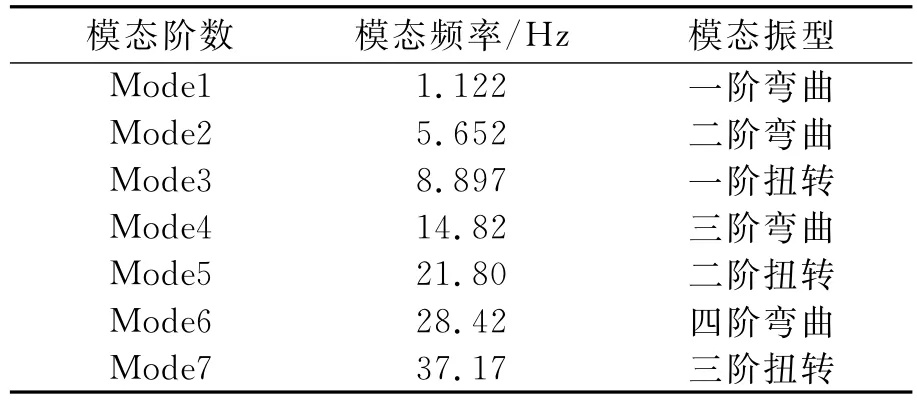
表4 有限元模型模态分析结果Tab.4 Modal analysis results of FEM

在机翼模型上进行多点的均值为零、方差为1的高斯白噪声激励，激励时间50 s。响应采集通道设置为沿机翼表面均匀分布的12个测点(如图5所示)，采样频率fs=200 Hz，采集时间取T1=20 s，T2=50 s，以便分析数据长度对识别结果的影响。

分别使用改进的周期图法、AR模型法进行输出谱的估计，固有频率的识别结果如表5所示，模态阻尼的识别结果如表6所示。

图5 大展弦比机翼的几何模型Fig.5 Geometry of the wing with high aspect ratio

表5 模态频率识别结果Tab.5 Identification results of modal frequencies

表6 模态阻尼识别结果Tab.6 Identification results of modal damping

分析表5和6数据可得到初步的结论：

1)两种方法对模态频率都具有良好识别精度，误差都在2%以内。而对于阻尼参数的识别，同数据长度条件下，基于AR模型的PSD估计方法识别效果更好；

2)周期图法在短数据阻尼识别精度不理想，增大数据强度可以提高识别精度，这是因为更大的数据长度能使周期图PSD估计趋向于无偏估计；

3)对于AR模型PSD估计方法来说，较短的输入数据(4 000个采样点)也能获得良好的阻尼识别精度。

由于作为激励的白噪声信号的产生具有随机性，一次仿真试验的结果往往不能说明结论的普遍性。因此重复进行了25次仿真，每次产生一组随机激励信号，响应数据点定为10 000个。取第三阶模态为例，只考虑识别其模态阻尼比，识别误差如图6所示。

由图6可知：采用周期图法谱估计，模态阻尼识别误差波动较大，最大误差可能超过10%；而采用基于AR模型的谱估计方法，模态阻尼的识别误差基本在5%以下，证明了采用自回归模型谱估计方法能获得更好的阻尼识别效果。

图6 第三阶模态阻尼识别误差Fig.6 Damping identification error of the third mode

4 结 论

本文分析了FDD类模态参数识别算法产生误差的主要因素，提出采用基于自回归模型的谱估计方法改进响应PSD的估计精度，进而提高模态识别精度，采用两自由度系统和大展弦比机翼进行了有限元仿真研究，主要结论如下：

1)功率谱作为FDD类方法的输入条件，其估计的准确性是影响模态参数识别精度主要因素。传统的周期图估计不满足估计的无偏性和一致性，尤其在短数据条件下，模态阻尼的识别精度难以保证；

2)使用基于AR模型的PSD估计方法代替周期图法，既保留了FDD类方法对密频模态的识别能力，又提高了模态阻尼的识别精度，且识别效果受数据长度影响不大。这是因为AR模型估计法避免了对离散信号进行时频域转换，不存在“谱泄漏”带来的偏度误差。但是参数化方法必须选取合适模型阶数p，本文通过对比周期图法得到的奇异值曲线，峰值位置相近时确定p的取值。这种方法类似于时域模态参数识别中常用的稳定图和频谱图联合定阶的方法［14］，具有较好的定阶效果；

3)对于颤振试飞试验等只能获得有限数据，但又对阻尼识别精度要求较高的情况，本文提出的基于谱估计改进的FDD类方法具很大的优越性。

［1］Reynders E.System identification methods for(operational)modal analysis：review and comparison［J］.Archives of Computational Methods in Engineering，2012，19(1)：51—124.

［2］Andrianne T，Dimitriadis G.Damping identification of lightly damped linear dynamic systems using commonbase proper orthogonal decomposition［J］.Mechanical Systems and Signal Processing，2012，28：492—506.

［3］Ding Y，Law S S.Structural damping identification based on an iterative regularization method［J］.Journal of Sound and Vibration，2011，330(10)：2 281—2 298.

［5］Brincker R，Zhang L，Andersen P.Modal identification from ambient responses using frequency domain decomposition［A］.Proceedings of 18th International Modal Analysis Conference［C］.2000：625—630.

［6］Zhang L.An overview of major developments and issues in modal identification［A］.Proc.IMAC XXII［C］.Detroit(USA)，2004：1—8.

［7］Brincker R，Ventura C，Andersen P.Damping estimation by frequency domain decomposition［A］.Proceedings of 19th International Modal Analysis Conference［C］.2001：698—703.

［8］王彤，张令弥.运行模态分析的频域空间域分解法及其应用［J］.航空学报，2006，27(1)：62—66.Wang T，Zhang L M.Frequency and spatial domaindecomposition for operational modal analysis and its application［J］.Acta Aeronautica Et Astronautica Sinica，2006，27(1)：62—66.

［9］Zhang L，Wang T，Tamura Y.Afrequency-spatial domain decomposition(FSDD)method for operational modal analysis［J］.Mechanical Systems and Signal Processing，2010，24(5)：1 227—1 239.

［10］Henry E R，Hofrichter J.Singular value decomposition：application to analysis of experimental data［J］.Essential Numerical Computer Methods，2010，210：81—138.

［11］Stoica P，Moses R L.Spectral Analysis of Signals［M］.Upper Saddle River，NJ：Pearson/Prentice Hall，2005.

［12］Marple L.Anew autoregressive spectrum analysis algorithm［J］.IEEE Trans.on Acoustics，Speech and Signal Processing，1980，ASSP-28(4)：441—454.

［13］Brockwell P J，Davis R A.Introduction to Time Series and Forecasting［M］.Springer Science&Business Media，2006.

［14］Rainieri C，Fabbrocino G.Automated output-only dynamic identification of civil engineering structures［J］.Mechanical Systems and Signal Processing，2010，24(3)：678—695.

Accuracy of modal damping identification using frequency domain decomposition method

HANG Xiao-chen1，2，JIANG Ling-wen1，2，GU Ming-hua3，WU Shao-qing1，2，FEI Qing-guo1，2
(1.Jiangsu Key Laboratory of Engineering Mechanics，Nanjing 210096，China；2.Department of Engineering Mechanics，Southeast University，Nanjing 210096，China；3.Research and Development Center of AVIC Aircraft Corporation，Ltd.，Aviation Industry Corporation of China，Xi'an 710089，China)

Modal damping ratios are more difficult to be accurately identified compared with nature frequencies and mode shapes in modal parameters identification.To improve accuracy of the damping identification using frequency domain decomposition method，an error analysis is conducted and a spectrum estimation method based on autoregressive model is presented instead of the previous periodogram method.Two simulation examples are implemented in which the measurement response data of structure under white noise excitation is adopted as input to identify the modal parameters using the frequency and spatial domain decomposition.Results indicate that with the proposed method the ability of distinguishing closely spaced modes is retained，and identified damping ratios can be more accurate.Moreover，the proposed method is superior to periodogram method when the sampling data is not long enough.

parameters identification；damping identification；FDD；spectral estimation

TB123；O329

A

1004-4523(2015)04-0518-08

10.16385/j.cnki.issn.1004-4523.2015.04.003

杭晓晨(1990—)，男，博士研究生。电话：(025)83790168；E-mail：hangxioachen@seu.edu.cn

2014-01-11；

：2014-06-17

国家自然科学基金资助项目(10902024)；教育部新世纪优秀人才支持计划资助项目(NCET-11-0086)；航空科学基金资助项目(20090869009)；江苏省普通高校研究生科研创新计划资助项目(CXZZ13_0084)