风力机非定常气动力降阶模型

郭 强，刘鹏寅，竺晓程

（1.上海汽车集团股份有限公司乘用车公司，上海201804；2.上海交通大学机械与动力工程学院，上海200240）

众所周知，准确的非定常气动力模型是风力机气弹设计的重要组成部分.而气弹的不稳定和颤振是风力机设计必须考虑的问题，因此准确预测风力机叶片所受动态气动载荷在风力机设计中尤为重要.由于整个设计流程是一个不断迭代的过程，因此所需的气弹计算模型不仅要准确而且要快速，尤其是对于气弹现象复杂的风力机叶片［1］.风力机叶片的非定常气动载荷主要是由于在自然环境中，大气紊流、塔架影响、地面边界层效应以及偏航工况等因素影响，使得风力机叶片处于非定常流动区域.在此情况下，叶素的有效攻角在不断变化，并会导致动态气动载荷的出现.

这一动态气动载荷的特征取决于边界层是附着还是分离.如果叶片表面流动是附着的，翼型所受的动态气动载荷与静态气动载荷差别不大，主要表现为一种延时现象.如果叶片表面流动出现分离，叶片振动将使得有效攻角呈非定常变化，同时导致动态失速的发生.在流动分离工况下，翼型的动态气动载荷和静态气动载荷会有相当大的区别，动态失速使叶片所受的最大气动载荷大大增加.而随着风力机直径的增大，过大的气动载荷增加了风力机稳定控制的难度.从稳定方面考虑，至少在升力预测时需要加入动态失速模型以减小预测误差［2］.

从非定常气动力预测精度来看，随着计算机技术的显著进步以及数值计算和湍流模型方面所取得的进展，通过CFD 方法来研究非定常气动力的动态响应变得越来越切实可行.大量这方面的工作［3-5］不仅对了解非定常气动力的变化发展有积极作用，同时也证明了CFD 方法在常规风力机和直升机桨叶设计中必会起到越来越重要的作用.但是较高精度的CFD 方法需要较高的计算成本.

因此，依靠少量数值计算算例结果建立预测模型，并对其他工况进行预测模拟的方法逐渐引起研究人员的兴趣.降阶模型方法是这类非定常气动力预测模拟方法中较常用的一种，常用的2种降阶模型有：ARMA 模型［6］和Volterra级数模型［7］.这类方法的主要优点是其精度可随着CFD 方法的改进而提升.当流动复杂程度增加时，基于高适用性的CFD 方法的降阶模型将比半经验模型更为可靠.

由于三维问题的复杂程度较高，笔者将风力机叶片的动态气动载荷问题简化为二维翼型进行振荡运动时的气动力变化.在附着流动和分离流动情况下，分别对翼型的升力系数采用2种不同降阶模型进行预测，并将预测结果与CFD 计算结果进行对比，以验证降阶模型的有效性.

1 CFD计算

采用带转捩修正的k-ωSST 湍流模型.图1为计算所用的网格和翼型表面附近的网格.采用三角形和四边形混合的网格，整个计算区域分为外部静止区域（简称外部区域）和内部围绕翼型振荡的运动区域（简称内部区域）.外部区域全部采用四边形网格，内部区域采用三角形和四边形混合网格.为了减小界面通量传递的插值误差，内、外区域交界面具有相同大小和数量的一致网格.翼型周围采用C 型四边形边界层网格，翼型表面网格节点总数为400.第一层网格的布置确保y＋在1.0量级处，且保证网格的法向膨胀率不大于1.1.外部进、出口边界位于距翼型约20倍弦长处.入口边界设置速度分量及合适的入流湍流度，出口边界为静压力边界，翼型表面的边界条件为振荡运动的无滑移壁面.经过时间步长无关性检查，采用的时间步长为0.001s，每个工况都至少经过5个连续周期的计算以得到周期性稳定的流场［4］.需要指出的是这样一个非定常工况的CFD 计算需要十几个小时，对于需要大量工况数据的设计和优化工作而言计算成本较高.

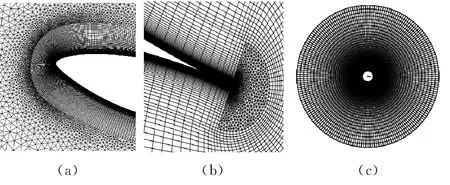
图1 计算网格Fig.1 Computational mesh

2 降阶模型

2.1 ARMA 模型

ARMA 模型将某时刻动态气动载荷的响应认为是当前时刻的动态输入和前几个时刻的动态输入与响应的线性组合.因此当前时刻的动态响应可以表示为：

式中：u（n）为动态输入，此处认为是n时刻的攻角；y（n）为非定常状态的动态气动载荷响应，在本文中响应y为升力系数；na和nb分别为可自定义的模型的阶数；ani和bni为待辨识的模型参数.

将式（1）以矩阵形式给出，可得到ARMA 模型的另一表达式：

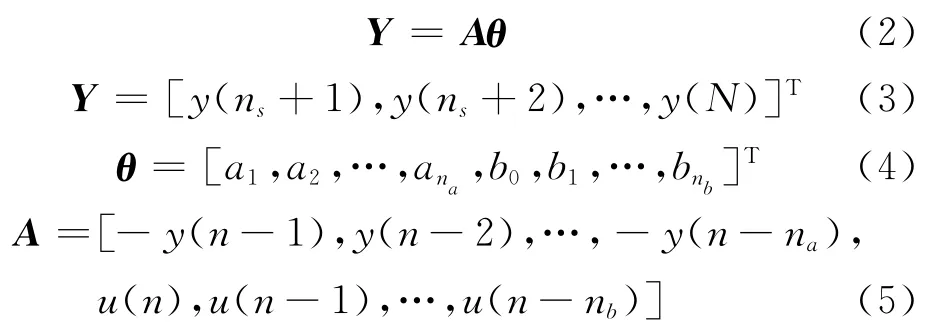
式中：n＝ns＋1，ns＋2，…，N；ns＝max［na，nb］；N为离散时间步的总数.

采用最小二乘法进行辨识，可以得到模型的未定参数：

通过以上方法提取一个工况算例的数据作为样本，通过辨识得到ARMA 模型的待定参数，从而建立ARMA 模型，并依靠建立的ARMA 模型对其他工况的动态响应进行预测.

2.2 Volterra级数模型

Volterra级数模型是较常用的非线性响应模型.对一个离散系统来说，输入响应可由式（7）表示：

式中：h0为稳态响应值；hi（n-k1，n-k2，…，n-ki）为第i阶Volterra核.

由于Volterra核随阶数的变化呈指数增长，求解高阶的Volterra核需要较高的计算资源确定，所以对于一个非线性系统，二阶或三阶Volterra级数是最常用的模型.笔者选用二阶Volterra级数模型.

设定一个记忆长度M，二阶的Volterra级数可以变化为

若将输入以矩阵形式表示：

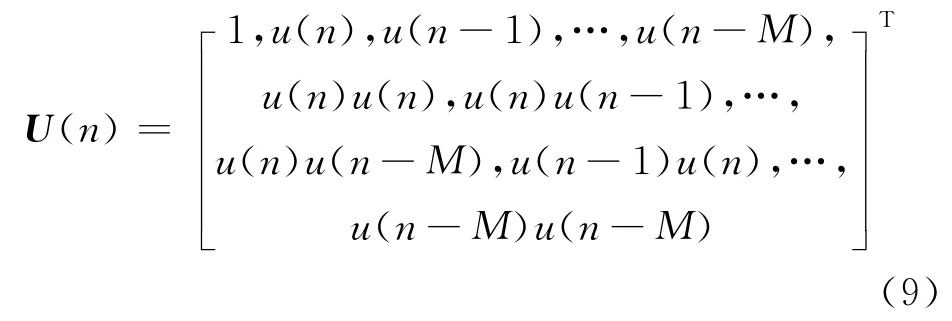
由此可以将二阶的Volterra级数模型改写为矩阵形式：

其中

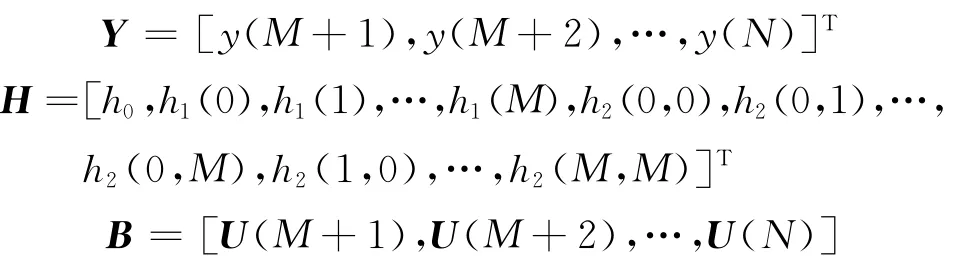
这样待辨识的模型参数就可由最小二乘法得到：

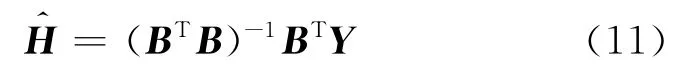
一旦辨识得到各阶Volterra核，就可以建立Volterra级数模型并预测非定常气动载荷.需要特别指出的是，以上2个模型的辨识所需时间在1～2 min内，而模型建立后预测某一工况结果所需的时间在几秒钟左右.

3 不同工况的降阶模型预测

采用S809翼型进行计算，其静态失速攻角在10°左右.该翼型的升力系数在失速攻角（最高值）附近保持一段较高的数值，而阻力系数在很大的攻角变化范围内较小.这些特性使得翼型在变工况下保持较好的气动特性.为了得到动态失速下的翼型非定常气动载荷，定义风力机翼型绕转轴（x／c＝0.25）周期振荡的变化形式为：

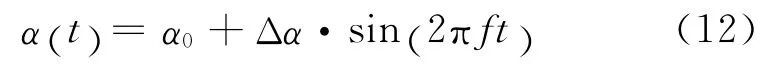
式中：α0为振荡的平均攻角；Δα为振荡的振幅；f为振荡频率.

同时定义衰减频率为

式中：c为弦长；U为来流速度.

衰减频率反映了沿翼型弦向的主流运动和绕转轴的振荡运动之间的相互作用，其值表征振荡运动对主流运动影响的大小，所以当给出振荡的平均攻角、振幅和衰减频率后，某一特定翼型的振荡变化就可以确定.

所有模型的辨识数据都是由CFD 数值计算得到的.对每个非定常气动计算结果，定义时间t0和tf为观测的初始和终止时刻.对一个周期内的数据进行处理后得到：

3.1 流动附着工况

将α0＝4°、k＝0.050和Δα＝2°工况下的CFD计算作为样本，根据式（6）建立ARMA 模型.由于更高的阶数已不能提高模型的精度，通过对比选取na＝2，nb＝1.当翼型在这一小攻角（远小于静态失速攻角）处振荡时，流动未发生分离，因此升力系数的变化十分平缓，非线性现象很轻微.这种情况下采用模拟弱非线性系统的ARMA 模型进行动态气动载荷的预测较有效.

图2给出了样本工况的升力系数随攻角变化的气动力迟滞回线.由图2可知，与静态不同，在附着流动时，同一攻角下升力系数在上仰和下俯过程中是不相同的.升力系数在整个翼型振荡周期内形成一个椭圆形的气动力迟滞闭环.由于流动处于附着状态，所以动态升力系数与静态升力系数在数值上差别不大.在非定常和定常升力之间存在一个时间延迟，这一时间延迟可以由Theodorsen理论计算得到.比较ARMA 模型、CFD 模拟和Theodorsen理论计算的结果可以看出，ARMA 模型对样本工况的气动力迟滞回线与CFD 计算结果基本吻合.同时Theodorsen理论计算结果与两者的差别很小，说明CFD 计算结果与理论计算结果吻合良好.由于Theodorsen理论计算是在气体不可压缩的假设下建立的，而CFD 计算需要大量计算成本，所以采用ARMA 模型在计算成本较低的前提下获得满意的动态气动载荷预测精度就具有普适性的优势.

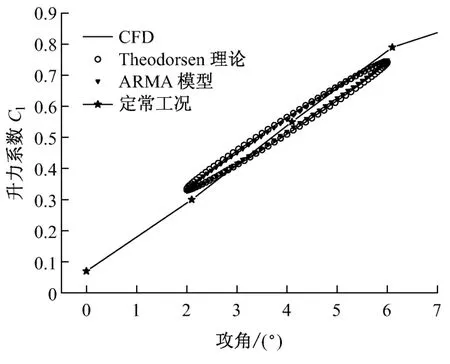
图2 不同模型的升力系数预测Fig.2 Lift coefficient predicted by different models

采用所建ARMA 模型对其他工况的非定常气动载荷进行预测，注意攻角的变化范围应小于静态失速攻角.图3给出了ARMA 模型对平均攻角α0＝4°时，振荡振幅Δα＝2°、1°和衰减频率k＝0.050、0.060的4个工况以及平均攻角α0＝2°，Δα＝2°时衰减频率k＝0.050、0.060的2个工况下升力系数的预测结果.从图3 可以看出，对比CFD 计算结果，ARMA 模型的预测结果十分精确.ARMA 模型在附着流动工况下对非定常气动载荷有很好的预测能力.

3.2 流动分离工况

当攻角在较大数值（接近或超过静态失速攻角）处变化时，由于分离的发生，非线性现象得到加强.图4给出了CFD 计算得出的升力系数在α0＝8°、k＝0.050和Δα＝5.5°时的变化曲线，同时建立Volterra级数模型和ARMA 模型样本工况进行对比分析.由于过高的记忆长度会提高模型系统辨识的难度，此处选取记忆长度M＝5.从图4 可以看出，在流动分离工况下，升力系数迟滞回线不再呈椭圆形，这与流动附着时的Theodorsen理论计算结果不同.在翼型上仰阶段，失速有被延迟的迹象，而在下俯阶段重新附着的过程也存在迟滞.同时，升力系数的迟滞回线出现交叉，说明流动的复杂程度较高.而迟滞回线的闭环明显要大于附着流动时，说明在流动分离工况下，动态气动载荷的变化范围大于附着流动工况.

图3 ARMA 模型对不同工况下升力系数的预测Fig.3 Lift coefficient predicted by ARMA model under different conditions

图4 ARMA 模型和Volterra级数模型的预测对比Fig.4 Comparison of prediction results between ARMA and Volterra series model

在流动分离工况下，ARMA 模型对CFD 计算结果的预测精度大大降低，表明此工况下ARMA模型很难捕捉到响应的实时变化.这是因为ARMA模型只适用于模拟弱非线性的问题，而升力系数在流动分离时的动态响应呈现较高的非线性特征.Volterra级数模型对较强非线性问题的模拟能力高于ARMA 模型，所以从图4可以看出，Volterra级数模型对于训练样本工况的预测与CFD 计算结果吻合更好.采用Volterra级数模型对其他工况进行预测，其结果与CFD 计算结果的对比见图5.图中所示的测试工况分别是Δα＝5.5°、10°和k＝0.026，0.050，0.060，0.077的4种组合.由图5可知，Volterra级数模型对样本工况以及其他工况除细微差别外整体预测精度很高.说明Volterra级数模型在流动分离工况下可以比较精确地预测翼型所受的非定常气动载荷.图4和图5的计算结果也表明，记忆长度M＝5已经能够保证模型的精度.

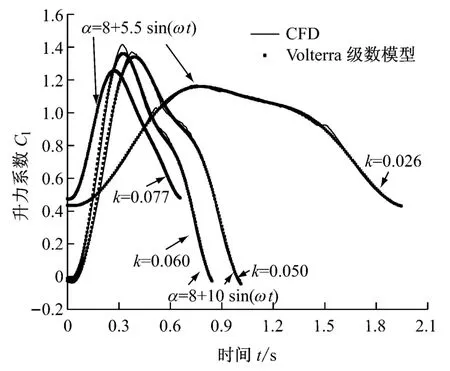
图5 Volterra级数模型对不同工况下升力系数的预测Fig.5 Lift coefficient predicted by Volterra series model under different conditions

4 结 论

（1）ARMA 模型在流动附着工况下可以很好地预测翼型非定常气动载荷的变化，但在流动分离工况下其预测能力较差.

（2）Volterra级数模型在流动分离工况下的预测能力较ARMA 模型有了很大提高.其对非定常气动载荷的预测结果与CFD 计算结果吻合较好，相比具有较高的精度.

（3）采用ARMA 模型和Volterra级数模型预测各自适应工况的非定常气动载荷是可行的.由于ARMA 模型和Volterra级数模型只需要一个工况的CFD 计算数据作为样本去辨识各自的模型待定参数，而一旦辨识好后只需几秒时间就可预测其他工况的非定常气动载荷.因此，这2种只需较小计算成本的降阶模型为非定常气动载荷的预测、相关的气动弹性分析以及风力机叶片的设计和优化提供了一种有效的方法.

［1］LEISHMAN J G，NGUYEN K Q.State-space representation of unsteady airfoil behavior［J］.AIAA Journal，1990，28（5）：836-844.

［2］HANSEN MOL.Aerodynamics of wind turbines［M］.London，UK：Earthscan，2008.

［3］刘雄，马新稳，沈世，等.风力机柔性叶片振动变形对其气动阻尼的影响分析［J］.空气动力学学报，2013，31（3）：407-412.

LIU Xiong，MA Xinwen，SHEN Shi，etal.Analysis of the influence of vibration and deformation of the blade on the aerodynamic damping［J］.Acta Aerodynamica Sinica，2013，31（3）：407-412.

［4］俞国华.水平轴风力机叶片失速问题研究［D］.上海：上海交通大学，2013.

［5］周正，李春.风力机翼型等速上仰动态失速数值模拟［J］.能源研究与信息，2013，29（4）：196-200.

ZHOU Zheng，LI Chun.Numerical simulation of identical pitching wind turbine airfoil dynamic stall［J］.Energy Research and Information，2013，29（4）：196-200.

［6］杨锡运，孙翰墨.基于时间序列模型的风电场风速预测研究［J］.动力工程学报，2011，31（3）：203-208.

YANG Xiyun，SUN Hanmo.Wind speed prediction in wind farms based on time series model［J］.Journal of Chinese Society of Power Engineering，2011，31（3）：203-208.

［7］徐敏，陈刚，陈士橹，等.基于非定常气动力低阶模型的气动弹性主动控制律设计［J］.西北工业大学学报，2005，22（6）：748-752.

XU Min，CHEN Gang，CHEN Shilu，etal.Design method of active control law based on reduced order model of unsteady aerodynamics for aeroelasticity［J］.Journal of Northwestern Polytechnical University，2005，22（6）：748-752.