基于耗散理论的超超临界机组PID非线性协调控制研究

谷俊杰，孙大龙

（华北电力大学能源动力与机械工程学院，河北保定071003）

超超临界机组协调系统是一个三输入三输出的具有强耦合性的系统.当煤水比控制品质好时，超超临界机组协调系统可以简化为双输入双输出的系统，即表现为给煤量和主蒸汽调门开度对负荷和主蒸汽压力的影响［1］.

超超临界机组协调系统由锅炉系统和汽轮机系统2部分组成，其中锅炉系统较汽轮机系统而言具有较大的延迟，同时又由于直流锅炉蓄热系数较小，因此当变负荷运行或煤种发热量变化较大时，容易造成主蒸汽压力波动，影响机组的安全性.针对超超临界机组上述动态特性，学者对其协调控制进行了许多研究.针对单元机组的多变量特性，房方等［2］采用多变量解耦的方法进行协调系统的设计；针对被控对象的多干扰特性，刘翔等［3］设计了自抗扰控制器；针对单元机组的非线性特性，韩璞等［4-5］采用Backstepping方法构造了PID 协调控制器.虽然这些理论研究存在一定的局限性和不足，但它们为优化机组协调控制品质提供了新的思路，并给出了理论支持.

动态系统的耗散概念是由Willems引入的［6］，Hill等不断发展和完善了耗散系统的概念.耗散理论给出了一种控制系统设计和分析的新思路，即从能量角度对动态系统的稳定性进行分析.目前，耗散理论得到了很好的发展，并且已经应用于机电控制和机器人控制上，取得了很好的控制效果［7］.

笔者首先将建立的超超临界机组非线性模型移至平衡点，简化该模型，并将积分项引入系统中，同时根据控制输入量和输出量的不同将模型分解为2个子系统.然后根据“如果某供给率对于特定的储能函数是严格耗散的，那么在这一供给率下，与之对应的动态系统为稳定系统”这一理论，分别对2个子系统进行控制器设计.最后将该控制器应用到1 000 MW 超超临界机组中进行仿真验证.

1 数学模型及其预处理

所采用的数学模型为de Mello等建立的燃煤机组通用简化模型，模型［8］如下：

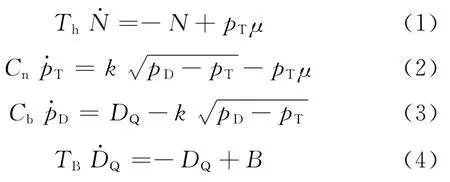
式中：Th为汽轮机与再热器时间常数；Cn为蒸汽管道蓄热系数；Cb为水冷壁蓄热系数；TB为锅炉惯性等效时间常数；N为机组的实际输出功率；pT为主蒸汽压力；pD为汽水分离器出口压力；DQ为锅炉内部汽水系统吸收的热量；μ为汽轮机调门开度；B为送入锅炉炉膛的燃料量.

系统的平衡点为

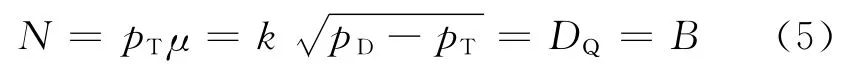
令系统的功率给定值为NZ，主蒸汽压力给定值为pTZ，将系统的工作点移至平衡点：

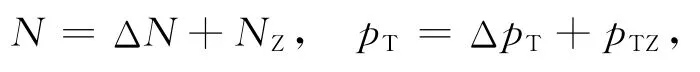
式中：ΔN为负荷给定值NZ和实际输出值之间的偏差；ΔpT为主蒸汽压力给定值pTZ和实际输出值之间的偏差；ΔμT为在负荷给定值NZ和主蒸汽压力给定值pTZ下对应的调门开度和当前状态下调门开度的偏差；ΔpD为在负荷给定值NZ和主蒸汽压力给定值pTZ下对应的汽水分离器出口压力和当前状态下汽水分离器出口压力的偏差；ΔDQ为在负荷给定值NZ和主蒸汽压力给定值pTZ下对应的锅炉吸热量和当前状态下锅炉吸热量的偏差；ΔB为在负荷给定值NZ和主蒸汽压力给定值pTZ下对应的燃料量和当前状态下燃料量的偏差.

将式（6）带入式（1）～式（4）中，模型变为

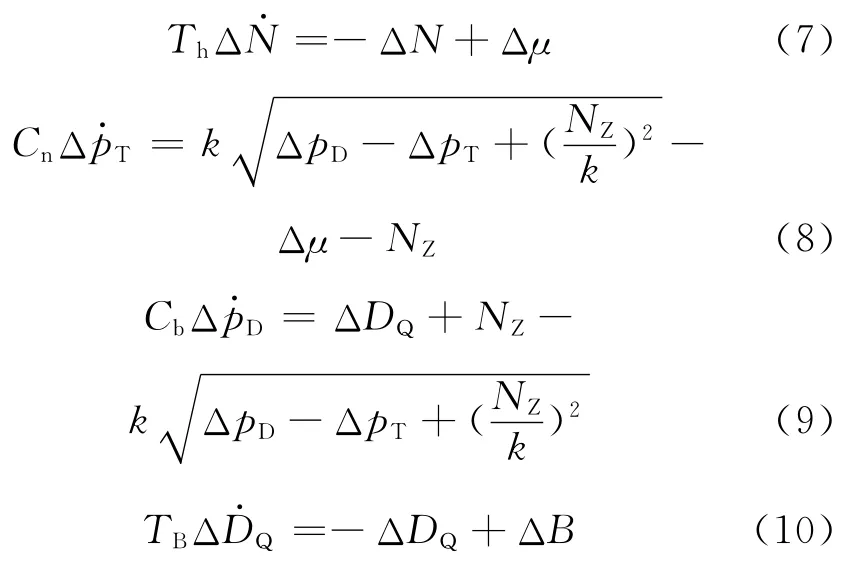
2 线性系统耗散控制律设计

令线性系统为

式中：x（t）为状态向量，x（t）∈Rn；w（t）为输入向量，w（t）∈Rm；y（t）为输出向量，y（t）∈Rp.

定义供给率为

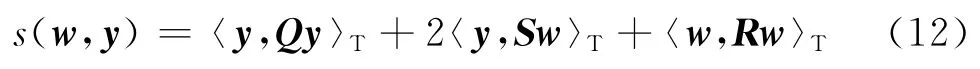
式中：Q、S和R为实数矩阵，且Q与R为对称矩阵；〈a，b〉T形式表示积分.

2.1 定理1［9］

如果Q＝QΤ≤0，且存在一个正定矩阵P满足不等式（13），那么式（11）表示的线性系统为严格耗散系统，其中.

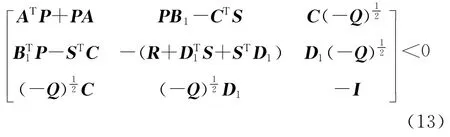
式中：I为单位矩阵.

将控制输入u＝u（t）引入到线性系统中，得到该系统的表达式为

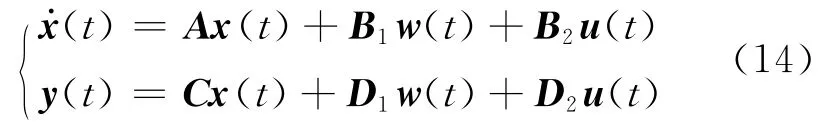
2.2 定理2［9］

一个使式（14）表示的系统为严格耗散的状态反馈控制器u＝Kx存在的充分条件为存在一个正定矩阵X和一个适当维数矩阵W，且满足不等式（15）成立，此时的状态反馈增益矩阵K＝WX-1.

3 一类非线性系统耗散控制律设计

在定理3［10］中令双输入单输出非线性系统为

式中：x和φ为状态变量，x∈Rn，φ∈R2；u为输入变量，u∈R2；ρ为干扰量，ρ∈R2；y为输出量；f（x，φ，ρ）、q（x，φ，ρ）和h（x，φ）为函数，均满足Lipschitz条件，且f（0，0，0）＝0，q（0，0，0）＝0，h（0，0）＝0.

下面介绍4个假设条件：

（1）f（x，φ，ρ）-f（x，φ，0）与φ无关.

（2）存在一个光滑函数R（x，φ），对所有（x，φ）和ρ都满足如下不等式：

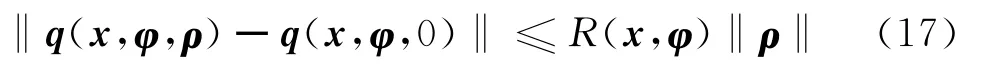
（3）存在一个正数κ、一个K∞类函数λ（·）和一个正定光滑实值函数V（x），使得对于所有x和ρ满足如下不等式：

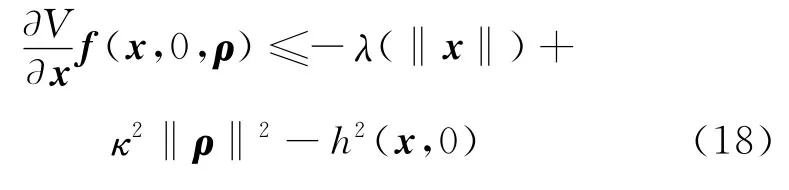
（4）输出函数h（x，φ）满足下式：

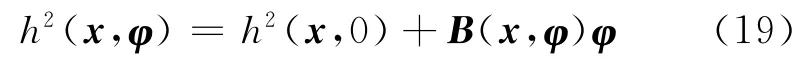
式中：B（x，φ）为光滑函数.

如果双输入单输出非线性系统满足上述4个假设条件，则对某个ζ＞0，存在K∞类函数λ（·）和正定严格光滑函数G（x，φ），并且能够找到光滑反馈控制律u＝u（x，φ），使得对其所有的（x，φ）和ρ均满足不等式（20）成立，那么在光滑反馈控制律u＝u（x，φ）的作用下，式（16）表示的双输入单输出非线性系统是全局渐进稳定的.

此时控制律为

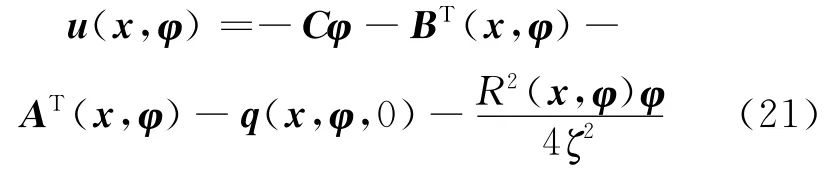
4 超超临界机组耗散控制律设计

为使系统更好地跟踪给定值，确保系统稳定后输出量与给定值之间无静态差，在系统中加入了积分项，并将原系统分为2个子系统，即子系统Ⅰ和子系统Ⅱ.

子系统Ⅰ为

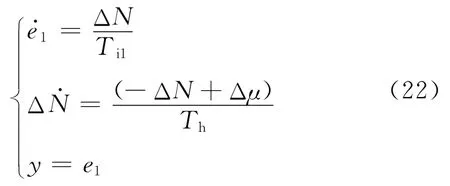
其中，Ti1为积分时间常数，Δμ为系统输入，y和e1为系统输出.

子系统Ⅱ为

其中，Ti2为积分时间常数，Δμ、e2和ΔB为系统输入，y为系统输出.

4.1 子系统Ⅰ的控制器设计

由于子系统Ⅰ为线性系统，因此采用第2节的方法进行控制器设计.当没有加入控制输入变量时，子系统Ⅰ变为

此时x＝［e1ΔN］T，，B1＝［0 0］T，C＝［1 0］，D1＝［0］.同时令Q＝-I，S＝0，R＝κ1I，P＝I.将上述矩阵带入不等式（13）中可得

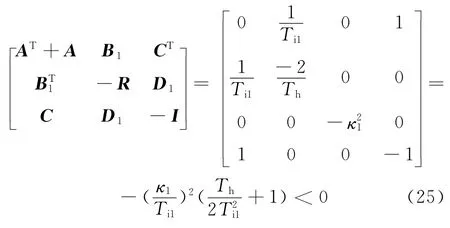
由于κ1为正数，因此式（25）恒成立，故在供给率Q＝-I，S＝0，R＝κ1I时，式（24）表示的系统为严格耗散系统.

在式（24）表示的系统中加入控制输入变量后可得

此时x＝［e1ΔN］T，，B1＝［0 0］T，B2＝T，C＝［1 0］，D1＝［0］，D2＝［0］，u（t）＝Δμ.同时Q＝-I，S＝0，R＝κ1I，P＝I.由文献［9］可知X＝P-1＝I，将上述矩阵代入不等式（15），化简后可得

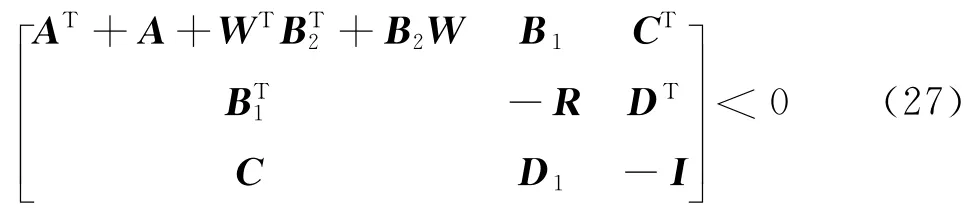
由定理2可知，只要存在适当维数的矩阵W，满足不等式（27）成立，那么式（26）表示的系统就存在状态反馈控制律，且控制律为

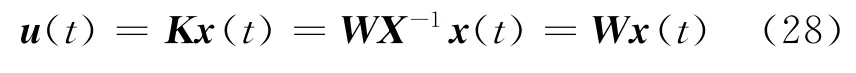
假定矩阵W＝［-b1Th＋c1-b2Th＋c2］，其中a1、a2、b1、b2、c1和c2均为非负数.将矩阵W带入不等式（27）可得

令c2＝1，κ1＞0，当满足且a2、b2不同时为0时，式（29）恒成立，式（26）表示的系统是严格耗散的，此时状态反馈控制律为

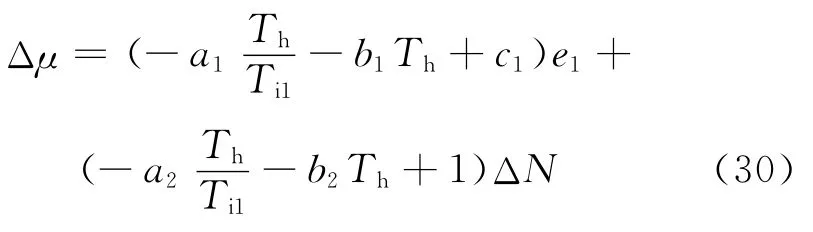
4.2 子系统Ⅱ的控制器设计

在子系统Ⅱ中加入扰动量ρ后，子系统Ⅱ变为

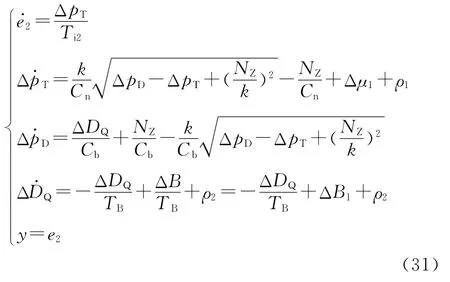
从式（31）表示的系统的状态方程可以看出，该系统为一个双输入单输出的非线性系统，其中系统输入为Δμ和ΔB，系统输出为y.因此采用第3节的方法对子系统Ⅱ进行控制律设计.

首先验证变型后的系统是否满足定理3中的各个假设条件，其中令x＝［e2ΔpD］T，y＝e2，φ＝［ΔpTΔDQ］T，u＝［Δμ1ΔB1］T，q（x，φ，ρ）＝.

下面对各个假设条件进行验证：

（1）f（x，φ，ρ）-f（x，φ，0）＝0与φ无关.

（2）当R（x，φ）＝时，对于所有的（x，φ）和ρ均满足不等式（17）成立.

（4）当h（x，0）＝0，φ＝［ΔpTΔDQ］T，，由计算可知当时，式（19）成立.

由此可知，式（31）表示的系统均满足以上假设条件.因此，一定存在光滑反馈控制律u＝u（x，φ）和一个正数ζ，使得该系统是全局渐进稳定的.

令控制律为

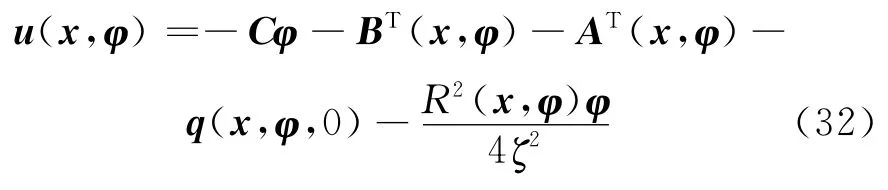
利用文献［10］中的方法可求得A（x，φ）＝，B（x，φ）＝.由于ΔpD- ΔpT很小，因此进行如下近似：×，此时q（x，φ，0）＝T，另有R（x，φ）＝.在求解过程中为了便于计算，进行如下近似：

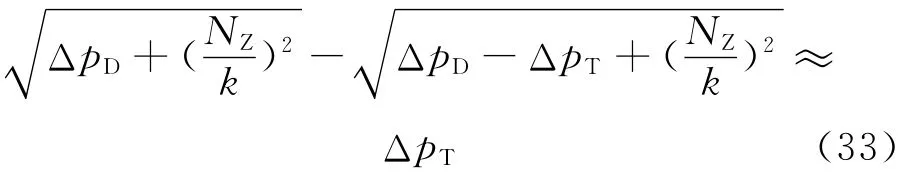
由定理3可知，在此控制律作用下，系统在平衡点处是全局渐进稳定的.

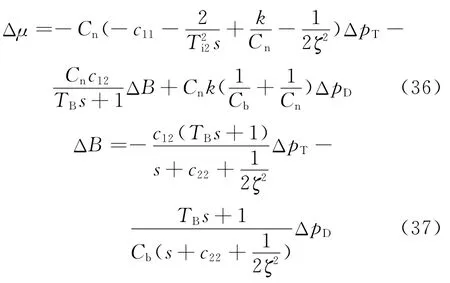
综合上述推导，得到了超超临界机组耗散控制律，将控制律转变为PID 协调控制器并给出其系统框图，如图1所示.

5 仿真研究

5.1 变工况试验

对某电厂1 000 MW 超超临界机组［11］运行工况进行仿真，该机组初始状态为满负荷运行，N＝1 000 MW，pT＝24.95 MPa，Cn＝15.473，Cb＝10.047，TB＝260s，Th＝8s，k＝2.405.从理论上讲，只要满足，a2、b2不同时为0，c11、c12、c22和ζ均为正数，系统就是稳定的.为了使仿真效果更好，仿真参数取值如下：a1＝0.000 1，b1＝0.000 875，c1＝0，a2＝0.12，b2＝0.1，c11＝0.005 7，c12＝0.000 1，c22＝9.95，ζ＝10，Ti1＝0.8s，Ti2＝28s，通过验证可知此时满足系统上述假设条件成立.

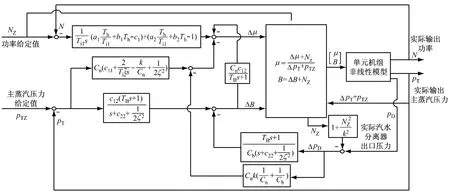
图1 超超临界机组PID协调控制系统框图Fig.1 Block diagram of the PID coordinated control system for ultra supercritical units

为了使仿真过程更接近实际情况，令负荷以10 MW／min的速率进行升降，机组采取滑压运行方式，其中滑压关键点参数为（1 000 MW，24.95 MPa）、（950 MW，24.25 MPa）和（980 MW，24.75 MPa）.试验过程为在200s处将负荷由1 000 MW降至950 MW，然后在1 500s处将负荷由950 MW升至980 MW.图2给出了1 000 MW 超超临界机组变工况试验结果.由图2可知，该机组在变工况运行时，无论是负荷还是主蒸汽压力均能够较好地跟随给定值，且两者达到稳定时的波动量均不大.

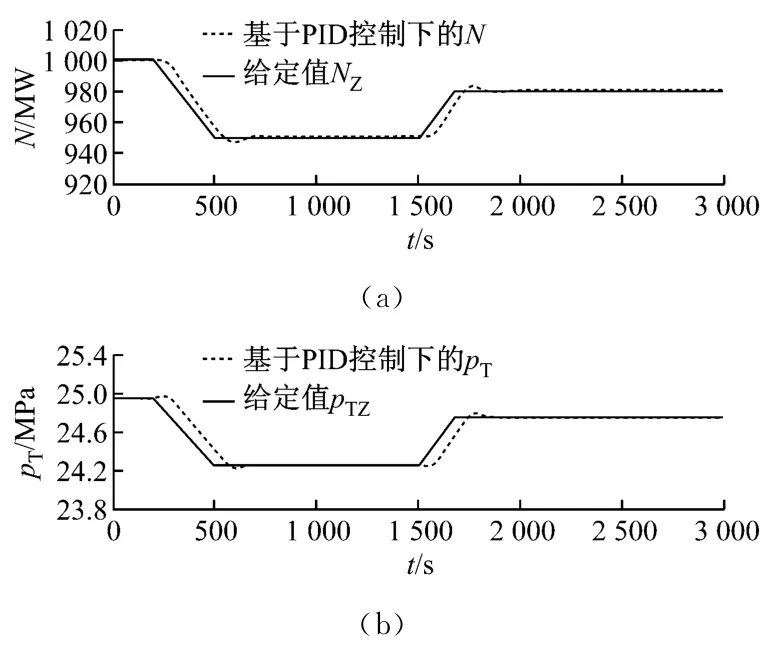
图2 1 000 MW 超超临界机组变工况试验结果Fig.2 Variable conditions test resuts of the 1 000MW ultra supercritical unit

5.2 抗干扰性能试验

机组在初始时刻以满负荷状态稳定运行，在200s处负荷侧加入5 MW 阶跃扰动信号，在1 500 s处主蒸汽压力侧加入0.1 MPa阶跃扰动信号.图3给出了1 000 MW 超超临界机组协调控制系统抗干扰性能试验结果.由图3可以看出，依据耗散理论所设计的PID 协调控制器能够有效地消除扰动的影响，使被控变量快速恢复到稳定状态，且压力与负荷相互影响较小.

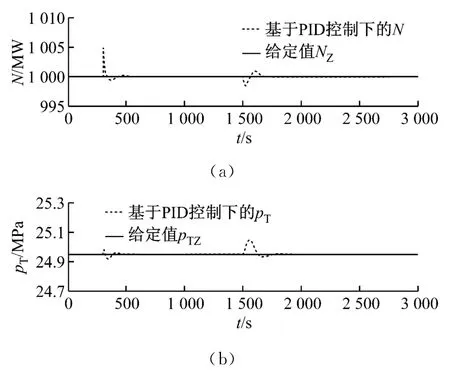
图3 1 000 MW 超超临界机组协调控制系统抗干扰性能试验结果Fig.3 Step responses of disturbance test results of the coordinated control system for the 1 000 MW ultra supercritical unit

6 结 论

依据耗散理论，对线性系统和非线性系统进行了耗散性分析并构造了状态反馈控制律，然后将其应用到1 000 MW 超超临界机组模型中，得到了该机组PID 协调控制器.仿真结果表明，该控制器能够对机组进行很好的协调控制，并且表现出良好的给定值跟随性和抗干扰性.

［1］谷俊杰，曹晓威，王丕洲，等.超临界直流锅炉煤水比控制系统机理建模及定量反馈控制［J］.动力工程学报，2013，33（12）：947-954.

GU Junjie，CAO Xiaowei，WANG Pizhou，etal.Mechanism modeling and quantitative feedback control for fuel-water ratio control system of supercriticalonce-through boilers［J］.Journal of Chinese Society of Power Engineering，2013，33（12）：947-954.

［2］房方，刘吉臻，谭文.火电单元机组协调控制系统的多变量IMC-PID 设计［J］.动力工程，2004，24（3）：360-365.

FANG Fang，LIU Jizhen，TAN Wen.Multivariable IMC-PID design in the coordinated control system for fossil unit power plants［J］.Power Engineering，2004，24（3）：360-365.

［3］刘翔，姜学智，李东海，等.火电单元机组机炉协调自抗扰控制［J］.控制理论与应用，2001，18（增刊）：149-152.

LIU Xiang，JIANG Xuezhi，LI Donghai，etal.Coordinated autodisturbance-rejection control for boilerturbine unit［J］.Control Theory ＆ Applications，2001，18（Sup）：149-152.

［4］韩璞，魏乐.锅炉-汽轮机单元协调控制的反推PID 方法［J］.中国电机工程学报，2010，30（2）：17-22.

HAN Pu，WEI Le.Backstepping PID methods for coordinated control of boiler-turbine units［J］.Proceedings of the CSEE，2010，30（2）：17-22.

［5］王印松，田瑞丽，白洁，等.基于backstepping方法的单元机组协调系统非线性控制［J］.华北电力大学学报，2006，33（5）：45-55.

WANG Yinsong，TIAN Ruili，BAI Jie，etal.Nonlinear control for boiler-turbine coordinate systems of power unit based on backstepping［J］.Journal of North China Electric Power University，2006，33（5）：45-55.

［6］兰海.基于耗散理论的电力系统鲁棒非线性控制研究［D］.哈尔滨：哈尔滨工程大学，2004.

［7］LOZANO R，BROGLIATO B Z，EGELAND O，et al.Dissipative systems analysis and control［M］.London，United Kingdom：Kluwer Academic Publisher，2000.

［8］田瑞丽.基于反步法的汽轮机发电机组协调控制系统研究［D］.保定：华北电力大学，2006.

［9］于显利.车辆主动悬架集成控制策略研究［D］.长春：吉林大学，2010.

［10］兰海，李殿璞，原新，等.一类MIMO 非线性系统的L2增益干扰抑制方法［J］.哈尔滨工程大学学报，2004，25（6）：751-755.

LAN Hai，LI Dianpu，YUAN Xin，etal.L2gain disturbance attenuation for a class of MIMO nonlinear systems［J］.Journal of Harbin Engineering University，2004，25（6）：751-755.

［11］谷俊杰，谭俊龙，孙玉洁，等.超临界锅炉蓄热系数计算［J］.锅炉技术，2012，43（3）：1-4.

GU Junjie，TAN Junlong，SUN Yujie，etal.The calculation of supercritical boiler heat storage coefficient［J］.Boiler Technology，2012，43（3）：1-4.