单级轴流风扇单音噪声源及噪声辐射特性的数值研究

张建华，楚武利，2，刘 炜

（1.西北工业大学动力与能源学院，西安710072；2.先进航空发动机协同创新中心，北京100191；3.华中科技大学机械科学与工程学院，武汉430074）

由于环境保护的需要，风机噪声指标越来越引起人们的重视.近10年来旋转机械噪声成了一个热门研究课题.目前，对轴流风机噪声产生机理和预测方法的研究主要有3个方面：单转子宽频噪声、级转静干涉单音噪声和叶尖涡噪声.Wright等［1-3］研究了轴流叶轮机械转子气动力与噪声的关系，得到了单转子轴流风机的噪声产生机理：转子叶片是主要的噪声源，噪声以宽频为主，端壁边界层和转子叶尖的干涉形成的湍流尾迹脱落是噪声产生的主要原因，气动力作用于叶尖泄漏流推动了转子尾迹流动和通道内的二次流流动.然而对于亚音速（Ma＜0.3）单级风扇而言，级转静干涉噪声是此类叶轮机械主要的离散单音噪声分量，静叶表面的非定常压力脉动是此类噪声的主要噪声源，其来源于转子尾迹对下游静叶的周期性冲击［4-5］.这种非定常压力脉动通常可以通过高效和高精度的商用CFD 软件获得.目前，对于轴流风扇［6-9］及轴流泵［10］噪声的预测多采用混合气动声学方法（HCAA），该方法的本质是将复杂的噪声计算分成2个独立的过程，首先基于三维黏性非定常流场（URANS），采用商用CFD软件计算获得噪声源，再采用Lighthill声类比理论的FW-H 方程耦合URANS声源信息获得远场噪声辐射，但这种方法并没有考虑实际存在的外壳体对声波的作用，误差较大.为了获得更准确的预测结果，Lee 等［11-12］在预测中引入kirchhoff-helmholtz BEM 技术，这种技术在计算中考虑了声源外部固体边界对声传播的散射和反射作用.Cai等［13］和Hu等［14］采用多区域边界元方法（MDBEM）分别预测了工业用离心风机和单级轴流风机噪声辐射，取得了较好的效果.然而上述声学边界元方法的本质是利用自由空间的格林函数积分离散Lighthill方程，目前的格林函数积分解法只能针对空间简单几何边界求解，而对于空间复杂几何边界难以得到准确解，对于这类复杂边界问题只能将其在自由空间内简化求解，因此忽略了声波在复杂固壁上的反射和散射等作用.为了克服这个缺陷，Koopmann 等［15］基于Lighthill方程的变分形式，采用有限元方法求解，这种方法可以将传播中的声源在声场空间离散以考虑结构和声的相互作用，适用于任何复杂的几何结构.

对于离散单音噪声而言，壁面非定常流场的压力脉动是最为直接的噪声源，为了快速获取风扇的噪声特性，Liu等［16］根据Lighthill声类比理论中声源信息和噪声的关系，通过分析声源区频谱定性地预测了工业用离心风机的噪声辐射特性.Tan等［17］应用此方法定性分析了离心压缩机噪声源的强度和位置.

笔者以单级轴流风扇为研究对象，采用数值模拟方法研究了该轴流风扇的非定常气动力和气动噪声特性，主要分为3个部分：（1）噪声源流场特性的分析；（2）基于噪声源表面压力脉动频谱分析定性确定噪声的强度和位置；（3）采用基于Lighthill声类比理论的FW-H 方程耦合URANS方法计算风扇远场噪声辐射.为了考虑复杂壁面对声波的散射和反射影响，声场计算采用声学有限元方法，即将FW-H 方程转变为频域Helmholtz弱积分形式并采用Galerkin方法离散.

1 风扇计算模型

1.1 风扇模型参数

以某单级轴流风扇为研究对象，具体参数见表1.

表1 风扇转子和静子参数Tab.1 Rotor／Stator parameters of the fan

1.2 流场计算网格及边界条件

1.2.1 网格特点

基于三维设计软件UG 建立风扇各结构的实体模型，并在Blade-Gen中分别生成风扇的转子和静子叶片通道，在Ansys Turbo-Grid中划分通道的高质量六面体结构化网格，网格拓扑采用正交性较好的H-J-C-L型网格，叶片表面周围采用O 型网格拓扑，近壁面网格节点加密处理，通道进口到叶片前缘采用J型网格拓扑，其余部分采用H 型网格拓扑，这样既可以使网格正交性达到最佳又可以避免全部采用J型网格拓扑时前缘和尾缘网格长宽比过大.转子叶顶间隙为2.5mm，采用H 型网格.转子通道最小网格面角大于25°，网格长宽比小于100，由于风扇为轴对称结构，为了节省计算资源，只计算一个级通道（转子／静子）.级通道计算域分为3部分：进口流域及转子通道计算域、静子通道及扩压段计算域和出口延伸段计算域.进口流域及转子通道网格数为349 208，静子通道及扩压段网格数为290 904，出口延伸段网格数为68 080.图1给出了转子、静子和轮毂的表面网格分布.为验证网格无关性，将各计算域网格分别加密一倍，图2为不同数量网格下风机的效率和全压升对比图.由图2可知，网格增大为原来的2倍后全压升和效率变化不大，说明此套网格已达到网格无关性要求，现用网格数量已满足计算精度需要.

图1 叶片及轮毂表面网格Fig.1 Surface mesh of the blade and hub

图2 网格无关性验证Fig.2 Grid independence validation

1.2.2 流场计算模型

采用商业CFD 软件Ansys CFX 求解此单级风扇的流场，基于有限元体积法离散Navier-Stokes方程和RNGk-ε湍流方程［18］.RNGk-ε湍流方程能准确预测旋转和曲率对流动的影响，满足所研究轴流风扇流场计算需要.空间离散采用高精度的高阶格式差分，非定常计算的时间推进格式为双时间步长全隐式格式，时间项使用二阶后向欧拉差分离散，使用压力耦合求解算法来求解连续性方程和动量方程.由于样机叶片叶尖马赫数为0.18（＜0.3），认为气流不可压缩，流动被认为是绝热的且不需要考虑进出口温差，所以计算中舍弃了能量方程.

1.2.3 边界条件

计算域介质为20 ℃、101 325Pa的空气.边界条件为：给定进口质量流量，出口静压边界条件，出口压力值为大气压101 325Pa；所有壁面采用无滑移边界条件，对近壁面流动区域采用可伸缩壁面函数法处理，基于RNGk-ε湍流模型，近壁面边界层网格节点数约为10，用以保证Y＋在30～300之间.数值计算中引入了多重参考坐标系（MRF），叶轮流域设定为转动域，其他流域设定为静止域.交界面处理：定常计算转子和静子交界面采用混合面法［11］，交界面上游（转子）流动参数周向平均后传递给下游（静子）交界面，相邻的2个通道之间采用节点一一对应的周期性交界面.非定常计算采用滑移网格技术的转／静交界面法处理，由于计算模型动、静叶片数量分别为15和16，为了节约计算资源采用了单通道处理，且通道比近似接近1∶1，采用此方法会使计算出的动静干涉非定常脉动力略高于实际结果.叶轮转动一周分成600个时间步，因此一个栅距通道内设定40个时间步，每个时间步长为3.424 6×10-5s，这个时间步长满足动态压力信号的采集需求.连续性方程、3个方向速度方程、湍动能方程和湍流耗散率方程的标准化均方根残差均设置为10-5，且计算域进出口质量流量差值小于0.5%，作为流场计算的收敛标准.非定常计算以定常计算结果为初场，每个时间步下所有求解方程残差降到10-5以下，叶轮转动3 000 个时间步，即转动5 周后，设定的监测点达到稳定的周期性波动，此时判定计算收敛.

1.3 噪声计算模型及网格

基于URANS／FW-H 方程的混合计算声学方法求解低速轴流风扇的远场噪声辐射.对于低马赫数的单级风扇，级转静干涉单音噪声是主要的单音噪声［19］.因此，声源信息中与内部湍流流动相关联的四极子声源项和与叶片厚度相关的单级子声源项被忽略，只保留由于周期性非稳定压力脉动引起的偶极子声源项.相对于时域信息而言，更关注频域信息，FW-H 方程经过Fourier变换后得到频域形式的Helmholtz波动方程，并采用声学有限元方法离散该Helmholtz波动方程，声学网格建模过程中考虑了叶片和机匣壁面对声波的散射和反射作用，具体网格划分见图3.声学网格采用非结构化的四面体网格，最大网格尺寸为18 mm，总的网格数为1 600 094，为保证在最大频率下的空间求解精度，有限元网格单元长度L必须满足：L≤c／（6fmax），c为声速，fmax为最高计算频率（3倍频＝2 190Hz）.

图3 轴流风扇声学有限元网格Fig.3 Acoustic finite element mesh of the axial flow fan

2 结果分析与讨论

2.1 转静干涉流场

任何叶轮机械的非定常流动行为是以非定常流动特征的出现为依据的，这种非定常流动特征来源于叶片表面的相对运动，而在叶片表面出现的边界层产生的尾迹结构与主流掺混，并会随着主流的传播产生新的非定常流动现象.这些非定常流动特征会在流动中进行能量交换，此外，周期性非定常流动对下游叶片的干涉是此类叶轮机械最主要的单音噪声源.因此，精准地描述非定常流动行为对于提高叶轮机械性能和降噪非常重要.

图4给出了转子出口50%叶展截面上各节点的速度随周向位置的变化，图中T表示转子转过一个通道所需的时间.转子尾迹向下游传播过程中有非常明显的尾迹亏损，在此截面的轴向速度云图（图5）中发现一个狭长的贯穿整个通道的尾迹区，此尾迹与叶顶的间隙泄漏涡掺混，加剧了叶顶区域的流动损失.同时，这种尾迹结构会与主流掺混进入下游的静叶通道，打断静叶前缘的一致性流动.

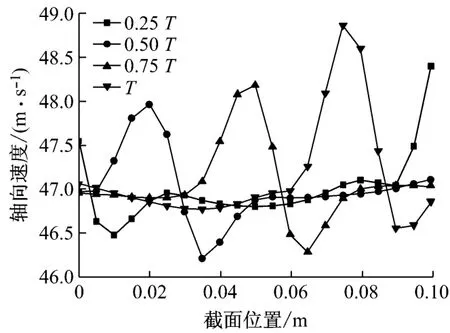
图4 转子出口50%叶展截面轴向速度随周向位置的变化Fig.4 Circumferential distribution of axial velocity on 50% span section at rotor outlet

图5 0.5T 时刻转子出口截面轴向速度分布Fig.5 Axial velocity distribution on section of rotor outlet at 0.5T

图6给出了叶片通道内50%叶展截面的熵增云图.从图6可以明显地观察到转子出口的尾迹对静叶前缘的周期性冲击作用，这种周期性冲击导致的静叶前缘的非定常压力波动正是此类叶轮机械最主要的单音噪声来源.

图7给出了静叶通道50%叶展截面上熵增和轴向涡量矢量图.图7清晰显示了转子尾迹在静叶通道中的演变过程：转子尾迹周期性扫过静叶，在静叶前缘被静叶切割，并在静叶通道内拉伸变形以及与主流掺混等.在尾迹内部由于强烈的剪切作用产生严重的气动损失，图中尾迹区的高熵分布充分说明了这一点.从图7还可以看出，尾迹在静叶通道传播过程中逐渐变宽，这是因为尾迹与静叶通道中的主流掺混降低了尾迹区的速度亏损，增加了尾迹宽度；尾迹向下游输送过程中通道内逆压梯度增大，增加了尾迹宽度.

从图7（a）可以看出，由于负射流作用［19］，在转子尾迹前后诱导出一对旋转方向相反的漩涡结构.这些漩涡与尾迹区边界层相互作用，改变了静叶表面边界层流动的发展，造成静叶表面产生更剧烈的压力波动.此外，由于周向逆压梯度作用，尾迹在向下游输送过程中使得漩涡向静叶吸力面一侧聚集，并在转子尾迹扫过静叶前，首先与静叶前缘接触而被静叶切割，并与静叶表面边界层相互作用，这些漩涡使得边界层内速度加快，加速了边界层内流动的动量和能量交换，使得通道内的尾迹亏损降低，尾迹宽度增加.

为了比较动、静叶表面压力的大小，获得准确的噪声源强度和位置，图8给出了动、静叶表面均方根压力分布.图中均方根压力的定义如下：

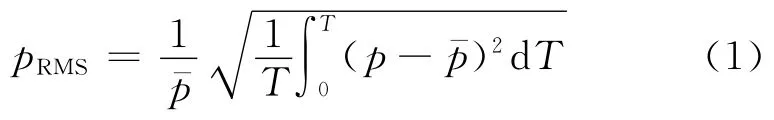
式中：为时均压力；p为瞬时压力；T为计算周期.

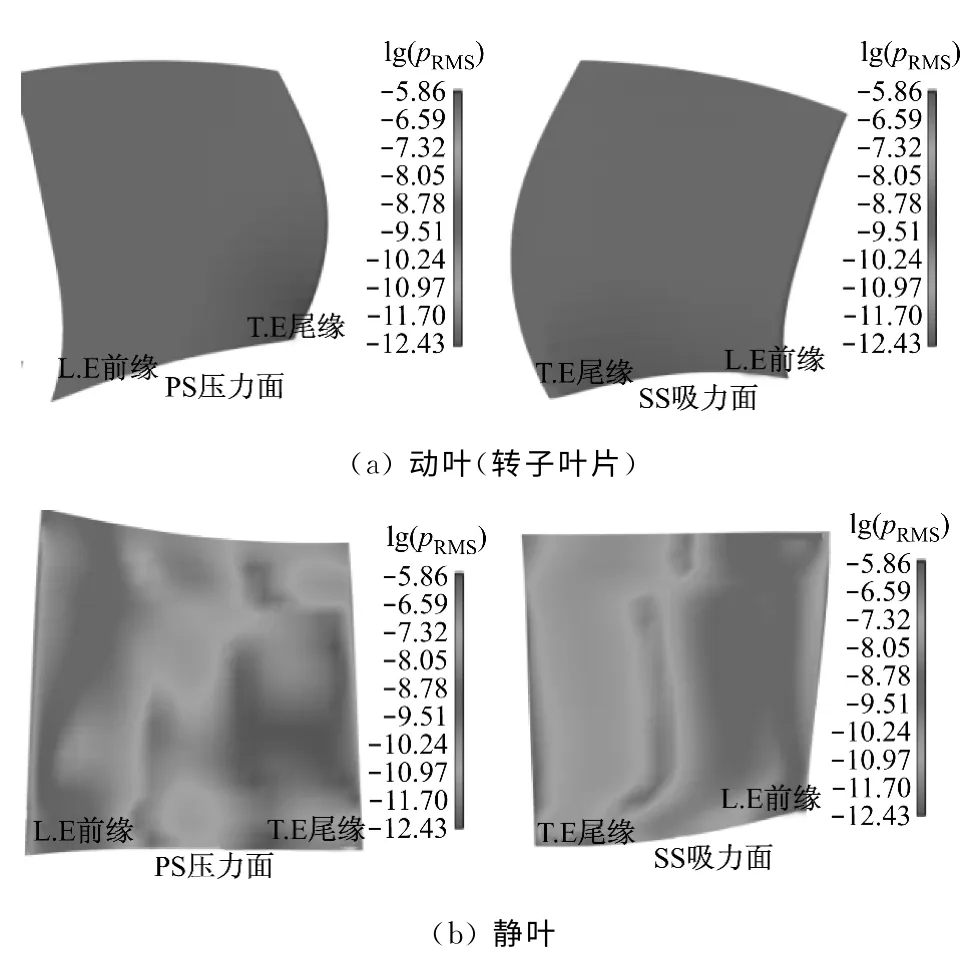
图8 动、静叶表面均方根压力分布Fig.8 RMS pressure distribution on rotor and stator surface

为了表达清晰，图8中给出了均方根压力的对数表示形式.从图8可以看出，静叶前缘吸力面一侧是压力脉动扰动最大的区域，这里受到上游转子尾迹和尾迹诱导漩涡的强烈冲击作用，而此处也是最主要的噪声源区域.同时，在静叶吸力面还发现大范围的压力波动区域，这是因为转子尾迹诱导出的漩涡由于周向逆压梯度的作用向吸力面移动，此漩涡与静叶吸力面表面的边界层相互作用，破坏了边界层内流动的一致性，增强了边界层内的流动，从而导致吸力面边界层较大范围的波动.

2.2 偶极子源辨析

图9 给出了静叶在基频（BPF）及其二倍频（2BPF）下压力波动的均方根值，左侧为静叶压力面载荷分布，右侧为吸力面载荷分布.从图9 可以看出，最大载荷分布在静叶前缘靠近吸力面区域，这是因为此处受上游转子尾迹以及尾迹诱导漩涡的周期性强烈干涉作用，使得此区域静叶表面的边界层流动剧烈.此外，从图9还可以看出，基频的幅值远高于二倍频.综上所述，基频下静叶前缘靠近吸力面区域是最主要的噪声源区域.

图9 静叶非定常载荷分布Fig.9 Distribution of unsteady aerodynamic load on stator

2.3 噪声预测结果

以叶片表面的气动载荷作为声源信息，并经过频域的FFT 变换后加载给Ffowcs Williams-Hawking方程的频域形式（即频域声学Helmholtz波动方程），来求解风扇的远场噪声辐射.计算远场噪声时，依据标准ISO 3744—1994《声学声压法测定噪声源声功率级和声音能量级 反射面上方近似自由场的工程法》建立包围声源区的场点网格.依据声学测量要求在场点网格不同位置建立9个测点，各测点距离样机对应实体表面1m，附近1m 内无发射面，依据式（3）得到测量表面平均声压级：

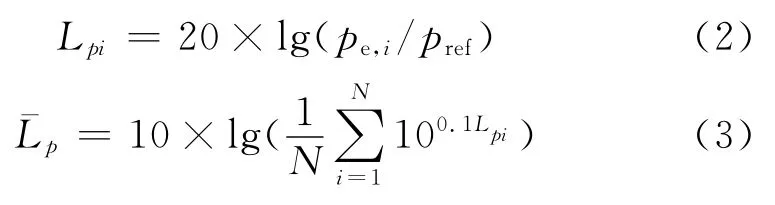
式中：N为测点数；Lpi为第i个测点的声压级；pe，i表示第i个测点的有效声压；基准声压取pref＝20×10-6Pa.

分别计算动、静叶表面偶极子激发的外场噪声辐射，图10分别给出了动、静叶表面偶极子源噪声辐射的平均声压级在不同频率（BPF、2BPF 和3BPF）下的计算结果.由图10可知，静叶表面偶极子源激发的噪声（95dB）远大于动叶（77.5dB），且以基频噪声为主，这说明由静叶表面非定常力激发的转静干涉噪声是此类叶轮机械的主要单音噪声.

图11给出了基频及其谐波轴截面声压级云图，图中上方为管道出口位置，下方为管道进口位置.从图11可以看出，噪声在管道壁面上以交替周向模态向管道进出口两侧传播，且以管道出口为主.此外基频的辐射声压级最大，最大声压级达到120dB，随着频率值衰减到2BPF，声压级幅值急剧减小，最大值减小到105dB，噪声的管道周向传播模态也有较大程度的衰减.当频率值衰减到3BPF时，其声压级值相对于基频声压几乎可忽略不计，其管道周向传播模态进一步衰减，但是变得更加密集且没有发现明显的声场指向性.

图10 基频及其谐波的噪声模态Fig.10 SPL acoustic mode at BPF and its harmonics

图11 基频及其谐波轴截面声压级云图Fig.11 Sound pressure profile on axial section at BPF and its harmonics

以叶轮轴心位置为圆点，半径1.5m 的轴截面上间隔10°均匀布置36个监测点，监测点以管道出口位置为起始零点.图12给出了监测点的声压级分布.从图12可以看出，声压级在轴截面上呈对称分布，管道出口处的声压级辐射高，声压级随着频率的衰减而降低，即基频下声压级最高，这与前面的声压级云图分析一致.

3 结 论

（1）上游的转子尾迹及叶顶间隙泄漏涡对下游静叶前缘的周期性干涉破坏了静叶前缘的一致性流动.这种周期性非定常干涉改变了静叶表面前缘的压力波动.尾迹与叶顶的间隙泄漏涡掺混加剧了叶顶的流动损失，使静叶前缘叶顶区域产生较大的压力波动.

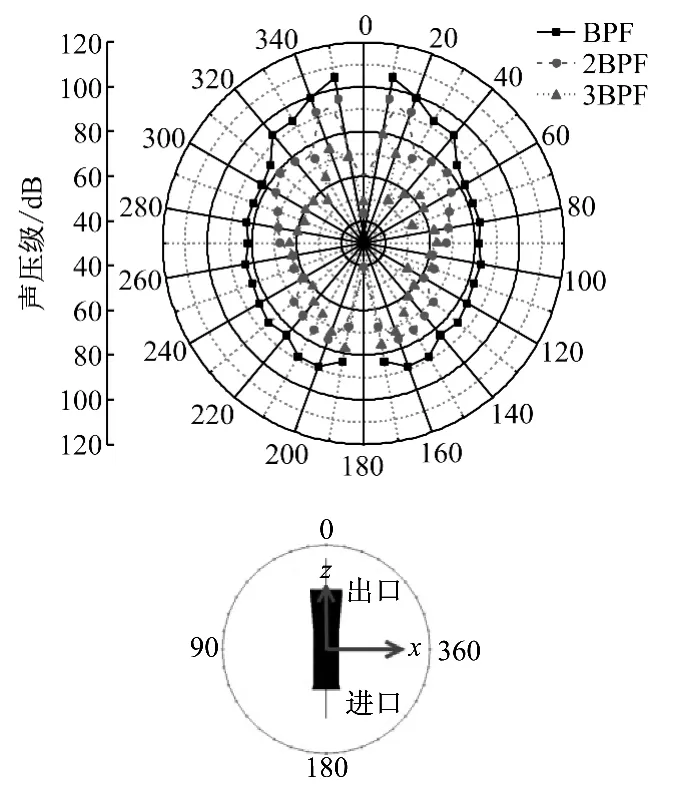
图12 声场指向性分布Fig.12 Directivity distribution of far-field SPLs

（2）由于负射流效应，在转子尾迹前后诱导出一对旋转方向相反的漩涡，这种漩涡结构在和尾迹一起向下游输送过程中首先与静叶前缘接触，并由于静叶压差作用向静叶吸力面聚集，漩涡与静叶吸力面表面边界层相互作用，加速了边界层内的动量和能量交换，造成了静叶吸力面表面更大的压力波动.

（3）噪声源的频谱分析表明，在基频下，静叶前缘靠近吸力面区域是最主要的噪声源区域.

（4）平均声压级对比分析表明，静叶表面非定常力（偶极子源）激发的转静干涉噪声是此类叶轮机械的主要单音噪声.噪声主要以基频为主，声压级随着频率的衰减而降低.此类转静干涉噪声主要从风扇管道出口向外辐射传播.

［1］WRIGHT S E.The acoustic spectrum of axial flow machines［J］.Journal of Sound and Vibration，1976，45（2）：165-223.

［2］CUMPSTY N A.A critical review of turbomachinery noise［J］.Journal of Fluids Engineering，1977，99（2）：278-293.

［3］BLAKE W K.Mechanics of flow-induced sound and vibration［M］.Orlando，Fla，USA：Academic Press，1986.

［4］FLEETER S.Discrete frequency noise reduction modeling for application to fanjet engines［J］.The Journal of the Acoustical Society of America，1980，68（3）：957-965.

［5］WOODWARD R P，ELLIOTT D M，HUGHES CE，etal.Benefits of swept and leaned stators for fan noise reduction［J］.Journal of Aircraft，2001，38（6）：1130-1138.

［6］YOUNSI M，BAKIR F，KOUIDRI S，etal.Numerical and experimental study of unsteady flow in a centrifugal fan［J］.Proceeding of the Institution of Mechanical Engineers，Part A：Journal of Power and Energy，2007，221（7）：1025-1036.

［7］KHELLADI S，KOUIDRI S，BAKIR F，etal.Predicting tonal noise from a high rotational speed centrifugal fan［J］.Journal of Sound and Vibration，2008，313（1／2）：113-133.

［8］DÍAZ A K M，FERNÁNDEZ O J M，MARIGOTA E B，etal.Numerical prediction of tonal noise generation in an inlet vaned low-speed axial fan using a hybrid aeroacoustic approach［J］.Proc IMechE，Part C：J Mechanical Engineering Science，2009，223（9）：2081-2098.

［9］万剑锋，杨爱玲，戴韧.风机叶片表面分离涡与宽频噪声辐射特性的分析［J］.动力工程学报，2014，34（9）：736-741.

WAN Jianfeng，YANG Ailing，DAI Ren.Analysis of separation vortex and broadband noise radiation of fan blade surfaces［J］.Journal of Chinese Society of Power Engineering，2014，34（9）：736-741.

［10］王风华，杨爱玲，戴韧，等.前弯叶片对轴流泵噪声辐射性能的影响［J］.动力工程学报，2011，31（6）：440-444.

WANG Fenghua，YANG Ailing，DAI Ren，etal.Effect of blade＇s forward-skewed angles on flow sound radiation of axial pumps［J］.Journal of Chinese Society of Power Engineering，2011，31（6）：440-444.

［11］LEE D J，JEON W H，CHUNG K H.Development and application of fan noise prediction method to axial and centrifugal fan［C］／／Proceeding of ASME FEDSM＇02 Fluids Engineering Division Summer Meeting，Montreal.Quebec，Canada：ASME，2002：987-992.

［12］POLACSEK C，DESBOIS-LAVERGNE F.Fan interaction noise reduction using a wake generator：experiments and computational aeroacoustics［J］.Journal of Sound and Vibration，2003，265（4）：725-743.

［13］CAI Jiancheng，QI Datong，LU Fuan，etal.Study of the tonal noise of a centrifugal fan at the blade passing frequency.PartⅠ：aeroacoustics［J］.Journal of Low Frequency Noise，Vibration and Active Control，2010，29（4）：253-266.

［14］HU Binbin，OUYANG Hua，WU Yadong，etal.Numerical prediction of the interaction noise radiated from an axial fan［J］.Applied Acoustic，2013，74（4）：544-552.

［15］KOOPMANN G H，NEISE W，CUNEFARE K A.Fan casing noise radiation［J］.Journal of Vibration and Acoustics，1991，113（1）：37-42.

［16］LIU Q，QI D，MAO Y.Numerical simulation of centrifugal fan noise［J］.Proceedings of Institute Mechanical Engineers，Part C：Journal of Mechanical Engineering Science，2006，220（8）：1167-1178.

［17］TAN Hongtao，QI Datong，LIU Fuan.Identification of acoustic dipole source in a propylene centrifugal compressor stage ［C］／／Proceeding of ASME Turbo Expo 2010：Power for Land，Sea and Air.Glasgow，UK：ASME，2010：14-18.

［18］YAKHOT V，ORSZAG S A，THANGAM S，etal.Development of turbulence models for shear flows by a double expansion technique［J］.Physics of Fluids A，1992，4（7）：1510-1520.

［19］WECKMULLER C，GUERIN S，ASHCROFT G.CFD-CAA coupling applied to DLR UHBR-fan：comparison to experimental data［C］／／15thAIAA／CEAS Aeroacoustics Conference （30th AIAA Aeroacoustics Conference）.Miami，Florida：AIAA，2009：1-11.