正态性检验的几种方法比较

杨 斌

0 引言

正态分布是许多检验的基础，在实际使用统计分析时,人们总是乐于正态假定,但该假定是否成立,牵涉到正态性检验。比如χ2检验、F检验以及t检验等在总体不是正态分布时是没有任何意义的，因此，对一个总体是否来自正态总体的检验至关重要。另外，方差分析、回归分析等统计分析中也都首先验证待分析的数据是否服从正态分布，检验样本的正态性一直以来都是统计学里比较重要的问题，检验方法的多样性使得这个问题始终保持着活力。历史上不仅有D'Agostino,Kolmogorov-Smirnov(Lillie检验),Shapiro-Wilk,Ryan-Joiner等一系列的检验方法,还有Anderson-Darling test(ad检验),Cramer-von Mises test(cvm检验),Pearson chi-square test(pearson检验),Shapiro-Francia test(sf检验)等这些都是检验样本正态性的方法[1]。但对这几种不同的检验方法，有些检验法针对小样本,有些针对大样本,有些则对于任何大小的样本量都可以用,但可能效果不太好,这些不同的检验方法随着样本的变化有何不同？检验的错误率大小如何？检验的结果是否合理，这些问题都需要进一步分析和解决。本文概述了Anderson-Darling test(ad检验)、Pearson chi-square test(pearson检验)以及Kolmogorov-Smirnov(Lillie检验)的统计原理，通过随机模拟实现了这几种不同检验方法的结果，并针对ad检验给出了具体检验的统计方法，着重比较了ad检验、cvm检验、lillie检验、pearson检验、sf检验这五种方法的优劣。分析了来自不同总体的样本数据，并做了结论分析，为更好的做正态性检验提供了更加准确的方法参考。

1 检验的统计原理

1.1 ad检验原理

已知样本为 X1，X2，…，Xn，做如下检验：

H0:Xi～N(0，1)↔H1:Xi不服从N(0，1)(i=1，2，…，n)

zi=，其中Φ(x)表示标准正态分布函数 ：，mean(x)表示样本的均值：，sd(x)表示样本标准差：

可以知道[2],这里 Fn是经验分布函数，F0是零假设下样本服从的分布（在本文中F0为标准正态分布）。在文献[3]中提到了A2的特征函数为：，由逆转公式及傅里叶变换：

1.2 lillie检验原理

该检验是对Kolmogorov-Smirnov检验的修正，故先介绍Kolmogorov-Smirnov检验，Kolmogorov-Smirnov检验是基于经验分布函数（ECDF）的检验。其检验方法是以样本数据的累积频数分布与理论正态分布比较，若两者间的差距很小，则推断该样本取自某正态分布族。F0(x)表示分布的分布函数，Fn(x)表示一组随机样本的累计概率函数。，设 D 为 F0(x)与Fn(x)差距的最大值，定义如下式:D=max|Fn(x)-F0(x)|，当原假设为真时，D的值应较小，若过大，则怀疑原假设，从而，对于给定的 α ，拒绝域为：R={D ＞d }，p=P{D ＞d}=α,结论：当实际观测 D＞Dn，则接受 H1，反之则不拒绝 H0假设。又，该检验是对Kolmogorov-Smirnov检验的修正，参数未知时，由可计算得检验统计量的值。

1.3 pearson检验原理（基于经验分布函数（ECDF）的检验）

检验统计量为[4]：

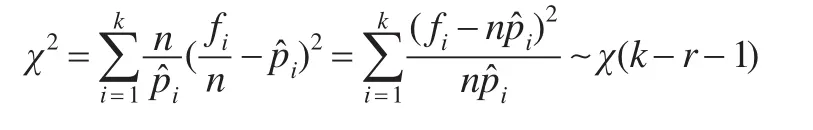
其中r是被估参数的个数，fi为样本中Ai发生的实际频数,npi为H0为真时Ai发生的理论频数。若 χ2=0，则 fi=npi,意味着对于Ai，观测频数与期望频数完全一致，即完全拟合。

观察频数与期望频数越接近，则χ2值越小。当原假设为真时，有大数定理，与 pi不应有较大差异，即 χ2值应较小。若 χ2值过大，则怀疑原假设。拒绝域为R={χ2≥d }，判断统计量是否落入拒绝域，得出结论。从而拒绝域为 R={χ2≥d}，对于给定的α，P{χ2≥d}=α，又，判断统计量是否落入拒绝域，得出结论。

2 检验方法

2.1 当样本来自正态总体

本文进行随机模拟的办法抽取样本 X1，X2，…，Xn～N(0，1)，而样本量n我们分别取10,100,1000，来观察检验方法的p值大小（实验次数为1000次），尝试对样本进行程序包nortest里的ad检验、cvm检验、lillie检验、pearson检验、sf检验五种检验方法分别计算得到的p值的箱线图如下:

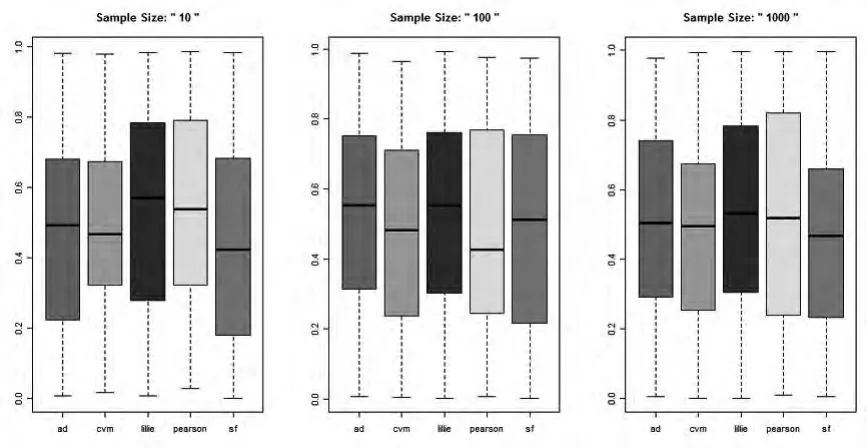
图1 样本n=10，100，1000时的箱线图

并且我们得到了判断错误率(得到p值小于0.05的次数占1000次试验的比例)如表1所示:

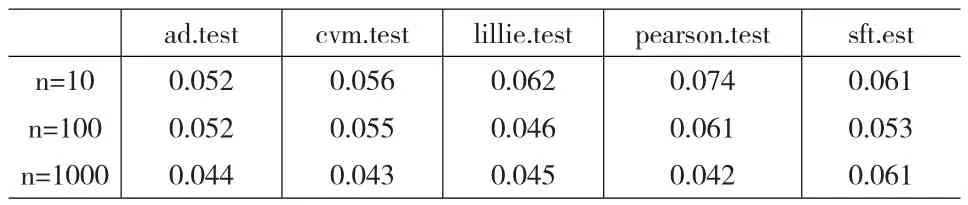
表1 判断错误率

我们进行随机模拟的办法抽取简单随机样本X1，X2，…，Xn～H(x) ，其中 H(x)=εΦ(x)+(1-ε)Φ(，我们取 ε=0.9 ，样 本 量 n=10，100，1000 ，以 及 k=3，10，30，100分别对得到的样本做ad正态性检验。我们得到了图2：

对于不同的样本量，观测不同的k值的影响：

从图1中看出在样本量较小(n=10)的情况下,lillie检验和pearson检验的p值均值较大,但是pearson检验错误率很高，其他检验的错误较低,同时p值的均值较大。说明在小样本的情况下,pearson检验不够稳定,我们可以选用其他4个检验较好。在样本量较大(n=100,1000)的情况下,pearson检验的p值均值较小,并且错误率也较高(在n=100时0.061),sf检验的错误率也比较高(在n=1000时,0.061),所以在样本量较大时,选用ad检验、cvm检验、lillie检验较好。

2.2 当样本来自混合正态总体

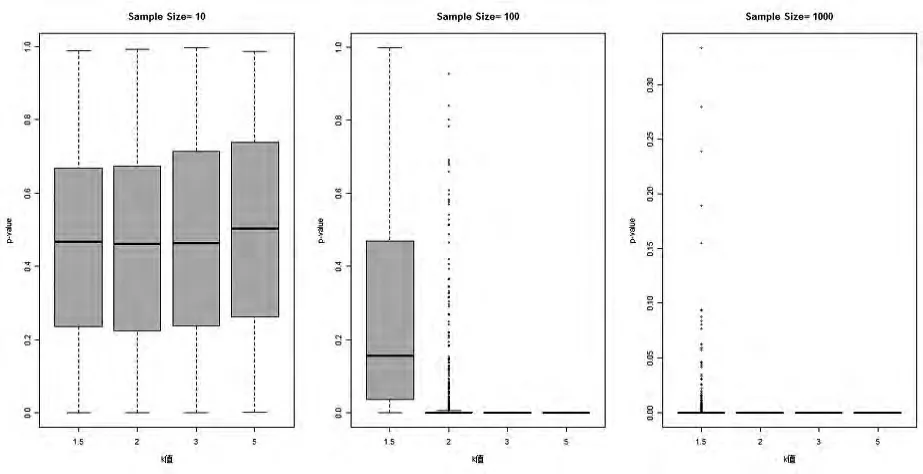
图2 不同样本量ad正态性检验箱线图

对于不同的k值，观测不同样本影响：

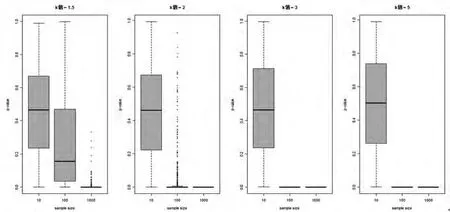
图3 不同的k值ad正态性检验箱线图

从图2和图3发现:

对于样本量比较小n=10,无论k值大小,在ad检验下样本多数为正态,而对于样本量较大的情况(n=100，1000),除了k=1.5，n=100的情况下检验基本上都拒绝零假设,也就是样本并不从正态总体中得到。所以我们对该问题有如下结论：

当样本量较小时,无论k值的大小,该混合正态模型在ad检验下都服从正态总体。

当样本量较大时,如果k值较小(k在1到3之间),那么混合正态模型在ad检验下也一定依概率服从正态总体,如果k值较大(大于3),那么该混合正态模型在ad检验下基本上不符合正态总体。

2.3 当样本来自t分布总体

对t分布的渐近性质进行随机模拟的检验。从总体中抽取样本量为n=100的简单随机样本 X1，X2，…，Xn～t(d)我们对于自由度分别为d=5，10，…，100用ad检验做正态性检验,得到图4:(x轴为不同的自由度,y轴为对应的p值)。

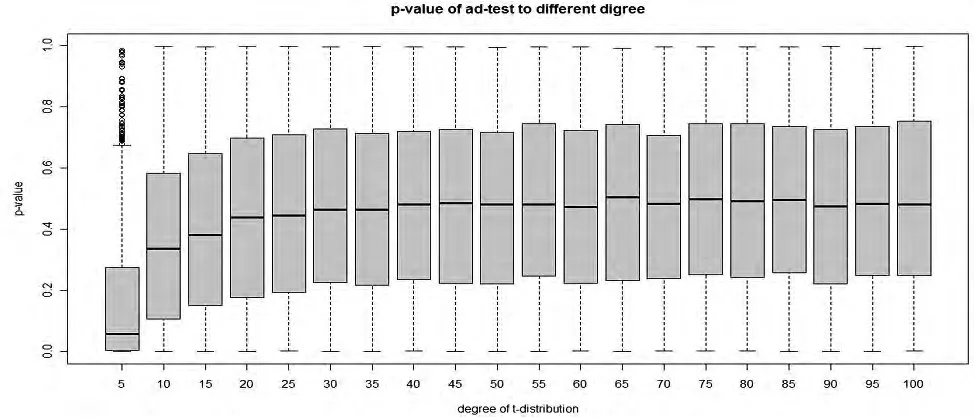
图4 d=5，10，…，100时ad正态性检验箱线图

于是我们对自由度d=5，6，…，20重复上面的步骤,得到图5：(x轴为不同的自由度,y轴为对应的p值)。

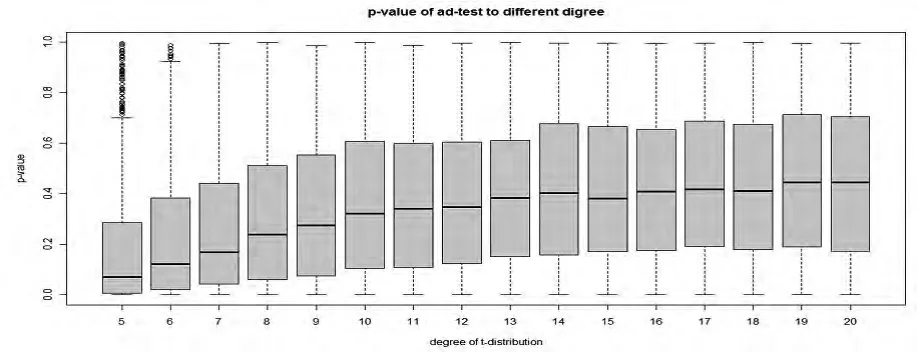
图5 d=5，6，…，20时ad正态性检验箱线图

我们可以从图5看出当自由度d较小(小于等于20)的时候,该样本（从t分布中抽取）并不能在ad检验下服从正态分布，而当自由度d较大(大于20)的时候,该样本可以认为是从正态总体中得到。

3 结论

本文介绍了正态性检验的原理及概述了几个常用的正态性检验方法，并在取不同样本量的情况下通过随机模拟的方法，分别计算得到五种检验方法的p值并作出箱线图。而且分别考虑了当样本来自正态总体、混合正态总体以及t分布总体的情况下各检验方法的特点。并得到如下结论：

（1）在样本量较小(n=10)的情况下,当样本来自正态总体时，lillie检验和pearson检验的p值均值较大,但是pearson检验错误率很高，其他检验的错误较低,同时p值的均值较大。说明在小样本的情况下,pearson检验不够稳定,我们可以选用其他4个检验较好。在样本量较大(n=100,1000)的情况下,pearson检验的p值均值较小,并且错误率也较高(在n=100时0.061),sf检验的错误率也比较高(在n=1000时,0.061),所以在样本量较大时,选用ad检验、cvm检验、lillie检验较好。

（2）当样本量较小时,无论k值的大小,混合正态模型在ad检验下都服从正态总体；当样本量较大时,如果k值较小(k在1到3之间),那么混合正态模型在ad检验下也一定依概率服从正态总体,如果k值较大(大于3),那么该混合正态模型在ad检验下基本上不符合正态总体。

（3）当自由度d较小(小于等于20)的时候,样本（从t分布中抽取）并不能在ad检验下服从正态分布。而当自由度d较大(大于20)的时候,样本可以认为是从正态总体中得到。

[1] 章刚勇，阮陆宁.基于Monte Carlo随机模拟的几种正态性检验方法的比较[J].统计与决策,2011,(7).

[2] Anderson T W,Darling D A.A Test of Goodness of Fit[J].Journal of The American Statistical Association,1954,（49）.

[3] Anderson T W,Darling D A.Asymptotic Theory of Certain Goodness of Fit Criteria Based on Stochastic Processes[J].Annals of Mathemati⁃cal Statistics,1952,(23).

[4] Stephens M A.EDF Statistics for Goodness of Fit and Some Compari⁃sons[J].Journal of The American Statistical Association,1974,(69).