基于模糊信息粒化SVM时序回归CPI预测

路世昌，赵博琦，毕建武

0 引言

消费者物价指数(CPI)，是以与居民生活有关的产品及劳务等价格统计出来的综合指标，可用来衡量物价的变动情况[1]。CPI涉及经济发展，关乎社会和谐，维系人民生计，是管理者制定宏观经济政策、分析货币市场和债券市场及央行公开市场业务的重要参考依据，历来备受政府和民众关注。因此对CPI的精确预测具有重要的现实意义[2]。然而CPI受到多种不确定因素影响，很难对其进行非常精确的预测，这时对CPI变化范围及走势进行预测显得更为重要。模糊信息粒化能够通过群体中个体之间的协作和信息共享来寻找最优解，降低维数，加快拟合收敛。支持向量机(SVM)有优良的泛化能力，并且在解决小样本、非线性及高维空间表现出了很多的优势，能够避免灾难维数，局部极值等问题。本文将模糊信息粒化方法与支持向量机相结合，提出了基于模糊信息粒化SVM时序回归CPI预测模型，该模型能够给出CPI较精确的变化范围及走势，为经济政策以及宏观经济决策提供依据。

1 模糊信息粒化支持向量机模型

1.1 模糊信息粒化

信息粒化就是将一个整体分解为一个个的部分进行研究，每个部分为一个信息粒。信息粒就是一些由于难以区别、或相似接近或具备某种功能而结合在一起的元素的集合。L.A.Zadeh于1979年在模糊集合论的基础上首次提出并讨论了模糊信息粒化问题，并给出了一种数据里的命题刻画[3～5]：

gΔ=(x is G)is λ

其中，x是论域U中取值的变量，G是U的模糊子集，由隶属函数μG来刻画。λ表示可能性概率。一般假设U为实数集合R，G是U的凸模糊子集，λ是单位区间的模糊子集。

模糊信息粒就是以模糊集形式表示信息粒。在对时间序列进行模糊粒化时主要包括划分窗口和模糊化两个步骤。其中模糊化是最为关键的部分，也就是在所给窗口上建立一个能取代原来窗口信息的模糊集。本文采用的是W.Pcdrycz粒化方法[6]。该方法基本思想：

⑴模糊粒子能够合理代表原始数据；

⑵模糊粒子要有一定的特殊性。

为找到两者最佳平衡，可建立如下函数：

QA=MA/NA

其中MA为满足⑴，NA为满足⑵。

本文采用三角形模糊粒子，其隶属函数如下；

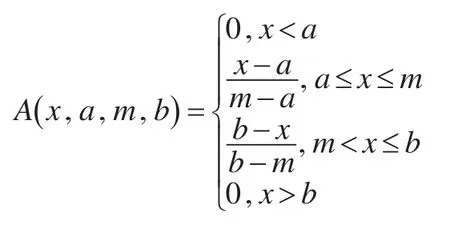
Low,R,Up为模糊粒子的三个参数，对于三角型模糊数而言，分别代表a,m,b三个参数。其中Low描述原始数据变化的最小值，R反映变化的平均水平，Up则表示原始数据变化的最大值。

1.2 支持向量机[7～10]

支持向量机是20世纪90年代由Vapnik等提出的一种研究小样本、小概率事件的神经网络模型,能够根据有限的样本信息在模型的复杂性和学习能力之间寻求最优解。与神经网络相比，支持向量机是基于统计学习理论的小样本学习方法，采用结构风险最小化原则，具有很好的泛化性能；而神经网络是基于大样本的学习方法，采用经验风险最小化原则。基本思想：通过非线性映射将原空间映射至高维特征空间，将搜索到的最优线性回归超平面问题转化为求解凸约束下的凸规划问题。

支持向量机的基本想是通过事先确定的非线性映射将输入向量映射的一个高维特征空间(Hilbert空间)，然后在此高维空间中再进行回归。

首先将输入量x通过映射Φ:Rn→H映射到高维特征空间H中用函数

f(x)=ω·Φ(x)+b

拟合数据(xi,yi)目标函数式为：

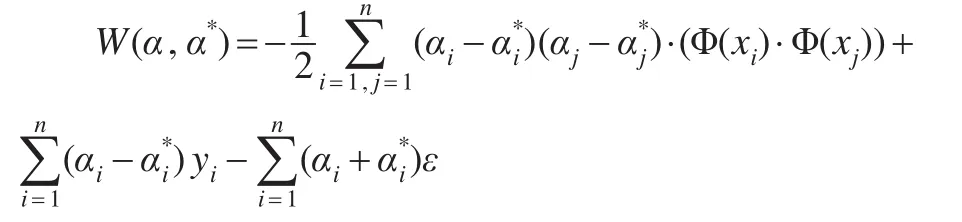
式中涉及到高维特征空间点积运算Φ(xi)·Φ(yi)，而且函数Φ是未知的，高维的。支持向量机理论只考虑高维特征空间的点积运算K(xi,yi)=Φ(xi)·Φ(yi)，而不直接使用函数Φ。称K(xi,yi)为核函数，核函数的选取应使其为高维特征空间的一个点积，核函数的类型有多种，本文选取径向基核函数：

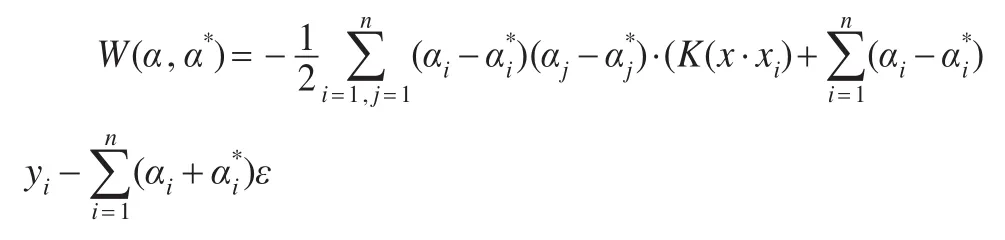
得可求得合函数的表示式为：

1.3 模糊信息粒化支持向量机CPI预测模型

模糊信息粒化支持向量机CPI预测流程如下：

（1）获取历年CPI数据，并进行输入；

（2）对CPI数据进行模糊信息粒化处理；

（3）采用交叉验证的方法，利用模糊粒化处理后的数据对SVM进行训练确定最优参数c和g；

（4）利用最优c和g建立模糊信息粒化SVM模型对CPI进行预测；

（5）输出CPI变化趋势及变化空间。

模型流程图如下：

图1 模型流程图

2 实证分析

本文以2000年1月份到2014年1月份月度CPI为研究对象，其中2013年11月之前的数据用于建立模型，之后的数据用于模型检验。数据来源于国家统计局官方网站。序列时序图见图2。

图2 CPI序列时序

2.1 模糊信息粒化处理

本文将3个月的CPI作为一个窗口大小，得窗口数目为原始数据长度除以3后取整。在Matlab 2012a环境下进行模糊粒化处理结果见图3。

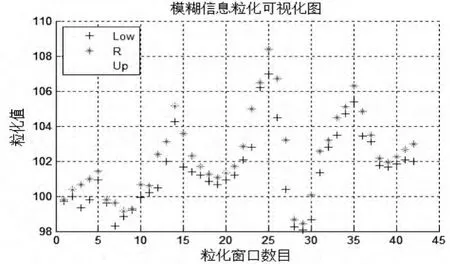
图3 模糊粒化效果

2.2 利用SVM对模糊粒化数据进行预测

在Matlab 2012a环境下利用SVM对三个模糊粒子Low,R,Up进行回归预测，将原始数据归一化到[0，1],采用交叉验证对SVM进行参数寻优，结果如下：

Low：交叉验证 MSE=0.0116525，Best c=2，Best g=0.125；

R：交叉验证MSE=0.0670537，Best c=4，Best g=0.125；

Up：交叉验证 MSE=0.0683058，Best c=5.65685，Best g=0.125

利用最优参数进行拟合及预测，三个模糊粒子Low,R,Up拟合结果见图4，预测结果见表1。

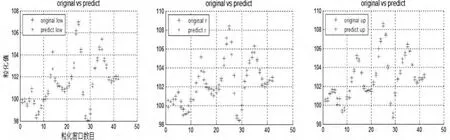
图4 信息粒化拟合结果

表1 预测结果及比较

由表1可知本文预测的CPI变化范围是准确的，精确度较高，而且可以看出这三个月CPI数值整体呈略微下降趋势。表明该模型预测结果可靠，能够为相关决策提供依据，具有一定的实用性。

3 结论

⑴将模糊信息粒化模型与SVM相结合，提出了提出了基于模糊信息粒化SVM回归CPI预测模型，该模型能够综合利用模糊信息粒化及SVM的优点。利用该模型进行实际预测，预测结果变化范围及变化趋势与实际相符，证明了该模型的有效性和实用性。

⑵该模型是基于历史CPI数据建立的，没有考虑经济变化，物价水平等各种不确定性因素，模型还有待于进一步完善。

[1] 郭晓峰.基于ARIMA模型的中国CPI走势预测分析[J].统计与决策,2012,(11).

[2] 韩春蕾,高婉君.我国月度CPI的组合预测及分析[J].统计与决策,2014,(1).

[3] 张铃，张钹.模糊商空间理论(模糊粒度计算方法)[J].软件学报,2003,14(4).

[4] 张蕾，周洲.基于小波和信息粒化的BP神经网络的轴承故障诊断[J].机械科学与技术，2012,31(1).

[5] Bargiela A,Pedrycz W.Granular Computing:An Introduction[M].Dodrecht:Kluwer Academic Publishers,2003.

[6] MATLAB中文论坛.MTALAB神经网络30个案例分析[M].北京：北京航空航天大学出版社，2010.

[7] Nello Cristianini John Shawe-Talor.支持向量机导论[M].（李国正,王猛,曾华军译）.北京:电子工业出版社，2004.

[8] Cao L J.Support Vector Machines Experts for Forecasting[J].Neuro⁃computing,2003,(51).

[9] Chen L.Hourly Water Demand Forecast Model Based on Support Vec⁃tor Machine[J].Journal of Basic Science and Engineering,2009,17(4).

[10] 刘希亮,赵学胜,陆锋.基于GA-SVM的露天矿抛掷爆破抛掷率预测[J].煤炭学报,2012,37(12).