直觉正态模糊数Choquet 积分算子及其决策应用

常娟，杜迎雪，刘卫锋

（郑州航空工业管理学院 数学学院，河南郑州, 450046）

0 引言

多属性决策方法（multi-attribute decision method,MADM）可用于解决工程、经济和管理领域中的诸多问题。通常决策属性指标体系应具有独立性、完备性和代表性，但在实际问题中，属性指标体系的独立性常常难以满足。例如，若用价格、性能和售后3个属性指标选择设备，一般来说，性能和售后好的设备价格高，即属性间的权重不满足可加性，若用加权算术平均算子（WA）对属性信息集结，则属性间的关联可抵消各属性的独立贡献[1]。因此，对属性间存在关联的MADM 问题的研究具有重要的理论和现实意义。1974 年，SUGENO[2]首次提出模糊测度的概念，MARICHAL[3]通过对模糊测度的研究，提出属性间的关联均可用模糊测度度量。而基于模糊测度的Choquet 积分[4-5]可以灵活地体现输入变量间的相互关联情况。因此，利用模糊测度和Choquet积分解决属性间有关联的MADM 问题，这一方法广受关注。其中文献[1,6-7]研究了在实数情况下属性信息有关联的MADM 方法，并用于解决实际问题。随后研究者们相继开展了对属性间具有关联性的模糊MADM 问题研究。其中，高岩等[8]利用Choquet 积分构造了非线性规划模型，提出一种直觉模糊MADM 方 法；XU[9]和TAN 等[10-11]基 于Choquet 积分的直觉模糊数和区间直觉模糊数构造了关联信息集成算子，并研究这些算子的性质，TAN 等[11]提出了基于Choquet 积分的逼近理想解排序（technique for order preferences by similarity to an ideal solution,TOPSIS）法，用于解决区间直觉模糊信息的MADM 问题；曲国华等[12]则结合模糊测度、Choquet 积分和Shapley 值，提出了改进的直觉模糊TOPSIS 法；王坚强 等[13]、万树平 等[14]研究基 于Choquet 积分的直觉三角模糊数的决策方法和集成算子，并分别给出了利用优化模型确定模糊测度的方法；陶长琪等[15]、周晓辉等[16]分别提出了基于Choquet 积分的直觉模糊数、区间直觉梯形模糊数信息集成算子，并给出了具体的决策方法。

考虑现实生活中大量随机现象服从或近似服从正态分布，1996 年，YANG 等[17]定义了正态模糊数，指出正态模糊数在刻画模糊信息时更接近人类思维，也更为准确[18]。在模糊MADM 问题中，可以借助数理统计的方法，给出正态模糊数形式的属性信息。然而，单纯用正态模糊数表示属性值，则暗含决策者对这一信息是完全认可的，无法反映决策者对这一信息的信任程度和犹豫程度。而直觉模糊集的隶属度、非隶属度和犹豫度可细致刻画决策者的支持、反对和中立三种态度。因此，结合直觉模糊集的思想，王坚强等[19]在正态模糊数基础上增加了隶属度和非隶属度信息，并定义了直觉正态模糊数。目前，有关直觉正态模糊数的研究成果主要有：王坚强等[19-20]定义了直觉正态模糊数的运算、距离、得分函数和精确函数，提出直觉正态模糊数加权算术平均算子和诱导广义有序加权平均算子；刘政敏等[21]则给出了不同于文献[19]的直觉正态模糊数的运算法则，定义了直觉正态模糊数的期望值，并提出了准则间具有优先关系的直觉正态模糊数集成算子；常娟等[22]提出了权重由集结数据确定的直觉正态模糊数幂均算子；文献[23-24]则定义了区间直觉正态模糊数的运算，并给出了区间直觉正态模糊数的一些集成算子，如有序加权几何平均算子、连续有序加权几何平均算子、诱导有序加权平均算子和诱导有序加权几何平均算子。

上述关于直觉正态模糊数的集成算子均是基于属性间相互独立的情形下展开的讨论，而在实际决策问题中，属性间往往是相互关联的。因此，研究属性间的关联性且属性值为直觉正态模糊数的MADM 问题，具有重要的理论和实际意义。为此，在文献[22]定义的直觉正态模糊数运算基础上,利用模糊测度λ，将Choquet 积分用于直觉正态模糊数，构建直觉正态模糊数Choquet 积分平均（INFCA）算子和直觉正态模糊数Choquet 积分几何（INFCG）算子，详细探讨其性质和特殊形式。此外，通过构建线性规划模型，提出一种确定各属性子集模糊测度λ的方法，进而给出基于直觉正态模糊Choquet 积分算子的MADM 方法。最后，通过实例验证该方法的可行性和有效性。

1 相关概念

1.1 直觉正态模糊数

若正态 模糊数=(a,σ),则由定 义2，得E()=a,D()=。在实际问题中，可借助数理统计方法得到正态模糊数形式的属性信息。例如，对某一实验参数进行100 次观测，经计算,样本均值和标准差分别为0.669 0 和0.059 5，即a=0.669 0，=0.059 5，σ=0.084 1,则可用正态模糊数(0.669 0,0.084 1)表示该参数的观测值。通过对正态模糊数添加隶属度和非隶属度，王坚强等[19]提出了直觉正态模糊数。

定义3[19]设(a,σ)∈,称A=〈(a,σ),μA,νA〉为直觉正态模糊数，其隶属函数和非隶属函数分别为

1.2 模糊测度和Choquet 积分

定义7[2]设P(X)为有限集X的幂集,映射ψ:P(X)→[0,1]满足条件：

（1）ψ(∅)=0,ψ(X)=1;

（2）若X1，X2∈P(X)，X1⊆X2，则ψ(X1)≤ψ(X2)，称ψ为X上的模糊测度。

为提高模糊测度计算的可行性，SUGENO 又提出了λ模糊测度。

定义8[2]给定λ∈(-1,∞),P(X)为有限集X的幂集，设映射gλ:P(X)→[0,1]满足条件：

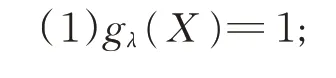
定义9[5]若f为定义在X={x1,x2,…,xn}上的非负函数，ψ为X上的模糊测度，则f关 于ψ的 离散Choquet 积分为

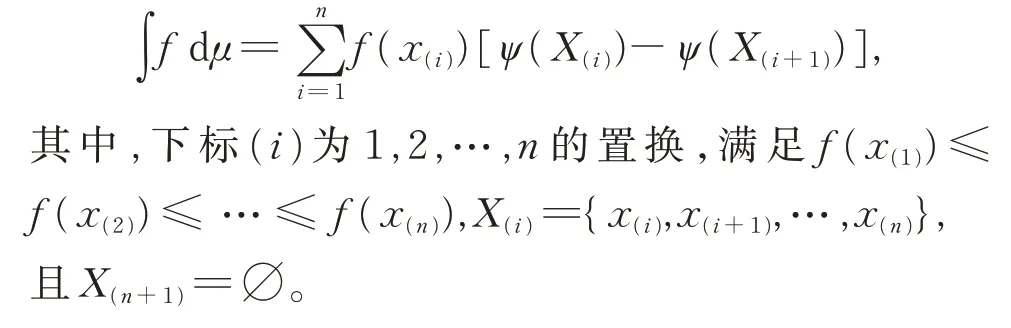
2 直觉正态模糊数Choquet 积分算子

基于模糊测度的Choquet 积分可以体现输入信息间的关联情况，鉴于此，为解决属性间关联的直觉正态模糊数MADM 问题，根据直觉正态模糊数的运算法则和Choquet 积分的定义，构造直觉正态模糊数Choquet 积分算子。

2.1 INFCA 算子

定义10设X={x1,x2,…,xn},定义在X上的直觉正 态模糊数组Ai=〈(ai,σi),μi,νi〉(i=1,2,…,n),ψ为X上的模 糊测度,Ai关 于ψ的离散Choquet 积分为

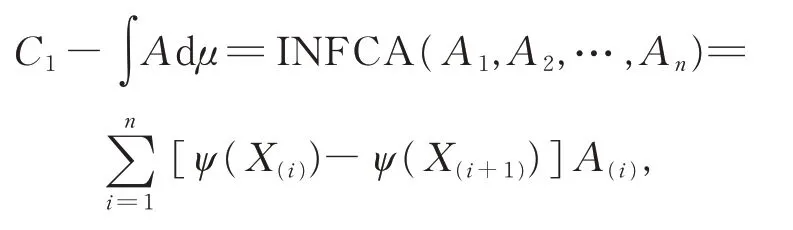
则称INFCA 为直觉正态模糊数Choquet 积分平均算子，简称INFCA 算子。其中下标(i)为1,2,…,n的置换，满 足A(1)≤A(2)≤…≤A(n),X(i)={x(i),x(i+1),…,x(n)},且X(n+1)=∅。

定理1设定义在X上的直觉正态模糊数Ai=〈(ai,σi),μi,νi〉,i=1,2,…,n,ψ为X上的模糊测度，则INFCA(A1,A2,…,An)∈Ω,且INFCA(A1,A2,…,An)=

INFCA 算子的基本特点是：对直觉正态模糊数A1,A2,…,An按升序排列后进行加权关联集成，将属性子集的模糊测度差ψ(X(i))-ψ(X(i+1))作为集成时的位置权重，其与Ai无关。

INFCA 算子具有以下性质：

定 理 2设一组 正态模糊数Ai=〈(ai,σi),μi,νi〉,i=1,2,…,n,ψ为X上的模糊测度。其具有以下性质

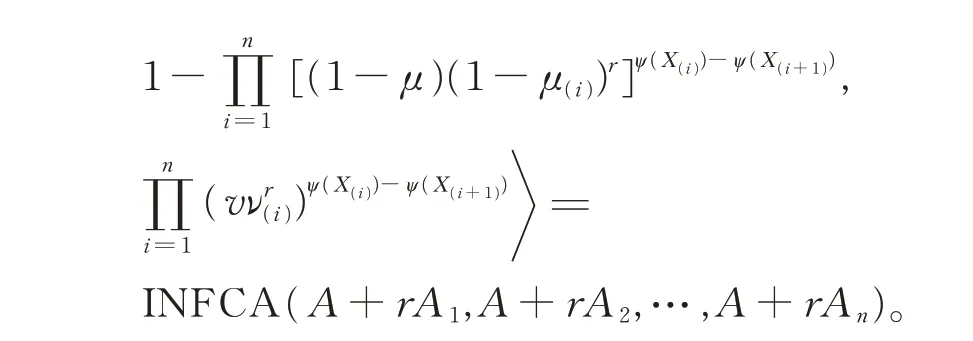
当X上的模糊测度ψ比较特殊时，INFCA 算子具有以下特殊形式：

（1）若对任意Y∈P(X),且Y≠∅，有ψ(Y)=1,则INFCA(A1,A2,…,An)=max {Ai};

（2）若对任意Y∈P(X),且Y≠X，有ψ(Y)=0,则INFCA(A1,A2,…,An)=min {Ai};

（3）若对任 意Y∈P(X),有ψ(Y)=,则

此时，INFCA 算子即为直觉正态模糊数加权平均（INFWA）算子；

（4）设(w1,w2,…,wn)为INFOWA 算子的权重向量，Y∈P(X),且|Y|为Y 中的元素个数，若对任意Y∈P(X),ψ(Y)=,有

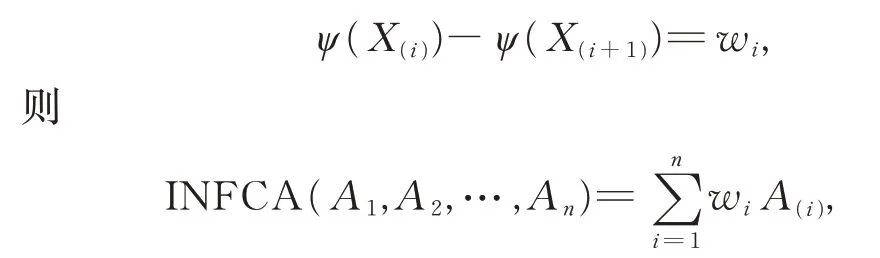
此时，INFCA 算子即为直觉正态模糊数有序加权平均（INFOWA）算子。

2.2 INFCG 算子

定义11设X={x1,x2,…,xn},定义在X上的直觉正 态模糊 数Ai=〈(ai,σi),μi,νi〉,i=1,2,…,n,ψ为X上的模 糊测度,Ai关 于ψ的离散Choquet 积分：

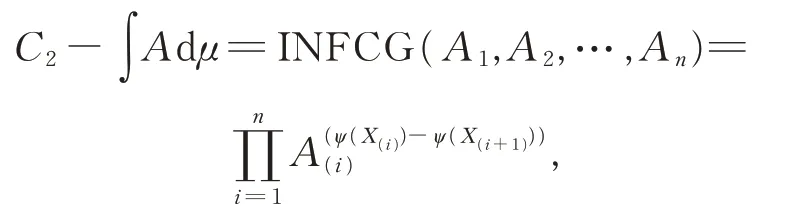
则称INFCG 为直觉正态模糊数Choquet 积分几何算子，简称INFCG 算子。其中下标(i)为1,2,…,n的置换，满 足A(1)≤A(2)≤…≤A(n),X(i)={x(i),x(i+1),…,x(n)},且X(n+1)=∅。

定理3设定义在X上的直觉正态模糊数Ai=〈(ai,σi),μi,νi〉,i=1,2,…,n,ψ为X上的模糊测度，则INFCG(A1,A2,…,An)∈Ω,且

同理，当X上的模糊测度ψ比较特殊时，INFCG算子具有以下特殊形式：

（1）若对任意Y∈P(X),且Y≠∅，有ψ(Y)=1,则INFCG(A1,A2,…,An)=max {Ai};

（2）若对任意Y∈P(X),且Y≠X，有ψ(Y)=0,则INFCG(A1,A2,…,An)=min {Ai};

（3）若对任 意Y∈P(X),有ψ(Y)=,则

INFCG(A1,A2,…,An)=,

此时，INFCG 算子即为直觉正态模糊数加权几何平均（INFWG）算子。

（4）设(w1,w2,…,wn)为INFOWG 算子的权重向量，Y∈P(X),且|Y|为Y 中元素的个数，若对任意Y∈P(X),ψ(Y)=,有

此时，INFCG 算子即为直觉正态模糊数有序加权几何（INFOWG）算子。

3 决策应用

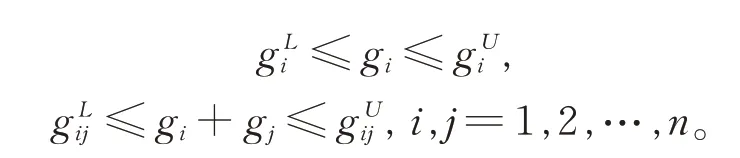
通过求解以上优化模型可得各属性指标的λ模糊测度gi,i=1,2,…,n,再利用1+λ=确定参数λ的值，从而由定义8 可计算各属性子集的λ模糊测度。

以下为基于INFCA（或INFCG）算子的直觉正态模糊数多属性决策方法的具体步骤：

步骤1确定直觉正态模糊数决策矩阵(Aij)m×n。

步骤2规范化决策矩阵[19]。

步骤3计算各属性指标的λ模糊测度,以确定各属性子集的λ模糊测度。

步骤4利用INFCA（或INFCG）算子对各方案的属性值进行集结，得到综合属性值。

步骤5利用定义6 对各方案的综合属性值从大到小进行排序，得到最优方案。

例1某制造公司在选择供应商时，有4 个考核指标：供货能力(u1)、交易能力(u2)、售后服务(u3)、企业实力(u4)，均为效益型指标，显然，u1，u2，u4这3 个指标之间存在冗余关联。设gλ(ui)=wi,i=1,2,3,4，表示各属性指标的重要程度，经专家评定，满足以下条件：0.1≤w1≤0.3,0.2≤w2≤0.4,0.3≤w3≤0.4,0.2 ≤w4≤0.4,0.3 ≤w1+w2≤0.4。现有4个供应商A1,A2,A3,A4,邀请多位相关领域专家，对各供应商进行实地考察，并对各指标的满意度进行打分（10 分制）。经计算,供应商A1在供货能力u1下所得平均分为3，标准差为0.282 8，由定义2,打分结果可用正态模糊数（3,0.4）表示，考虑专家对此结果的认可程度，对每位专家对正态模糊数（3,0.4）的接受程度再进行投票，若接受比例为0.7，不接受比例为0.2，则A1在u1下的指标值最终可通过直觉正态模糊数〈(3,0.4),0.7,0.2〉表示。类似地，可得到其他各项指标值，具体如表1 所示。最后筛选出最优供应商。

步骤1规范化决策矩阵，如表2 所示。

表1 直觉正态模糊数决策矩阵Table 1 Intuitive normal fuzzy numbers decision matrix

表2 直觉正态模糊数规范化决策矩阵Table 2 Intuitive normal fuzzy numbers normalized decision matrix

步骤2计算各属性子集的模糊测度。

首先，通过线性规划模型：

步骤3利用INFCA 算子对规范化后各方案的属性值进行集结：

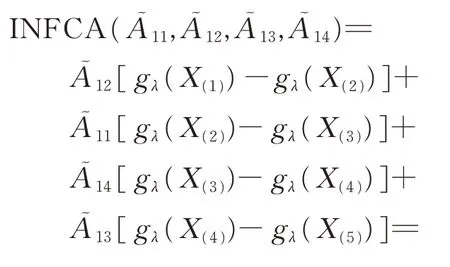
步骤4计算以上各方案综合指标值的得分函数,分别得到0.317 0,0.523 2,0.375 9,0.726 8,则各供应商的排序结果为A4≻A2≻A3≻A1,最优供应商为A4。

文献[19，22]在不考虑属性关联情况下分别利用TOPSIS 法和幂均算子法（λ=2），得到的排序结果均为A4≻A2≻A1≻A3，与本文方法得到的最优供应商为A4一致。表1 的数据也表明，A4的各项指标值占绝对优势，决策结果是合理的，但A1,A3的排序发生了变化。可见，考虑指标间存在关联性这一实际情况，确实会对排序结果产生影响。

4 结语

针对属性间存在关联性这一实际情况，笔者利用模糊测度和Choquet 积分，构造了INFCA 算子和INFCG 算子，经研究，这些算子具备较好的性质且具有一些特殊形式。在具体的多属性决策问题中，如何确定各属性子集的模糊测度，本文也给出了具体方法。实例结果表明，本文的决策方法是可行和有效的,符合直觉正态模糊信息的决策问题属性间的关联性，是对现有的直觉正态模糊理论成果的补充和完善。