沥青混凝土心墙风化料坝三维地震响应分析
2015-07-25谢庆明江守燕曹庆明杜成斌
谢庆明 江守燕 曹庆明 杜成斌
(1.云南省水利水电勘测设计研究院,昆明 650021;2.河海大学 力学与材料学院,南京 210098)
1 工程概况
轿子山水库地处昆明市东川区红土地镇境内,位于金沙江流域小江左岸一级支流小清河中游,属金沙江水系二级支流.水库距东川区约76km,距红土地镇约12km,距昆明市233km.轿子山水库坝址以上控制径流面积145km2,多年平均径流量17 917万m3.轿子山水库枢纽由拦河大坝、溢洪道、泄洪隧洞和输水隧洞组成.拦河大坝设计为沥青混凝土心墙风化料坝,其典型剖面如图1所示,坝顶轴线长320m,最大坝高99.0m,坝顶高程2 204.00m;水库正常蓄水位2 201.50m,死库容315万m3,兴利库容1 635万m3,总库容2 033万m3.
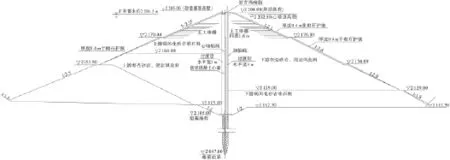
图1 大坝典型剖面
轿子山水库工程为综合利用水利工程,供水任务为:解决集镇供水、乌龙灌区和绿茂灌区农田灌溉供水以及工业供水的综合利用水库工程.根据国家相关标准[1],工程等级为Ⅲ等,工程规模为中型.永久性主要建筑物拦河大坝坝高超过70m,其建筑物级别提高一级,为2级建筑物,洪水标准不提高,其它主要建筑物溢洪道、导流泄洪隧洞、输水隧洞等建筑物按3级设计,次要建筑物按4级设计,临时性导流建筑物按4级设计.水库防洪标准按50年一遇洪水设计,1 000年一遇洪水校核,消能防冲按30年一遇洪水设计.水库工程区地震动峰值加速度为0.3g(50年超越概率10%的坝址区基岩地震加速度峰值),地震动反应谱特征周期0.40s,相应地震基本烈度为VIII度,工程按VIII度地震设防.
本文基于大型商业有限元软件ABAQUS,并利用ABAQUS平台提供的UMAT子程序接口开发了等效线性模型,结合本实际工程,分析该沥青混凝土心墙风化料坝的地震响应,为大坝的抗震安全评价提供依据.
2 计算模型及计算参数
2.1 材料动力本构模型
针对不同的材料特性,计算中主要采用了两种材料本构模型:线弹性模型和等效线性模型.
1)线弹性模型.计算中,对于基岩、帷幕采用线弹性本构模型进行计算.
2)等效线性模型.坝壳砂岩泥岩强弱风化料、弱风化砂岩堆石料、沥青混凝土以及过渡料采用等效线性模型.在等效线性模型中,土体的剪切模量G和阻尼比λ是剪切应变γ的函数,在土石坝地震响应分析中采用南科院沈珠江院士提出的如下模型[2]
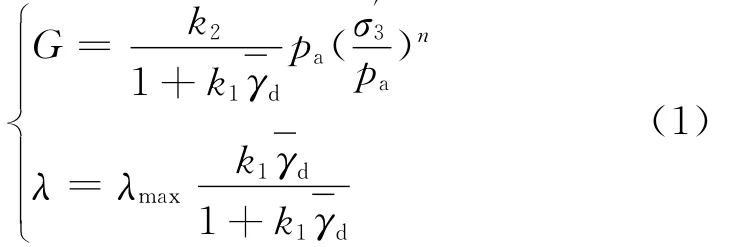
式(1)中第1式还可表达为:


2.2 残余变形计算方法
地震永久变形分析是在完成土石坝静力分析和动力分析的基础上进行的[3-4],动力残余体积应变增量Δεv和残余剪切应变增量Δγs可按下式计算

式中,Δε为残余体应变增量;Δγ为残余剪应变增量;γd为动应变幅值;S1为应力水平,S1=τ/τf;N和 ΔN为振动次数及其增量;c1、c2、c3、c4、c5为土石料动力变形试验参数.
动应变幅值和残余应变随着动应力幅值的增大而明显增大,但垂直向动应变幅值是不均匀的,一般开始几周较大,后期略有减小.在整理试验结果时,以第10次循环的幅值为准.动力残余变形包括残余体积应变εvr和残余剪切应变γr,后者主要发生在不等向固结试样中,等向固结试样中有时也会出现少量残余剪应变,但其值较小,在整理成果时可将其忽略不计.残余应变的发展大体上符合半对数衰减规律,但初期的体积应变衰减慢于半对数规律,而剪切应变衰减则初期快、后期慢.体积应变初期读数较小的原因,似与孔隙水来不及排出有关,因而实际情况可能更接近于半对数规律.总的说来,半对数曲线仍是描述残余变形发展趋势的一个较好选择.设cvr和cdr分别为各试验曲线在半对数坐标上的斜率,则残余应变为
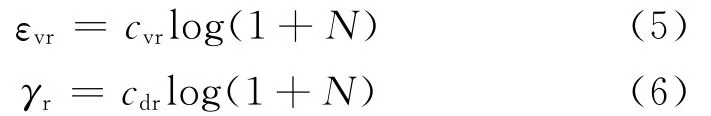
式中,cvr和cdr还应该是动应力比Rd和固结应力比Kc的函数,用动剪应变幅值γd代替动应力比Rd,用剪应力比或应力水平S1=τ/τf代替Kc,可使表达更为清晰.即有

等向固结时,S1=0,故式(7)、(8)分别退化为cvr=c1和cdr=0.以往的研究表明,不同应力比(应力水平)对cvr影响很小,故可假定S1对cvr无影响,即式(7)中的c3=0.由式(7),对在cvr~γd的双对数关系曲线进行线性拟合,c1即为γd=1%处的直线截距,c2即为拟合直线的斜率.根据式(8),对cdr/S1~γd的双对数关系曲线进行线性拟合,c4即为γd=1%处的直线截距,c5即为拟合直线的斜率,其中应力水平S1根据静三轴试验结果求取.当以10为底的对数整理参数时,c1和c4要乘0.434 3.
2.3 坝体材料参数
1)线弹性材料参数
基岩、帷幕的材料参数见表1.

表1 线弹性材料参数
2)等效线性模型材料参数
坝壳砂岩泥岩强弱风化料、弱风化砂岩堆石料、沥青混凝土以及过渡料采用等效线性模型本构模型,材料最大动剪切模量参数取值根据该坝坝料的动力试验结果确定及参照冶勒水电站大坝的参数取值[5-6],堆石料的动泊松比νd一般在0.3~0.4之间变化,计算取为0.33,考虑到沥青混凝土的孔隙率较低,动力泊松比较大,取νd=0.45,具体见表2,材料剪切模量比及阻尼比与最大剪应变关系曲线如图2所示.
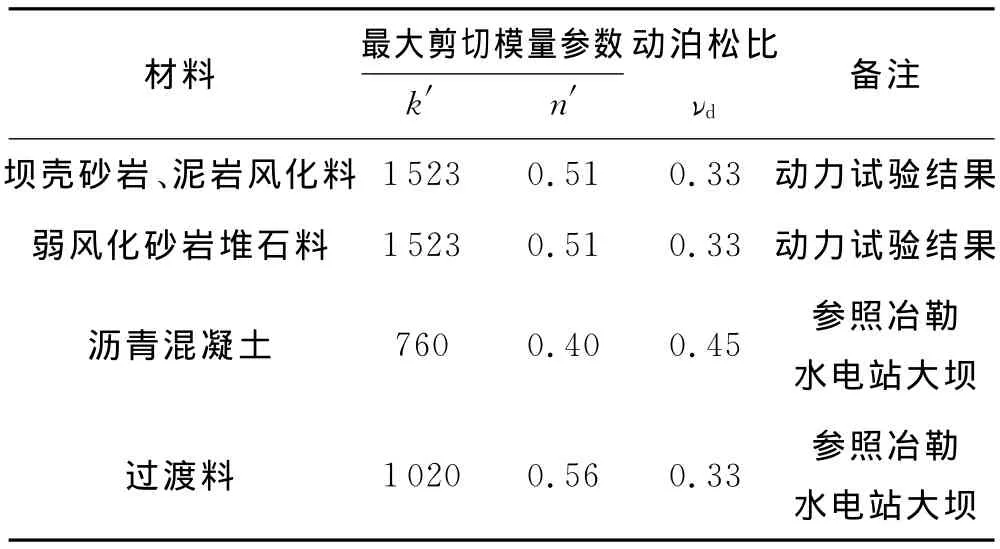
表2 材料最大剪切模量参数
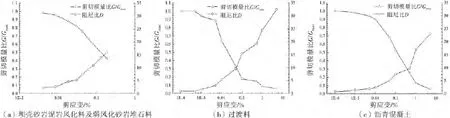
图2 材料剪切模量比及阻尼比与最大剪应变关系曲线
3)残余变形材料参数
坝料的残余变形参数见表3,坝壳砂岩泥岩风化料、弱风化砂岩堆石料残余变形参数由南京水利科学研究院坝料的动力残余变形试验提供.
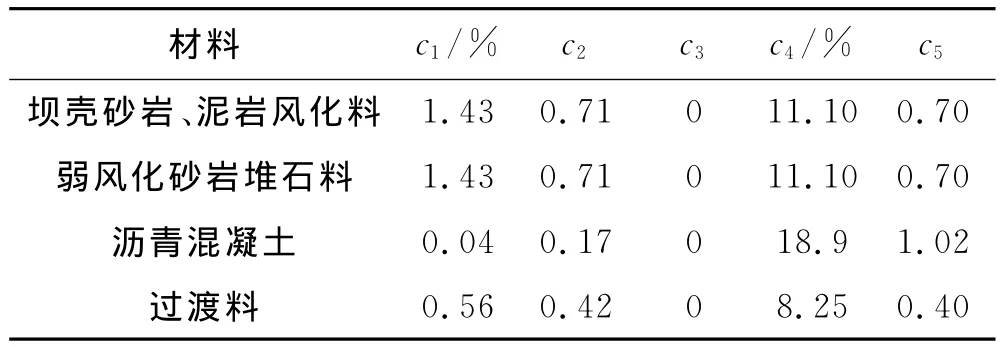
表3 材料残余变形参数
2.4 基岩地震动时程
动力响应是指坝体在正常蓄水位高程2 201.50m时遭遇地震时的动力响应.计算采用的地震波由云南省地震工程研究院提供的50年超越概率10%的3条坝址区基岩地震加速度时程,加速度峰值为0.3g.根据现行规范[7],同时计入顺河流方向的水平向与竖向地震作用,顺河向地震加速度峰值为0.3g,竖向地震加速度峰值取为顺河向的2/3并按规范规定乘以0.5的遇合系数,地震波加速度时程曲线如图3所示.地震持续时间为20s,时间间隔为0.02s.
3 三维有限元仿真计算
3.1 三维有限元模型
计算中采用的三维有限元计算网格如图4所示.在三维有限元分析中绝大多数单元为8结点六面体单元,为适应坝体形状变化及协调材料分区,在边界处布置了少量的楔形体单元.选取的坐标系x方向顺河流向(指向下游为正),z方向正向竖直向上,y方向垂直xz平面按右手坐标系确定(横河向,正向由右岸指向左岸).坝体和地基系统共有63 066个结点,62 234个单元,其中坝体包括14 610个结点和13 252个单元.基岩范围沿上、下游分别延伸约2倍最大坝高,向基础深部延伸约2倍最大坝高.基岩边界上施加适当的边界条件消除整体大坝的刚体位移.

图3 输入的地震波加速度时程曲线

图4 三维有限元计算网格
3.2 计算结果及分析
1)加速度响应
图5给出了由地震波3计算得到的坝横0+120.0m剖面加速度极值分布,图6给出了由地震波3计算得到的坝横0+140.0m剖面加速度极值分布,图7给出了由地震波3计算得到的坝横0+180.0 m剖面加速度极值分布,图8给出了不同地震波下加速度放大倍数沿坝顶分布.由计算结果可看出,顺河向加速度随高程增加而增大,加速度最大值发生在坝顶处.竖直向加速度不仅由坝基向坝顶逐渐增加,而且在同一高程处,大体表现出了由坝内向坝坡方向逐渐增大的趋势,竖直向加速度最大值约发生在上游坝坡近坝顶处.3种地震波下坝顶顺河向加速度最大放大倍数分别为:4.50、3.70、3.76,3种地震波下坝顶竖直向加速度最大放大倍数分别为:3.65、3.30、4.34.在地震作用下,坝顶、上下游坝坡近坝顶等位置有可能会有坝料松动、滑落的可能性,建议在上述区域采取适当的抗震加固措施.
2)动剪应力响应
三维计算结果表明动剪应力响应量以τzx最大,τxy次之,τyz最小(x为顺河流向,y为横河向),因此本文给出了部分剖面τzx的极值分布.表4列出了不同地震波下坝体动剪应力τzx最值计算结果,图9给出了由地震波3计算得到的心墙及坝体部分剖面(坝横0+120.0m剖面、坝横0+140.0m剖面、坝横0+180.0m剖面)动剪应力τzx的极值分布.

图5 坝横0+120.0m剖面加速度极值分布
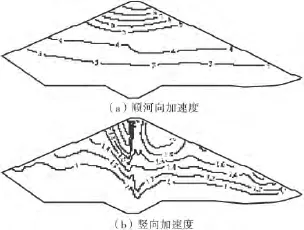
图6 坝横0+140.0m剖面加速度极值分布
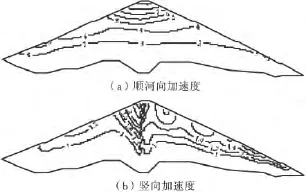
图7 坝横0+180.0m剖面加速度极值分布

图8 加速度放大倍数沿坝顶分布
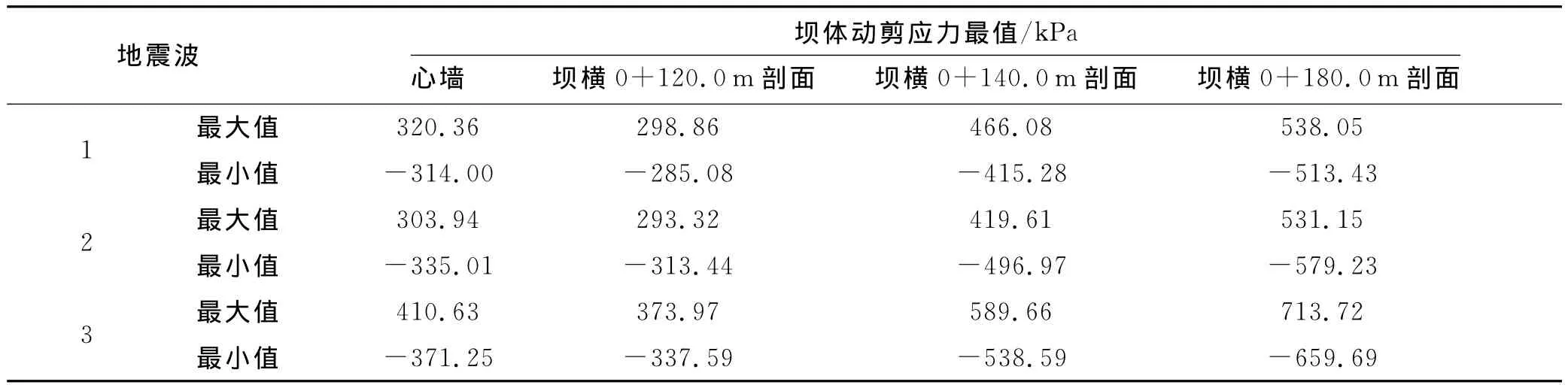
表4 坝体动剪应力最值计算结果
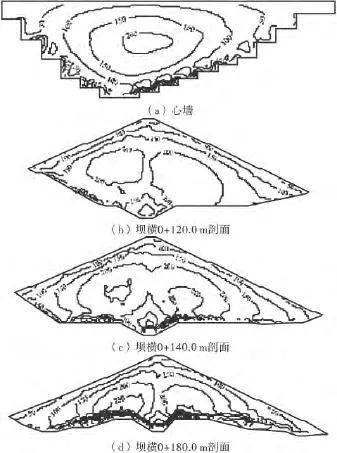
图9 心墙及坝体动剪应力τzx极值分布/kPa
从计算结果看,心墙墙面动剪应力较小,3种地震波计算得到的最大值为410.63kPa,最大值约发生在坝横0+120.0m剖面~坝横0+180.0m剖面的心墙部分且位于心墙总高的1/2位置处.从3个典型剖面动剪应力的计算结果看,各剖面动剪应力在靠近坝面处较小,坝面大部分区域的动剪应力约200kPa左右,而距离坝面越远,动剪应力越大,在靠近坝基附近达到最大,原因是基岩刚度较大,约束了坝体的变形,使得动剪应力响应增大.总体来说,心墙及坝体的动剪应力不是很大,分布较均匀,不会出现剪切破坏.
3)动位移响应
表5列出了典型剖面(坝横0+120.0m剖面、坝横0+140.0m剖面、坝横0+180.0m剖面)动位移极值计算结果.图10给出了由地震波3计算得到的坝横0+120.0m剖面动位移极值分布,图11给出了由地震波3计算得到的坝横0+140.0m剖面动位移极值分布,图12给出了由地震波3计算得到的坝横0+180.0m剖面动位移极值分布.
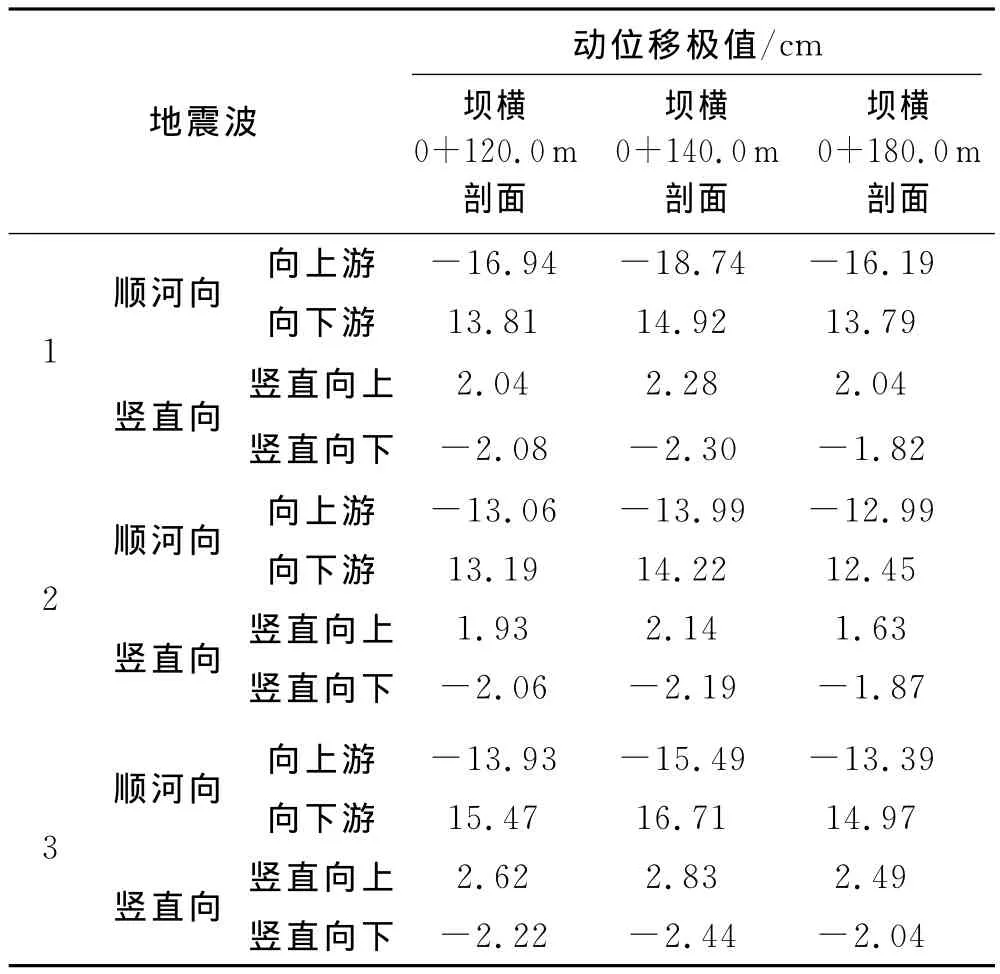
表5 典型剖面动位移极值计算结果
由计算结果可看出,顺河向动位移最大值发生在坝顶处,竖直向动位移最大值发生在下游坝坡靠近坝顶处.各典型剖面中,以坝横0+140.0m剖面的动位移响应最激烈,3种地震波下顺河向动位移最大值分别为18.74cm(向上游)、14.22cm(向下游)、16.71 cm(向下游),3种地震波下竖直向动位移最大值分别为2.30cm(竖直向下)、2.19cm(竖直向下)、2.83cm(竖直向上).
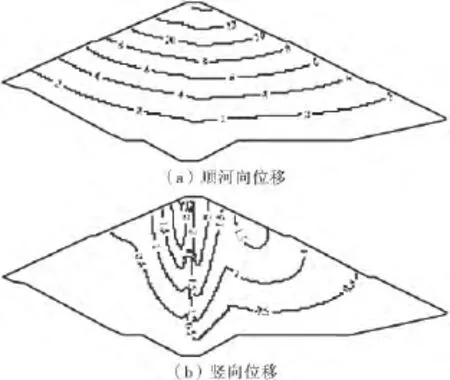
图10 坝横0+120.0m剖面动位移极值分布(cm)
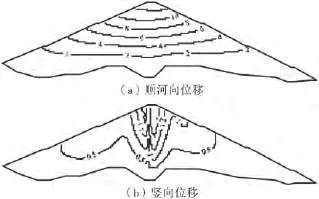
图11 坝横0+140.0m剖面动位移极值分布(cm)

图12 坝横0+180.0m剖面动位移极值分布(cm)
4)地震永久变形
表6列出了典型剖面(坝横0+120.0m剖面、坝横0+140.0m剖面、坝横0+180.0m剖面)地震永久变形最值计算结果.
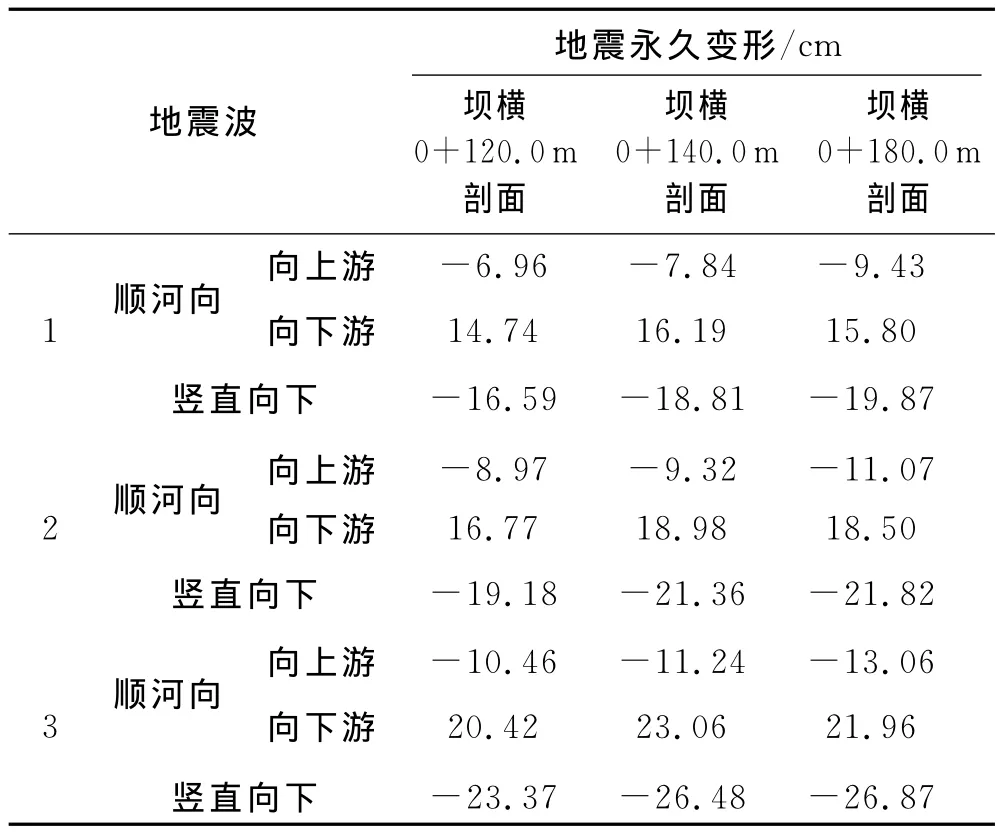
表6 典型剖面地震永久变形最值
图13给出了由地震波3计算得到的坝横0+120.0m剖面地震永久变形分布,图14给出了由地震波3计算得到的坝横0+140.0m剖面地震永久变形分布,图15给出了由地震波3计算得到的坝横0+180.0m剖面地震永久变形分布.
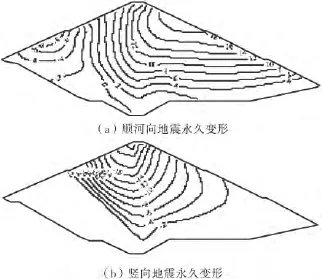
图13 坝横0+120.0m剖面地震永久变形分布(cm)
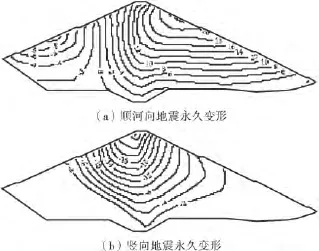
图14 坝横0+140.0m剖面地震永久变形分布(cm)

图15 坝横0+180.0m剖面地震永久变形分布(cm)
由计算结果可以看出,地震顺河向永久变形以向下游为主,各剖面顺河向永久变形最大值均发生在下游坝坡的中上部,以坝横0+140.0m剖面的响应最激烈,3种地震波下坝横0+140.0m剖面向下游的顺河向地震永久变形最大值分别为:16.19cm、18.98 cm、23.06cm.竖直向地震永久变形以竖直向下为主,随着高程的增大,地震永久变形增大,各剖面竖直向地震永久变形最大值发生在坝顶靠近上游坝坡的一侧,以坝横0+180.0m剖面的响应最激烈,3种地震波下坝横0+180.0m剖面竖直向下地震永久变形最大值分别为:19.87cm、21.82cm、26.87cm,坝体地震沉陷量为最大坝高的0.20%、0.22%、0.27%.可以看出,坝体在地震中的沉陷比水平位移大,体现了堆石体在高固结应力和循环荷载作用下的残余体积变形特性.
与国内外类似工程相比较,如:
1)糯扎渡直心墙土石坝[8],最大坝高261.5m,输入地震加速度峰值为2.83m/s2,最大水平地震永久变形发生在下游坝坡的中上部,最大竖向地震永久变形发生在坝顶靠近上游坝坡的一侧,且分布规律与本文计算结果非常一致.
2)瀑布沟土石坝[9],最大坝高188m,输入地震加速度峰值为2.0m/s2,最大水平地震永久变形发生在坝顶部位,最大竖向地震永久变形发生在水位线与坝体上游坝壳交界处(坝顶靠近上游坝坡的一侧),且分布规律与本文计算结果也非常一致.
3)水牛家心墙堆石坝[10],最大坝高108m,输入地震加速度峰值为2.9m/s2,最大水平地震永久变形发生在坝顶部位,最大竖向地震永久变形发生在坝顶靠近上游坝坡的一侧.
4)下坂地沥青混凝土心墙坝[11],最大坝高78m,输入地震加速度峰值为3.09m/s2,顺河向最大地震永久变形为20.4cm,竖直向最大地震永久变形为38.3cm.
5)黄金坪沥青混凝土心墙堆石坝[12],最大坝高81m,输入地震加速度峰值为4.78m/s2,地震后大坝竖向永久变形由坝基向坝顶逐渐增大,由两岸向河床方向逐渐增大,上游侧堆石区的变形大于下游侧,整个大坝竖向永久变形的最大值为53.0cm,坝体地震沉陷量为坝高的0.66%.通过与类似工程的对比分析可见,本文计算得到的地震永久变形分布规律、最大值发生的位置及变形值都是合理的.
4 主要结论
基于大型商业有限元软件ABAQUS,并利用ABAQUS平台提供的UMAT子程序接口开发了等效线性模型,结合本实际工程,分析该沥青混凝土心墙风化料坝的地震响应,有限元分析计算得出以下几点结论:
1)顺河向加速度随高程增加而增大,加速度最大值发生在坝顶处.竖直向加速度不仅由坝基向坝顶逐渐增加,而且在同一高程处,大体表现出了由坝内向坝坡方向逐渐增大的趋势,竖直向加速度最大值约发生在上游坝坡近坝顶处.3种地震波下坝顶顺河向加速度最大放大倍数分别为:4.50、3.70、3.76,3种地震波下坝顶竖直向加速度最大放大倍数分别为:3.65、3.30、4.34.在地震作用下,坝顶、上下游坝坡近坝顶等位置有可能会有坝料松动、滑落的可能性,建议在上述区域采取适当的抗震加固措施.
2)心墙墙面动剪应力较小,3种地震波计算得到的最大值为410.63kPa,最大值约发生在坝横0+120.0m剖面~坝横0+180.0m剖面的心墙部分且位于心墙总高的1/2位置处.动剪应力在靠近坝面处较小,坝面大部分区域的动剪应力约200kPa左右,而距离坝面越远,动剪应力越大,在靠近坝基附近达到最大,原因是基岩刚度较大,约束了坝体的变形,使得动剪应力响应增大.总体来说,心墙及坝体的动剪应力不是很大,分布较均匀,不会出现剪切破坏.
3)大坝顺河向动位移最大值发生在坝顶处,竖直向动位移最大值发生在下游坝坡靠近坝顶处.各典型剖面中,以坝横0+140.0m剖面的动位移响应最激烈,3种地震波下顺河向动位移最大值分别为18.74 cm(向上游)、14.22cm(向下游)、16.71cm(向下游),3种地震波下竖直向动位移最大值分别为2.30cm(竖直向下)、2.19cm(竖直向下)、2.83cm(竖直向上).
4)地震顺河向永久变形以向下游为主,顺河向永久变形最大值发生在下游坝坡的中上部,以坝横0+140.0m剖面的响应最激烈.
3种地震波下坝横0+140.0m剖面向下游的顺河向地震永久变形最大值分别为:16.19cm、18.98 cm、23.06cm.竖直向地震永久变形以竖直向下为主,随着高程的增大,地震永久变形增大,竖直向地震永久变形最大值发生在坝顶靠近上游坝坡的一侧,以坝横0+180.0m剖面的响应最激烈,3种地震波下坝横0+180.0m剖面竖直向下地震永久变形最大值分别为:19.87cm、21.82cm、26.87cm,坝体地震沉陷量为最大坝高的0.20%、0.22%、0.27%.可以看出,坝体在地震中的沉陷比水平位移大,体现了堆石体在高固结应力和循环荷载作用下的残余体积变形特性.与国内外类似工程相比较,本文计算得到的地震永久变形分布规律、最大值发生的位置及变形值都是合理的.
[1] SL 252-2000.水利水电工程等级划分及洪水标准[S].
[2] 沈珠江,徐 刚.堆石料的动力变形特性[J].水利水运科学研究,1996,6(2):143-150.
[3] 费 康,刘汉龙.ABAQUS的二次开发及在土石坝静、动力分析中的应用[J].岩土力学,2010,31(3):881-890.
[4] 刘汉龙,费 康.考虑残余体应变的土石坝地震永久变形分析[J].岩土力学,2013,34(6):1687-1695.
[5] 王晓东.冶勒水电站大坝心墙与防渗墙连接混凝土基座设计[J].水电站设计,2013,29(2):9-11.
[6] 李永红,王晓东.冶勒沥青混凝土心墙堆石坝抗震设计[J].水电站设计,2004,20(2):40-45.
[7] DL 5073-2000.水工建筑物抗震设计规范[S].北京:中国电力出版社,2001.
[8] 赵剑明,常亚屏,陈宁.高心墙堆石坝地震变形与稳定分析[J].岩土力学,2004,25(2):423-428.
[9] 刘汉龙,陆兆漆,钱家欢.土石坝地震永久变形分析[J].河海大学学报,1996,24(1):91-96.
[10]王玲玲,何蕴龙,费文平.水牛家心墙堆石坝地震永久变形及液化分析[J].岩土力学,2004,25(1):165-168.
[11]王锦峰.下坂地沥青混凝土心墙坝动力反应分析[J].水利与建筑工程学报,2009,7(3):152-154.
[12]嵇红刚.深厚覆盖层上沥青混凝土心墙堆石坝三维动力分析[D].南京:河海大学,2006.
