基于Kriging法的土石坝稳定可靠度分析

许长云

（赣州市天鹰勘测设计有限公司，江西赣州341000）

0 引言

在土木工程领域，可靠度理论最早在结构工程设计中得到应用，后逐渐应用到岩土工程。因为岩土体的物理力学参数的不确定性和离散型，计算坝坡稳定性时不能准确地得到其安全系数，而可靠度理论能够充分考虑其岩土体参数的不确定性，因此可靠度理论在土石坝稳定性分析中得到了快速的发展[1-5]。

统计学原理在研究岩土体参数的不确定性方面有着独特的优势，常用的蒙特卡罗模拟法尽管理论简单清晰，但计算量很大，而Kriging法所需的样本信息少，运用起来灵活，所受限制较少，在研究坝体稳定可靠度方面得到了广泛的应用[6-8]。

基于Kriging法，利用GEOSTUDIO软件中的SLOPE/W模块，结合蒙特卡罗模拟法，分析坝体材料的相关性和变异性对下游坝坡的稳定可靠度的影响。

1 Kriging方法的基本理论

Kriging法被认为是一种改进的线性回归法，Kriging模型的表达式为：

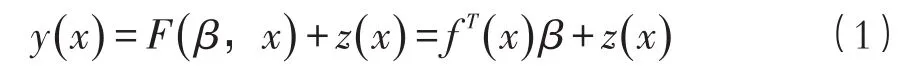
式中：x为某一变量；β为回归系数；z(x)为随机过程；F(β ，x)为Kriging的回归模型

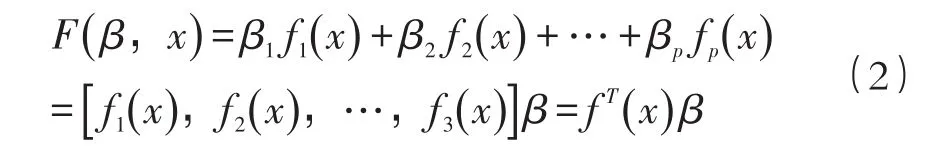
式中：p为多项式个数。

具体的计算过程可参照图1进行，因篇幅有限，对具体拉丁超立方抽样法和Nafa法不做具体介绍。

2 模型的建立及模型参数

某坝坡高16.8 m，坝顶宽6 m，坝坡上游坡比为1∶m=1∶3，坝坡下游坡比为1∶n=1∶2.5。对研究区勘察资料进行整理，选取库岸的某个典型断面进行分析，对坡面进行适当简化，利用GEOSTUDIO建立计算模型，图2为土石坝计算模型。

表1为坝坡相关的物理力学参数，材料采用的是饱和-非饱和渗流模型。

根据上述参数建立Kriging模型，对不同工况下的土石坝进行稳定可靠度分析。根据当地的水文调查，拟采取3种不同的工况进行分析，具体工况如下：

1）工况一：正常蓄水位，水位高h1=12.5 m；

3）工况二：设计洪水位，水位高h2=13 m；

3）工况三：校核洪水位，水位高h3=13.5 m。

在上述3种计算工况中，下游均无水位。

3 坝坡可靠度分析

在GEOSTUDIO软件中，导入SEEP/W模型，对坝体进行渗流分析，得到坝体的浸润线位置，然后将渗流分析结果导入到极限平衡法软件SLOPE/W，采用BISHOP法计算坝体优化安全系数。图3为3种不同工况下下游坝坡渗流稳定性计算结果。

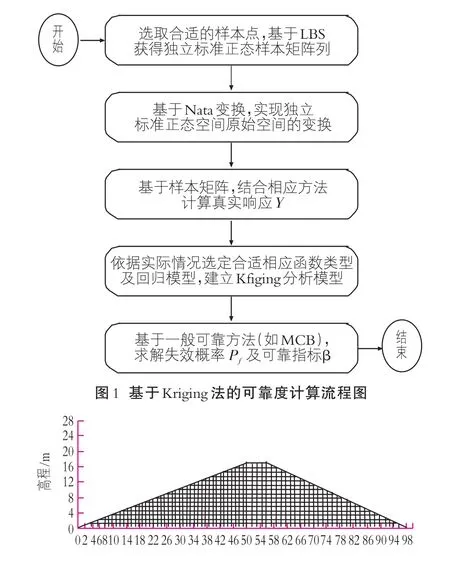
图2 土石坝计算模型

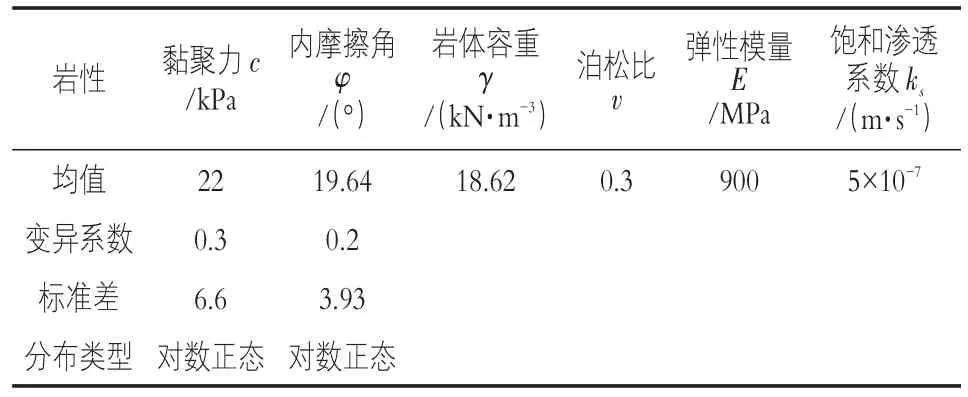
表1 坡体相关物理力学参数

在上述3种不同工况下的渗流稳定性计算中，计算得到的优化安全系数分别为：1.542，1.540，1.492。

按照Kringing法的可靠度分析流程，以黏聚力c和内摩擦角φ为随机变量，选取40个样本点，建立Kriging计算模型，同时，选取10万个样本点，采用蒙特卡罗模拟法（MCS），对不同工况下的下游坝坡进行稳定性分析，将该结果与Kriging法计算结果进行对比。表2为不同工况下的稳定可靠度计算结果。

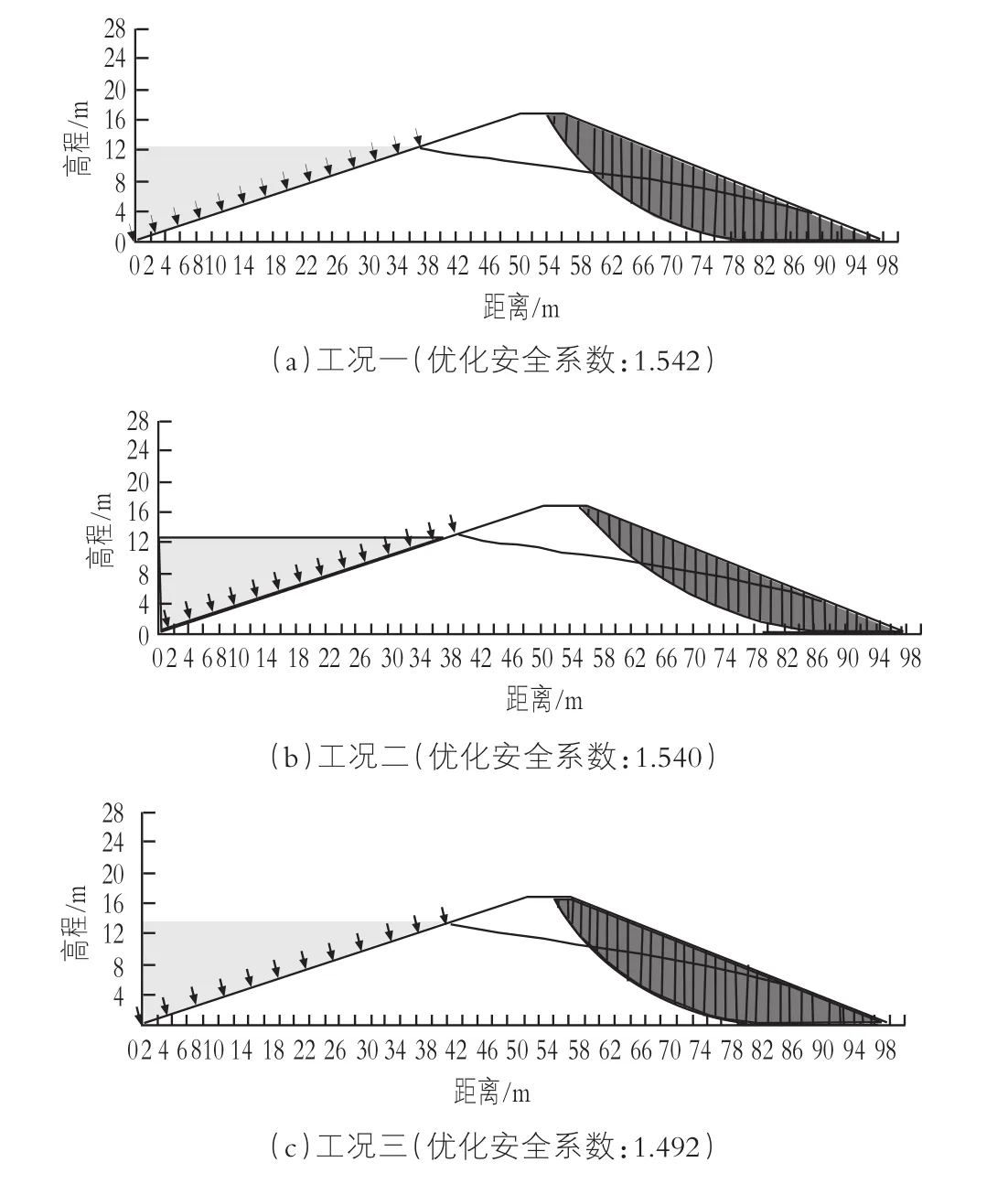
图3 不同工况下下游坝坡渗流稳定性计算结果

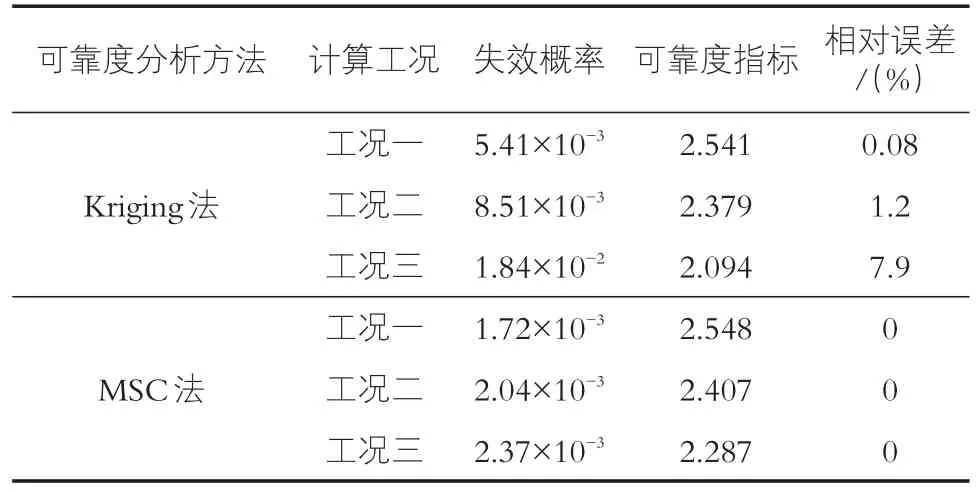
表2 不同工况下下游坝坡稳定可靠度分析结果

从表2中可以看出，随着水位的上升，下游坝坡的失效概率逐渐增加，可靠度指标逐渐降低，水位越高，下游坝坡逐渐不稳定。将Kriging法的计算结果与MSC法计算结果进行对比，3种不同工况下的误差性分别为0.08%，1.2%，7.9%，误差性较低，均在可以接受的范围之内。

4 参数相关性对坝坡稳定性的影响

岩土体的抗剪强度参数中黏聚力c和内摩擦角φ之间存在一定的相关性，选取黏聚力的变异系数为0.3，内摩擦角的变异系数为0.2，选取工况三进行分析，在不改变参数变异系数的情况下，利用Kriging法，对下游坝坡的参数相关性和可靠度之间的关系进行分析，相关系数的变化范围为0.6～-0.6，表3和图3为参数相关性的变化结果。

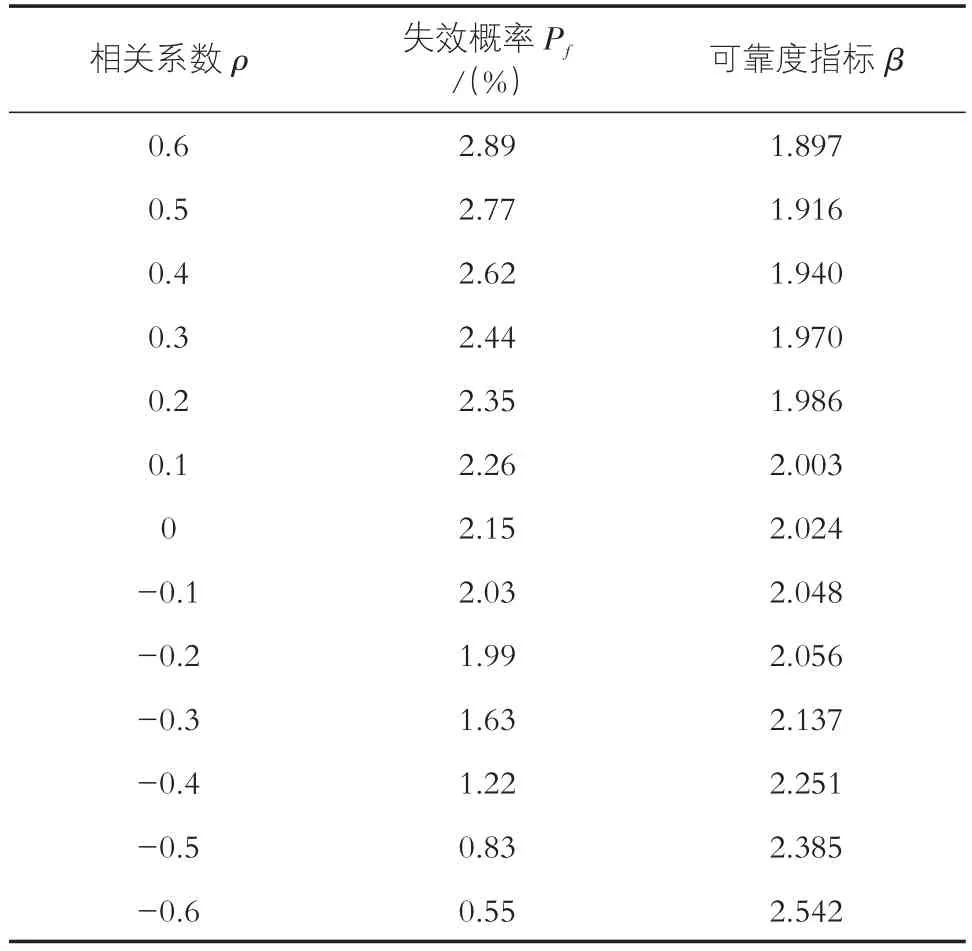
表3 相关性变化结果（工况三）

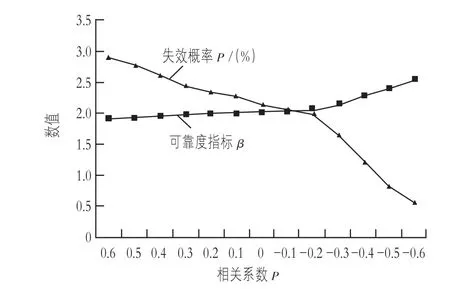
图4 参数相关性变化结果（工况三）

从表3和图4中可以看出，内摩擦角和黏聚力之间正相关性降低，可靠度指标逐渐增加，失效概率逐渐降低，内摩擦角和黏聚力负相关性增加，可靠度指标逐渐增加，失效概率逐渐降低，当相关系数 ρ为-0.2时，失效概率和可靠度指标均发生了突变。内摩擦角和黏聚力之间的负相关性对坝坡的稳定性是有利的，在对坝体稳定性分析时，一定要考虑参数间的相关性。

5 参数变异性对坝坡可靠度的影响

由于岩土体的抗剪强度参数有很大的离散型，其内摩擦角和黏聚力自身有一定的变异性，在上节对参数相关性的分析中，当相关系数为-0.6时，下游坝坡的可靠度指标最大。建立Kriging模型，选取工况三进行分析，拟定内摩擦角和黏聚力的相关系数为-0.6，研究其变异性对下游坝坡可靠度的影响。表4为黏聚力内摩擦角变异系数对下游坝坡稳定性的影响。图5为内摩擦角和黏聚力变异系数对下游坝坡失效概率的影响。图6为内摩擦角和黏聚力变异系数对下游坝坡可靠度指标的影响。

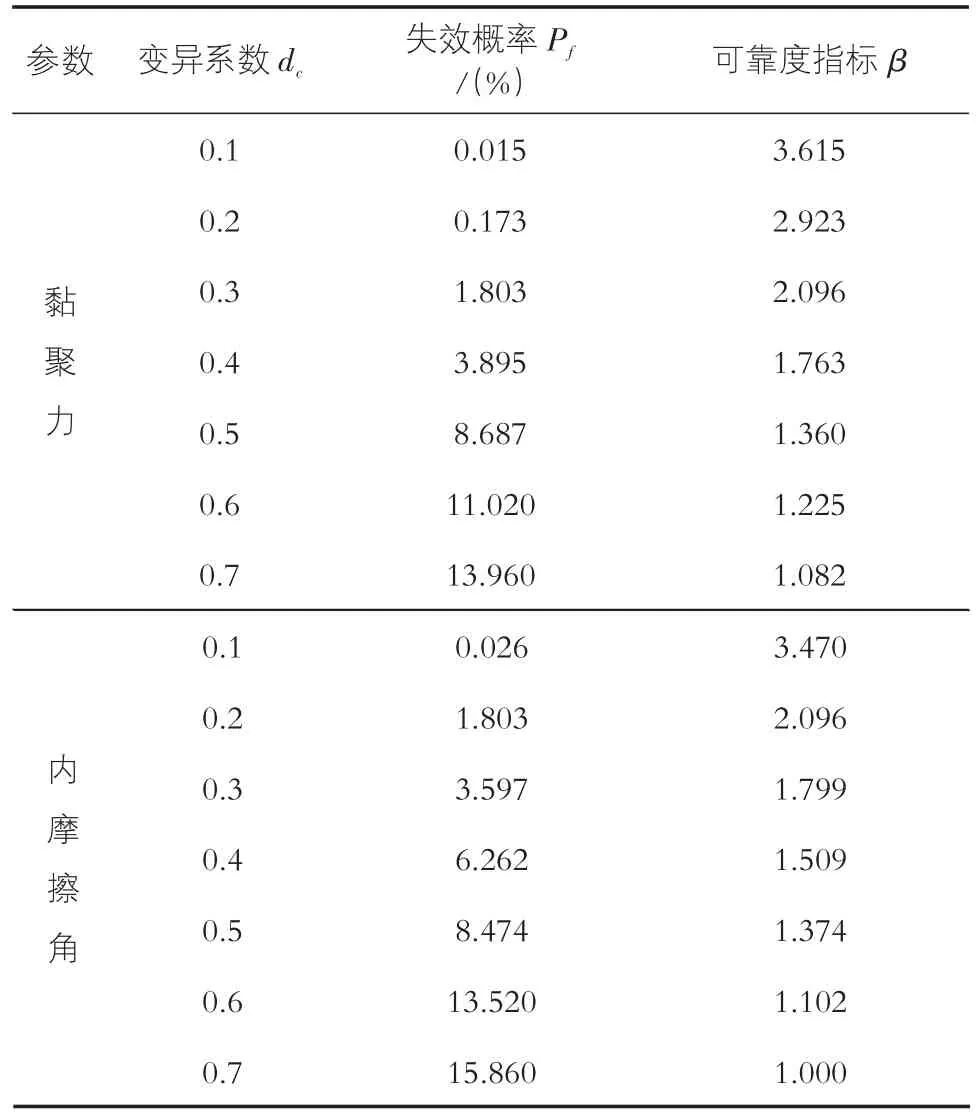
表4 变异系数对下游坝坡稳定性的影响

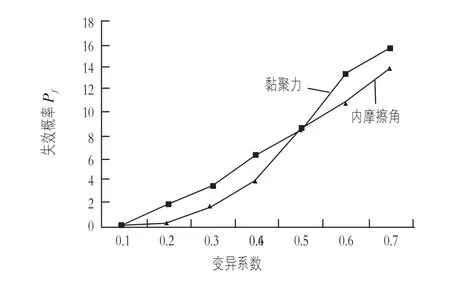
图5 变异系数对下游坝坡失效概率的影响

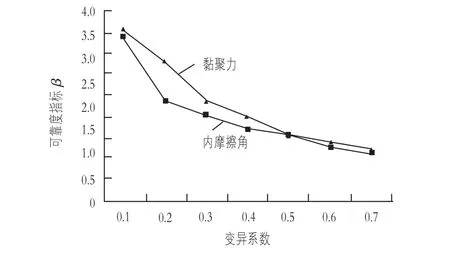
图6 变异系数对下游坝坡可靠度指标的影响

从上述分析结果可知，当坝体内摩擦角和黏聚力相关系数不变时，随着变异系数的增加，下游坝坡的失效概率逐渐增加，可靠度指标逐渐减小，参数变异性越大，对坝体的稳定性越不利，因此，在对坝坡稳定性分析中，应充分考虑参数变异性对稳定可靠度的影响。

6 结论

基于Kriging法，利用GEOSTUDIO软件中的SLOPE/W模块，结合蒙特卡罗模拟法，对下游坝坡的稳定可靠度进行分析。

采用Kriging法对下游坝坡进行稳定性分析，所需数据量少，与蒙特卡罗法相比，计算量低，提高了计算效率。

利用Kriging法对坝坡参数相关性进行分析时，当抗剪强度参数内摩擦角和黏聚力之间呈现正相关性时，随着正相关性的降低，可靠度指标逐渐增加，失效概率逐渐降低，当内摩擦角和黏聚力呈现负相关性时，随着负相关性的增加，可靠度指标逐渐增加，失效概率逐渐降低，参数的负相关性对坝坡稳定性更有利。

利用Kriging法对坝坡参数变异性进行分析时，随着变异系数的增加，下游坝坡的失效概率逐渐增加，可靠度指标逐渐减小，参数变异性越大，对坝体的稳定性越不利。