预应力损失对T梁翼缘板开裂位置影响研究

郑志东

（福州市交通建设集团有限公司，福州 350000）

先简支后连续T梁由于具备简支梁与连续梁桥这两种桥型的优点，在我国20～40m中小跨径桥梁中得到了广泛应用［1－2］.但是，经资料统计及现场调研发现，很多在役简支变连续预应力混凝土T梁桥在不同部位都出现了不同程度的开裂现象，尤其是翼缘板开裂最为严重，而造成T梁开裂的一个重要原因是：受钢束预应力损失的影响，结构的实际应力与设计应力很难完全吻合，计算应力不能很好地反映结构的实际应力状态，过大的结构应力造成混凝土开裂［3］.而我国关于T梁翼缘板开裂的研究很少，尤其是针对预应力损失造成T梁翼缘板开裂位置这个问题研究更少.本文以福建某桥为依托工程，建立Ansys有限元模型，研究钢束的预应力损失对T翼梁缘板应力的影响，分析预应力损失造成T梁翼缘板开裂位置.

1 工程概况

以福建省某3×30m跨径，后张法预制T梁桥为依托工程，选择其中一联中梁，一般构造如图1所示.主梁采用C50混凝土，弹模为3.145×104MPa.预应力钢束采用1860钢绞线，弹模为1.95×105MPa，抗拉强度标准值为1 860MPa，张拉控制应力为1 395 MPa.正弯矩预应力钢束N1、N2、N3规格分别为Φs15.2－8、Φs15.2－9、Φs15.2－9；梁顶负弯矩钢束规格均为Φs15.2－5（4束），T梁预应力钢束布置如图2所示.

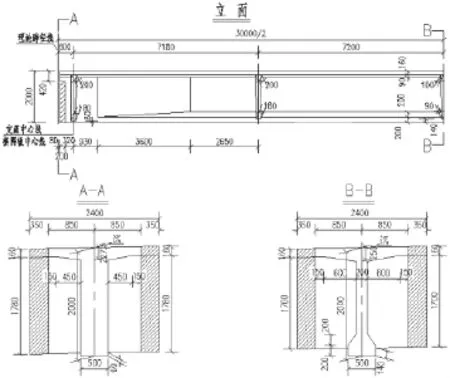
图1 T梁一般构造图

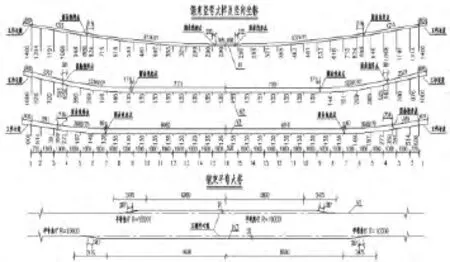
图2 T梁预应力钢束布置图

2 预应力损失相关规定

引起预应力损失的因素主要有：预应力钢筋与管道壁之间的摩擦（σl1）；锚具变形、钢筋回缩和接缝压缩（σl2）；预应力钢筋与台座之间的温差（σl3）；混凝土弹性压缩（σl4）；钢筋松弛（σl5）；混凝土的收缩和徐变（σl6）［4］.其中，后张法构件各阶段预应力损失的组合见表1.

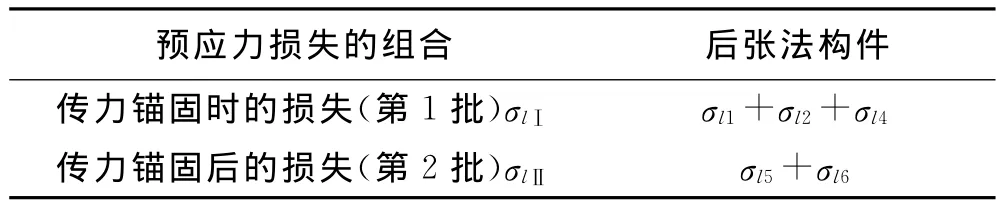
表1 各阶段预应力损失的组合［4］

3 数值分析

3.1 数值模型建立

借鉴嵌入式预应力混凝土组合单元模型的概念，采用SOLID65单元模拟混凝土，同时，将锚下垫板设置成弹性垫块，并采用SOLID45单元模拟，以此避免梁端及顶板负弯矩钢束锚固块因受预应力作用而在未达到极限状态时就因局部拉或压应力过大而发生的破坏［5－6］.梁体有限元模型如图3所示.预应力钢束采用LINK8单元模拟［6］，采用初应变法施加预应力，初应变值为7.13E－4，预应力钢束有限元模型如图4所示.

图3 T梁有限元模型（局部）

图4 预应力钢束有限元模型

3.2 计算工况确立

由于先天设计不足、施工技术不可靠、材料质量存在缺陷等原因，要想保持施加的预应力在理想状态可靠工作基本是不可能的，即预应力损失是无法避免的.根据规范规定计算30mT梁各截面钢束预应力损失值及预加力阶段和使用阶段有效预应力，见表2.从表中可以看出最大预应力损失在使用阶段的支点截面约为19.3%，所以本文选取预应力损失0及20%两个计算工况进行分析.主要分为以下工况：工况Ⅰ：预应力损失0%；工况Ⅱ：预应力损失20%.

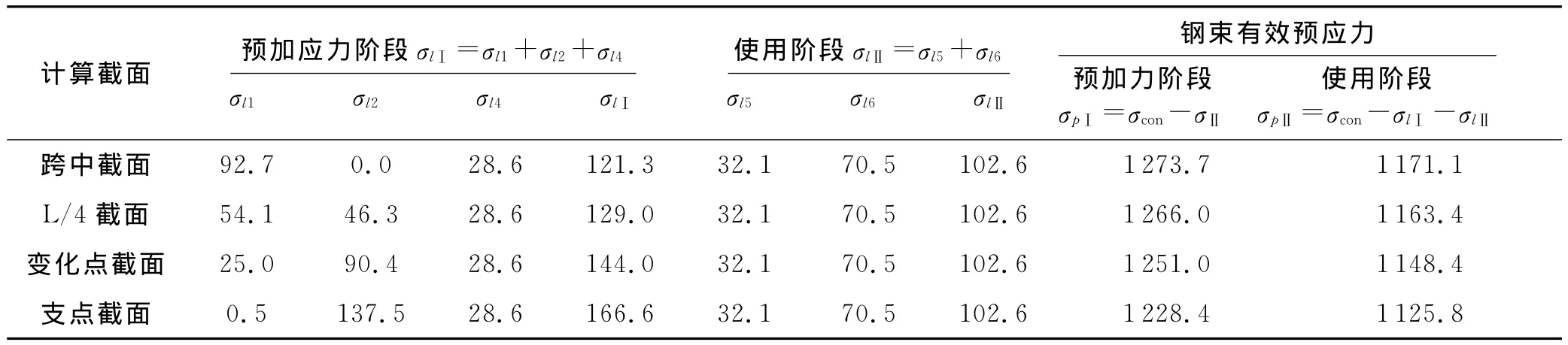
表2 各截面钢束预应力损失值及有效预应力［4］（单位：MPa）

3.3 主要截面及关键点

任意一点的空间应力状态由6个应力分量σx、σy、σz、τxy、τyz、τzx组成，根据最大拉应力强度理论，混凝土的开裂判据为最大主拉应力［7］.在此主要分析T梁截面各部位的第一主应力S1（1st principal stress）沿桥跨方向的分布情况，并规定拉为正、压为负.

选取如图5所示边跨支点（A－A）、边跨跨中（BB）、中跨支点（C－C）、中跨跨中（D－D）截面作为主要计算断面，，并选取合适关键点来反映混凝土的应力状态，如图6所示.

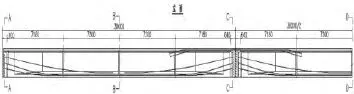
图5 T梁主要截面

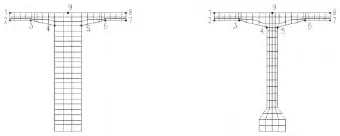
图6 T梁横截面关键点位置

4 预应力损失对翼缘受力性能影响

4.1 边跨支点截面应力计算结果

经计算知各工况下边跨支点A－A截面应力云图及各关键点应力.具体如图7～9及表3所示.

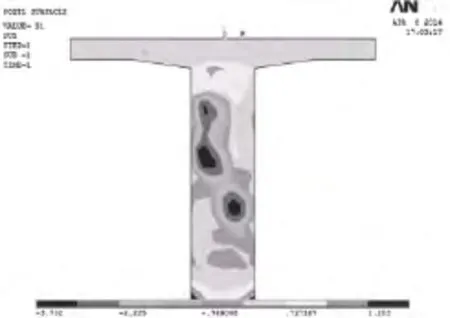
图7 工况Ⅰ，A－A截面应力云图

图8 工况Ⅱ，A－A截面应力云图

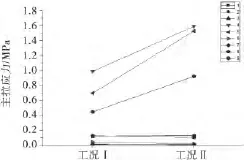
图9 A－A截面关键点应力变化趋势图

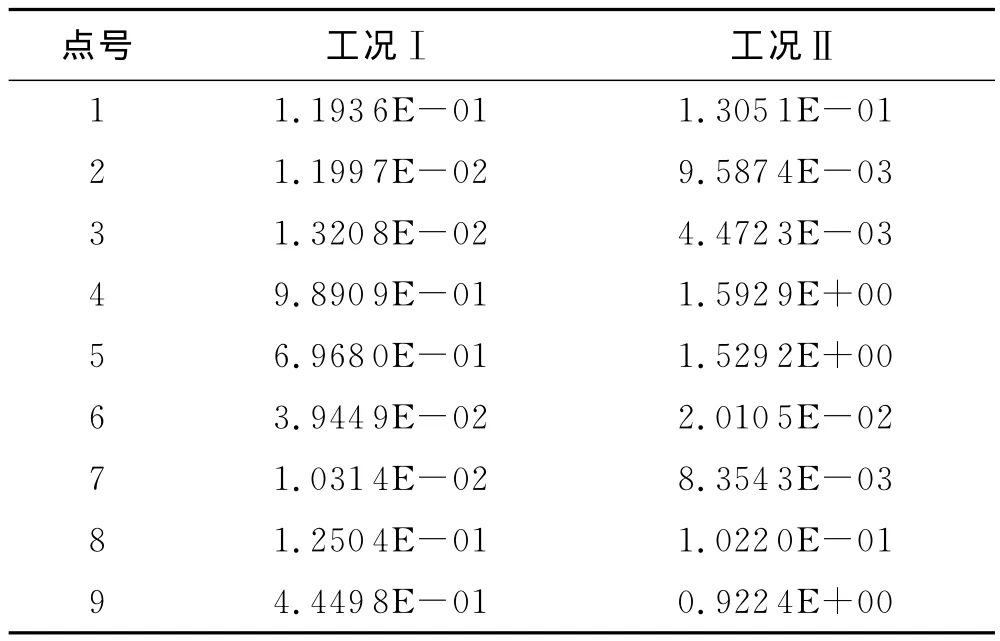
表3 A－A截面关键点应力值［4］（单位：MPa）

由于有限元模型在支点（边跨）截面处，边界约束采取了约束T梁底部线单元竖向、横向位移，在此位置出现应力集中，故在截面下缘出现超出混凝土抗拉强度的拉应力，这里不予考虑（中跨支点截面亦如此）.由应力云图可以看出，由于正弯矩钢束在支点截面锚固，截面上预应力钢束锚固点处（深蓝色区域）出现压应力集中现象，这与实际情况相符.从图9和表3可以看出应力最大点是在4、5、9号点，预应力损失导致主拉应力显著增加，分别为61.0%、119.4%、107.3%.而其他点处应力受预应力损失影响较小.其中预应力损失20%后4号点最大拉应力达到1.59 MPa，快要达到接近C50抗拉强度设计值1.83MPa，说明靠近翼缘板与腹板交接处受预应力损失影响较大，在超载等不利因素作用下该位置更加容易因为混凝土主拉应力过大产生裂缝.

4.2 边跨跨中截面应力计算结果

各工况下边跨跨中B－B截面应力云图及各关键点应力值如图10～12及表4所示.

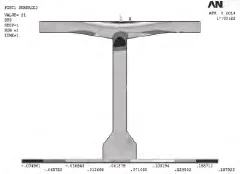
图10 工况Ⅰ，B－B截面应力云图

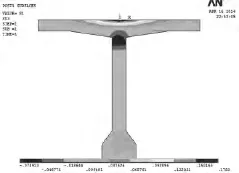
图11 工况V，B－B截面应力云图

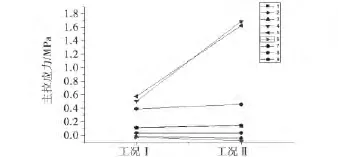
图12 B－B截面关键点应力变化趋势图

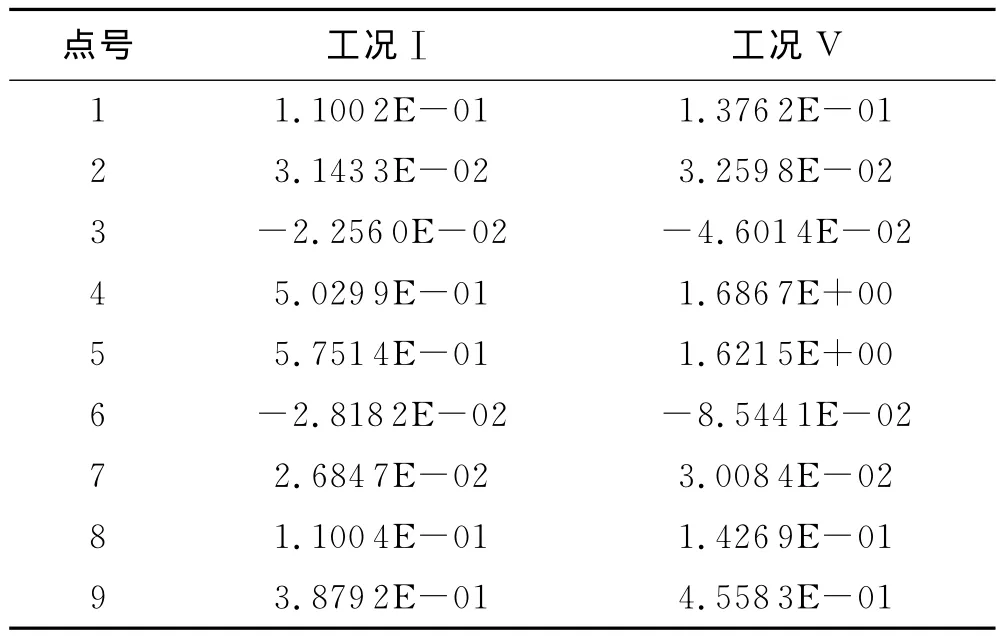
表4 B－B截面关键点应力值［4］（单位：MPa）

由图12和表4可以看出最大应力点在4、5号点，预应力损失20%的情况下，主拉应力增长明显，分别为235.3%、181.9%，最大主拉应力达到1.72 MPa，说明跨中截面靠近翼缘板与腹板交接处主拉应力较大，且受预应力损失影响较大，在其他不利因素作用下更容易产生裂缝.

4.3 中跨支点截面应力计算结果

各工况下中跨支点C－C截面应力云图及各关键点应力值如图13～15及表5所示.

图13 工况Ⅰ，C－C截面应力云图

图14 工况Ⅱ，C－C截面应力云图

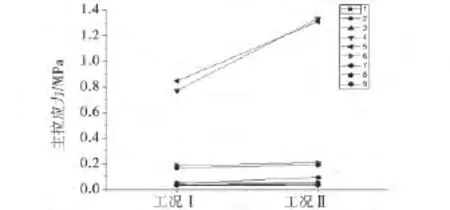
图15 C－C截面关键点应力变化趋势图

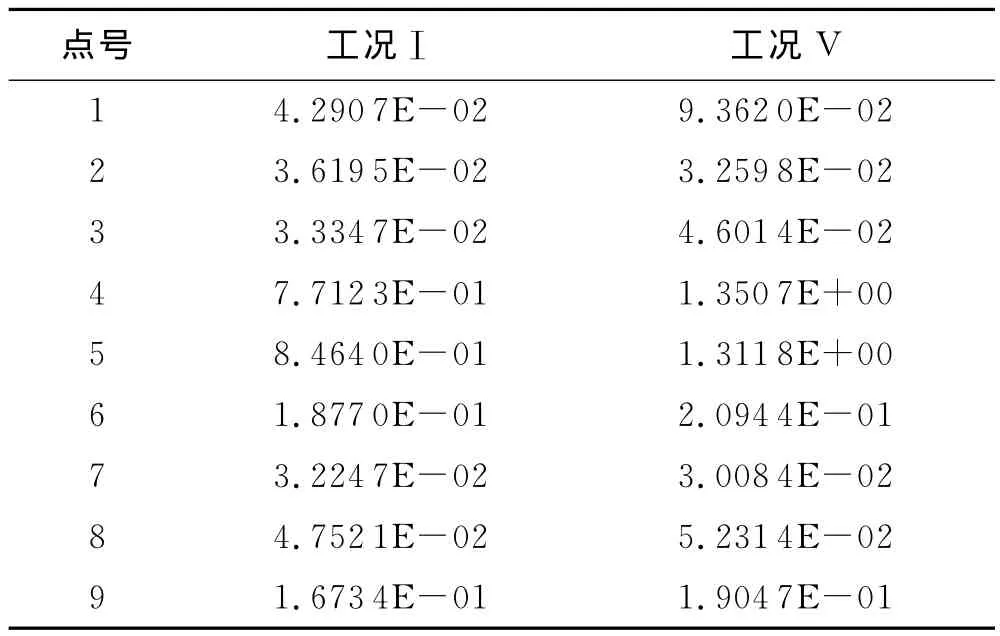
表5 C－C截面关键点应力值［4］（单位：MPa）

由图15和表5可看出，与边跨相同应力最大点也是在4号点和5号点，预应力损失20%时主拉应力的增大明显，最大主拉应力为1.35MPa分别为75.13%、54.9%，而其他点处应力变化幅度都非常小.说明靠近翼缘板与腹板交接处受预应力损失影响较大.

4.4 中跨跨中截面应力计算结果

各工况下中跨跨中D－D截面应力云图及各关键点应力值如图16～18及表6所示.

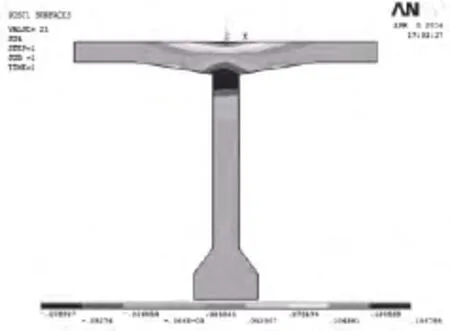
图16 工况Ⅰ，D－D截面应力云图

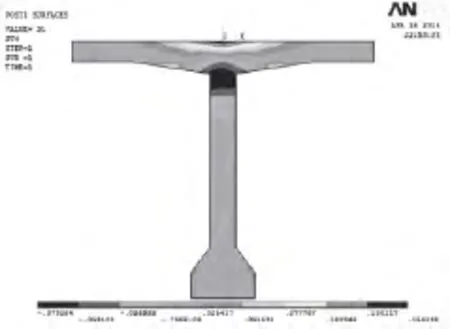
图17 工况Ⅱ，D－D截面应力云图

图18 各工况下D－D截面关键点应力变化趋势图

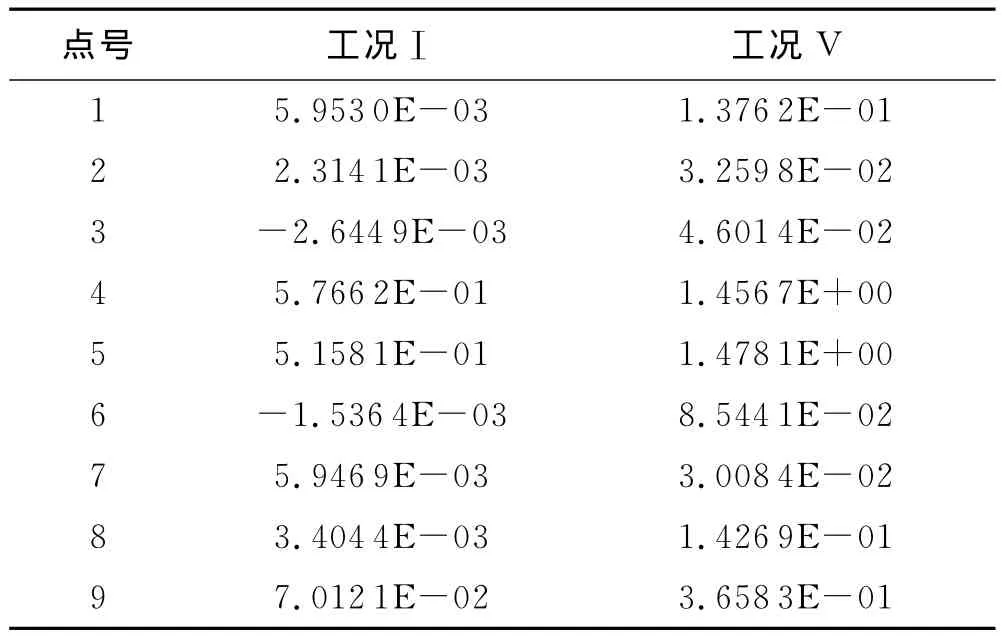
表6 D－D截面关键点应力值［4］（单位：MPa）

由图18和表6可知，4号点和5号点作为最大应力点，预应力损失20%后主拉应力增加幅度明显，分别为152.6%、186.6%，其他点处应力变化幅度比较小，说明翼缘板与腹板交接处受预应力损失影响程度较其他位置更大.

5 结 论

以福建某T梁桥为依托工程，考虑不同程度的预应力损失，比较分析不同的损失值对翼缘板截面上各关键点处的应力状态的影响，判断预应力损失对翼板不同位置的影响程度.

1）预应力损失主要对翼缘板上4、5号点处的应力增长贡献明显，其他点处的应力变化幅度相对较小，说明翼缘板与腹板交接附近应力受预应力损失影响较大，桥梁运营过程中在超载等不利因素共同作用下，更容易造成主拉应力过大，引起开裂.

2）边跨、中跨跨中截面主要应力点4、5号关键点在预应力损失20%时，主拉应力增加235.3%、181.9%和152.6%、186.6%，说明相对于支点截面跨中附近截面受预应力损失影响更加明显，荷载共同作用下，更容易引起跨中附近截面应力过大.

［1］ 范立础.预应力混凝土连续梁桥［M］.北京：人民交通出版社，1999.

［2］ 陈 强.先简支后连续结构体系研究［D］.浙江大学，2002.

［3］ 李 涛.简支后连续T型梁桥预应力监测试验研究［D］.重庆：重庆交通大学，2010.

［4］ 叶见署.结构设计原理［M］.北京：人民交通出版社，2010.

［5］ 龙佩恒，陈惟珍.应用空间嵌入式实体组合单元分析PC桥梁结构［J］.同济大学学报：自然科学版，2007，35（4）：455－460.

［6］ 王新敏.Ansys工程结构数值分析［M］.北京：人民交通出版社，2007.

［7］ 孙训方，方孝淑，关来泰.材料力学（I）［M］.北京：高等教育出版社，2002.