基于贝叶斯参数更新的高土石坝坝顶开裂风险动态评估与预警

黄会宝，熊敏，高志良，吴震宇，李俊儒，尹川

（1.四川大学水利水电学院，四川成都 610065；2.四川大学水力学及山区河流开发保护国家重点实验室，四川成都 610065；3.国能大渡河流域水电开发有限公司，四川成都 610041）

0 引言

土石坝对地形地质条件适应性强，可以充分利用当地材料，造价较低，是水电开发中最具应用前景的坝型之一［1，2］。在我国已建土石坝中，溃坝事故主要集中在中低高度大坝，高土石坝主要表现为坝顶开裂、坝体与坝肩（基）渗漏、坝坡滑坡塌坑等非溃坝故障模式，根据相关文献统计，坝顶开裂约占高心墙堆石坝常见故障模式的40%以上［3-5］。

众所周知，坝顶开裂与土石坝的变形特性密切相关，特别是变形倾度指标［6-8］。通过大坝原观监测数据，结合参数反演算法和数值模拟方法可以对高心墙堆石坝运行形态进行准确预测［9，10］。当基于数值模拟结果计算出的坝顶变形倾度大于某一阈值时，坝顶存在开裂可能性，但是并不意味着坝顶会立即开裂［11，12］，若坝顶变形倾度超过阈值的异常状态持续时间较长，坝顶开裂的可能性就会随着异常状态的持续时间而增大。由于复杂的物理机制和随机因素，坝顶开裂前的异常状态持续时间是不确定的，可以看作是一个随机变量，并可以基于此对异常状态期间发生坝顶开裂的风险进行评估。

由于缺乏相关的历史资料，特别是对于某一具体的土石坝，无法通过经典的频率统计分析得到坝顶开裂前异常状态持续时间的概率分布参数（PDP）。根据异常状态开始到发生峰值之间的观测时间间隔，可以利用贝叶斯理论估计PDP 的概率分布［13］。此外，PDP 的概率分布可以随着观察到的证据的积累过程而动态更新。因此，在贝叶斯框架下，土石坝的坝顶开裂风险可以根据PDP 的逐步更新概率分布进行动态评估。此外，还可以根据概率估计的开裂时间范围对坝顶开裂进行预警。

本文研究的主要问题是：①如何用坝顶沉降异常状态持续时间来评价土石坝坝顶开裂风险；②如何估计给定概率区间对应的坝顶开裂次数以进行坝顶开裂预警；③如何更新坝顶开裂风险公式中参数λ的概率分布。

1 坝顶开裂风险动态评估与预警方法

1.1 总体思路与方法架构

首先确定高心墙堆石坝坝顶异常状态判定准则。如引言所述，坝顶开裂与坝顶变形倾度γS密切相关。当γS超过某一阈值时，坝顶易发生开裂故障。变形倾度的定义是［14］：

式中：γS为变形倾度；ΔS为同一高程上两点的沉降差；ΔL为两点之间的水平距离。

采用数值模拟计算坝顶裂缝两侧变形倾度，为使计算结果可以准确描述坝体变形，基于大坝原观变形监测数据对数值模型的材料参数进行反演分析。坝顶开裂前的异常变形状态定义为γS＞γC，γC为异常变形的阈值（即临界倾度）。有学者根据土梁挠曲试验，提出γC的取值范围为0.5%～0.65%［15］；或根据部分土石坝开裂前变形倾度的统计数据，提出γC可采用0.6%［16］、0.7%［17］或1%［18］等值。从偏保守角度考虑，本文取γC=0.5%。

坝顶开裂前异常状态的持续时间TAS是不确定的，因此本文将TAS视为随机变量，并假定TAS服从指数分布，故而坝顶开裂的概率可以表示为异常状态持续时间TAS的函数。一旦出现异常状态（如γS＞γC），就可以用TAS来估计坝顶开裂的概率。此外，还可以推导出与给定的开裂概率相对应的开裂时间。由于不具备与坝顶开裂概率相对应的先验知识，因此通过对观察到的开裂次数的计算概率的统计分析来选择和更新估算开裂时间的概率。

坝顶开裂概率计算中的参数是不确定的。如何估计参数的概率分布是该方法应用中的一个主要问题。应用贝叶斯理论，根据观测到的从出现异常状态到出现坝顶开裂的时间间隔，估计和更新参数的概率分布。

上述方法的总体流程如图1所示。

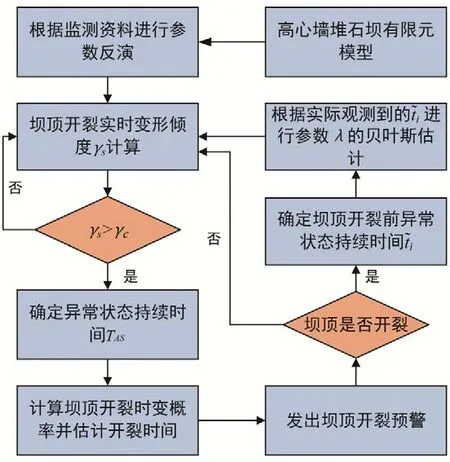
图1 坝顶开裂动态风险评价与预警流程图Fig.1 Flowchart of the dynamic risk evaluation and early warning of crest cracking

1.2 坝顶开裂概率与预警

如前所述，坝顶开裂前异常状态的持续时间TAS是不确定的，其不确定性可以用概率密度函数（PDF）定量描述。指数分布可以用来描述服从泊松分布的独立随机事件的时间间隔的概率分布［19］。因此，采用指数分布来表示坝顶开裂前异常状态持续时间TAS的概率分布，其PDF如下：

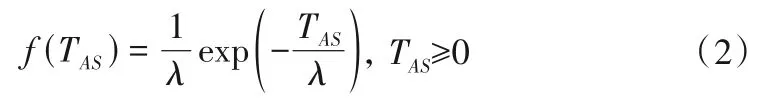
式中：λ是TAS的概率密度函数参数，λ=E（TAS），即λ是坝顶开裂前异常状态持续时间的期望值。

当坝顶沉降的异常状态（即γS＞γC）发生并持续时，在给定的时间内出现坝顶开裂的概率为：

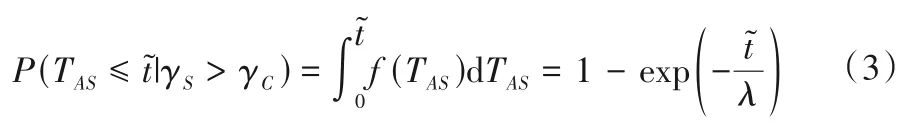
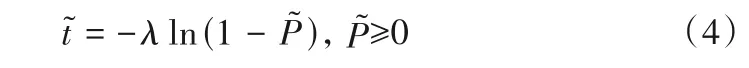
从公式（3）中可以看出，坝顶开裂风险评估的合理性与准确性取决于参数λ的取值。由于缺乏高心墙坝坝顶开裂前异常状态持续时间的历史数据，使得参数λ值存在很大的认识不确定性，特别是对于具体的大坝而言。在坝顶开裂风险评估中，应考虑到这种认识不确定性的影响。在贝叶斯框架下，认知不确定性可以用主观概率来量化，本研究应用贝叶斯理论，根据观测到的坝顶开裂前的异常状态持续时间，对λ的主观概率分布进行估计和更新。

1.3 信息驱动的风险模型参数更新

参数λ中的认知不确定性源于分析人员对λ的统计信息的缺乏。这种认知不确定性可以用贝叶斯框架中的主观概率定量地表示。当获得与参数λ有关的信息时，可以根据贝叶斯定理估计和更新λ的概率分布如下：

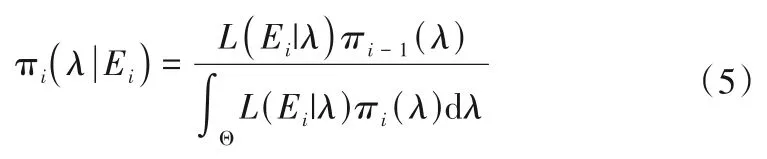
式中：πi(λ|Ei)是在获得第i个信息的情况下λ的后验概率分布；πi-1(λ)是λ在获得第i个信息之前的先验概率分布；L(Ei|λ)是似然函数（即给定λ值下观测信息的条件概率）；Θ 是λ的定义域。

如何建立似然函数是用公式（5）更新λ概率分布的关键步骤，在土石坝的长期运行过程中，可以观察到与λ估算直接相关的两类信息。根据这两类信息，似然函数可构造如下：

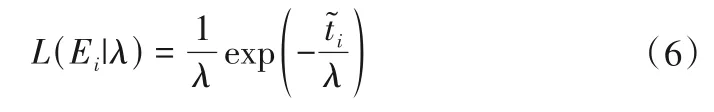
（2）第二类信息：从异常状态出现到异常状态结束，未出现坝顶开裂的持续时间，相应的似然函数表述为：

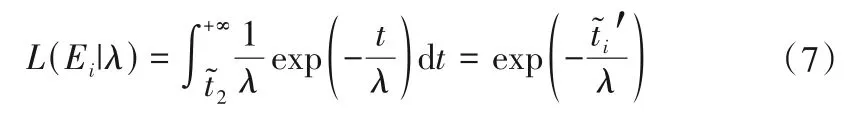
根据新观测信息的类型，将相应的似然函数和λ的先验概率分布代入公式（5），即可更新λ的概率分布。当第一次估计λ的概率分布时，没有任何关于λ的先验信息，此时采用均匀分布来表示π0(λ)：

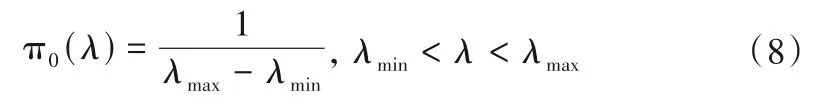
式中：λmin和λmax分别是λ的可能最小值和最大值。

从λ的后验概率分布中抽样，将λ的样本代入公式（3）和（4），可以计算出坝顶开裂概率和开裂时间的均值和置信区间。

2 工程案例

2.1 工程概况

某心墙堆石坝最大坝高为186 m，坝顶宽度为14 m，主要防渗结构为砾石土心墙及坝基防渗墙，心墙上、下游侧与坝壳堆石间设反滤层及过渡层，其典型横剖面见图2，其中内部水平变形测点（CH17～CH31）与沉降位移测点（SG17～SG31）同点布置。

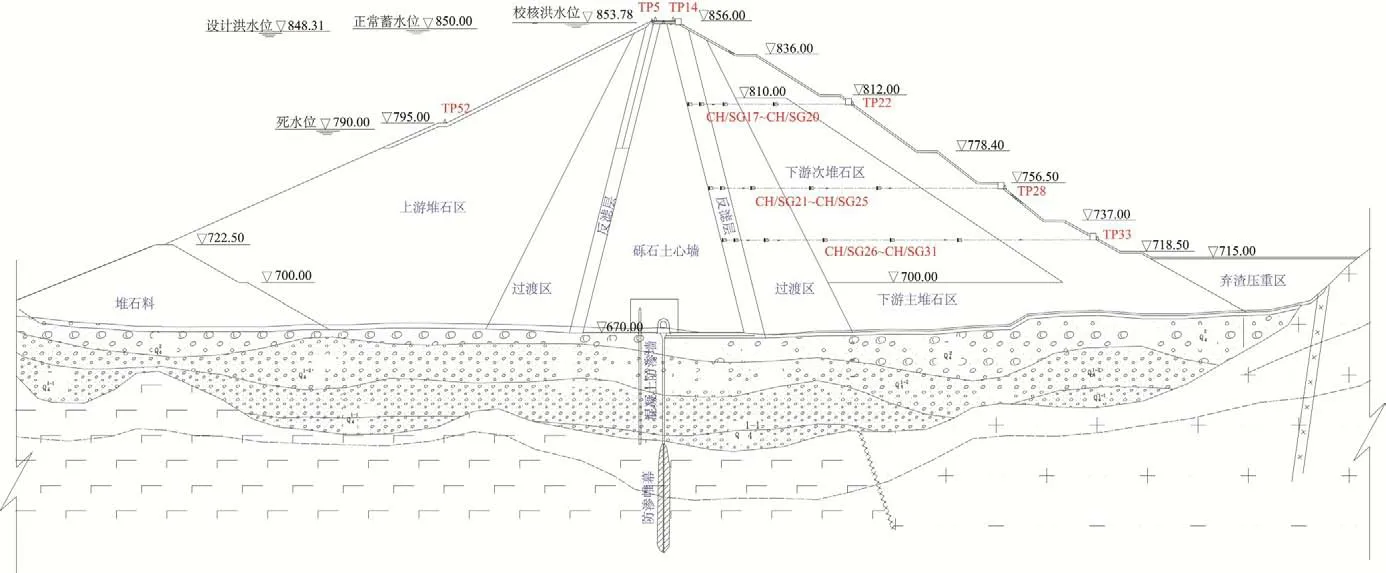
图2 某心墙堆石坝典型横剖面（单位：m）Fig.2 Typical cross section of the core rockfill dam

大坝始建于2004 年3月，2009 年9 月竣工，该水库的第一次蓄水始于2009 年11月，水库水位于2010 年11 月上升到正常水位（850.00 m），此后水库水位在死水位（790.00 m）和正常水位之间周期性波动。大坝填筑过程和库水位变化过程如图3所示。

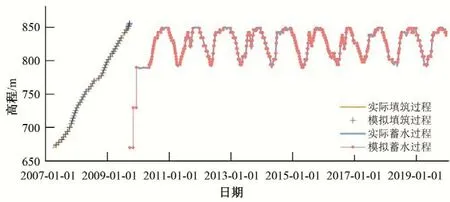
图3 大坝填筑过程及库水位变化过程Fig.3 Dam filling process and fluctuation of reservoir water level

2.2 大坝坝顶开裂情况

该大坝在首次达到正常蓄水位后，于2010 年12 月21 日首次在坝顶坝轴线位置发现纵向裂缝，采用沥青封堵进行处理，此后历年高水位运行期间均出现坝顶开裂现象。坝顶首次发生裂缝后进行了挖探坑检查，查明裂缝深度约为1.5～2 m，长度约230 m。由于坝顶与砾石土心墙顶部的垂直距离为2 m，因此裂缝未延伸至砾石土心墙，此外，心墙渗压监测数据也没有出现异常。虽然坝顶裂缝并没有直接危害砾石土心墙的安全，但由于降雨入渗可能侵蚀大坝内部材料，需要对裂缝及时进行封堵，因此，在大坝运行过程中有必要对坝顶开裂风险进行评估和预警，提前做好坝顶开裂后的修复准备。

3 案例分析结果

3.1 坝顶时序变形倾度及异常状态识别

采用本文提出的方法对多次观测到坝顶开裂的大坝典型横剖面进行分析，图4 为该剖面的有限元模型。采用邓肯-张E-B 模型计算大坝瞬时变形，采用七参数模型计算大坝蠕变变形［20］，采用三参数模型计算大坝首次蓄水产生的湿化变形［21］。实测水平及沉降位移与计算值对比如图5所示。

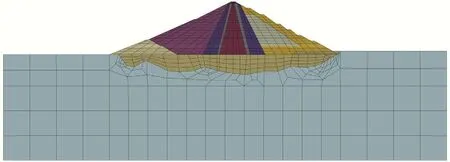
图4 大坝典型横剖面的有限元模型Fig.4 Finite element model of typical cross section of the dam

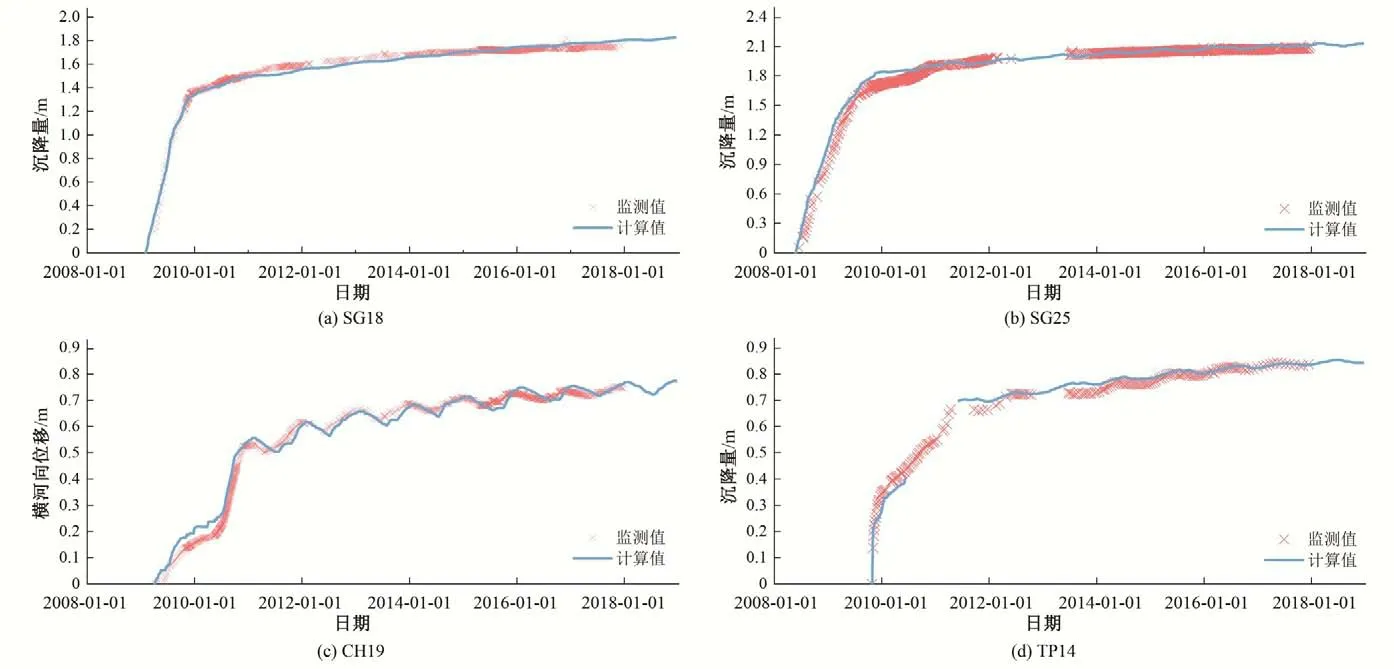
图5 实测水平及沉降位移与计算值的对比Fig.5 Comparison of the computed and measured horizontal and settlement displacements

在本研究中坝顶裂缝处变形倾度是通过有限元计算裂缝两侧节点沉降位移后代入式（1）得到的，为保证坝顶变形梯度的计算精度，基于SG18、SG25、CH19和TP14四个测点的监测数据进行参数反演，采用响应面法代替耗时的有限元计算［22］，采用粒子群优化算法进行目标函数寻优［23］。图5为各测点水平及沉降位移的实测值和反演计算值的对比，可以看出两者的变化规律一致，量值接近，运行期和实测水平及沉降位移与计算值的相对误差在6%以内，表明本文数值模型可以比较准确地预测大坝运行过程中的变形状态。

计算得到的坝顶顺河向沉降变形倾度过程线如图6 所示，图6 中还标出了历次坝顶开裂时间。由图6 可见，坝顶顺河向沉降变形倾度与库水位具有明显正相关关系，库水位上升时变形倾度相应增大，最大变形倾度为0.98%。由图6 可见，坝顶开裂都发生在变形倾度较大时，此外，坝顶出现异常变形状态到坝顶开裂之间的时间间隔具有明显的随机性。

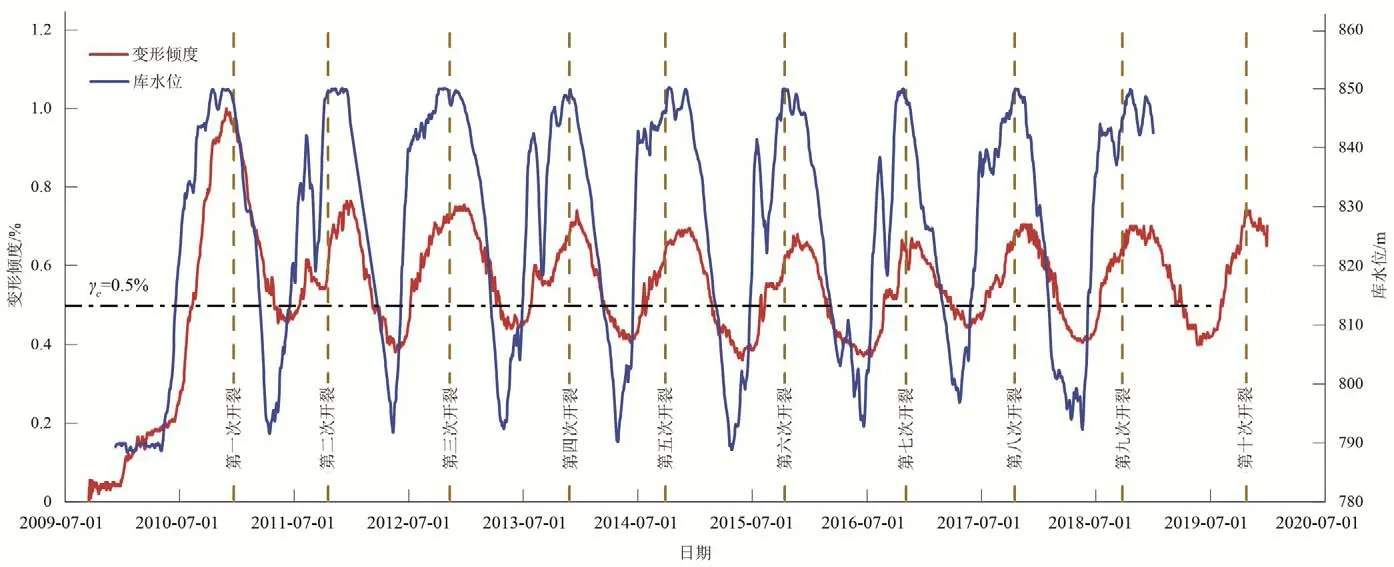
图6 坝顶变形倾度过程线及开裂时刻Fig.6 The time series of crest settlement inclination and the cracking time

3.2 开裂风险模型参数λ概率分布的贝叶斯估计

由于坝顶开裂前的异常状态持续时间TAS是不确定的，本文假定其为服从指数分布的随机变量。由于其参数λ也是不确定的，因此，根据TAS的观测值，应用2.3 节所述的贝叶斯方法估计λ的概率分布。对于第一次坝顶开裂，λ的先验分布为均匀分布，其中λmin和λmax分别取0 d 和300 d。图7 为历次坝顶开裂后λ的后验分布概率密度曲线，表1给出了λ的统计特征值。

由图7 可见，在有限的观测信息下，λ在第一、第二、第三和第四次坝顶破裂后的后验分布具有明显的重尾特征。随着信息（即坝顶开裂前的异常状态持续时间）的积累，λ的概率分布的离散程度逐渐减小。从表1也可以看出，随着观察到的TAS的增加，λ的标准差从72 d 下降到41.4 d。因此，观察信息的增加可以显著降低λ的不确定性，这与统计学原理是一致的。

表1 参数λ的统计特征值Tab.1 Statistical characteristics of λ

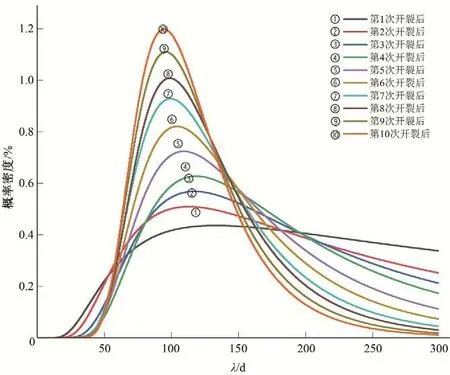
图7 参数λ概率分布的动态更新结果Fig.7 Progressively updated distributions of λ

3.3 坝顶开裂风险的动态评估和预测预警

为了对坝顶开裂风险进行动态评估，基于更新后的λ的概率分布，根据式（3），采用蒙特卡罗法对坝顶时变开裂概率进行计算。图8给出了历次坝顶开裂的时变风险概率的均值、5%和95%分位值，以及观察到的实际开裂时间和相应的开裂概率均值，其中时间轴的原点对应坝顶开裂前变形异常状态的开始时刻。由图8 可见，开裂概率随异常变形状态持续时间的延长而增大。随着观测数据的积累，由于λ的不确定性逐渐减小，开裂概率估计值的置信区间逐渐缩小，开裂风险评估的不确定性降低。值得注意的是，与实际开裂时间对应的开裂概率的均值不是一个确定值。

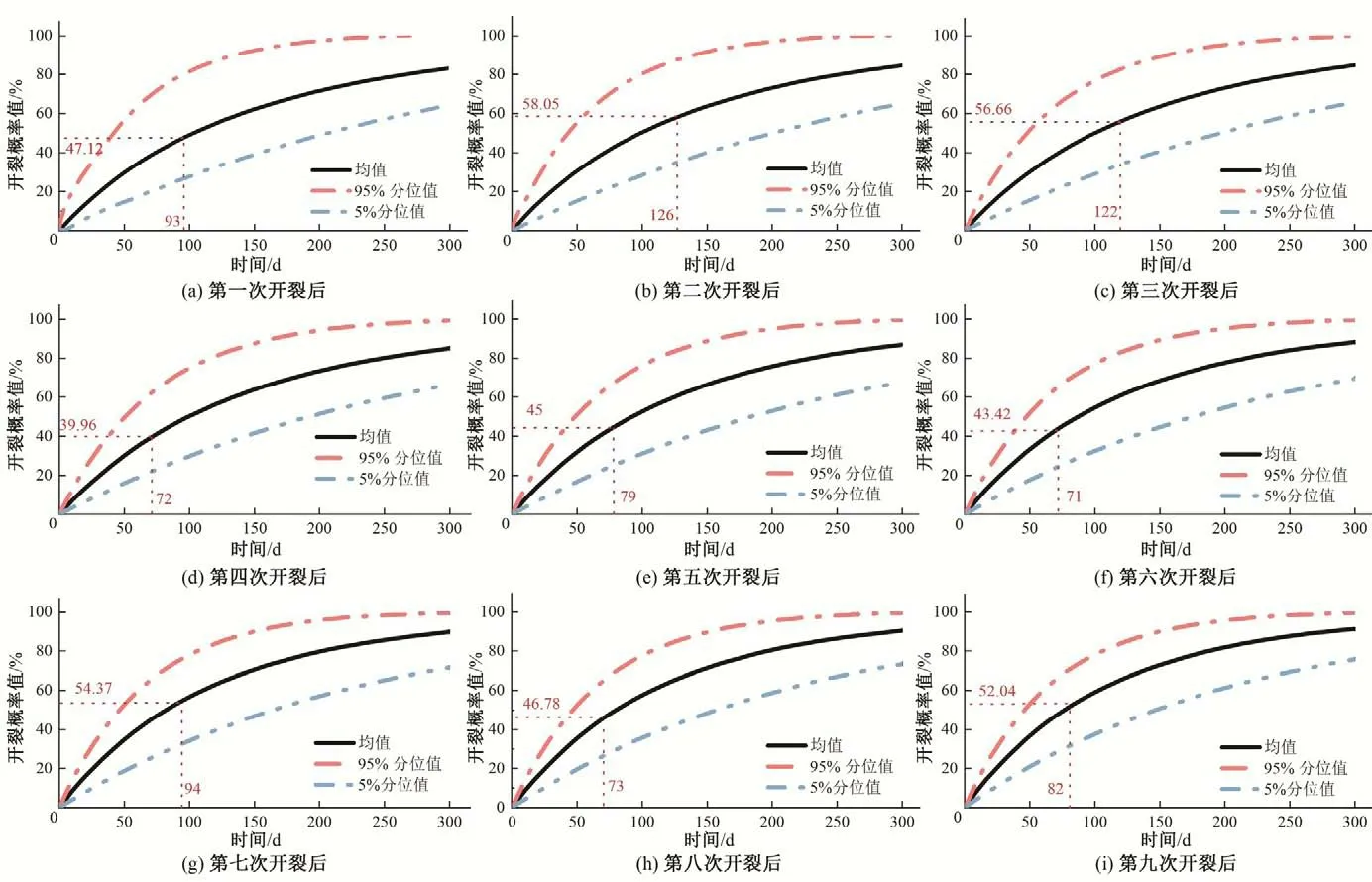
图8 坝顶历次开裂前估计的开裂时变概率Fig.8 Estimated time-varying cracking probability

在给定开裂概率的情况下，可以利用公式（4）估计坝顶开裂时间。因此，开裂时间的预测精度取决于预警所采用的开裂概率阈值。由于与实际开裂时间对应的开裂概率具有随机性，因此，根据λ的概率分布，计算开裂概率阈值的均值和置信区间。计算结果表明，坝顶开裂时刻对应的开裂概率的均值约为50%，5%和95%分位值分别约为25%和80%。

根据开裂概率阈值的均值和5%、95%分位值，结合逐步更新的λ均值（见表1），采用公式（4）预测坝顶开裂时间。开裂时间预测值的均值、上限和下限如图9所示，并与实际开裂时间进行了比较。结果表明，坝顶实际开裂时间介于预测开裂时间的上限和下限之间，与开裂时间预测值的均值较为接近。利用预测的开裂时间的下限进行坝顶开裂预警，可以看出，在坝顶发生开裂前20～70 d（即实际开裂时间与预测的开裂时间之间的间隔）可发出预警。因此，大坝安全管理单位可以根据坝顶开裂的早期预警，提前做好裂缝修复的准备工作。

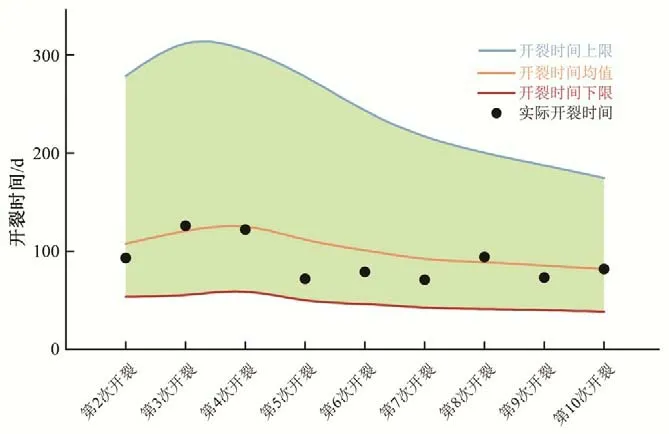
图9 坝顶开裂时间的预测Fig.9 Prediction of dam crest cracking time

4 结论

本文针对传统大坝安全风险评估方法存在定量化不足，不能实时跟踪大坝安全风险的动态变化，可能会错过故障发现及解决的最佳时间等问题，提出了集时变风险分析和参数动态辨识于一体的高土石坝坝顶开裂风险动态评估与预警方法，实现了坝顶开裂时变概率的动态分析和基于概率的坝顶开裂风险提前预警，为高土石坝坝顶开裂风险预测预警和主动调控提供了科学依据。

通过对某高心墙堆石坝坝顶开裂的风险评估和预警，对该方法进行了验证。结果表明，随着观察到的坝顶开裂信息的积累，风险模型参数λ后验分布的离散程度逐渐减小。坝顶开裂概率随异常变形状态持续时间的延长而增大，开裂概率估计值的置信区间随λ分布的更新而逐渐缩小。通过对坝顶开裂时间下限的预测，可以在坝顶开裂发生前至少20 天发出预警，有利于大坝管理单位提前做好裂缝修复的准备工作，提高大坝安全保障水平。