基于坝基散射波衰减影响的重力坝动力响应分析
2015-07-25刘依松陈灯红
刘依松 陈灯红
(1.三峡大学 水利与环境学院,湖北 宜昌 443002;2.三峡大学 土木与建筑学院,湖北 宜昌 443002)
系统评价重力坝抗震安全性的关键之一是解决大坝与地基的动力相互作用的问题.Clough对此提出了一种无质量地基模型,认为大坝附近一定范围的地基是线弹性、无质量的、地震激励均匀作用于截断边界上.这种模型虽在工程中应用较广,但存在局限性:①地基实际上是有质量的半无限介质,地震波动能量向无限远处散逸,即无限地基的幅射对散射地震波动能量将起到一种吸能作用;②深山峡谷中的高坝,其基底延伸较长,沿坝基交界面的地震动振幅和相位差异明显,高坝空间整体作用效应明显,忽略这种不均匀性将难以反映坝体的实际地震反应.为了克服这些不足,近年来,Lysmer等[1]提出了黏性边界,Deeks等[2]提出了时域解耦的黏弹性边界,廖振鹏等[3]提出了透射边界等,比例边界有限元法[4-5]也在发展之中.但黏性边界仅考虑边界吸能阻尼,未计入介质弹性恢复影响,易致低频漂移.透射边界常会高频失稳,需增设许多边界节点和单元.黏弹性人工边界条件基于衰减散射波的影响,在人工边界上设置并联弹簧和阻尼器,使得低频精度好,高频稳定性好.采用基于衰减散射波的黏弹性思想,建立了重力坝-地基系统[6]二维平面黏弹性模型,采用ANSYS中的APDL参数化设计语言进行重力坝动力响应分析.
1 研究方法
1.1 黏弹性人工边界
将波阵面方程引入几何扩散因子,Deeks[2]、刘晶波[7-9]推衍出反映无限介质弹性恢复性能的黏弹性人工边界条件.将平面波和远场散射波混合经验叠加且考虑多角度透射,杜修力[10-11]改进了黏弹性边界公式,对于波源问题、衰减散射波问题均有较好的计算精度.对于二维黏弹性边界,刚度系数和阻尼系数为

式中,KBN、KBT分别表示法向和切向弹簧系数,rb为散射波源至人工边界的距离,λ为拉梅常数,G为介质剪切模量,ρ为介质质量密度,并具有G=和λ+2G=的关系;CBN、CBT分别为表示法向和切向阻尼系数,cp、cs分别为P波和S波波速,α、β为无量纲参数,分别取0.8、1.1.
黏弹性人工边界作为一种应力连续分布的人工边界条件,可采用与普通单元类似的形函数进行离散,结点i处的形函数为

位移形函数矩阵为
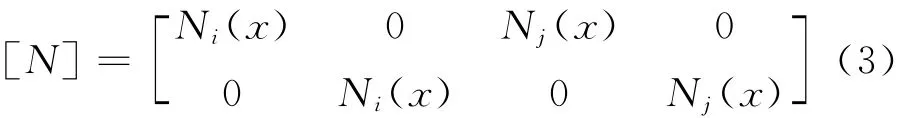
黏弹性人工边界上分布的弹性矩阵为
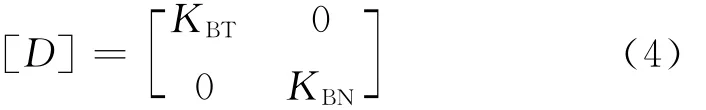
单元的刚度矩阵公式为

经式(5)计算得到,黏弹性人工边界单元的刚度矩阵如式(6),阻尼矩阵具有相同的形式,只需将刚度系数K用相应的阻尼系数C替换即可.

其中,l为黏弹性人工边界单元的长度.
1.2 地震荷载输入方法
黏弹性边界能够吸收由近场向远域散射的外行波,将外源地震波引入计算区域时,只需在人工边界处施加自由场荷载即可,可以把近域地基作为半无限空间自由场地基的子结构,由其在入射地震波作用下的边界相互作用力给出[10-11]


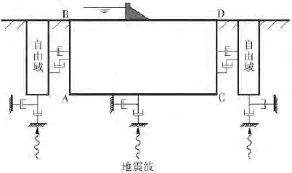
图1 坝-地基系统黏弹性边界及自由场示意图
自由场应力可由弹性理论求得,即
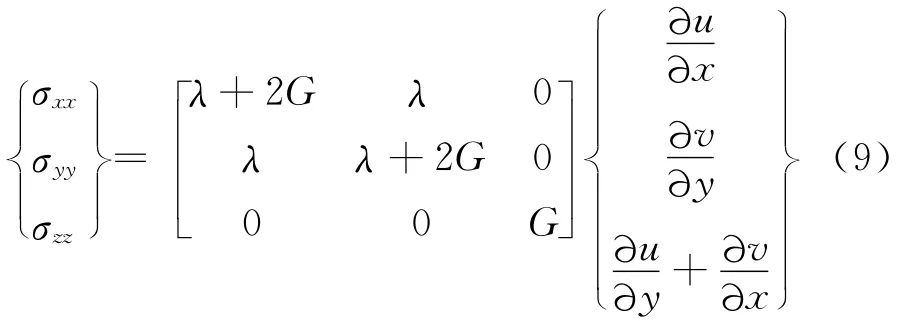
当在底边界垂直入射P波时,底部的边界条件为u=0,v=v0(t),则自由场在沿高度h处,自由场位移、速度可表示为入射波和反射波的叠加,即

式中,H为底边界到自由表面的距离.
并且对于底部边界,有h=0,n=[0-1]T,则将式(10)代入式(9)中,可得自由场应力σfb为
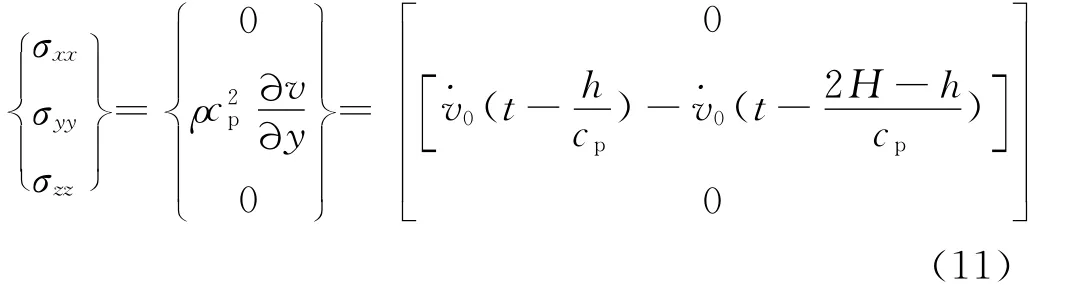
将式(10)、(11)代入式(8)中,等效荷载FB可求得,即

当在底边界垂直入射SV波时,底部的边界条件为u=u0(t),v=0,按照同样的方法,等效荷载FB为

对于侧边界的自由场应力也可按类似的方法推导出.
2 数值实现与算例验证
黏弹性人工边界具有较多优点,最主要的是和有限元的结合实现起来比较方便,只需在有限元模型人工边界上结点的法向和切向分别设置并联的弹簧单元和阻尼器单元.在ANSYS程序中,弹簧-阻尼器元件可以用COMBIN14单元来模拟,该单元具有弹簧和阻尼选项.值得一提的是,在实际的有限元实现过程中,各向边界物理元件参数的实际取值等于式(1)给出的量值与对应有限元结点所代表网格面积的乘积.利用ANSYS中的APDL参数化设计语言,编写了实现黏弹性人工边界的宏文件VSB.mac,程序流程图如图3所示.利用Fortran语言编写了式(12)、(13)所示的加载子程序Load.for,可以方便地施加等效地震荷载.

图2 弹性半空间网格图
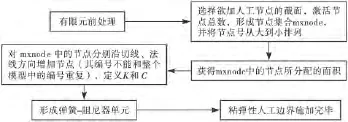
图3 黏弹性人工边界程序流程图
为验证上述黏弹性边界单元及波动输入方法程序的正确性,现采用均匀弹性半空间[12]受底部垂直入射SV波进行验证.波动输入采用的力学计算模型如图2所示.介质的力学参数为:弹性模量E=13.23 GPa,泊松比ν=0.25,质量密度ρ=2 700kg/m3,波速为cs=1 400m/s,cp=2 425m/s,计算区的范围为762m×381m,有限元单元尺寸为19.05m×19.05 m,时间步长取为0.01s,入射波的方程见式(14).

经过计算得到 A(-381,381),B(0,381),C(381,381),D(381,0),E(0,0)等5个点的x向位移时程,如图4所示.
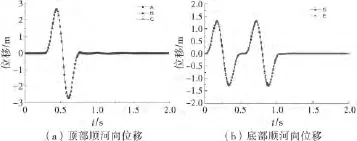
图4 顶部和底部位移时程
从A、B、C 3个点的x向位移时程图可以看出:A、B、C 3点的位移值相同,说明是由入射波和反射波共同引起的位移时程,且顶部的最大值为接近SV入射波幅值的2倍.从D、E两个点的位移时程图可以看出,D、E两点位移值相同,位移曲线的前半段为入射波引起的位移时程,后半段为反射波引起的位移时程.5个点的解均与理论解相吻合.因此,在ANSYS编写的黏弹性边界单元及实现波动输入子程序是正确的.
3 工程应用
某水电站具有发电、防洪、航运等综合效益,属Ⅰ等大(1)型工程,大坝为碾压混凝土重力坝,与泄水建筑物同为1级建筑物,防洪标准按500年一遇设计,10 000年一遇校核.7孔溢流坝布置于河床中央,溢流坝段右侧为挡水坝段,坝段宽22m,坝顶宽18m,下游坝坡1∶0.73.上游坝坡在高程270.00m以上为直立坡、以下为1∶0.25的斜坡,坝体横剖面见图5所示.坝址的地震基本烈度为7度,大坝按8度地震控制,设计烈度为8度,设计地震加速度为0.2g.按照本文分析方法,结合波动输入子程序,在正常蓄水位条件下,对大坝-地基系统进行考虑地基辐射阻尼效应的抗震分析,有限元网格如图6所示.

图5 坝体位移和应力的关键部位

图6 坝体网格图
在计算过程中,地震荷载不再按照惯性力输入,而是将合成的人工地震波及反应谱(见图7)加速度转化为位移、速度,然后求得自由场应力,进行等效地震荷载输入.输入的各向位移、速度如图8所示.动力时程分析各特征点的位移、应力结果见表1,不同地震输入模型下坝体位移时程比较如图9所示,坝体关键部位的应力比较如图10所示.

图7 合成的人工地震波及反应谱
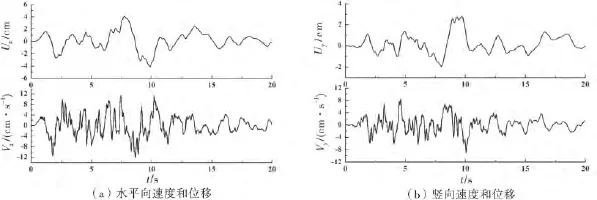
图8 输入的各向速度和位移
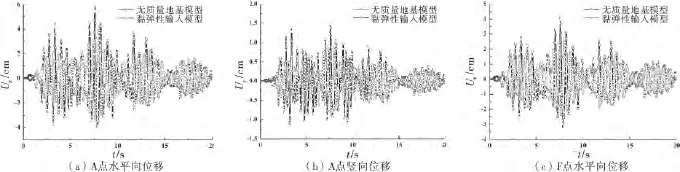
图9 不同地震输入模型位移值比较

图10 不同地震输入模型应力值比较
由表1可知,考虑了黏弹性人工边界后的无限域地基辐射阻尼影响的地震响应分析所得到的大坝-地基动力响应峰值比固定边界无质量地基模型的所得结果减小了4%~38%.

表1 特征点位移、应力峰值比较
4 结 论
1)在有限元模型人工边界上结点的法向和切向分别设置一系列并联的弹簧和阻尼器单元,以考虑基于衰减散射波的地基辐射阻尼的影响,利用ANSYS中的APDL参数化设计语言,编写实现黏弹性人工边界的宏文件,对重力坝-地基系统进行了动力响应分析.
2)与无质量地基模型相比,考虑了黏弹性人工边界后的无限域地基辐射阻尼影响的地震响应分析的大坝-地基动力响应峰值降低了4%~38%.
3)无质量地基模型并非是有限的、线弹性的、无质量的均匀作用于截断边界上,而是夸大了结构的动力响应,所得成果偏于保守,需要改进和优化.在进行动力响应分析时,考虑无限域地基的辐射阻尼影响更符合工程实际.
[1] Lysmer J,Kuhlemeyer R L.Finite Dynamic Model for Infinite Media[J].Journal of Engineering Mechanics,ASCE,1969,95(1):759-877.
[2] Deeks A J,Randolph M F.Axisymmetric Time-domain Transmitting Boundaries[J].Journal of Engineering Mechanics Division,ASCE,1994,120(1):25-42.
[3] Liao Z P,Wong H L,Yang B.A Transmitting Boundary for Transient Wave Analyses[J].Scientia Sincia Methematica,1984,27:1063-1076.
[4] Wolf J P,Song Ch.The Scaled Boundary Finite-element Method-aprimer: Derivations[J].Computers and Structures,2000,78:191-210.
[5] Song Ch,Wolf J P.The Scaled Boundary Finite-element Method-aprimer:Solution Procedures[J].Computers and Structures,2000,78:211-225.
[6] 郝明辉,张艳红,陈厚群.基于ABAQUS的黏弹性人工边界在重力坝分析中的应用[J].中国水利水电科学研究院学报,2012,10(2):120-126.
[7] 刘晶波,谷 音,杜义欣.一致黏弹性人工边界及黏弹性边界单元[J].岩土工程学报,2006,28(9):1070-1075.
[8] Liu J B,Du Y X,Du X L.3DViscous-spring Artificial Boundary in Time Domain[J].Earthquake Engineering and Engineering Vibration,2006,5(1):93-102.
[9] 谷 音,刘晶波,杜义欣.三维一致黏弹性人工边界及等效黏弹性边界单元[J].工程力学,2007,24(12):31-37.
[10]杜修力,赵密,王进廷.近场波动模拟的人工应力边界条件[J].力学学报,2006,38(1):49-56.
[11]赵建锋,杜修力,韩 强,等.外源波动问题数值模拟的一种实现方式[J].工程力学,2007,24(4):52-58.
[12]贺向丽.高混凝土坝抗震分析中远域能量逸散时域模拟方法研究[D].南京:河海大学,2006.
