探析二次方程根的分布问题高考命题视角

☉江苏省丹阳高级中学 谢洪涛

教材是数学教育专家集体智慧的结晶，里面包含要求高中学生必须掌握的知识点及相关问题的解题思想方法，但受承载容量的限制，题型、方法的介绍不可能面面俱到，有一部分重要的题型和方法是以习题的形式体现的，因此对习题的拓展、探究就格外重要了.对习题的探究不仅可以对题型和方法进行归纳总结，而且还可以找到很多高考题的生长点.本文以一道二次方程根的分布的习题为例，就相关题型及解法进行探究.以期抛砖引玉.

题目（人教版必修5练习题）关于x的方程x2－（m+3）·x+m+3=0有两个不相等的正实数根，求实数m的取值集合.

教材中并没有对二次方程根的分布问题作系统的归纳，本文以此题为例，进行题型归纳及解题方法总结.

一、解法展示

解决此类问题可以从两种视角入手.

解法1：（利用二次函数图像）方程x2－（m+3）x+m+3=0有两个不相等的正实数根，即二次函数f（x）=x2－（m+3）x+m+3与x轴正半轴有两个不同交点.由二次项系数大于0知，二次函数f（x）的图像开口向上，欲使其与x轴正半轴有两个不同交点，则：

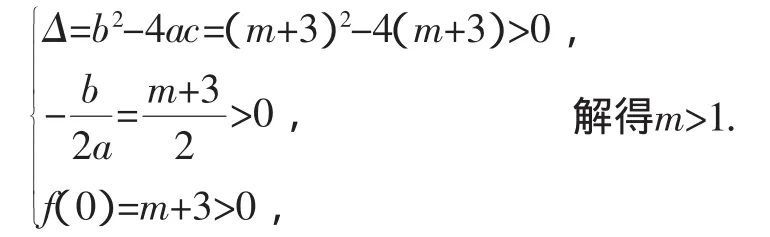
解法2：（利用根与系数的关系）方程x2－（m+3）x+m+3=0有两个不相等的正实数根，即：

解题中根据不同的题型，两种方法要择优而用.

二、题型归纳

设一元二次方程ax2+bx+c=0（a＞0）的两个实根为x1，x2，其根的分布问题除题目所示类型外，还有如下几种类型.

说明：在上述问题的解答中，若二次项系数的正负不确定，应就其可能取值情况进行分类讨论.若二次项系数可能为0，则问题转化为一次函数.

例1 若二次方程x2+（2m－3）x+4=0有且只有一个根在（0，1）内，求m的取值范围.

解析：令f（x）=x2+（2m－3）x+4，由f（x）=0有且只有一个根在（0，1）内可知，

①f（0）f（1）＜0⇒4（2m+2）＜0⇒m＜－1；

综上，m＜－1.

例2 若关于x的方程x2－x－m－1=0在［－1，1］上有两个根，求m的取值范围.

解析：令f（x）=x2－x－m－1，原问题转化为以下两种情况.

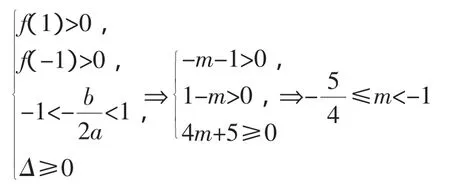
②f（1）f（－1）=0⇒m=±1.

当m=1时，原方程为x2－x－2=0⇒x1=－1，x2=2，不合题意；

当m=－1时，原方程为x2－x=0⇒x1=1，x2=0，合题意.

评析：在对上述两题的解答中，除了注意零点个数的不同，还需要注意所给区间端点的变化对问题的影响.

三、高考命题视角

高考中对二次方程根的分布问题的考查多数都体现在利用导数求解函数的综合题目中.解此类问题的基本策略是对函数求导后，在定义域内讨论导数的正负，而导函数多为二次型或局部为二次型，进而将问题转化为二次方程根的分布问题.

例3 （2015年山东理科）设函数f（x）=ln（x+1）+a（x2－x），其中a∈R.

（1）讨论函数f（x）极值点的个数，并说明理由；

（2）若∀x＞0，f（x）≥0成立，求a的取值范围.

解析：（1）f（x）=ln（x+1）+a（x2－x），定义域为（－1，+∞）.

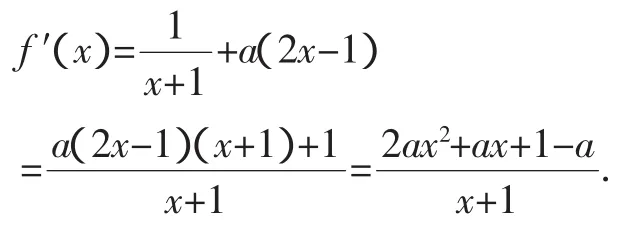
设g（x）=2ax2+ax+1－a，

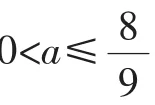
所以当x∈（－1，x1）时，g（x）＞0，f′（x）＞0，f（x）单调递增；当x∈（x1，x2）时，g（x）＜0，f′（x）＜0，f（x）单调递减；当x∈（x2，+∞）时，g（x）＞0，f′（x）＞0，f（x）单调递增.

因此，此时函数f（x）有两个极值点.

当a＜0时，Δ＞0，但g（－1）=1＞0，x1＜－1＜x2，所以当x∈（－1，x2）时，g（x）＞0，f′（x）＞0，f（x）单调递増；当x∈（x2，+∞）时，g（x）＜0，f′（x）＜0，f（x）单调递减.

所以函数只有一个极值点.

（2）略.

评析：本题在对函数求导、整理后决定导函数正负的是分子，分子为二次函数型，因此二次方程根的分布问题就登上了高考的舞台.但二次项系数不确定，故应对其可能情况进行分类讨论.

（1）若a＞0，函数y=f（x）在区间（a，a2－3）上存在极值，求a的取值范围；

（2）若a＞2，求证：函数y=f（x）在（0，2）上恰有一个零点.

解析 ：（1）f′（x）=x2－2ax，令f′（x）=0，即f′（x）=x（x－2a）=0，所以x=0或x=2a.

因为a＞0，所以x=0不在区间（a，a2－3）内，要使函数在区间（a，a2－3）内存在极值，只需a＜2a＜a2－3，所以a＞3.

（2）略.

评析：函数在区间内存在极值点，即其导函数在区间内存在零点，求导后导函数为二次函数型，故问题转化为二次方程根的分布问题.

解析：因为函数f（x）在区间（－1，1）不单调，所以函数f′（x）在（－1，1）上存在零点.而f′（x）=0的两根为a－1，a+1，区间长为2，所以在区间（－1，1）上不可能有2个零点.所以f′（－1）f′（1）＜0，即a2（a+2）（a－2）＜0.

因为a2＞0，所以（a+2）（a－2）＜0，－2＜a＜2.

又因为a≠0，所以a∈（－2，0）∪（0，2）.

评析：本题从表面看，命题形式上有所变化，即函数在区间内不单调，但其本质仍是导函数在区间存在零点问题.通过挖掘隐含条件不难发现在区间内不可能存在两个零点，故减少了分类讨论的情况，优化了解题过程.

综上所述，二次方程实根分布的理论，虽然直观易懂，但在解决高考问题中的作用却不可低估.它不但可以使相关问题的求解直观简洁，富有新意，而且对于培养学生运用函数与方程以及数形结合等思想方法解题的意识大有裨益.因此，在教学中，要注意引导学生重视对教材习题的探究、归纳、总结，进而提升学生对问题的分析、求解能力.