初探互动式教学课堂的案例研究

☉江苏省常熟中学 曹正清

众所周知，陈旧的课堂模式与新课程理念的矛盾日渐凸显，我们急需探究新的课堂教学模式，建立有效甚至高效的课堂模式，以适应新课改的实施.互动式教学可以很大程度上改进呆板没有活力的陈旧课堂模式.互动式教学并没有固定的形式，尤其在课堂中只要最大程度地让学生积极参与课堂教学，融入课堂氛围，让学生成为学习的主人即可.

一、自主探究与巧妙设问的思考

数学课堂中的巧妙设问是互动式教学的重要手段，具有极强的教学艺术，它是联系教师和学生主体地位的纽带，也是激发学生学习兴趣的催化剂.教师的巧妙设问与学生的自主探究是密不可分的，教师在课堂提问中会出现一系列的满堂灌（不给予学生自主探究的时间，而是自言自语，急于给出教师自己的观点和结论，急于应用练题），满堂问（永远都是“是不是”“对吗”“行不行”“清楚了没”等等，得到一丝回应后，直接给出肯定或者否定的回答，根本不理会究竟学生是否真的理解，是否所有的学生都是这样认为的，太过追求偏离的设问，而缺乏对问题本质的探讨），使得课堂教学有氛围却无实效，长此以往，教学的诟病越来越多.因此，巧妙设问，需要在理解学生掌握知识的基础上，重视提问的有效性、适时性、梯度性、启发性、合理安排提问内容，语言简洁明了，根据不同的学生设置不同的问题，积极开展互动式教学，努力提高课堂有效性.

生A（不假思索）：相交、相切、相离.

师：位置关系简单，那么满足的条件呢？

生B：联立方程，得到一元二次方程.当Δ＞0时，相交；当Δ=0时，相切；当Δ＜0时，相离.

师：嗯，很不错，有何理由？

生B（继续回答）：类比直线与椭圆的位置关系得到的结果.

生们：好像不完整？得到的方程有不同的地方？好像是正确的？……（学生在底下发出了不同的意见）

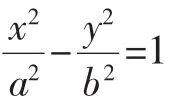
生C：他的回答对了一部分，因为他的回答基于二次项系数不为0的情况下，是正确的.

师：能否完善你们的想法？

生C：当二次项系数为0时，需要重新讨论，即b2-k2a2=0，有一个解，也可以无解，所以也会有相切与相离的情况.

生们：此时不是与渐近线的斜率一样嘛（学生开始踊跃回答）！

生D：此时直线与双曲线的渐近线平行或者重合，平行还是重合取决于m的值.当m=0时，直线与双曲线渐近线重合，此时直线与双曲线没有交点，即相离；当m≠0时，直线与渐近线平行，肯定会有交点，是两个还是一个，有点不清楚？

师：想到这些已经不易，需要鼓励，我想同学的疑问值得大家去探讨，谁会离结果更接近呢？老师拭目以待！（此时的学生们正在草稿纸上分析着，我耐心地等待着结果）

生E：必定相交于一点，因为双曲线无限靠近渐近线，与渐近线的距离越来越近，故与渐近线平行的直线在无限远处不可能出现相交的情况，所以确定只能相交于一点，而且并不是相切的.

师：此时问题已经明朗化，判断直线与双曲线的位置关系，首先区别于椭圆，椭圆与直线联立后的二次项系数恒大于零，故不需要过多的考虑.但是直线与双曲线方程联立后，二次项系数会出现多种情况，因此需要分情况讨论，才能给出正确的解答.同学们，能帮老师总结一下吗？现在老师觉得有点乱乱的？谁能帮忙吗？

生F总结：1.系数为0时，与渐近线重合没有交点，平行于渐近线必相交于一点.2.系数不为0时，判断Δ，Δ＞0时，相交于两点；当Δ=0时，相切于一点；当Δ＜0时，相离.

说明：纵观整个过程，其实作为教师提及5次疑问，简单明了，只是在不经意间表露自己的疑惑和问题的存在性，尽管没有华丽的语言来描述，但是，积极配合学生的质疑以及探究，将问题一步一步明朗化，因此，学生的自主探究，教师的巧妙设问，学生的深思熟虑，让互动式教学体现了它的生动化，提高了课堂的有效性.

二、合作交流与反思感悟的结合

合作交流与反思感悟是新课程理念下必须具备的要求，其不仅是学生学习的需要，也是促进互动式教学最好的平台之一.所谓合作交流，就是指教师与学生在课堂中共同完成学习任务，按照既定目标，采取的互助型学习交流.学生在学习过程中，需要与同学、教师之间形成完美的互动，擦出思维的火花，从而促进知识的形成.所谓反思感悟，是指学生与教师在合作交流的过程中出现的问题，或者是新理念的形成，需要及时总结，认真整理，指导以后学习中可能出现的问题.当然开展合作交流，反思感悟，并不是无目的地浪费时间，而是有针对性地解决与内容密切相关的问题.

案例2：《二次函数求最值》

例题：求二次函数y=x2+2x+3，x∈R的最值.

生A：配方得到：y=（x+1）2+2，当x=-1时，ymin=2，无最大值.

变试1：求二次函数y=x2+2x+3，x∈［-3，0］的最值.

生B：配方得到：y=（x+1）2+2，当x=-1时，ymin=2，当x=-3时，ymax=6.

师：上述两类问题，大家在初中时已经非常熟悉，我们的方法是：通过配方，得到解析式；根据图像中对称轴的特点分析最值即可.

变式2：求二次函数y=x2+2ax+3，x∈R的最值.

生C：配方得到：y=（x+a）2-a2+3，当x=-a时，ymin=-a2+3，无最大值.

变3：求二次函数y=x2+2ax+3，x∈［-3，0］的最值.

生D：配方得到：y=（x+a）2-a2+3，然后通过图像来讨论，对称轴为x=-a……

师：好像遇到了难题了，对称轴究竟在区间的哪个位置不确定？轴动区间定，那么该如何解决？我们分组交流，大家各抒己见吧.（学生以小组形式进行讨论）

A组交流成果：求最小值时，我们把对称轴放在已知区间的左边（-a≤0），中间（-3＜-a＜0），右边（-a≥-3）三种情况，将区间定格，对称轴移动即可.求最大值时，我们也分成以上三种情况去解决.

B组交流成果：求最小值时，我们利用物理中的相对论，将原本动的对称轴定下来，移动本来定的区间，我们得到了一幅类似于机器脸的图形，更加生动形象，但是结果跟A组是一样的.在求最大值时，我们遇到了问题，像A组一样的分类，对称轴在区间中间的部分好像还需要分情况讨论，这个结果有些不明确了.

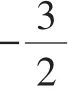
D组总结：最小值可以-3，-a，0处均可以取得最小值，所以肯定分三种情况；最大值却只能在-3和0处取得，所以只需要分两种情况.

说明：学生们的自主探讨，以及教师适时的点拨，使得问题的解决非常顺利，而且学生与教师的互动形成了较好的效果，提高了课堂的效率.“轴动区间定”这个难题也得到了充分形象的解释，特别是机器脸的提出，大大提高了学生对本块内容的认知.因此，适时的合作交流以及交流中不断的反思感悟，促进了互动式教学的顺利开展.

总之，互动式教学不应拘泥于课堂问题的解决，它可以贯穿整个教学过程.课后的复习与反思，在解决完“轴动区间定”的问题后，我们可以带着问题去研究“轴定区间动”的问题，学生可以自主交流，也可以与教师形成互动，为解决此类问题提供充分的思考空间.多媒体技术日新月异，学生与教师的互动不一定需要面对面的交流，可以通过QQ组群等讨论数学中出现的问题，以便及时解决，也可以与教师谈谈学习心得体会，多设疑教师可以多答疑，使得课堂不再受时间与空间的制约，真正体现了互动式教学的宗旨，从而为提高课堂有效性作出较大的辅助贡献.

1.方明.陶行知教育名篇［M］.北京：教育科学出版社，2005.

2.姜兴荣.探求解题思路的几种有效策略［J］.中小学数学，2013（7-8）.

3.朱永祥.再谈数学思想方法的挖掘和应用［J］.中学数学（上），2008（2）.