最小系数排序法在汽车认证项目进度管理方面的应用

邱创国 张文光

(上海交通大学机械与动力工程学院，上海 200240)

0 引言

中国汽车产业近年来发展迅速，汽车在普及的同时也带来了一系列交通安全、环境污染和能源消耗等问题。为应对这些问题，政府主管部门频频推出针对汽车安全、环保、节能的新法规，这些法规普遍具有强制性。而汽车认证是为了证明汽车的各项性能满足相关法规的强制性要求或达到一定技术指标所进行的一系列质量验证活动，它是汽车跨入市场的一条必经之路，也是新车型进入销售环节的一道“紧前工序”。汽车认证项目的周期长短通常左右了相关车型的入市时间节点和市场销售时间，进而影响车企对市场机会的把握和销售目标的实现。在竞争日趋激烈的条件下，车企产品更新换代速度以及应对法规变更的响应能力很大程度上受到汽车认证周期的影响，因此，缩短汽车认证项目周期对车企来说具有十分重要的意义。

汽车认证项目的周期管理属于项目进度管理范畴。传统项目进度管理方法在汽车认证项目中的应用较普遍，如甘特图，关键路径法(CPM)，计划评审技术(PERT)，工作分解结构(WBS)，项目里程碑管理(Milestone)等。近年来，很多学者基于约束理论(TOC)［1］，研究了资源约束下的项目进度管理 (Resource Constraint Project Scheduling Problem，RCPSP)，这是当前项目进度管理研究的一个重要方向。RCPSP 把项目的时间管理和项目的资源管理有机地结合起来，通过研究项目的关键约束，寻找在满足约束条件下的最优资源调度方案，进而弱化或消除项目关键约束的负面作用，最大化地实现项目设定的一系列目标。在常见的RCPSP 中，任务的逻辑约束一般表示为先后序约束，即任意任务必须在其后续任务开始之前完成，也可以简称为结束- 开始(Finish-Start)关系［2］。任务排序其实就是在特定时间把机器的处理时间以一定量分配给特定的任务，它是资源分配问题中的特殊类型，因此任务排序的优化是资源约束下进度管理的一条特殊思路。在汽车认证项目进度管理中，PERT 方法通常应用于估计各项活动的时间长度，以及协助项目资源的合理调度［3］。关键路径法用来识别项目活动中的最长活动序列，找出影响项目总周期的各项活动，通过缩短关键路径上的活动历时来最小化项目的总周期［4］。项目的里程碑管理在汽车认证项目中通常与WBS 结合起来运用，便于项目总体进度的把握，及时纠偏和分散项目的进度风险［5］。资源约束下的进度管理深刻地描述了资源与进度的密切关系。以上这些方法在项目进度管理中的功能不同，各有侧重，然而，在缩短汽车认证项目周期方面，这些方法和理论显得缺乏针对性或目标导向性，无法具体地回答资源约束条件下，如何充分利用汽车认证项目所具有的突出特点，以项目进度目标为导向，合理地分配项目的瓶颈资源，使项目进度最优。而这正是本文所要研究的课题。

1 汽车认证项目的特征

汽车认证项目是具有明显特征的项目类型。从总体上看，汽车认证项目具有周期长，资源投入大，涉及部门多，空间跨度大，前后工序的相互依赖性强等特点。从项目内涵上看，通常包含多项同时可开展的任务;各项任务具有共同的流程，且在流程上有三个以上的执行部门;各项活动的历时是已知的。从项目约束上讲，在时间、成本、质量［6］方面侧重于时间约束，其资源约束主要包括活动执行部门的可支配时间，样车数量，实验室设备场地资源，可利用的资金等;时间约束则包括项目总周期，各项活动历时等;此外，汽车认证项目还有流程约束，活动相互之间的逻辑顺序不能改变等特征。可见，汽车认证项目的约束类型属于一种混合型约束。

2 最小系数排序法介绍

在对汽车认证项目进行优化排序前，必须明确几个已知条件，即项目的任务数量，流程上一共有几个活动执行部门，各项任务在每个执行部门的活动历时，这些活动历时一般是可预知的，可以通过专家评审进行客观估计。剩下的问题就是如何对项目的若干个任务进行合理排序，以此充分利用项目活动执行部门的处理能力和可支配的有效工作时间，减少部门之间的互相等待，进而加快项目进度和缩短各项任务的平均流程时间。

2.1 排序问题

排序问题源自于生产车间，传统的排序问题通常分为单机问题、双机问题、多机问题，通过求解加工的最优排序来实现一系列生产目标。求解排序问题时，只有少数的问题类型存在求取最优解的有效算法。从20 世纪60 年代以来，人们发现越来越多的排序问题是困难问题(NP)［7］。尤其当机器台数达到三台以上，求解该类问题较多采用启发式算法，虽然该算法获得的结果并非最优解，但在生产的实际中，启发式算法仍然具有非常重要的应用意义，在可接受的成本条件下实现了一定程度的排序优化，带来了明显效果。

2.2 n 项任务在单台机器上的排序

针对单机问题的排序，目前主要依赖于基于优先权的排序方案［8］，比如最短活动历时优先(SPT)，最小松弛度优先(SST)，最早交货期优先(EDD)，关键比率最小优先(SCR)，等等。

除此之外，也可以通过数学方法进行求解，单机排序问题的数学模型［9］可以表示为:n 个加工量为{di，i=1，2，…，n}的工件在一台机器上加工，Ct为机器在第t 时段的工作能力，则完成所有产品加工的最少时段数的数学模型为

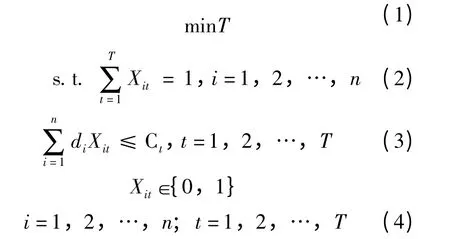
式(1)要求加工所用的时段数(T)最少;式(2)、式 (4)中，Xit，T 均为决策变量，Xit=1 表示第t 时段加工产品i;式(3)表示每个时段的加工量不超过工作能力的限制，其中di表示工件一定在某一时段t 加工。

2.3 n 项任务在多台机器上的排序方法

针对两台机器的排序问题，Johnson 提出的约翰逊法被公认为两台机器的最优调度［10］。而对于三台机器的排序问题，曾出现过多种算法，并把它列为NP 完备问题。而对于三台以上机器的排序问题，目前仍以启发式算法为主。最小系数排序法为其中一种较简便的方法。

最小系数排序法一般被描述为n 项任务在m台机器上的排序方法。其步骤如下［11］:

(1)确定中间机器或中间线。

(2)计算排序系数Ki。

(3)按照最小排序系数，由小到大依次排序，最小者最先安排加工。

排序系数Ki为某个工件在前半部分机器上加工时间与在后半部分机器上加工时间的比值。

3 应用实例

2012 年F 公司为丰富公司的产品线提出W项目，计划在中国市场引入5 款新车型，5 款车型代码分别为A，B，C，D，E。项目任务是在最短时间内完成5 款车型的认证，并尽量缩短每款车型的流程时间。中国汽车认证项目的内容分为四大部分，即认证申请，参数审核，实车测试，型式批准。这四部分任务必须按顺序依次完成，不能跨越任何步骤，因此它也构成了汽车认证项目的基本流程。根据汽车认证项目的基本流程和各项活动执行部门的分工，对汽车认证的任务进行WBS 分解，分解后WBS 见图1，项目流程一共分为9 个步骤。

根据实际工作内容，采取专家评审法对W项目的各项任务的活动历时进行估计见表1。

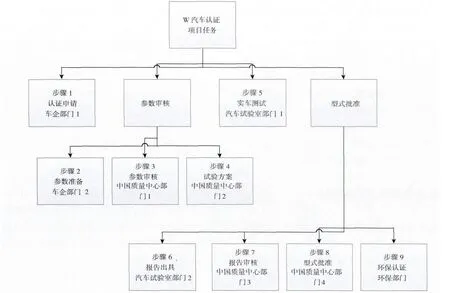
图1 汽车认证项目的WBS 分解

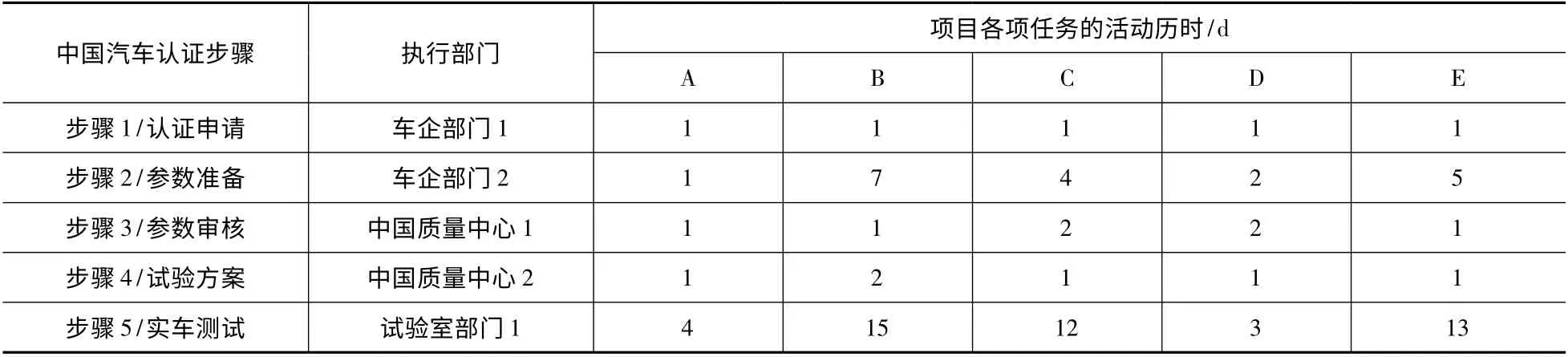
表1 中国汽车认证项目各项任务的活动历时表

(续)

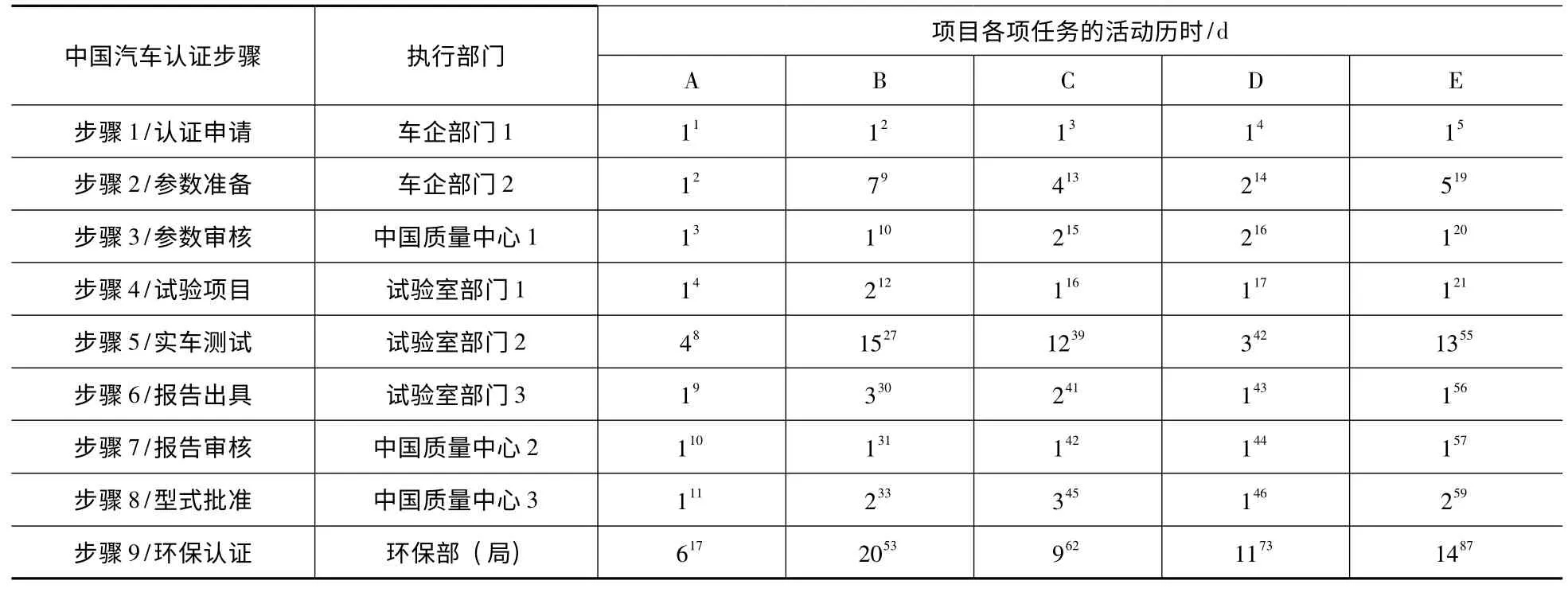
表2 按随机排序的项目时间计算

表2 显示，这个项目具有5 个同时处于可开展状态的任务，每项任务的流程相同，每个步骤对应不同执行部门，各项活动历时已知，项目的流程共有9 个步骤，分别由9 个活动执行部门负责，项目不同车型(任务)的活动历时存在较大的差异。显然，这是一个排序问题。按照康维提出的4 个参数表示法可表示为

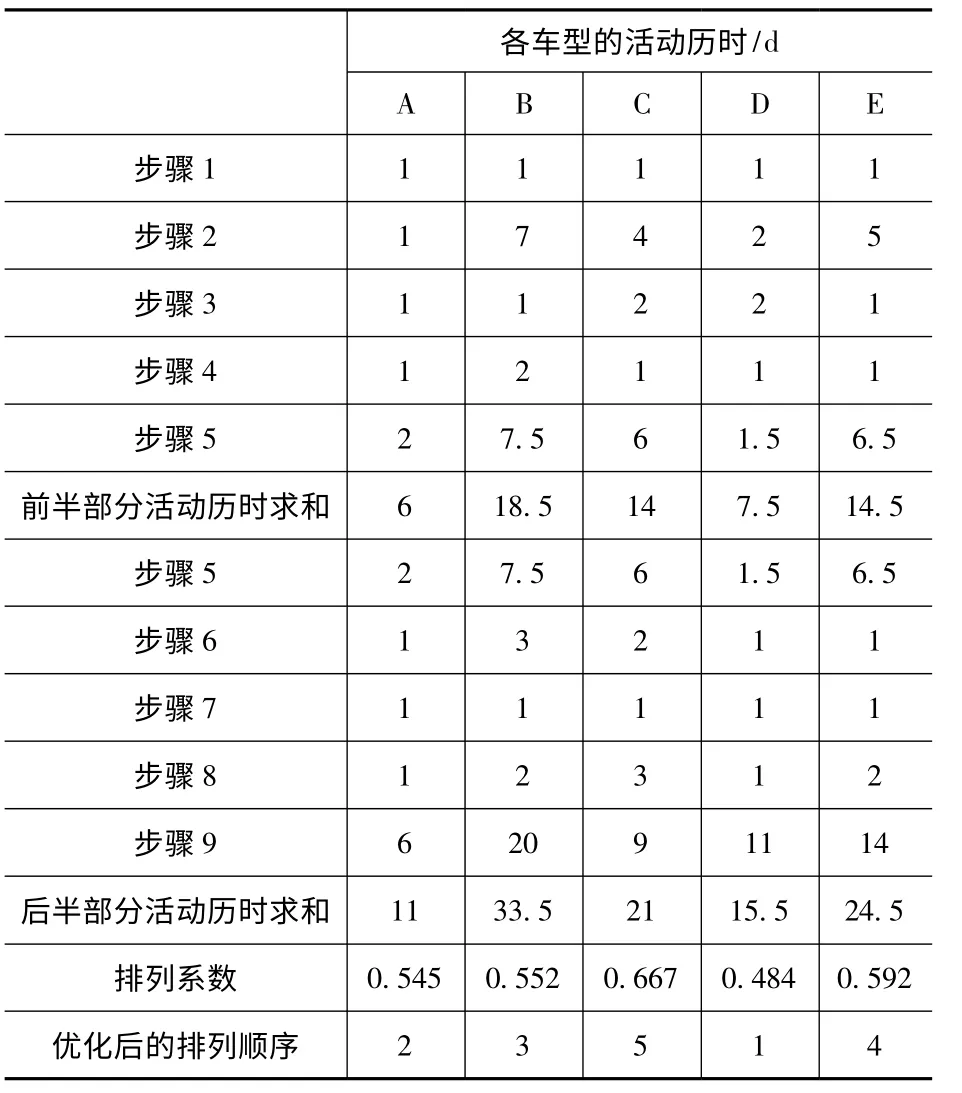
表3 按最小系数法计算排序系数

式中，5 表示任务数为5;9 表示执行部门(机器)数为9;F 表示排序问题的类型，流水型用“F”表示;T 表示优化目标，即最小化项目总周期和任务平均流程时间。

目前的做法是按照正常(随机)排序A—B—C—D—E 依次开展认证活动。

如表3 所示，通过表上作业法，可以迅速地得出W 项目的总周期为87d，即项目的最后一个任务E 的完成时间为87d。W 项目5 项任务的流程时间分别为:A 为17d，B 为53d，C 为62d，D 为73d，E 为84d，平均流程时间为58.4d。5个任务流程时间即为5 款车型的上市时间。

然而，这个时间是否还存在压缩改善的空间呢?对此可以尝试通过改变5 个车型的认证顺序，分析W 项目的总周期和它的5 个任务的流程时间是否缩短。

下面采用最小系数法，对W 项目的5 个任务进行重新排序。

表4 把项目的9 个步骤的活动历时平均分为上下两部分，上半部分包含步骤1 ～4 和步骤5的50%活动历时，下半部分包含步骤6 ～9 和步骤5 的50%活动历时，根据式(5)对上下两部分的活动历时分别进行求和，用上半部分的活动历时总和与下半部分的活动历时总和的比值作为排列系数，最小的排在最前面。根据表4 的计算结果显示，D—A—B—E—C 为优化排序。

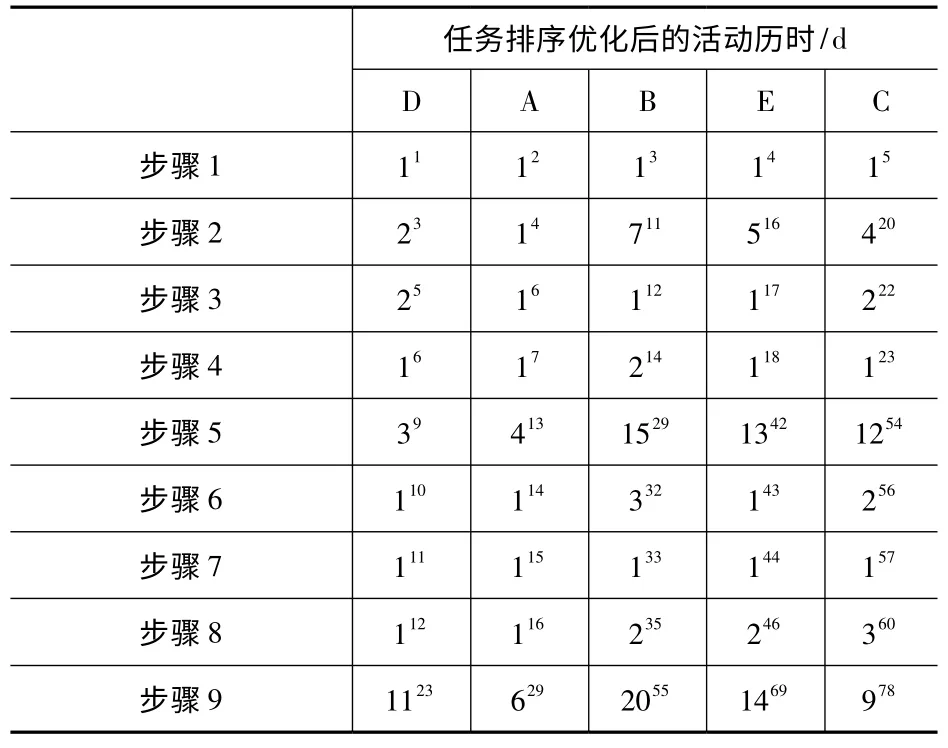
表4 按最小系数排序的项目时间计算

如表5 所示，通过表上作业法得出W 项目的总周期为78d，即项目的最后一个任务E 的完成时间为78d。W 项目5 项任务的流程时间分别为:A 为23d，B 为29d，C 为55d，D 为69d，E为78d，5 项任务的平均流程时间为50.8d。

表5 显示，优化后项目的总周期从原来的87d 缩短为78d，缩短了9d。项目总周期缩短10.34%。项目5 项任务平均流程时间优化前为58.4d，优化后为50.8d，优化天数:7.6d，优化幅度达到13.01%。

根据F 公司市场部评估预测，5 款车型的年总销售额在4 万台左右，即全国日平均销售量在100 台以上。保守认为每台利润为2 万元人民币，那么，通过优化排序，仅项目总周期所缩短的9d便能为车企一年带来1800 万元人民币的额外利润。此外，W 项目5 款车型比原来平均提前7.6d 进入市场销售，还各自带来额外的销售额。

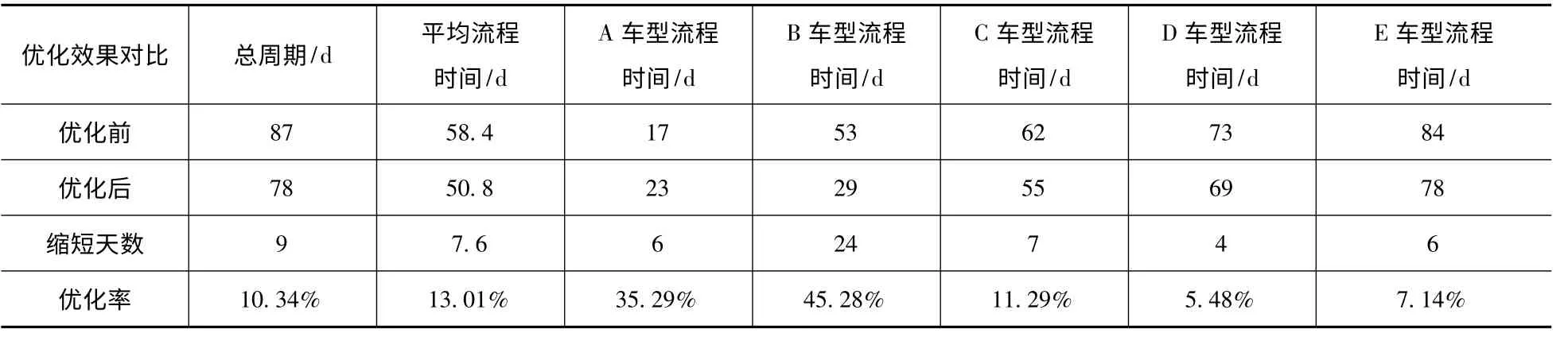
表5 优化效果

4 结语

在汽车认证项目的进度管理中，首先，采用最小系数排序法对任务进行优化排序，有效地缩短了项目的总周期和各项任务的平均流程时间。在运用时须对项目的特征与约束进行深入研究，当项目的某些条件发生改变时，应该考虑该条件的改变是否对该方法产生影响。其次，在运用最小系数排序法对项目的各项任务进行排序前，需要运用WBS、PERT 等经典的方法技术对汽车认证项目的任务内容、活动流程、活动历时等进行一系列预处理，使之转化为一个可处理的排序问题并进行优化。理论和实践证明，使用最小系数排序法对项目的任务进行排序，能高效调配汽车认证项目的关键资源，降低瓶颈资源的负面制约效果，使项目中各个执行部门的处理能力和处理时间得到充分利用，减少部门之间的互相等待，从而缩短整个项目的总周期和项目各项任务的平均流程时间。这种方法能为汽车企业的项目进度管理带来积极的效果。

［1］ Rand G K. Critical chain:the theory of constraints applied to project management ［J］. International Journal of Project Management，2000，18 (3):173-177.

［2］ 郑元利. 基于工位的资源受限项目调度问题的模型研究与调度算法实现［D］. 北京:北京交通大学，2014.

［3］ 高立娥，康凤举，刘卫东，等. 基于时间Petri 网的实时多任务调度方法研究［J］ . 系统仿真学报，2006 (11):3075-3077，3147.

［4］ Steyn H. An investigation into the fundamentals of critical chain project scheduling ［J］ . International Journal of Project Management，2000，19 (6):363-369.

［5］ 汪若洋. 项目进度管理方法及其应用研究［D］. 郑州:解放军信息工程大学，2013.

［6］ 王健，刘尔烈，骆刚. 工程项目管理中工期-成本-质量综合均衡优化［J］. 系统工程学报，2004，19 (2):148-153.

［7］ 李好好. 若干排序问题的研究［D］ . 杭州:浙江大学，2014.

［8］ 何正文，贾涛，徐渝. 求解资源约束项目调度问题的启发式算法综述［J］. 运筹与管理，2007，16 (3):78-84.

［9］ Garey M R，Johnson D S. Computers and intractability:a guide to the theory of NP-completeness ［M］ . New York:Freeman，1979.

［10］ S M Johnson. Optimal two and three stage production schedules with setup times included ［J］ . Naval Research Logistics Quarterly，1954 (1):61-68.

［11］ 谢柏林. 简易排序方法:最小系数法［J］. 管理现代化，1983 (1):19，22. PMT