输水隧洞TBM施工工期全局综合敏感性分析

王晓玲，赵梦琦，洪 坤，毕 磊

(天津大学水利工程仿真与安全国家重点试验室，天津 300072)

与普通隧道工程相比，输水隧洞具有洞线长、地质条件复杂、施工技术及机械配置要求高、工期长等特点[1]，因此其施工过程中出现实际工期与计划工期不符情况的概率更高，给施工进度安排与管理带来一定难度．现阶段国内外对输水隧洞 TBM(tunnel boring machine)施工工期不确定性的研究多集中在发现并确定引起工期不确定性的因素，并对这些因素加以控制上．国内的文献[2-7]采用不同方法验证了输水隧洞 TBM 施工工期具有不确定性．在此基础上，温森等[8]进行了 TBM 施工进度风险评估分析；赵延喜等[9]用事故树方法识别出引起工期不确定性的仿真参数．国外的文献[10-16]也都指出了一些引起工期不确定性的具体因素并进行了验证，但研究范围多为隧道工程，极少针对水利工程的输水隧洞 TBM 施工，并且以上分析局限于对工期不确定性及相关影响因素的定性判断，定性结果无法反映各因素对工期不确定性的影响程度，弱化了对施工进度安排与管理的指导作用．为此，Touran等[17]对隧洞 TBM 施工过程中的掘进速度进行了敏感性分析，但仍属于单因素敏感性分析．

综上所述，现阶段国内外的研究多集中在识别和判定施工参数对工期不确定性有影响这一问题上，没有对引起工期不确定性的关键影响因素做进一步分析，少数对工期不确定性现象进行敏感性分析的研究也局限在单因素敏感性分析上．然而，除各工序段的工期外，影响总工期的因素既包括岩性、错车时间等自然界的或带有随机性的不可控因素，也包括机械配置这种可人为确定、但取值不唯一的因素．其中，前者叫做不确定性因素[18]，后者叫做关联因素[19]．输水隧洞 TBM 施工工期是受岩性相关参数、活动持续时间等不确定性因素和列车辆数等关联因素影响的具有不确定性的复杂系统．因此，对输水隧洞 TBM 施工过程中工期的不确定性现象进行基于全局综合敏感性分析法的正交试验设计[20]是很有必要的．

本文针对输水隧洞 TBM 施工系统的工艺特征和影响因素，依托输水隧洞 TBM 施工仿真模型，采用基于全局综合敏感性分析法的正交试验设计，在既考虑参数主效应对工期不确定性的影响，也考虑参数间耦合效应对其影响的条件下，对输水隧洞 TBM 施工存在的工期不确定性现象进行分析．以某引水式电站的输水隧洞 TBM 施工过程为例，首先，研究施工仿真模型中全部参数的主效应对工序工期与总工期不确定性的影响程度的定量数据；其次，研究工序工期主效应对总工期不确定性的影响程度的定量数据；最后，综合分析参数的耦合效应对总工期不确定性的影响，为施工组织计划的合理安排和施工机械配置方案的优选提供科学依据．

1 正交试验设计原理

1.1 试验的统计度量

正交试验设计是 20世纪 20年代由英国统计学家费希尔提出的，与全面试验相比，该方法是一种高效处理多因素优化问题的科学计算方法，下面通过一个例子来说明这个情况．

做一个3因素3水平的试验，图1为3因素3水平全面试验与L9(34)正交试验设计的试验次数对比，图中字母 A、B、C 代表 3 个因素；A1、A2、A3、B1、B2、B3、C1、C2、C3代表各因素的因素水平．按全面试验要求，需进行33＝27种组合的试验(图1立方体中每1个交点表示 1次试验)，且尚未考虑每个组合的重复数．若按正交表 L9(34)设计安排正交试验只需进行9次试验(图1立方体中用黑色正方形标注的交点需要进行正交试验)，按 L18(37)设计只需进行 18次试验，工作量大大减少．

图1 3因素 3水平全面试验与 L9(34)正交试验设计的试验次数对比Fig.1 Comparison of test number of comprehensive test and orthogonal test design with three factors and three levels

输水隧洞 TBM 施工过程涉及的施工参数较普通隧道工程更多，也更复杂，且每个参数的可能取值也不少，对其工期不确定性进行的敏感性分析属于多因素、多水平的综合敏感性分析．若对所有待分析因素的全部因素水平进行敏感性分析，工作量将过于庞大，在实际工程中缺乏可操作性．正交试验只从每个待分析因素中选取部分有代表性的因素水平进行分析，并在分析过程中以正交性为依据，既保证任一因素的各水平做相同数目的试验，也保证任两个因素的水平组合做相同数目的试验．这样，用部分数据代表全体数据得出的分析结果是有效的．因此，正交试验设计可以有效解决在对输水隧洞 TBM 施工工期不确定性进行的敏感性分析中待分析因素的因素水平过多的问题．

1.2 正交表及其性质

正交表是正交试验设计的基本工具，1951年日本统计学家田口玄一将正交试验选择的水平组合列成表格，形成正交表．正交表是一整套规则的设计表格，其代号表示为 Ln(qm)，其中：L代表正交表；n为试验次数；q为因素水平数；m为因素个数，在正交表中代表其列数．正交表需要满足两条基本设计要求：①任一个因素的各水平做相同数目的试验；②任两个因素的水平组合做相同数目的试验[21]．

正交表分为两种：同水平正交表和混合水平正交表．同水平正交表是指该正交表中各因素的水平数相等，例如 L9(34)，它表示需做 9次试验，最多可观察4个因素，每个因素均为3水平；混合水平正交表是指该正交表中各因素的水平数不完全相等，例如L8(41×24)，它表示需做 8次试验，最多可观察 5个因素，而5个因素中有1个因素为4水平，其余4个因素为 2水平．采用这种正交表可以很方便地设计出水平数不同的多因素试验，但有时无法考察因素之间的耦合效应[21-22]．而同水平正交表既可以使每个因素的不同水平以相同的次数出现在每列中，也便于考察设计因素之间耦合效应．本文对工期不确定性的分析，要同时考虑参数的主效应与耦合效应，因此选用同水平正交表．

1.3 试验的统计模型和数据分析

本文采用方差分析法对正交试验设计的试验数据进行分析．所谓方差分析法，就是通过研究不同来源的变异对总变异的贡献大小，从而确定因素对研究结果影响程度的一种数学方法．这种方法可将因素水平或耦合效应的变化所引起的试验结果的差异与误差波动所引起的试验结果的差异区分开来，即

式中：TS为总平方和；AS为组间平方和；eS为组内平方和．式(1)中各变量的计算公式为

式中：m为因素数量；ijx为第i个因素在该因素的第j个水平上的结果；ix为第i个因素在该因素所有水平上结果的平均值．

自由度指计算某个统计量时，取值不受限制的变量个数，总平方和的自由度为( 1)mq- ，组间平方和的自由度为( 1)m- ，组内平方和的自由度为 ( 1)mq- ．平方和除以自由度即可得均方差

一般取置信区间为 95%，若 F ≤ 0 .05，则认为某因素或因素间耦合效应对结果不确定性的影响是显著的；反之，则认为不显著．F越小说明因素的显著性越高.

2 输水隧洞TBM施工仿真模型

2.1 模型的建立

图2为输水隧洞TBM施工仿真模型．输水隧洞TBM 施工工程是由一系列单项工程组成的，称为施工工序，每个施工工序又是由掘进、支护、排运等各个具体活动组成的反复循环过程．根据工程施工的以上特点，仿真模型被划分为两个层次：单元模型层与工序模型层．单元模型层采用 CYCLONE模型进行单元施工仿真；工序模型层采用 CPM 网络模型进行工序施工仿真，并且单元模型构成工序模型，工序模型构成整体系统模型[23]．由仿真模型的结构特点可知，输水隧洞 TBM 施工过程更为复杂，如果仅仅对普通隧道工程的施工工期进行敏感性分析，分析结果不具有指导输水隧洞工程 TBM 施工的实际意义.因此有必要针对输水隧洞工程的特殊工艺特点，在细致研究输水隧洞复杂施工过程的基础上，再对其工期进行敏感性分析，从而得出能够应用于实际工程中的、有指导意义的分析结果．

图2 输水隧洞TBM施工仿真模型Fig.2 Simulation model for water-conveying tunnel TBM construction

由于掘进等活动持续时间的随机性和机械配置方案的不唯一性，工序工期具有不确定性．相应地，随着工序工期的变化，总工期也具有了不确定性．因此，要研究输水隧洞 TBM 施工工期的不确定性，既需要分析仿真模型中各参数对工序工期不确定性的影响，也需要分析工序工期对总工期不确定性的影响[24]．因此，建立数学模型如下：式中：M代表理论方法，包括 CYCLONE循环网络建模方法 MCO、CPM 循环网络建模方法 MCM和工期不确定性分析方法 MU；P代表M的参数集合，包括输入参数I与输出参数O；PCO中包括岩性参数 IL、结构参数 IS、施工参数 IB、设备参数 IE等输入参数和输出参数工期 OD；PCM包括仿真工序 ISIM、非仿真工序 IO等输入参数和输出参数持续时间 OT；PU中包括关联因素 IA、不确定性因素 IU两类输入参数和主效应 OM、耦合效应 OC等输出参数．定义函数 f1、f2和f3以表示不同组参数间的逻辑关系，f1描述 MCO和MU之间的逻辑关系；f2描述 MCM和 MU之间的逻辑关系；f3描述 MCO和 MCM之间的逻辑关系．

2.2 输入参数分析

施工过程中，列车辆数等资源信息的配置情况可以被人为改变，而资源信息的改变意味着施工机械配置方案的变化，不同施工机械配置方案下的施工工期可能会不同，因此列车辆数等资源信息属于具有不唯一性的会引起工期不确定性的关联因素；对于不同的岩性条件，TBM具体施工工艺不同，即输水隧洞岩性的不确定性会相应地引起 TBM施工参数的变化，使施工参数也具有了不确定性，则施工参数属于会引起工序工期不确定性的不确定性因素；工序施工仿真模型的输入参数中还包括一类活动持续时间(如卸渣时间)，活动持续时间是带有随机性的，会引起工序工期的不确定性，因此活动持续时间属于具有随机性的会引起工序工期不确定性的不确定性因素．

综上可知，研究工期不确定性须进行考虑岩性相关参数、活动持续时间等不确定性因素和列车辆数等关联因素的多因素的综合敏感性分析．

3 输水隧洞 TBM施工工期全局综合敏感性分析

采用基于全局综合敏感性分析法的正交试验设计分析输水隧洞 TBM 施工工期的不确定性现象分为如下4个步骤．

(1) 确定因素以及因素水平．将模型中全部关联因素与不确定性因素确定为正交试验设计的待分析因素．模型参数按性质划分为3类[25]：第1类是确定型参数，这类参数反映原型系统运行特征属性，在系统运行过程中不变，如隧洞洞长；第 2类是随机型参数，这类参数在系统运行过程中不确定但遵循某种统计规律，如卸渣时间；第 3类是模糊型参数，这类参数在仿真系统中必不可少，但取值不是完全确定的，如列车辆数．第2、3类参数是关联因素和不确定性因素的来源，为正交试验设计的待分析因素．根据因素取值范围和服从的分布函数，随机确定3个或以上取值作为因素的因素水平．

(2) 建立正交表．根据因素个数与因素水平数，挑选合适的正交表(也可自行设计)，并设计表头．所建立的正交表要满足两个要求：①任一个因素的各水平做相同数目的试验；②任两个因素的水平组合做相同数目的试验．

(3) 计算施工工期．将正交表中的试验方案逐个输入仿真模型，运行仿真程序并记录输出结果．

(4) 对结果进行方差分析．计算因素主效应和因素间耦合效应的显著性水平，设置置信区间，对结果进行排序与筛选：首先，进行工序工期对总工期不确定性、参数对工序工期不确定性的主效应分析，确定在实际施工中需要重点控制的施工工序与施工参数；其次，比较参数对工序工期和对总工期不确定性的主效应分析结果，根据两组显著性水平趋势，总结出各施工参数对工期不确定性影响的规律；再次，在主效应分析结果的基础上，进行参数对总工期不确定性的耦合效应分析，达到控制不同施工机械之间的搭配情况的目的，对施工方案进行二次优化．

4 实例分析

选取某引水式电站的输水隧洞关键路线段 TBM施工过程为研究对象，输水隧洞工程面貌如图 3所示，该隧洞段长12.96,km，直径9.6,m，采用1台双护盾TBM机施工．

经由初始仿真计算，得到图 4所示的输水隧洞TBM 施工初始仿真横道图，整个输水隧洞施工过程包括 14个 TBM 施工的工序段，工序工期取值范围见图5．施工过程中涉及到的参数共有11个，每个参

图3 输水隧洞工程面貌Fig.3 Lineament of water-conveying tunnel project

图4 输水隧洞TBM施工初始仿真横道图Fig.4 Initial simulation Gantt chart of water-conveying tunnel TBM construction

数都有引起工期不确定性的可能，因此需要分析全部11个施工参数对工期不确定性的影响．其中，取值不唯一、但可人为确定的资源配置参数有列车辆数、渣车数和渣车容量，属于关联因素；其余参数中，掘进速度和换刀率受岩性条件的影响，停机时间等活动持续时间带有随机性，都属于不确定性因素．敏感性分析输入参数取值范围见表1．

图5 工序工期取值范围Fig.5 Ranges of process duration

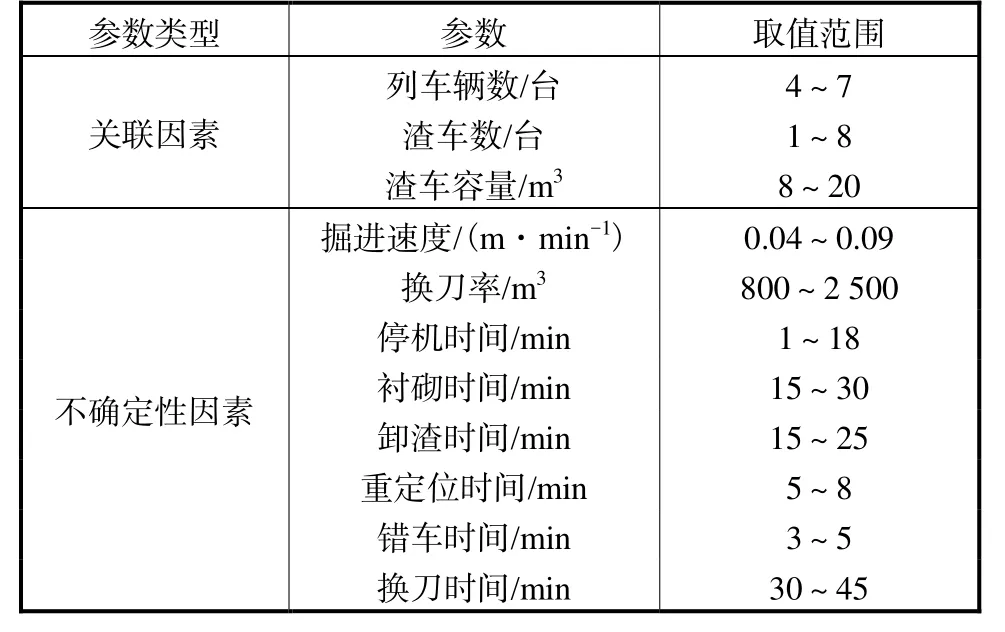
表1 敏感性分析输入参数取值范围Tab.1 Ranges of sensitivity analysis input parameters

根据正交试验设计，确定工序工期主效应对总工期不确定性影响的显著性水平，如图 6所示．本文设置 95%置信区间，则存在 4段敏感性工序段，且敏感度排序为第1段＞第2段＞第6段＞第3段．选取最敏感的第1段工序，分析参数主效应对工序工期不确定性影响的显著性水平，结果如图 7所示，存在 3个敏感参数：掘进速度、停机时间和衬砌时间，且其显著性水平均为 0．因此，在实际施工中，该工程可通过对 TBM 施工工序段中的第 1、2、3、6段的进度控制来优化总工期，同时在此4个工序段的施工过程中，需注意掘进速度、停机时间、衬砌时间这 3个施工参数的选择．

图6 工序工期主效应对总工期不确定性影响的显著性水平Fig.6 Significance level of process duration’s main effect on total duration uncertainty

图7 参数主效应对工序工期不确定性影响的显著性水平Fig.7 Significance level of parameters’ main effect on process duration uncertainty

下面分析参数主效应对总工期不确定性影响的显著性水平，结果如图 8所示．对比图 7和图 8发现，参数主效应对工序工期和总工期不确定性的影响程度呈现出趋势的一致性，因此可总结如下规律：掘进速度、停机时间、衬砌时间对输水隧洞 TBM 施工工期不确定性影响显著，不论在哪个施工阶段其取值都应重点考虑；卸渣时间、列车辆数、换刀率和重定位时间对工期不确定性有影响，但并不显著，在两个施工阶段中取值可酌情考虑；渣车数、渣车容量、换刀时间和错车时间对工期不确定性影响较不显著，在选取这几个参数的取值时，无需考虑其在施工进度方面对工程的影响．

最后分析参数耦合效应对工期不确定性影响的显著性水平，结果如图9所示(11个参数耦合效应的显著性水平只有 1个数据F＝0.047，因此不绘制在图9中)．2个参数到11个参数耦合效应的分析结果中都存在显著性水平小于 0.05的参数组合，这说明在实际施工中，不仅需要注意敏感性施工参数对工期不确定性的影响，也需要注意不同施工参数的水平组合对其的影响．对该结果做进一步分析，在各组参数组合中分别筛选出敏感性最强的参数组合．已知敏感度＝1－显著性水平(单位：%)，图 10为参数耦合效应敏感度最大值．比较该结果可知，6个参数的耦合效应对工期不确定性的影响最显著，这 6个参数为：掘进速度、停机时间、衬砌时间、卸渣时间、重定位时间和错车时间．因此，在合理化不同机械设备之间的搭配组合时，应首先重点控制的是上述6个施工参数所对应机械设备的配套情况，从而达到进一步优化施工组织计划的目的．

图8 参数主效应对总工期不确定性影响的显著性水平Fig.8 Significance level of parameters’ main effect on total duration uncertainty

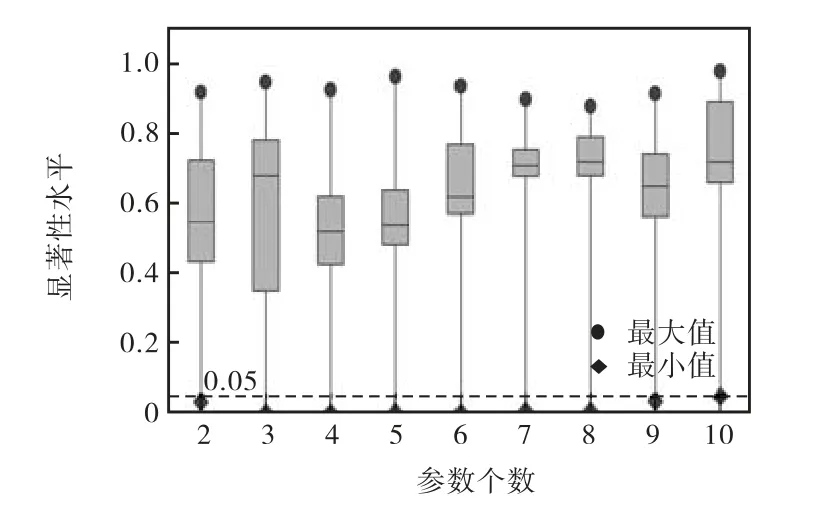
图9 参数耦合效应对工期不确定性影响的显著性水平Fig.9 Significance level of parameters’ couplingeffect on duration uncertainty

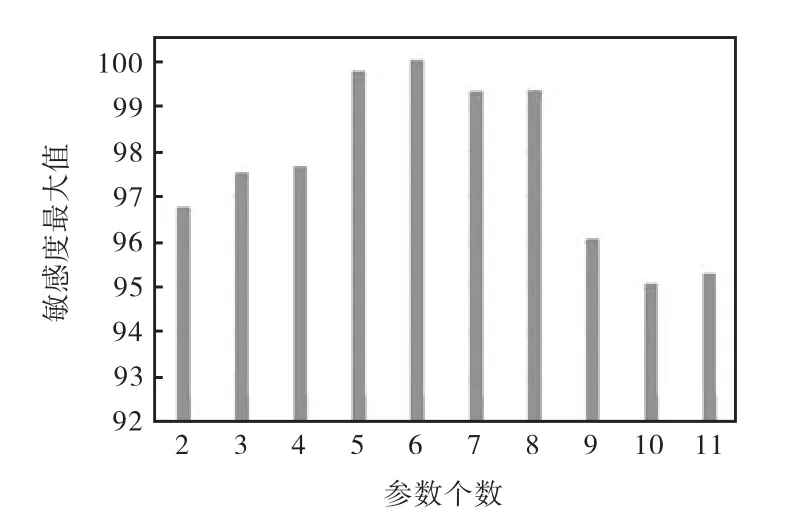
图10 参数耦合效应敏感度最大值Fig.10 Maximum sensitivity of parameters’ coupling effect

将分析结果与工程实际数据进行验证．取该工程中 5组 100,m洞段施工参数与工期列于表 2中.首先，由表中实际工期与仿真工期对比可知，输水隧洞 TBM 施工仿真模型的仿真结果与实际工期吻合度较高，仿真结果具有指导实际的可信度．其次，由表2可知：洞段1的掘进速度比洞段2大很多，其他施工参数相同，而洞段1工期比洞段2少2,d；洞段2的停机时间比洞段 4小较多，其他施工参数相同，而洞段2工期比洞段4少1,d；洞段3的衬砌时间比洞段5小较多，其他施工参数相同，而洞段3工期比洞段5少1,d．由于洞段长度仅为100,m，而工期却能够产生 1,d及以上的差距，可见各洞段中与其他洞段相比取值不同的施工参数对工期的影响较大，而根据上文分析可知，取值不同的施工参数有掘进速度、停机时间和衬砌时间 3个．故此 3个参数对工期的显著影响可以得到实例证明，同时也可说明进行输水隧洞施工工期敏感性分析对于工程施工的合理安排是有科学的指导意义．

表2 100 m洞段施工参数与工期Tab.2 100 m-tunnel construction parameters and duration

5 结 论

本文针对输水隧洞 TBM 施工过程中工期的不确定性现象，对引起工期不确定性的关联因素和不确定性因素进行了多因素综合敏感性分析，基于全局综合敏感性分析法的正交试验设计分析了因素主效应和耦合效应对工期不确定性的影响，并运用该方法对工程实例进行了分析．

(1) 分两个阶段进行了工序工期对总工期不确定性影响、参数对工序工期不确定性影响的主效应分析，可以有效识别出施工过程中需要重点控制的关键工序和关键机械参数．

(2) 对比引起工序工期不确定性和引起总工期不确定的施工参数，揭示参数主效应对工期不确定性影响的一般规律，为施工参数的选取提供科学依据．

(3) 在主效应分析结果的基础上，进行参数耦合效应对工期不确定性影响的分析，确定对工期不确定性影响最大的参数组合，从而在对关键施工参数进行重点控制的基础上，进一步合理化施工机械之间的搭配组合，使施工组织计划得到再次优化．

以往将针对工期不确定性现象进行的分析研究应用于输水隧洞 TBM 施工组织管理时，决策者无法依据定量数据和全局综合性分析结果制定合理的施工组织计划，本文研究克服了这一问题，为输水隧洞TBM施工过程的合理优化提供了科学依据．

［1］ Bi Lei，Ren Bingyu，Zhong Denghua，et al. Real-time construction schedule analysis of long-distance diversion tunnels based on lithological predictions using a Markov process[J]. Journal of Construction Engineering and Management，2014，4(1)：1-16.

［2］ 钟登华，刘奎建，杨晓刚. 施工进度计划柔性网络仿真的不确定性研究[J]. 系统工程理论与实践，2005，2(4)：107-112.Zhong Denghua，Liu Kuijian，Yang Xiaogang. Uncertainty analysis for construction scheduling with flexible network simulation[J]. Systems Engineering—Theory &Practice，2005，2(4)：107-112(in Chinese).

［3］ 钟登华，宋海良，王 帅. 基于三维地质模型的TBM施工动态可视化仿真[J]. 系统仿真学报，2008，20(6)：5548-5552.Zhong Denghua，Song Hailiang，Wang Shuai. Dynamic visual simulation of TBM construction based on 3-D geological model[J]. Journal of System Simulation，2008，20(6)：5548-5552(in Chinese).

［4］ 刘奎建. 大型地下洞室群施工进度实时控制研究[D].天津：天津大学建筑工程学院，2007.Liu Jiankui. Real-Time Control for Construction Scheduling of Large Scale Underground Structure Group[D].Tianjin：School of Civil Engineering，Tianjin University，2007(in Chinese).

［5］ 黄培志. 引水隧洞 TBM 施工风险分析理论方法与应用[D]. 天津：天津大学建筑工程学院，2009.Huang Peizhi. Risk Analysis Theory of Diversion Tunnel TBM Construction and Its Application[D]. Tianjin：School of Civil Engineering，Tianjin University，2009(in Chinese).

［6］ 刘东海，黄培志. 隧洞 TBM 施工过程柔性循环网络建模与仿真分析[J]. 土木工程学报，2010，10(6)：115-121.Liu Donghai，Huang Peizhi. Flexible cyclic operation network modeling and simulation analysis of TBM construction process[J]. China Civil Engineering Journal，2010，10(6)：115-121(in Chinese).

［7］ 刘东海，黄培志. 基于熵权的隧洞 TBM 施工进度风险分析[J]. 中国农村水利水电，2010，12(4)：110-112.Liu Donghai，Huang Peizhi. An analysis of TBM construction schedule risk based on entropy weight[J].China Rural Water and Hydropower，2010，12(4)：110-112(in Chinese).

［8］ 温 森，赵延喜，杨圣奇. 基于Monte Carlo-BP神经网络 TBM 掘进速度预测[J]. 岩土力学，2009，30(10)：3127-3132.Wen Sen，Zhao Yanxi，Yang Shengqi. Prediction on penetration rate of TBM based on Monte Carlo-BP neural network[J]. Rock and Soil Mechanics，2009，30(10)：3127-3132(in Chinese).

［9］ 赵延喜，徐卫亚. 基于 AHP和模糊综合评判的 TBM施工风险评估[J]. 岩土力学，2009，30(3)：793-798.Zhao Yanxi，Xu Weiya. Risk assessment of TBM construction for tunnels based on AHP and fuzzy synthetic evaluation[J]. Rock and Soil Mechanics，2009，30(3)：793-798(in Chinese).

［10］ Chung T H，Mohamed Y，AbouRizk S. Bayesian updating application into simulation in the north edmonton sanitary trunk tunnel project[J]. Journal of Construction Engineering and Management，2006，132(8)：882-894.

［11］ Pennington T W，French R，Cook R F，et al. Borehole GPR to detect and map deviated H-pile foundations[J].American Society of Civil Engineers，2007，13(2)：1-11.

［12］ AbouRizk S. Role of simulation in construction engineering and management[J]. Journal of Construction Engineering and Management，2010，136(10)：1140-1153.

［13］ Pennington T W，Richards D P. Understanding uncertainty：Assessment and management of geotechnical risk in tunnel construction[J]. Geo-Risk，2011，29(8)：552-559.

［14］ You Xiaomin，Tonon F. Event tree and fault tree analysis in tunneling with imprecise probabilities[J]. GeoCongress，2012，29(1)：2885-2894.

［15］ Serra J B，Mirand L. Ground uncertainty implications in the application of the observational method to underground works：Comparative examples[J]. Foundation Engineering in the Face of Uncertainty，2013，12(3)：254-270.

［16］ Zhang Sherong，Du Chengbo，Sa Wenqi，et al. Bayesian-based hybrid simulation approach to project completion forecasting for underground construction[J]. American Society of Civil Engineers，2013，21(9)：1-9.

［17］ Touran A，Toshiyuki A. Simulation of tunneling operations[J]. Journal of Construction Engineering and Management，1987，113(4)：554-568.

［18］ 束龙仓，朱元生. 地下水资源评价中的不确定性因素分析[J]. 水文地质工程地质，2000，6(1)：6-8.Shu Longcang，Zhu Yuansheng. Uncertainties in the analysis of groundwater resource evaluation[J]. Hydrogeology & Engineering Geology，2000，6(1)：6-8(in Chinese).

［19］ 肖 峻，耿 芳，杜柏均，等. 基于关联规则的城市电力负荷预测模型智能推荐[J]. 天津大学学报，2010，43(12)：1079-1085.Xiao Jun，Geng Fang，Du Bojun，et al. Intelligent recommendation of urban power load forecasting models based on association rules[J]. Journal of Tianjin University，2010，43(12)：1079-1085(in Chinese).

［20］ 罗立哲，胡志根，刘 全，等. 土石围堰边坡稳定的多因素综合风险分析[J]. 天津大学学报：自然科学与工程技术版，2013，46(7)：617-622.Luo Lizhe，Hu Zhigen，Liu Quan，et al. Comprehensive risk analysis of rock-fill cofferdam slope stability considering multiple random factors [J]. Journal of Tianjin University：Science and Technology，2013，46(7)：617-622(in Chinese).

［21］ 方开泰，马长兴. 正交与均匀试验设计[M]. 北京：科学出版社，2001.Fang Kaitai，Ma Changxing. Orthogonal and Uniform Design[M]. Beijing：Science Press，2001(in Chinese).

［22］ 刘瑞江，张业旺，闻崇炜，等. 正交试验设计和分析方法研究[J]. 实验技术与管理，2010，13(9)：52-55.Liu Ruijiang，Zhang Yewang，Wen Chongwei，et al.Study on the design and analysis methods of orthogonal experiment[J]. Experimental Technology and Management，2010，13(9)：52-55(in Chinese).

［23］ 钟登华，李景茹，刘奎建. 全过程动态仿真技术及其在大型工程施工管理中的应用[J]. 天津大学学报，2003，36(3)：347-352.Zhong Denghua，Li Jingru，Liu Kuijian. Dynamic simulation technology for whole construction processes and its application to large-scale construction project [J].Journal of Tianjin University，2003，36(3)：347-352(in Chinese).

［24］ 褚春超，郑丕谔，王德东. 复杂工序关系的模糊网络计划分析与建模[J]. 天津大学学报，2006，39(5)：631-636.Chu Chunchao，Zheng Pi’e，Wang Dedong. Analysis and modeling of fuzzy network planning considering complicated activity relationship[J]. Journal of Tianjin University，2006，39(5)：631-636(in Chinese).

［25］ 钟登华，刘东海. 大型地下洞室群施工系统仿真理论方法与应用[M]. 北京：中国水利水电出版社，2003.Zhong Denghua，Liu Donghai. Research on System Simulation Theory and Application for Construction Processes of Large-Scale Underground Structure Group[M]. Beijing：China Water Power Press，2003(in Chinese).