基于旋转及尺度空间拓展的图像修复算法

何 凯，郑 欢，张丽莹

(天津大学电子信息工程学院，天津 300072)

数字图像修复技术是计算机视觉领域的重要研究课题，其主要研究内容在于如何利用图像中的已知信息对破损区域进行填充，最终保证修复图像的效果自然合理．该技术在字幕、污点、划痕去除、老照片修复、影视特技、文物保护等领域都具有重要的意义和研究价值．

数字图像修复的经典算法是 Criminisi等[1]于2003年提出的基于样本块的修复算法，该算法利用置信度函数和结构性函数来确定修复的优先权函数，可实现大区域破损纹理图像的自动修复．

传统基于样本块的修复算法在修复图像结构时容易出现块效应和误匹配．针对这一问题，国内外学者提出了一些改进方法．Wexler等[2]提出利用迭代算法来优化能量函数，通过下采样形成多级金字塔图像，分别对每层金字塔图像进行块搜索和填充，改善了整体修复效果．Bugeau等[3]提出将纹理合成、几何偏微分方程以及邻域像素一致性综合为一个能量函数，通过最小化该能量函数完成修复过程，取得了较好的修复效果．谢伙生等[4]提出了一种基于样本块的优化方法，在考虑置信度和数据项的同时，增加了是否接近原始边界因素的影响，改善了修复效果. Kwok等[5]将图像转换到频域进行处理，通过选择少数频域系数来评估匹配情况，并将梯度引入到填充破损区域的过程当中，为图像匹配提供了新的思路．何凯等[6]在传统图像修复算法优先权系数的基础上，增加了方向性优先权系数，为纹理合成时各点的传播方向和进度提供索引，能够有效克服传统纹理合成方法没有考虑方向性的缺点．

在结构优化方面，Zhang等[7]提出将块稀疏度优先权和动态结构标签裁剪综合成一个全局优化模型，保证了纹理和结构修复效果的正确性．李志丹等[8]根据块结构稀疏度值来选择不同大小的样本块及邻域一致性约束，以自适应获得稀疏表示的指导信息．还有一些学者提出利用结构曲线来改善结构修复效果．Sun等[9]提出利用人机交互方案来解决图像结构的修复问题，通过人为干预，手动添加匹配块的搜索范围，提高了结构图像修复质量和速度．Pan等[10]采用自然图像局部自相似的假设，将显著结构曲线由已知区域拓展到破损区域，能够较好地修复破损区域内部的结构曲线．

除此之外，利用离散马尔科夫随机场(MRF)模型来改进修复效果也是当前的一个研究方向，Komodakis等[11]和 Pritch等[12]分别利用置信度传播BP和图像分割的方法来优化 MRF模型，将块和像素位置进行重新分配，以改善图像修复效果．2012年，Sun等[13]使用图像中样本块及其最优匹配块的位移，利用分布最密集的k个位移为修复图像提供信息来源，并利用 MRF优化完成修复过程，提高了结构图像的修复效果．

传统基于样本块的图像修复及其改进方法存在一个缺陷，即只能在平移空间中进行搜索，当图像中出现旋转及尺度变换时，无法实现匹配块的最优选取．针对上述问题，本文通过改进能量函数来实现搜索空间的旋转和尺度空间拓展，并利用 LM(Levenberg-Marquadt)优化算法[14]求解最优变换系数，以实现旋转和尺度变换时最优匹配块的自动搜索．

1 Patchmatch快速搜索算法

Barnes等[15]提出了一种快速块匹配搜索算法Patchmatch，其最大特点是可以利用相邻块之间的相互关系来传播邻域信息．

1.1 随机初始化

针对图像 A的所有样本块，定义其在图像 B中的匹配矢量函数为

即以图 A中某样本块的中心点像素坐标a作为该样本块的块坐标，该样本块在图像 B中的匹配块坐标为 b．

初始化过程对A中所有块在B中随机分配一个匹配块，然后进行传播和随机搜索，通过迭代优化来更新匹配块．

1.2 传 播

在奇数次迭代时，利用已知的 m ( x - 1,y)和m ( x,y -1)矢量来更新 m ( x,y)，以向右侧和下方传播有效信息；设 D (v)表示A中位于(x,y)的块和B中位于(x,y)+v的块的最小均方误差，则 m ( x,y)更新为

偶数次迭代时可向左侧和上方传播信息，此时选用 ( 1,)x y+m 和 (, 1)xy+m 作为候选匹配矢量．

1.3 随机搜索

假定(',')xy是A中块坐标为(,)xy的样本块在B中当前分配的块坐标，定义搜索半径为

式中：w为样本块的最大搜索半径；{α|0 ＜ α＜1}为搜索半径转换比率；1 ＜ Ri+1＜ w ．当 i＝0，1，2，…时，在以点(x',y ') 为中心、Ri+1为半径的范围内随机选取候选块对当前匹配块进行优化更新．

2 本文算法

设图像破损区域为 T，信息来源区域为 S，所有和破损区域相交的样本块称为目标块，其余称为信息块；则图像修复的目的就是从源区域S中寻找最优区域块，并将其填充到破损区域 T当中．本文采用Patchmatch搜索算法对所有目标块进行最优匹配块的全局搜索．传统能量函数[2]的表达式为

其中

式中：tn、sxn分别表示以点n为中心的目标块和以点xn为中心的信息块；ip为块内部像素的相对索引；D 为两个块像素值的最小均方误差．

2.1 能量函数的改进

传统能量函数只能针对平移空间进行搜索，当图像包含其他变换信息时无法实现样本块的准确搜索．为此，本文将传统能量函数加以改进，增加了旋转和尺度变换参数，以实现变换空间的拓展；同时加入了梯度项以减小匹配误差．拓展后的能量函数可表示为

式中：第 1项为目标块 tn和变换后的信息块 f (sxn)在R、G、B三维像素值的最小均方误差；∇为水平和垂直方向的梯度；∇tn为目标块tn的梯度值；f(∇sxn)为对信息块 sxn的梯度值进行变换；λ为加权系数，表示梯度的影响权重；f为变换函数； f(sxn)为以 xn为中心的信息块 sxn进行旋转和尺度变换之后彩色通道的像素值．将 f (sxn)定义为

式中 fxn(ip)为对点 xn为中心的信息块进行变换后在图像中的绝对索引． fxn(ip)的定义为

式中：Rθn为进行θn角度旋转后的块内相对索引；αn为尺度变换系数(将样本块的中心点作为旋转和尺度变换的中心点). 式(7)中 f(∇ sxn)的计算方法与f(sxn)类似．

针对尺度变换，采用正方形搜索块，对旋转变换采用正方形内切圆作为搜索块，顺时针旋转θn后的块内相对索引 Rθnip依照式(10)、(11)确定，即

式中0xi、0yi 和xi、yi分别为旋转前后的二维相对索引．

2.2 利用LM算法获取最优化模型参数

以确定旋转变换的最优参数θ为例，设随机初始化步奏分配的当前最优匹配块是nxs，ˆ()fθ=t为nxs旋转θ角度后对目标块nt的估计．给定初始角度0θ和目标块nt，误差函数定义为

本文利用 LM 迭代算法寻找使得平方误差(ε( θ ) )Tε ( θ )达到最小时的最优旋转角度θ．每次迭代都寻找新的δθ，使其满足

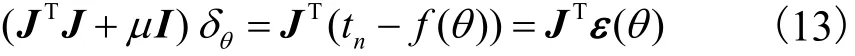
式中：J是雅克比矩阵 ∂ f（θ） / ∂θ；μ＞0；I为单位矩阵．若由式(13)获得的δθ满足关系

则更新 θ =θ+δθ，同时减小μ；否则增加μ并重新求解式(13)，直到求得的δθ满足式(14)，更新θ= θ +δθ.

依照上述法则不断求解式(13)，设初始点为θ0，通过迭代产生一系列 θ1、θ2、…，直到收敛到局部最优解．

调整μ的目的在于确保式(14)成立．当算法满足以下条件之一时停止迭代，并取当前θ为最优旋转参数．

(1)式(13)右边项 JTε低于某个阈值ε1；

(2)θ的相对变化量δθ低于某个阈值ε2；

(3)误差项 (ε (θ) )Tε (θ)低于某阈值ε3；

(4)迭代次数达到最大值 kmax．

具体做法如下．

(1)角度方面．将角度范围均匀分成 8个区间，设当前分配的最优匹配块的角度参数为θ，则以角度θ为起点，在360°范围内依次增加(或减小)45°，作为LM迭代的起始角度，在以每个迭代起始角度为中心的±22.5°范围内，通过迭代计算各自的最优参数．

(2) 尺度方面．设搜索块大小为ω，当前分配的最优匹配块的尺度参数为 {α0|1 ≤ α0≤2}，将尺度范围[ω ,2ω]均匀分成8等份，以尺度α0ω为起点，依次增加(或减小)ω8，作为迭代尺度参数的起始值，在以每个迭代起始尺度参数为中心的±ω 16的范围内进行迭代，获得最优尺度参数．

最后，利用具有最小平方误差 (ε ( θ ) )Tε( θ )的最优系数对当前最优匹配块进行变换，以去除旋转和尺度变换的影响．

2.3 算法流程

首先对破损图像进行下采样，构造高斯金字塔图像，从金字塔顶层开始，逐层对图像迭代进行块搜索和信息填充[2]．算法流程如图1所示，其中，k表示当前金字塔层数，2n表示当前层已迭代次数，1n和N分别表示在第k层、第2n次迭代时，空间拓展及LM优化块搜索过程的已迭代次数和所需的总迭代次数．

图1 本文算法流程Fig.1 Flow chart of the algorithm proposed in this paper

3 实验结果及分析

为了验证本文方法的有效性，选取了4幅具有尺度和旋转变化的图像进行实验仿真，如图2～图5所示．其中图(a)代表原始图像，图中的小线框内部代表破损区域．

本文实验均采用5级高斯金字塔，由粗到细进行迭代，以在保证准确度的前提下降低计算量．其中第5级进行15次迭代，以后每级迭代次数递减3次，每次迭代的总迭代次数 N设为 100；除此之外，能量函数的梯度项设置至关重要，如果不设置梯度项或者其权重系数过小，会造成图像在结构变化处出现模糊和平滑，丢失结构信息；反之，如果权重系数过大，则会导致纹理信息的误匹配，根据实验仿真结果，本文能量函数的梯度权重设为λ＝0.2，样本块大小选为11，LM参数选取为 ε1=ε2=ε3=1×10-4，kmax＝10，随机搜索过程取w为图像的最大维度，α＝0.5．

从图 2和图 3中可以看出，破损区域 T内的图像信息与源区域 S中相应图像具有明显的尺度变换特征，由于传统全局优化算法不具有尺度变换的功能，无法准确找到最优样本块，修复效果较差；而本文方法通过尺度拓展，并利用LM优化算法确定尺度最优化系数，可以显著提高匹配的准确度，有效地解决了这一问题，取得了理想的修复效果．

图2 五角星尺度图像修复效果Fig.2 Result of five-pointed star scale image

图3 热气球尺度图像修复效果Fig.3 Result of fire balloon scale image

图4 中破损区域T与源区域S之间存在明显的旋转变换关系．从图 4的修复结果对比中可以明显看出，传统方法在解决这一类问题时效果明显不够理想；而本文方法不仅可以有效地修复圆盘的弧形边界，而且在相对复杂的花纹图盘方面，修复效果也更为准确．同理，对于图 5齿轮中的破损部分，由于本文方法有效地利用了旋转信息，将最优旋转角度作用于匹配块，从而有效地降低了匹配误差，取得了理想的修复效果；而传统 Criminisi样本块修复算法和space-time修复算法由于缺乏相应的旋转变换能力，修复后图像具有明显的人工修复痕迹．

图4 圆盘旋转图像修复效果Fig.4 Result of disk rotation image

图5 齿轮旋转图像修复效果Fig.5 Result of gear rotation image

4 结 语

本文提出了一种基于旋转及尺度变换的图像修复算法，通过改写能量函数并利用LM优化方法求得最优变换参数，当图像存在旋转及尺度空间变换时，能够明显提高块匹配的准确度，取得了比较理想的修复效果．

［1］ Criminisi A，Perez P，Toyama K. Object removal by exemplar-based inpainting [C]// Proceedings of 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Wisconsin，USA，2003：721-728.

［2］ Wexler Y，Shechtman E，Irani M. Space-time completion of video[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2007，29(3)：463-476.

［3］ Bugeau A，Bertalmío M，Caselles V，et al. A comprehensive framework for image inpainting [J]. IEEE Transactions on Image Processing，2010，19(10)：2634-2645.

［4］ 谢伙生，潘姣君. 基于纹理合成的图像修复优化方法[J]. 福州大学学报：自然科学版，2013，41(3)：305-310.Xie Huosheng，Pan Jiaojun. Optimal method of image inpainting based on texture synthesis [J]. Journal of Fuzhou University：Natural Science Edition，2013，41(3)：305-310(in Chinese).

［5］ Kwok T H，Sheung H，Wang C C L. Fast query for exemplar-based image completion[J]. IEEE Transactions on Image Processing，2010，19(12)：3106-3115.

［6］ 何 凯，焦青兰，孟春芝，等. 非均匀纹理图像大区域修复算法[J]. 天津大学学报，2012，45(4)：314-318.He Kai，Jiao Qinglan，Meng Chunzhi，et al. Nonregular texture image completion algorithm in large region[J]. Journal of Tianjin University，2012，45(4)：314-318(in Chinese).

［7］ Zhang X，Liu B. Image completion with patch sparsitybased global optimization[C]// IEEE 2011 3rd International Conference on Computer Research and Development(ICCRD). Shanghai，China，2011：62-66.

［8］ 李志丹，和红杰，尹忠科，等. 基于块结构稀疏度的自适应图像修复算法[J]. 电子学报，2013，41(3)：549-554.Li Zhidan，He Hongjie，Yin Zhongke，et al. Adaptive image inpainting algorithm based on patch structure sparsity[J]. Acta Electronica Sinica，2013，41(3)：549-554(in Chinese).

［9］ Sun J，Yuan L，Jia J，et al. Image completion with structure propagation [J]. ACM Transactions on Graphics，2005，24(3)：861-868.

［10］ Pan P，Zheng X，Xu Q，et al. Image completion with automatic structure propagation [C] // IEEE 2012 8th International Conference on Computational Intelligence and Security (CIS). Guangzhou，China，2012：305-309.

［11］ Komodakis N，Tziritas G. Image completion using efficient belief propagation via priority scheduling and dynamic pruning [J]. IEEE Transactions on Image Processing，2007，16(11)：2649-2661.

［12］ Pritch Y，Kav-Venaki E，Peleg S. Shift-map image editing [C]// IEEE 2009 12th International Conference on Computer Vision. Kyoto，Japan，2009：151-158.

［13］ He K，Sun J. Statistics of patch offsets for image completion [C]// Computer Vision-ECCV 2012. Springer Berlin Heidelberg，2012：16-29.

［14］ Madsen K，Nielsen H B，Tingleff O. Methods for Non-Linear Least Squares Problems [M]. Copenhagen，Denmark：Technical University of Denmark，2004.

［15］ Barnes C，Shechtman E，Finkelstein A，et al. Patch-Match：A randomized correspondence algorithm for structural image editing [J]. ACM Transactions on Graphics，2009，28(3)：24-33.