TFR模型下关于几何分布产品加速寿命试验的Bayes分析
2015-07-18金莹
金 莹
(河南财经政法大学 统计学院,河南 郑州 450002)
TFR模型下关于几何分布产品加速寿命试验的Bayes分析
金 莹
(河南财经政法大学 统计学院,河南 郑州 450002)
讨论了TFR模型下几何分布参数的Bayes估计,通过实例对加约束与不加约束的两种估计结果进行对比.
几何分布; TFR模型; Bayes估计
0 引言
许多产品(如开关等)的寿命就可以用几何分布来描述.由于其无记忆性的优点,常用于可靠性理论的研究中.随着科技的发展,许多产品的寿命大幅增加,若想快速得到产品寿命数据,就需要进行加速寿命试验.本文讨论的TFR模型下关于几何分布产品加速寿命试验的Bayes推断.
将一批产品从t=0时刻开始置于应力水平S1下做试验,试验到时刻t1将未失效产品置于应力水平S2(S2>S1)下继续做试验,且试验到产品都失效为止.假定应力水平S1的失效率函数为λ1(x),应力水平升高后,S2水平下的失效率函数δλ1(x)δ(δ>1).设上述条件下加速寿命试验的寿命时间X*的失效率函数为λ*(x),则λ*(x)表示为:
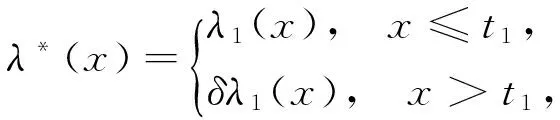
其中δ可能和t1有关,记为δ(t1),并称其为损伤因子.这种加速损伤模型称为损伤失效率(TFR)模型[1].
TFR模型可推广到一般的k步步加试验[2].在k步步进应力水S(t)=Si,
ti-1 设G(p)表示参数为p的几何分布,X表示几何分布产品的寿命,X~G(p)即 P(X=k)=pqk,k=1,2,…,(q=1-p). 则 P(xi>km)=P(xi≥km+1)=(1-p)k1(1-δ1p)k2-k1(1-δ2p)k3-k2…(1-δm-2p)km-1-km-2(1-δm-1p)km-km-1. 在应力S1下,产品失效率λ1(k1) 定理1[3]若产品在恒定应力S1下产品服从参数为p的几何分布,那么在TFR下,在恒定应力S2(>S1)下产品的寿命仍服从几何分布,只是改变了参数而已.即当k1→0时, P(X=k)=limk1→0[δ(k1)p(1-p)k1(1-δ(k1)p)k-k1-1]=δ(0)p(1-δ(0)p)k-1. 由定理1可知,产品寿命在恒定应力S2下仍服从几何分布,参数为δ(0)p. 则其在截尾场合下似然函数为: 因为 所以得到如下约束条件 取p的先验密度函数为 因为没有相关信息,所以取δ1,δ2,…,δm-1的先验密度函数为均匀分布 … 其中 其中 所以p,δs(s-1,2,…,m-1)有约束条件的Bayes估计为: 沿用记号,已知无约束条件 其中 所以p,δs(s-1,2,…,m-1)有约束条件的Bayes估计为: 例1 将20个几何分布产品进行试验,在应力S1下有3个产品失效(寿命为26,152,153),继续试验至k1=200 次提高应力至S2,有5个产品失效(寿命为247,282,289,344,348)继续做试验至k2=350次提高应力至S3,有1个产品失效(寿命为 445),继续试验至k3=450次提高应力至S4,至再有6个产品失效停止试验(寿命为463,488,507,535,536,549),未失效产品数r5=5.另外参数真值为p=7.686×10-4,δ1=2,δ2=6,δ3=24. 参数的Bayes估计为: 例2 将20个几何分布产品进行试验,在应力S1下有3个产品失效 (寿命为5,67,84),在继续试验至k1=200次提高应力至S2,有6个产品失效(寿命为215,222,255,288,303,339),续做试验至k2=350次提高应力至S3,有2个产品失效(寿命为355,373),继续试验k3=450次提高应力至S4,至再有1个产品失效停止试验(寿命为 547),而未失效产品个数r5=5.另外参数真值为p=7.686×10-4,δ1=2,δ2=3,δ3=4. 参数的Bayes估计为: 从两个例子可以看出参数p加约束的估计比不加约束的估计更接近真值.当3个损伤因子的δi,i=1,2,3真实值比较接近时,不加约束的估计就可能出现逆序的情况.总之,一般情况下加约束的和不加约束的估计两种方法都是适用的,加约束的比不加约束的估计更接近真值. [1]Bhattacharyya G K,Soejoeti Z A. A Tampered Failure Rate Model for Step-Stress Accelerated Life Test[J]. Communications in Statistics-Theory and Method,1989,18(5):1627-1643. [2]Madi M T. Multiple Step-Stress Accelerated Life Test:The Tampered Failure Rate Model[J]. Communications in Statistics-Theory and Method,1993,22(9):2631-2639. [3]徐晓岭.几何分布和 Weibull分布产品的统计分析[D].上海:上海师范大学,2004. [4]金莹,张立. 几何分布定时截尾简单恒加试验的最优设计[J].新乡学院学报:自然科学版,2008,25(2):16-18. [5]徐晓岭,王蓉华,朱崇恺. 全样本场合几何分布产品步进应力加速寿命试验TFR模型下的统计分析[J].强度与环境,2005,32(4):46-52. [责任编辑:李春红] TheBayesianAnalysisforGeometricDistributionBasedonTamperedFailureRateModelUnderStep-StressAcceleratedLifeTesting JIN Ying (School of Statistical Institute,Henan University of Economics and Law,Zhengzhou Henan 450002,China) Geometric distribution is one of the most important discrete life distributions. The Bayesian estimation for geometric distribution parameter based on TFR Model are discussed,it was compared cthe estimation under restraint condition with the estimation of no restraint condition by using the examples. geometric distribution; TFR model; bayesian estimation 2015-06-05 河南省教育厅人文社会科学基金项目(2014GH556) 金莹(1980-),女,河南新乡人,讲师,硕士,研究方向为数理统计、经济统计. E-mail:jinying7788@yeah.net O212.6 :A :1671-6876(2015)03-0214-061 多步步加试验截尾场合下加约束的Bayes估计

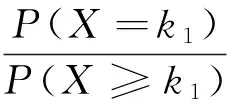




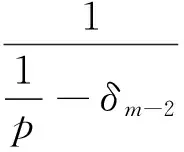
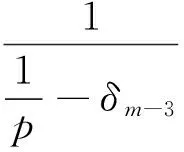
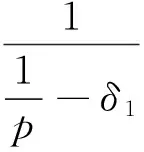
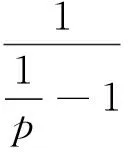
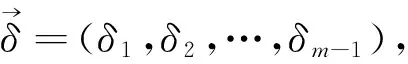
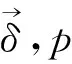
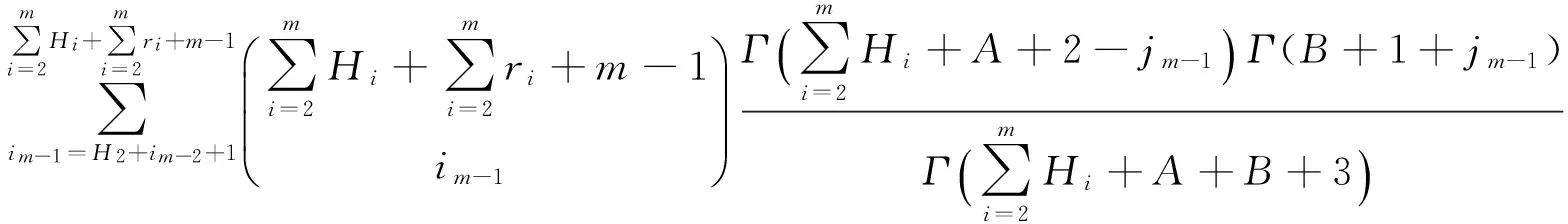
2 多步步加试验截尾场合下未加约束的Bayes估计

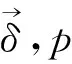
3 实例分析


