时滞的功能反应的食饵捕食模型的稳定性

戴志伟,戴志梅

(1.兰州交通大学 数理学院,甘肃 兰州 730070; 2.宁德师范学院 数学系,福建 宁德 352000)

时滞的功能反应的食饵捕食模型的稳定性

戴志伟1,戴志梅2

(1.兰州交通大学 数理学院,甘肃 兰州 730070; 2.宁德师范学院 数学系,福建 宁德 352000)

利用Ruan S的关于时滞的功能反应的食饵捕食模型的稳定性判定方法的思想，研究了时滞的功能反应的食饵模型及其稳定性.

时滞； 功能反应； 食饵捕食模型； 稳定性

0 引言及预备知识

文章介绍了时滞和功能反应的食饵捕食模型,引入判定该模型的方法和相关定理[1].种群动力学作为生物数学的重要分支近年来得到了充分的重视,捕食者与食饵之间的动力学行为一直是一项重要的研究领域,不同类型的食饵捕食模型已经得到了广泛的研究和长足的发展.因此不论从生物学家还是从数学家的角度来说研究捕食者与食饵的动力学都有深远的影响[3,5-8].本文主要介绍关于非单调的功能效应的时滞食饵捕食系统,系统如下:

其中x(t),y(t)分别表示食饵和捕食者的样本的密度,r表示在没有捕食者的情况下,食饵的成长率,K表示环境对食饵的容纳量,D表示捕食者的死亡率,A表示捕食者和食饵保持半饱和稳定下功能反应已经达到半个极大值时的捕食者的半稳定常量,H表示捕食者的收获率常量,τ表示时滞,它们都是大于零的常量.

本文主要研究该模型的稳定性,主要思路： 1)有正平衡点的情况下求出正平衡点; 2)对该方程系统进行线性化,得到相应的线性系统; 3)应用常微分方程理论求出相应的特征方程和特征根,判断根的实部是否是负的;有负实部,则该系统的正平衡点稳定,否则不稳定,同时有可能在相应的分岔点会产生霍普夫分岔[2-4].

1 主要结论

本部分主要研究如下系统的稳定性情况

(1)

其中x(t),y(t)分别表示食饵和捕食者的样本的密度,r表示在没有捕食者的情况下,食饵的成长率,K表示环境对食饵的容纳量,D表示捕食者的死亡率,A表示捕食者和食饵保持半饱和稳定下功能反应已经达到半个极大值时的捕食者的半稳定常量,H表示捕食者的收获率常量,τ表示时滞,它们都是大于零的常量.

(I)求出正平衡点

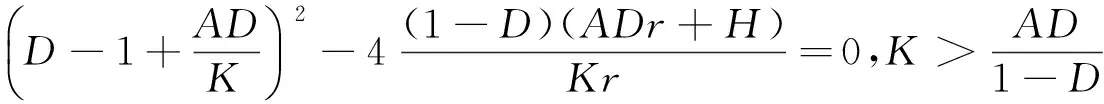
(II)线性化

令z1(t)=x(t)-x0,z2(t)=y(t)-y0,得到如下形式

其中

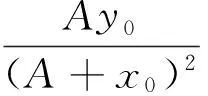
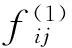
则线性系统如下:

(2)

λ2-(α1e-λτ+β2)λ+β2α1e-λτ-α2β1=0

(3)

当τ变化时,有些特征值的实部是否随着增大趋于零或者有可能由负变为零,甚至最后成为正的情况.因此,可以假设iω是式(3)的根,则带入式(3)整理得

ω2+α2β1=α1[β2cos(τω)-ωsin(τω)]

(4)

-β2ω=α1[β2sin(τω)+ωcos(τω)]

(5)

由式(4)的平方加上式(5)的平方,得

(6)

(III)稳定性

(A)当τ=0时,特征方程为λ2-(α1+β2)λ+β2α1-α2β1=0,则(H1)α1+β2<0.(H2)β2α1-α2β1>0,

(B)当τ≠0时，

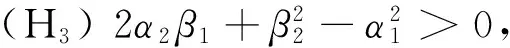
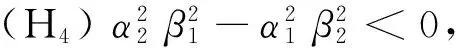
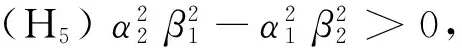
(C)稳定性情况如下:

如果(H1),(H2)和(H3)成立时,式(6)的根对所有τ≥0,都有负实部,那么系统(1)的正平衡点(x0,y0)是渐近稳定的;

由式(6)可得

由式(4)乘以β2加上式(5)乘以ω,得

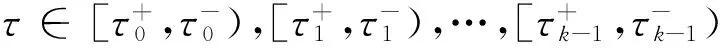
由式(4)×β2+式(5)×ω,得

如果(H1),(H2)和(H3)成立时,式(6)的根对所有τ≥0,都有负实部,那么系统(1)的正平衡点(x0,y0)是渐近稳定的;

[1]Ruan S. On Nonlinear Dynamic of Predator-Prey Models with Discrete Delay[J].Quart Appl Math,2009,4(2):140-188.

[2]Wu J,Liu Z H,Yuan R,et al. The Effects of Harvesting and Time Delay on Predator-prey Systems with Holling-Type II Functional Re1[J].Siam Journal on Applied Mathematics,2013,70(4):1178-1200.

[3]Zhang G,Zhu L L,Chen Bosha. Hopf bifurcation in a delayed differential algebraic biological economic system[J].Nonlinear Analysis Real World Applications,2011,12(3):1708-1719.

[4]Zhang L,Wang H L,Hu H Y. Symbolic computation of normal form for Hopf bifurcation in a retarded functional differential equation with unknown parameters[J].Commun Nonlinear Sci Numer Simulat,2012,17(1):3328-3344.

[5]Simthe H. An introduction to Delay Differential Equations with Applicatins to the Life Sciences[M].The Federal Republic of Deutschland:Springer-Verlag,2011,87-166.

[6]Faria T,Magalhaes L T. Normal Forms for Retarded Functional Differential Equations and Applications to Bogdanov-Takens[J]. Differential Equations,1995(122):201-224.

[7]He X,Li C D,Huang T W,et al. Codimension two bifurcation in a simple delayed neuron model[J]. Neural Comput & Applic 2013,23(7):2295-2300.

[8]Dai G R,Xu C X. A predator-prey system with constant-rate prey harvesting under type-I functional response[J].Acta Mathematica Scientia,1994,14 (2):134-144.

[责任编辑：李春红]

TheStabilityofaDelayPredator-PreyModelwithFunctionalResponse

DAI Zhi-wei1,DAI Zhi-mei2

(1.School of Mathematics and Physics,University of Lanzhou Jiaotong,Lanzhou Gansu 730070,China)
(2.Department of Mathematics,Ningde Normal University,Ningde Fujian 352100,China)

In this paper,the stability of a delay predator-prey model with functional response was introduced; The methods of the main idea of S.Ruan for the stability of a delay predator-prey model with functional response is applied to this article,which is studied.

delay; functional response; predator-prey model; stability

2015-05-14

戴志伟(1989-),男,福建莆田人，硕士研究生,研究方向为科学与工程计算. E-mail:1026447889@qq.com

O175

:A

:1671-6876(2015)03-0210-04