滚动轴承振动速度的乏信息真值估计
2015-07-25栗永非时保吉
栗永非,时保吉
(新乡职业技术学院,河南 新乡 453006)
振动特性是滚动轴承的动态性能之一,对主机的动态性能、工作寿命及可靠性等有重大影响,其可以综合、全面反映轴承产品的整体质量水平[1-2]。为了从总体上把握轴承振动的基本特性,需要对轴承振动参数的真值进行评估。由于轴承振动特性具有乏信息特征,使得轴承振动特性的真值估计成为难题。目前,学者们已经研究了许多真值评估方法,如最大似然法[3-4]、最大后验估计[5-7]、加权平均法[8]和最小二乘逼近等[9],但这些通常都是基于大样本条件下进行的。为此,提出基于小样本的真值融合方法,该方法是对滚动平均法、隶属函数法、最大隶属度法、滚动自助法和算术平均法的多次融合。在此基础上,提出了乏信息条件下基于多个估计真值的融合方法的点估计,通过对圆锥滚子轴承的质量参数进行蒙特卡洛(Monte Carlo)模拟和试验研究,以验证文中所述融合方法的适应性和有效性。
1 真值融合模型
为解决乏信息系统的真值估计问题,采用多种数学方法进行研究,进而从多个侧面获取整个系统的属性信息。当方法不同时,评判准则各异,就会得到不同的属性信息。将获得的属性信息构成集合,就是所谓的估计真值集合。该集合从多个方面描述系统的属性特征,通过融合得到的属性信息,能更合理地对系统属性真值进行估计,即真值融合技术。
设系统输出的轴承质量数据序列为
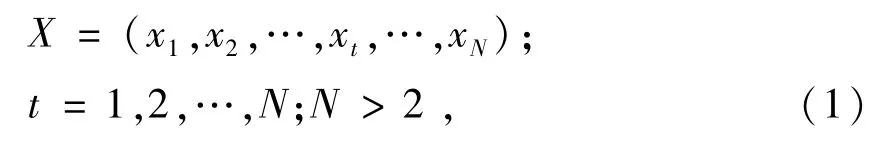
式中:xt为原始序列X中的第t个数据;N为数据的个数。
1.1 真值融合方法
由于研究的轴承质量数据序列概率分布未知且数据量很小,提出以下5种真值估计方法。
1.1.1滚动均值法
将(1)式中的数据由小到大排列,则
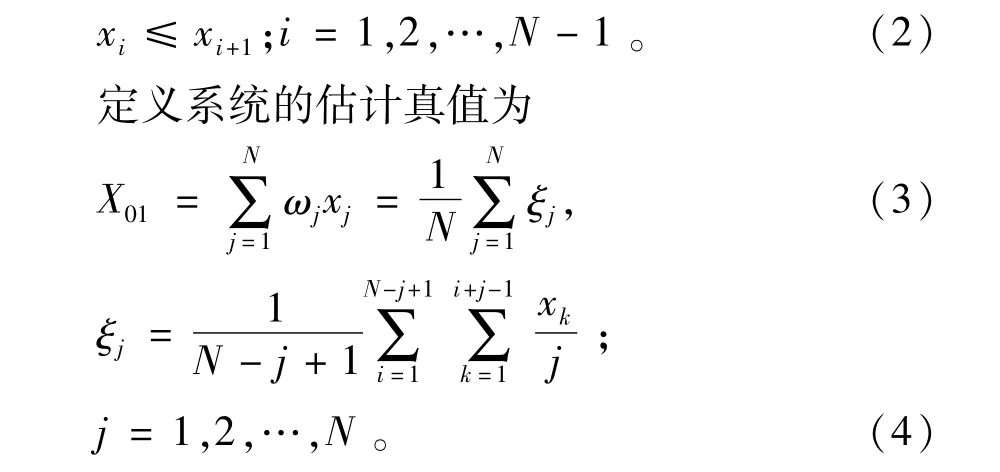
1.1.2 隶属函数法

作为一种定量融合方法,隶属函数法实际属于加权均值方法,权重即为隶属函数fi。
1.1.3 最大隶属度法
依据隶属函数法,设最大隶属度为


1.1.4 滚动自助法
设轴承质量数据序列X为
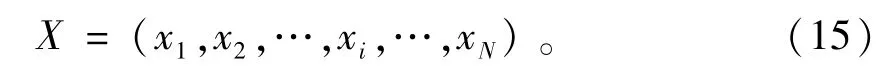
从序列X中进行自助抽样,等概率可放回地抽取mD=N个数据,则获得自助样本Xb,连续抽取B次,就能够得到B个自助样本

将自助样本从小到大排序,并分为Q组,就可以得到各组的组中值Xmq和概率密度函数f(x)或离散频率Fq,q=1,2,…,Q。
以频率Fq为权重,则估计真值为
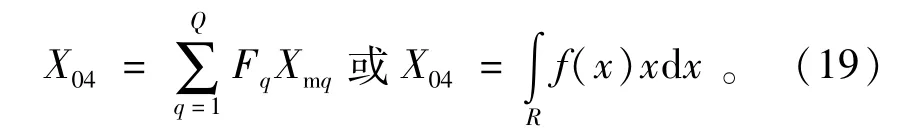
1.1.5 算术平均法
算术平均法是第5种真值估计方法,是最常用的点估计方法之一。
定义系统的估计真值为

1.2 估计真值的融合
采用多种数学方法得到估计真值的解集X0后,将X0作为第0次融合序列,表示为
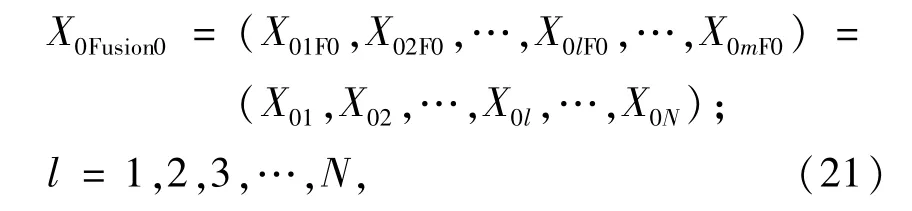
式中:X0l为采用第l种数学方法得到的真值的估计结果。
然后采用所提出的融合方法对X0Fusion0进行计算,得到第1次融合序列

式中:X0lF1为采用第l种数学方法对第0次融合序列融合的计算结果。
依此类推,第k次融合序列为
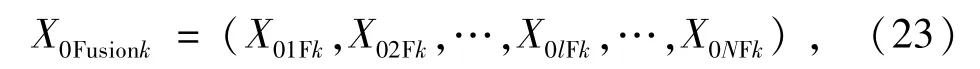
式中:X0lFk为对采用第l种数学方法对第k-1次融合序列融合的计算结果。
定义3:存在任意小的实数ε,若极差满足

式中:N为第k-1次融合序列融合计算结果的个数。此准则称为极差准则。
1.3 约定真值
根据误差理论和统计理论,如果差异很小,基于大样本的5个估计真值可以被认为是接近数学期望EM的,故可以被视为约定真值Xtrue,即
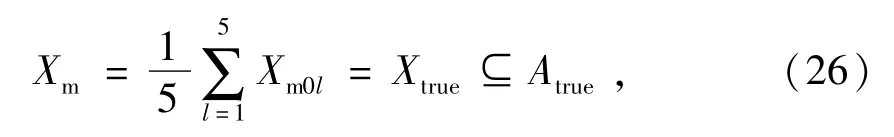
式中:Xm为5个真值的平均值;Xtrue为约定真值;Atrue为系统属性的真值集合。
2 试验研究
试验对象为30204圆锥滚子轴承,随机抽取30套轴承,利用B1010振动仪采集轴承径向振动速度信号(包括低频、中频和高频)。图1所示为轴承振动数据序列。需进行5个测试系列的试验研究,其中每个测试序列有30个数据。
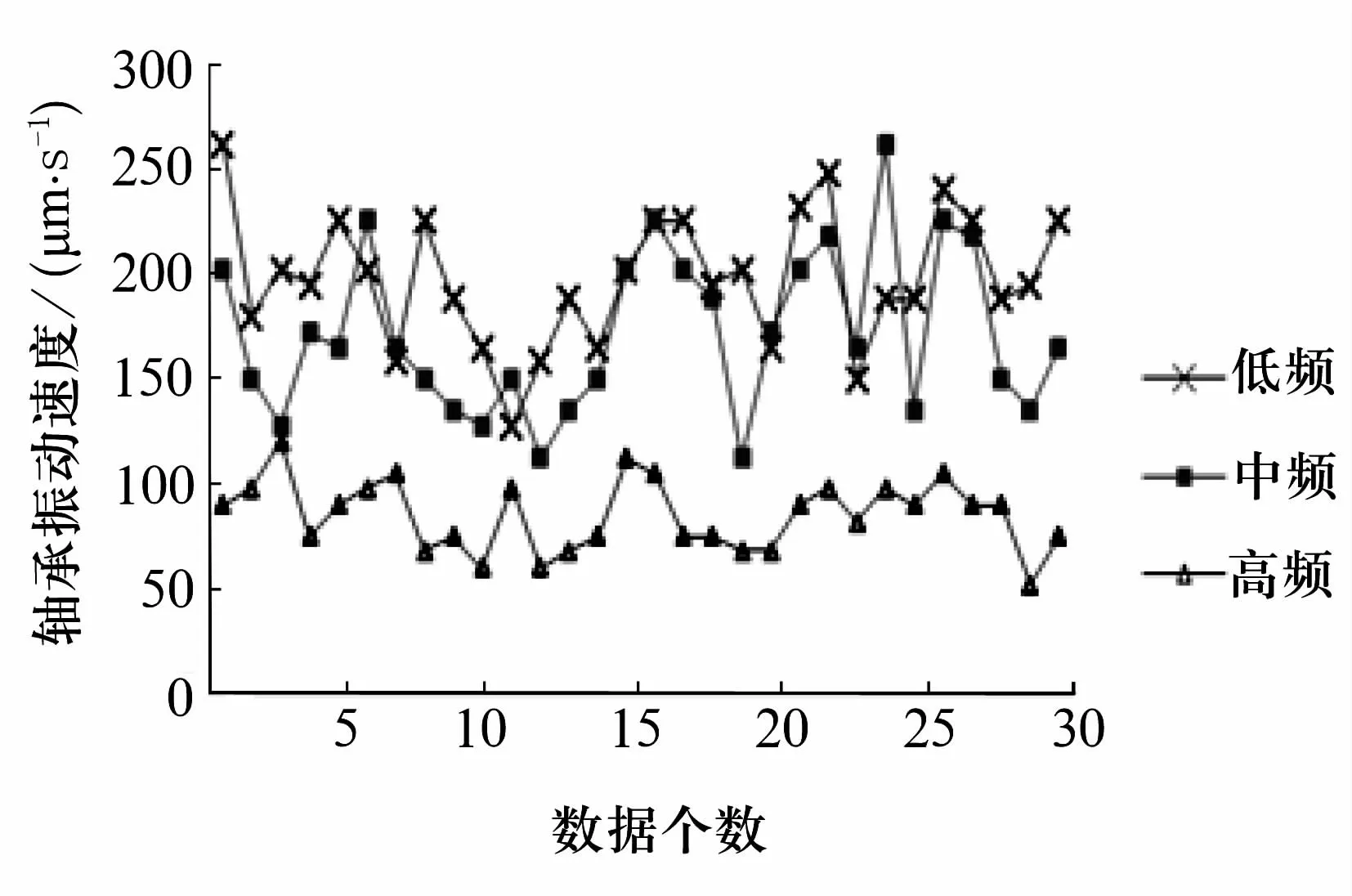
图1 轴承振动数据序列
2.1 大样本条件下的约定真值
如上所述,平均值Xm可用于描述大样本条件下的约定真值Xtrue。在此基础上,将30个数据作为测试样本,即Ntest=30,则分别采用5种真值融合方法计算出5个估计真值,结果见表1。
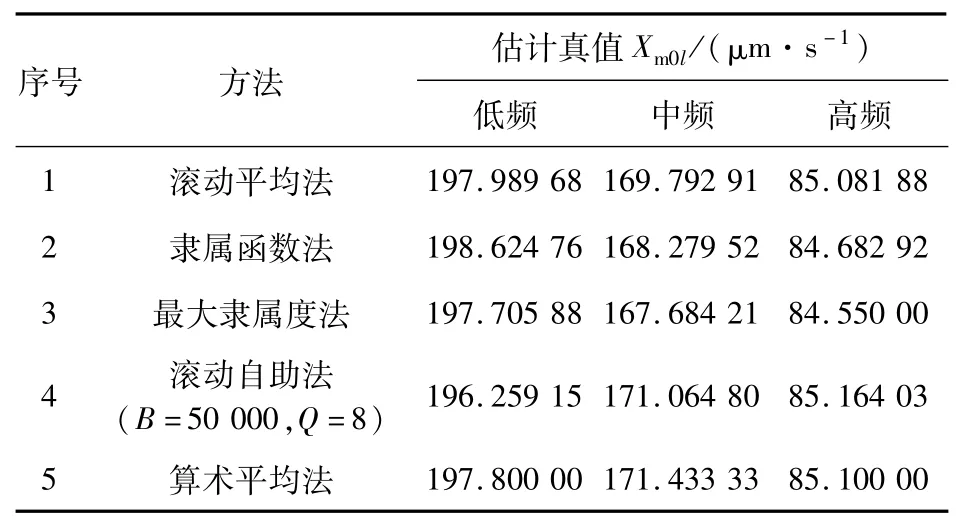
表1 轴承振动速度在大样本N test=30下的估计真值
由表1可知,在大样本条件下轴承低频、中频和高频速度的5个估计真值差别均很小,最大相对误差分别为1.2%,2.2%和0.7%,则5个估计真值的平均值即为低、中、高频振动速度的约定真值Xtrue,即低频XmL=197.7μm/s=XLtrue,中频XmM=169.7μm/s=XMtrue,高频XmH=84.9 μm/s=XHtrue。
2.2 小样本条件下轴承振动速度的评估
从图1中分别选取低、中、高频振动速度测试序列的前5个数据,即小样本个数N=5,形成新的测试序列X,
低频XL=(262,180,202,195,225),
中频XM=(202,150,128,172,165),
高频XH=(90,98,120,75,90)。
采用上述5种融合方法,基于小样本的轴承振动速度估计真值及与约定真值的相对误差见表2。
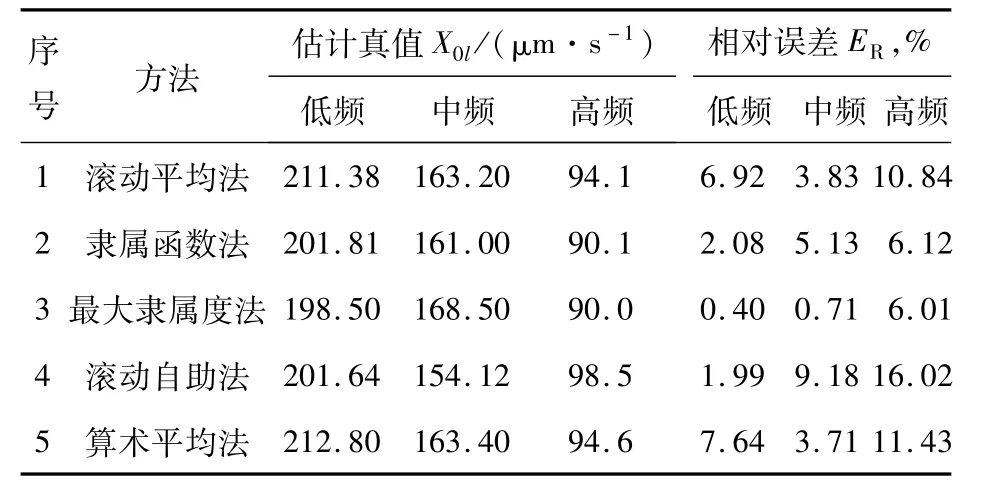
表2 小样本条件下振动速度的估计真值(N=5)
从表2可以看出,在小样本条件下,这5种方法得到的估计真值有明显不同,与约定真值的相对误差也很大。
根据误差理论对有效数据的控制原理,分别采用滚动平均法、隶属函数法、最大隶属度法、滚动自助法和算术平均法对对低频、中频和高频振动估计真值进行3次融合,结果见表3。
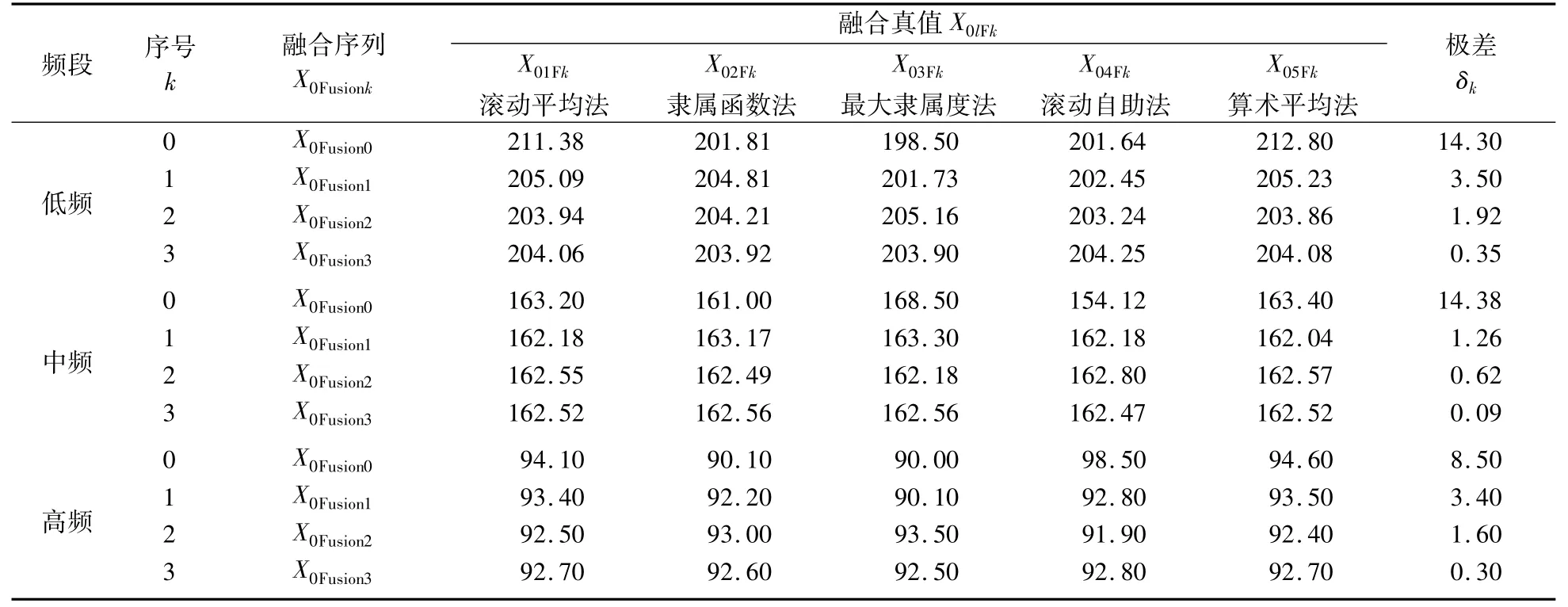
表3 轴承振动速度的估计真值的融合序列(N=5)
取ω=0.5,根据极限准则,最终估计真值见表4。
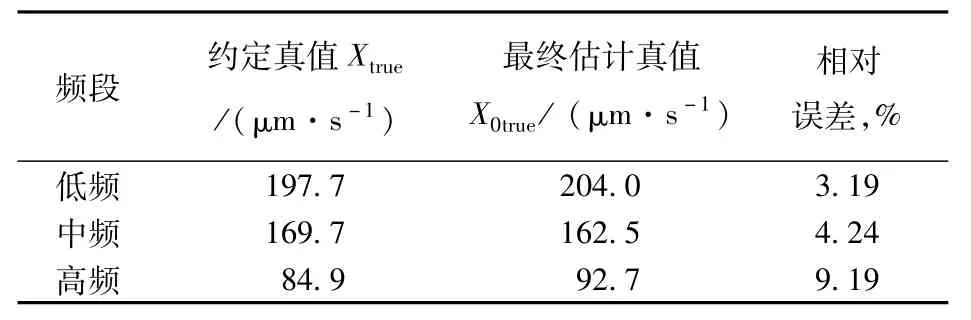
表4 小样本条件下的最终估计真值(N=5)
3 Monte Carlo仿真
采用Monte Carlo法模拟任意概率分布(本文为均匀分布)的随机过程,区间为[0,1],则得到随机过程的测试序列Xtrue(图2),测试序列数据个数为Ntest=1 024。显然,测试序列服从均匀分布。根据统计理论,均匀分布的数学期望为0.5,则测试序列的约定真值为U=0.5μm/s。
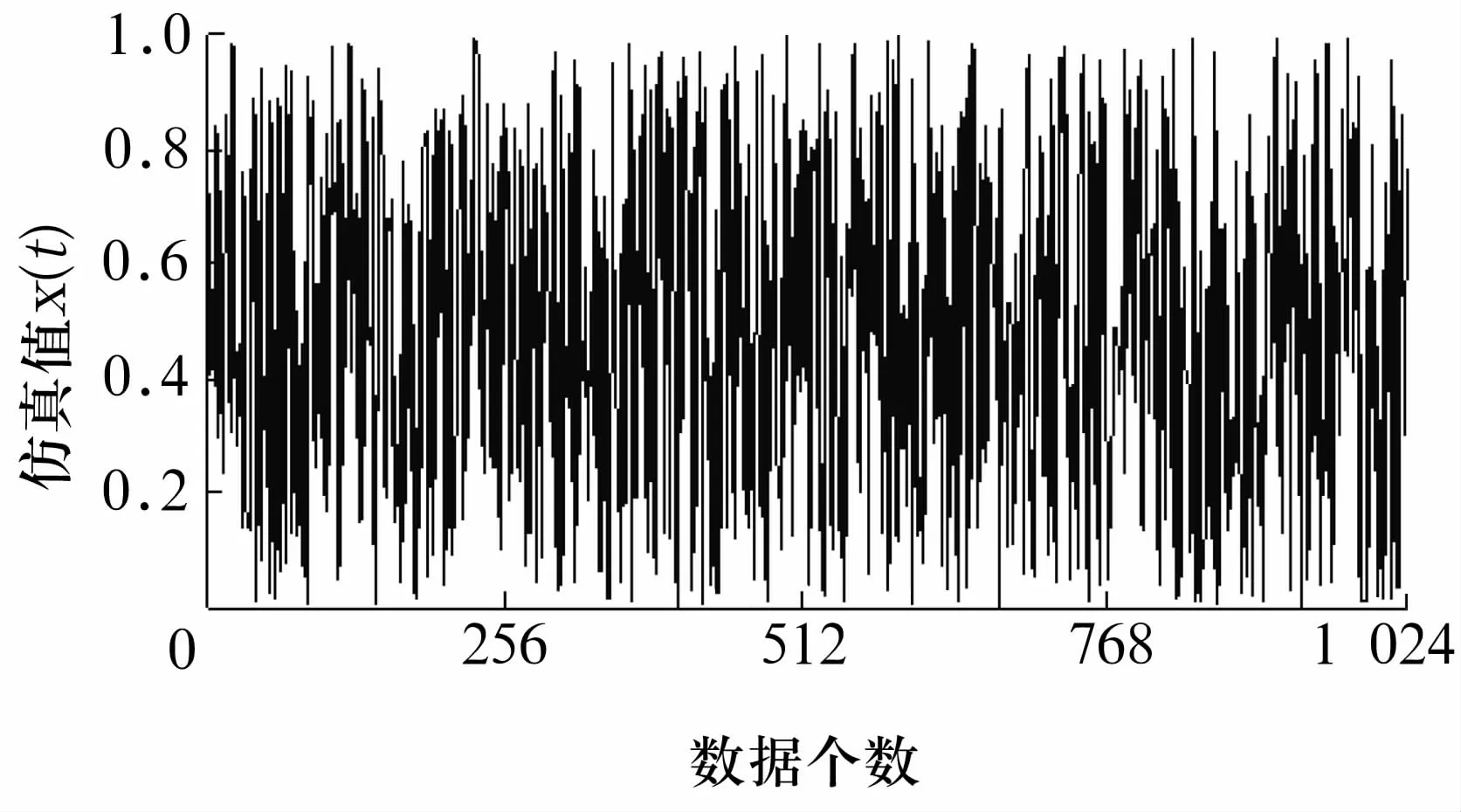
图2 基于Monte Carlo仿真的均布测试序列(N test=1 024)
从图1中选取测试序列的前5个数据,即小样本个数N=5,形成新的测试序列X=(0.773 74,0.406 97,0.724 49,0.557 77,0.387 96)。
采用上述方法,基于小样本的Monte Carlo仿真均布估计真值见表5。从表5很容易看出,这5种方法得到的估计真值明显不同,其与约定真值U的最大相对误差为20.51%,最小相对误差为10.62%。
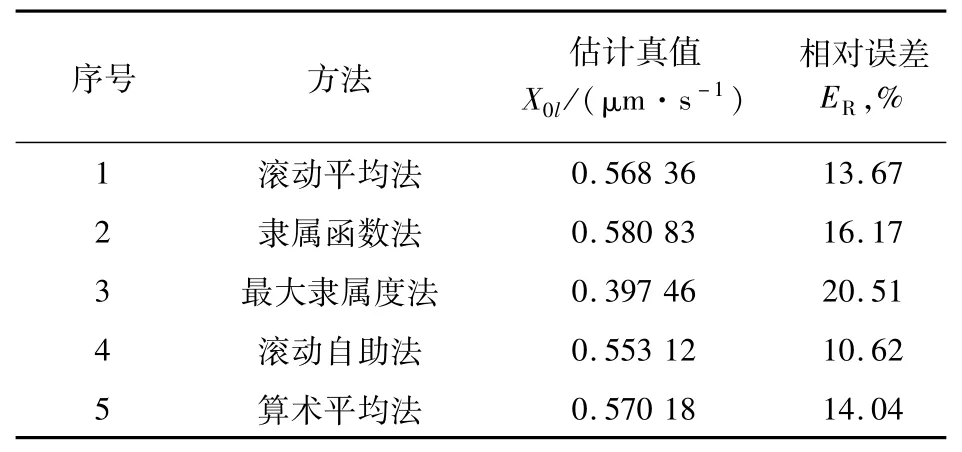
表5 基于小样本的均布估计真值(N=5)
对均布估计真值进行融合,结果见表6,取ε=0.005,根据极限准则,最终估计真值为
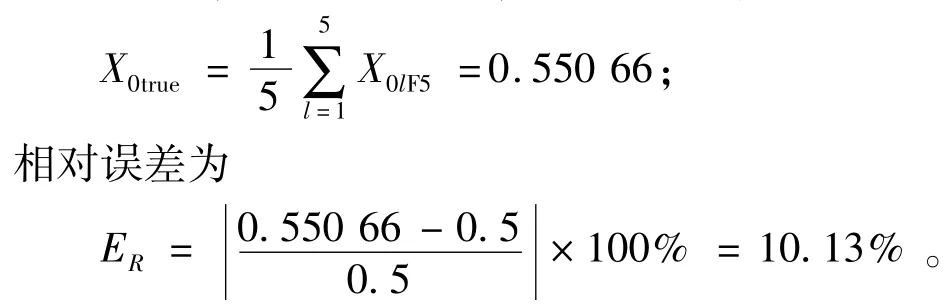
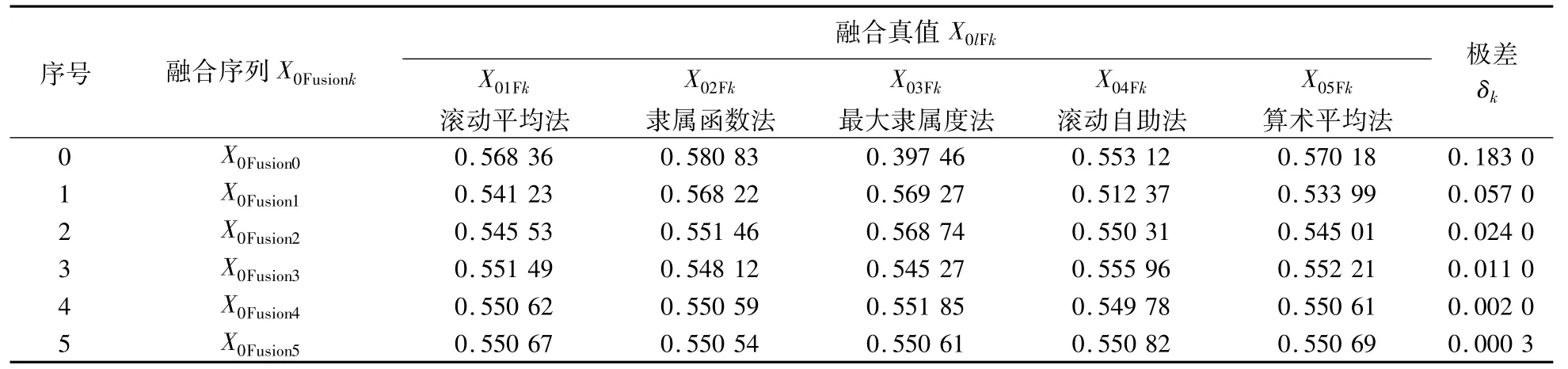
表6 均匀分布估计真值的融合序列
为便于观察,将这4个测试序列最后的结果总结于表7中,由表可知,在小样本条件下,传统估计真值和最终估计真值的相对误差范围为3.19%~10.13%。采用融合方法进行多次融合后,最大相对误差为10.13%,而采用单一方法的最大误差则达20.51%。
4 结束语
建立了真值融合模型,并通过圆锥滚子轴承振动试验研究证明,基于小样本的真值融合模型具有更高的评估精度,最大相对误差仅有9.19%,误差较小;而采用单一方法得到的最大相对误差通常较大。
通过Monte Carlo仿真进一步证明了真值融合模型评估的有效性,真值融合方法对于解决小样本和概率分布未知的问题具有可靠的估计结果。
