《数形结合思想》学习工具制作综述

展学林

特色与亮点

学习工具《数形结合思想》的最大特色是动态性，能在变动状态下保持对象之间不变的几何关系。而且涉及的所有图像全部是计算所得，而不是手工绘制，保证了准确性。《数形结合思想》涉及图形的旋转、切割、函数图像的动态交点、移动同时翻转等。

1.页面直观且管理灵活

学习工具最底端是一级菜单，直观形象。另外，可根据课堂需要与学生的水平进行跳跃式自由选择。

2.可即时无限次重复

课堂教学，学生学习层次不同，需要教师分层次教学。传统教学，不可能实现，因为教师面对的是全体学生，不可能各个兼顾，再次重复时间也不允许，尤其是一些步骤很长的讲解，如画图等。而本学习工具可以很轻松地进行重复讲解。在讲解过程中，可以根据需要按“Alt+[、Alt+]”来加速或减速，以配合教学和学习进度。

3.节省了时间

数学课上与图像有关的内容大都是浪费时间而且也不够准确。传统教学课堂容量大大受限，而利用本学习工具，既准确地描绘了图形的特点，也可以在短时间完成操作，效果良好。另外，学生可以利用本学习工具自主学习、探索、再思考，以达到课堂上所不能实现的效果。

4.化抽象为形象，让运动过程一目了然

数学上的平移、旋转、切割等，只能是教师表达出来的“直观”，而学生根本没有看到这个图的运动变化过程，尤其不能全面把握图像的形成转变过程。本学习工具在这些方面做了改进。学生完全可以自己动手解决学习中的疑惑与困难，整个过程没有“盲区”。

5.便于学生自学，利于教师授课

本学习工具能够激发学生自主探讨学习的积极性。让学生不再机械地接受教师的说教，而变成主动地学习，由“要我学”变成“我要学”。当然，本学习工具也给教师的授课提供了便利。可谓教、学皆宜。

制作背景

数形结合思想，将代数式的准确与图像的直观有机地整合到一起，教师使用几何画板，使静态的图形变为动态，抽象的概念变得形象，枯燥的内容变得有趣，使课堂教学生动起来。利用几何画板，可以展示知识发生、发展的过程，更好地提示知识之间的联系。

本节课所选的所有例题均为课堂上曾经讲过的内容，在传统的课堂模式下，讲解只是限于讲解开头，展示结果，中间过程就这样被“忽悠”过去了。尤其是一些图像的运动过程，更是无从谈起，无法展现。因为中间过程是一个抽象的过程，不易表达，更无法显示。这一点一直是很多学生的“死穴”。也是很多教师的无奈。多年来，我一直想解决这一问题。信息技术的介入，使得这一过程变得容易多了。

教学内容分析与教学策略

《数形结合思想》是高三数学的复习专题。主要介绍数形结合法在不同领域的应用及联系。

在选择题目上，为了体现数形结合思想的广泛应用，我选择了一道平面解析几何例题，一道平面几何例题，两道函数例题，三道立体几何例题，另外，还有三道函数方面的练习题，以巩固所学方法，彰显学以致用的要旨。同时也让学生切身体会到方法的重要性。到了高三，绝对不是再简单地重复复习，而是把原本看上去风马牛不相及的内容进行有机整合，把原本一个个原孤立的点，联系到一起，形成一张知识网。

本学习工具在制作的时候选用数形结合思想，而没有选用数形结合法，主要是考虑到数形结合法有些狭隘，这样不利于高三复习，不利于开拓学生的思维，而数形结合思想便于学生领悟数形结合法在不同领域如立体几何、平面几何、平面解析几何、函数等方面的不同应用，使得数形结合思想的内涵更加丰富，真正体现了复习的主旨：复习并不是简单的重复，而是不同内容之间的有效整合。

设计思路及表现手法

《数形结合思想》这一节课是按授课习惯来设计，包括例题讲解、练习巩固、小结作业。整个过程符合教师的授课习惯和学生的认知规律。学习工具的设计分为一级菜单和二级菜单，按钮的功能全部写在按钮上，一目了然，所见即所得，哪怕一个新手也可以轻松操作。图1中最下面一行是一级菜单，而界面中的紫色文字部分（左侧部分）是二级菜单。根据需要也可以收起二级菜单，这样显得界面简单明了。

1.例题讲解，温故知新，一题多解，思维延伸

首先在课堂上简单复习数形结合思想的最初由来以及它的一些简单应用。再通过下面的例题讲解，体现数与形的真正结合，激发学生学习的兴趣与乐趣。下面逐一介绍。

（1）平面解析几何部分

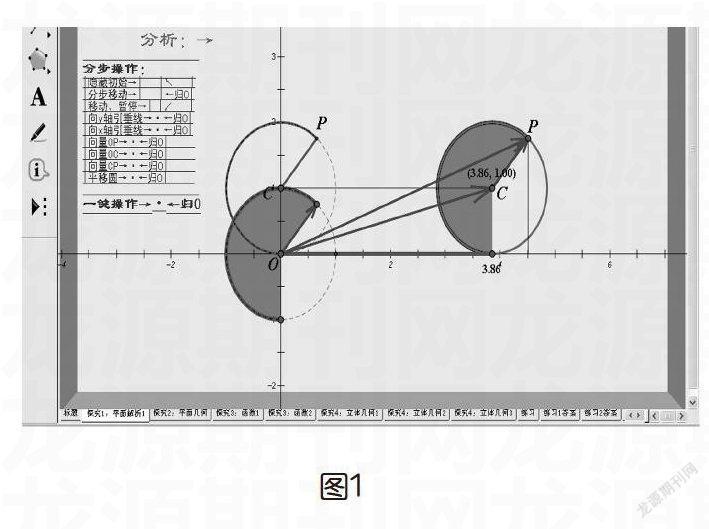
这是一道高考题，此题解法就是运用最简单的几何法，向x轴、y轴引垂线，这样，求出这两个线段的长即得P点横、纵坐标。其实这个解法过于普通，也体现不出不同知识点的相互联系。

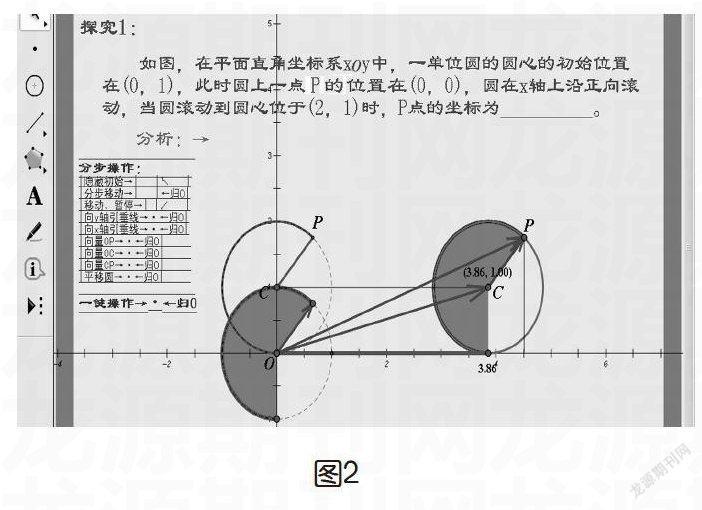
在讲解此题时，我讲解完上述方法之后，就给学生即时提了一个思考问题，如果让这个圆继续向右滚动，滚动到一个任意的位置，如图2中的位置C（3.86，1），此时学生会发现，原先方法虽然可用，但是费时。“那么有没有更好的解决办法呢？”这样一个不经意的提问，引导学生进入了另一个思考的空间，拓展了学生的思维空间，使得原本可以结束的思考再度被启动。

讨论之后，学生迫切希望能得一种更新的方法。这时候，教师适时插入一句：“求P点的坐标就是向量的坐标，而向量会随着P点的移动一直在变怎么办？”

在此过程中，学生会不断发现“新大陆”，激发了兴趣，也培养了他们的观察力及创新力。整个课堂气氛活跃而不滞怠，环环相扣，有序进行。

最终，教师点明方法：变化过程中，如果不变得越多，变化就越小，可以本着这个原则，利用，将 这个变量转变成一个常量和另一个变量，而这个变量可以平移到原点，利用平面向量、三角函数的知识来进行解决。

在这个过程中，我们不得不说，原本这道题目是一个平面解析几何，但是，经过延伸之后，就巧妙地把平面解析几何的问题转化为平面解析几何、平面向量、三角函数相结合、相联系的问题，一举数得，将连点成线，连线成网。

（2）平面几何部分

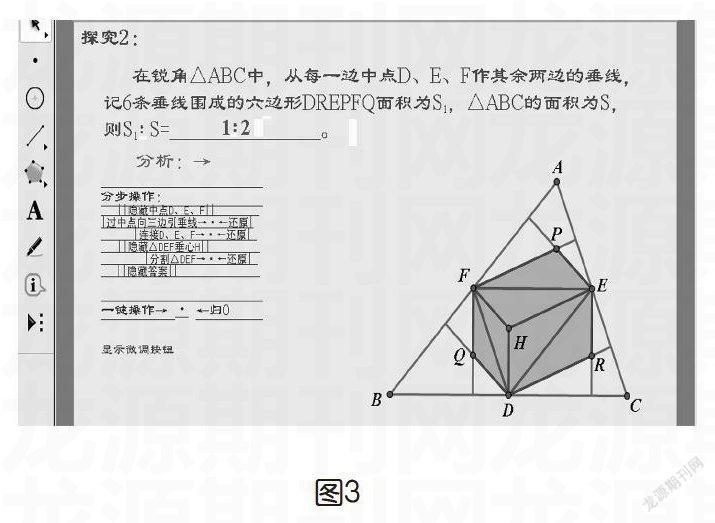
看到这个题目时（如图3），我们最容易想到的就是求出S1、S，这样就可以求出S1∶S。但是，本题纯粹利用了图形的分割，通过观察不得不说，数形结合思想应用得非常巧妙而精到。

由图像可知，此法形象直观，不做过多陈述。

（3）函数部分

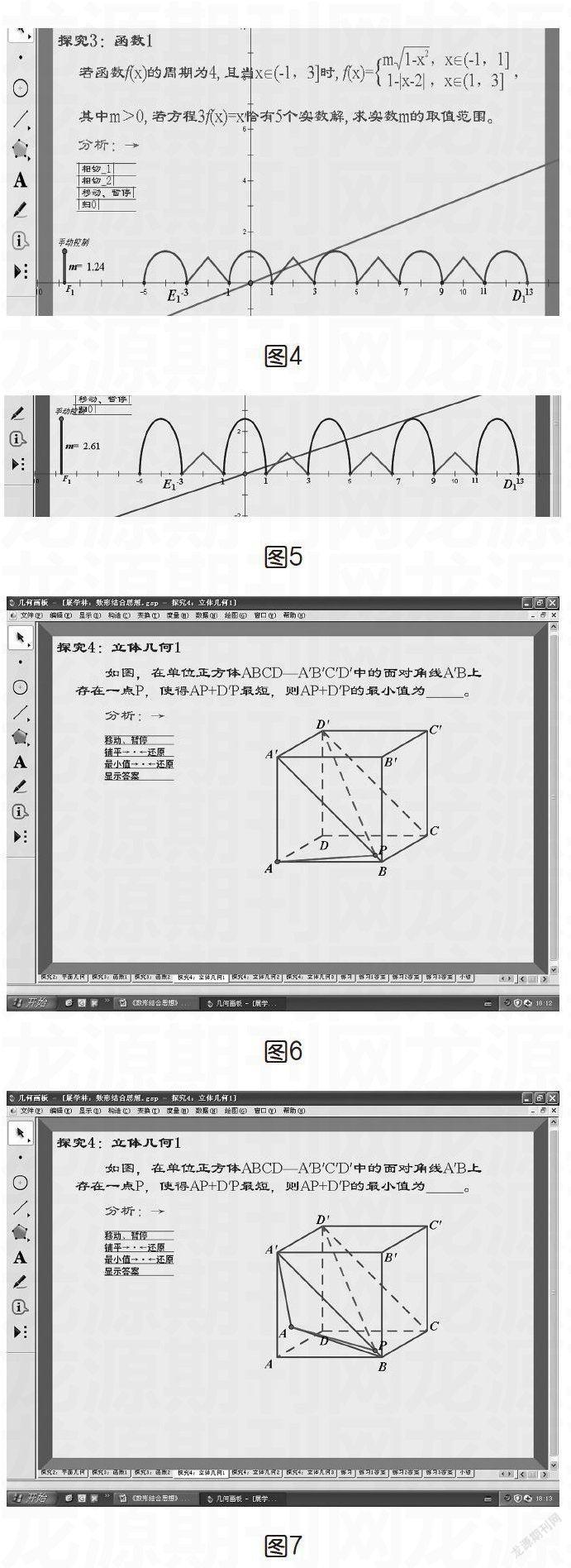
看到3f（x）=x这个公式（如图4），很容易让人想到要先化简，但是，首先f（x）是分段函数，其实，这是分段函数的第一段还含有一个参数m。

这样首先把3f（x）=x化成f（x）=，而求交点问题就转变成了求函数y=f（x）与y=的交点问题。而由于y=f（x）含有一个参数m，而m会影响图像，故而可以借助于函数的图像来研究交点问题，进一步可以观察m的变化如何影响函数y=f（x）的图像，这样就可以求出参数m的图像了。

如图4所示，当第一次相切时，恰好四个公共点。如图5所示，当第二次相切时，恰好五个公共点。而参数m的变化就会导致半个椭圆拉长还是缩短，故而由图像可知，求出参数m的取值范围。

（4）立体几何部分

本题是立体几何中的最小值问题（如图6），最常见的处理方式就是将一个弯曲或变折的平面铺平在一个平面上（如图7），根据两点间线段最短，求出折线段的和的最小值（如图8）。整个过程非常自然，学生看到整个演示过程，不再有任何疑问。

一个四棱锥五个面，一个四面体四个面，这两个几何体的所有棱长均相等，这样四面体的任何一个面都与四棱锥的侧面全等（如图9），这样当将它们平移（如图10），然后重叠之后（如图11），很容易这样考虑：5+4-2=7。但是，实际如何呢？我让学生根据本学习工具自己动手演示。

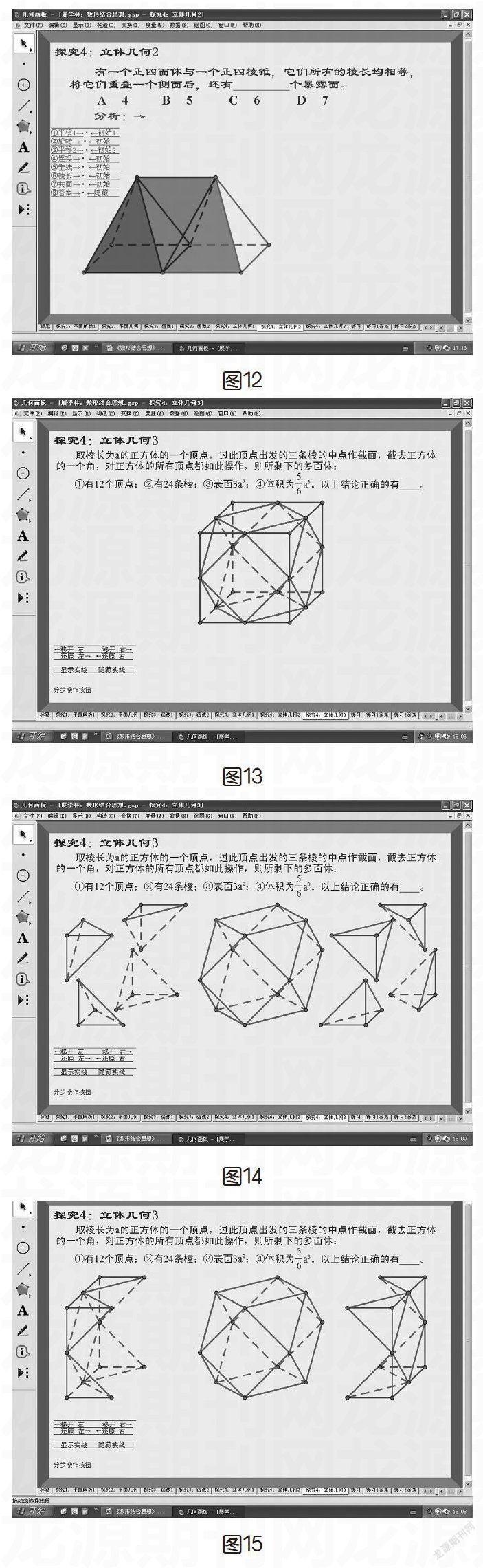
学生发现，先把原来的四棱锥向右平移一个，这样显然紫色的平面与红色的平面是在一个平面上（如图12），而中间空出的部分正好是正四面体的形状。根据图示可以发现紫色的平面与绿色的平面实际上是一个平面，这样最终形成的几何体就是5个平面。

看来数学不能只通过眼睛来学习，而要通过眼睛去观察、大脑去思考，全方位的联系才能真正找到答案。在这一过程中，学生的学习兴趣与信心倍增。将一个枯燥的学习过程，变得轻松自然。而且最为主要的是学生自己发现、探讨、解决问题，体现了教师为主导，学生为主体的思想。

教师在讲解这一几何问题时，在黑板上擦了画，画了擦，仅凭教师说，学生完全看不到切割之后的形状。学生根本想象不出，切割完后，到底是一个什么样的几何体。但是，本学习工具把整个切割过程完全展现在学生眼前，拟物性非常强。

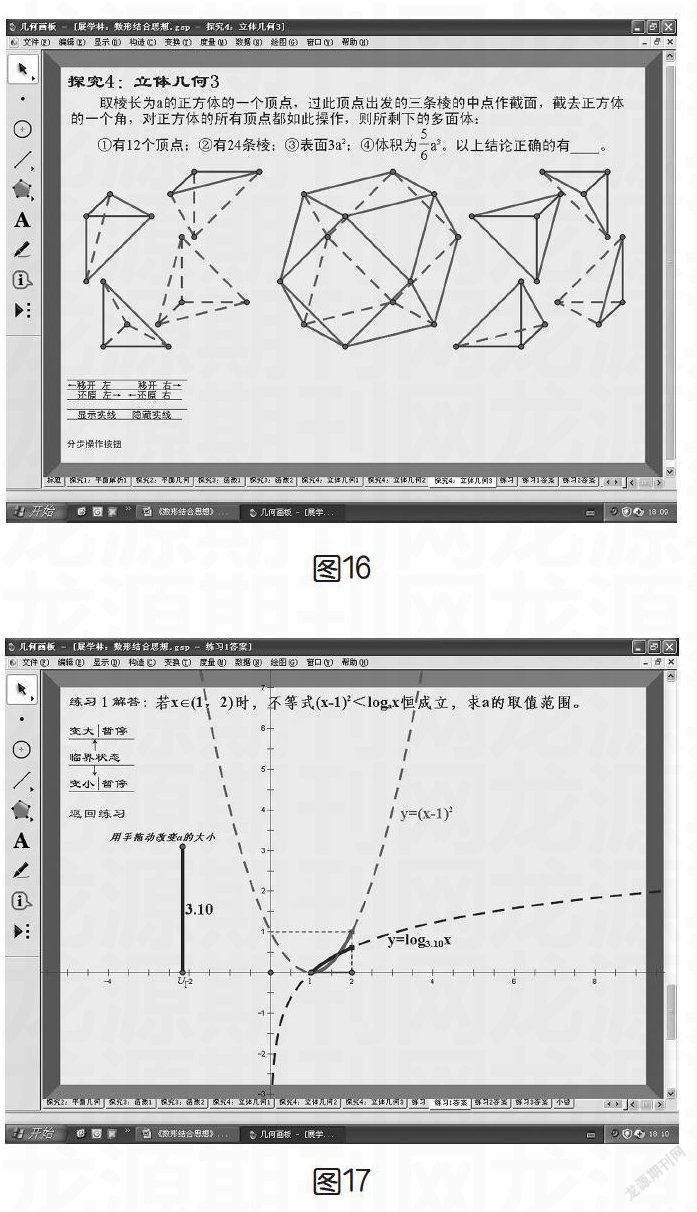
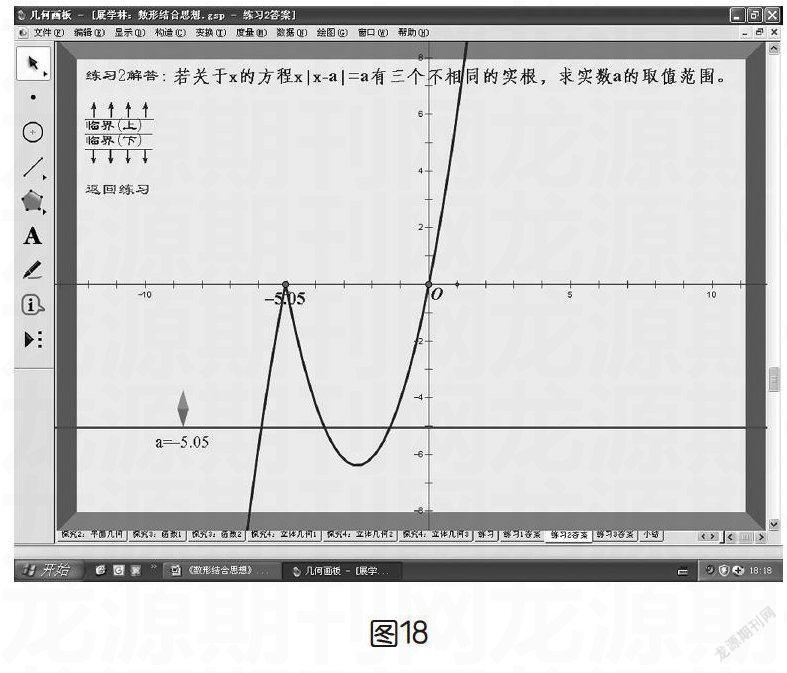
原先的几何体（如图13），移开左边的几何体（如图14），移开右边的几何体（如图15），左右两边的几何体手动调整，可以自由拖动（如图16）。这样，最终几何体的表面是什么样，就一清二楚了。

2.自主练习，巩固提高，举一反三，思维提升

练习的设计层层递进，让学生在不知不觉中突破了难点。整个过程跨度自然，由一个层级跃到另一个层级，而不是让学生感到遥不可及，也并不是随意而为，需要思考才能解决问题。思维量增大，学生的学习能力也随之提高。

本题所设计的题目，也是数形结合题型中的“熟面孔”，平常学生只能看到一些固定的程式，但用手拖动“用手拖动改变a的大小”，就可以轻松改变对数函数的底，进一步改变对数函数，这样这两个函数在区间（1，2）上的交点问题就一目了然了，在复习了对数函数的底数变化的同时，也完全可以看到对数函数因为底的变化而改变的过程。学生如果掌握熟练，可以自己点击按钮，如果嫌演示的速度太快，可以手动拖动，直观形象，就好像把这两个函数的图像“玩于股掌之间”（如图17）。

本题目的设置如果用代数法，非常麻烦，因为方程两边的式子中均含有参数a，而且不容易分离，这样，可以代数式与图像并举，让学生观察a的变化如何改变两边函数y=x|x-a|与y=a的位置关系，进一步明确如何改变它们的交点的问题（如图18）。

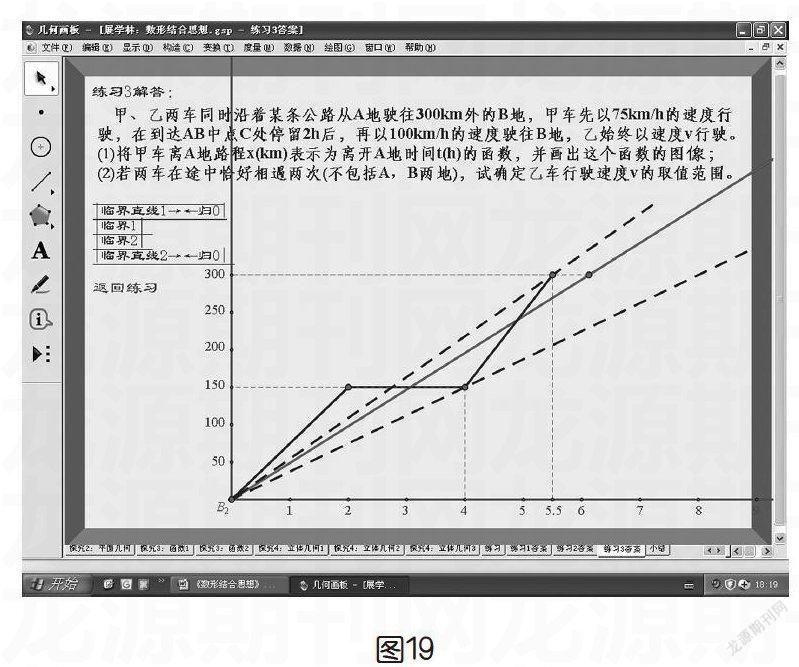
这是一个函数图像的交点问题。这样，我们就可以很轻松地看出它们的交点，问题迎刃而解（如图19）。

3.提纲挈领，汇总提升，浓缩精华，融会贯通

让学生快速掌握本节课的内容框架，可以让学生复述本节课学习重点内容，使学生能够全面掌握《数形结合思想》的精髓，为课余的复习、练习、巩固、提高做好了知识储备。

内容结构与艺术布局

《数形结合思想》这一节课，完全按照由浅入深、化抽象为具体的思路来进行。利用学习工具节省了大量时间。而且每一个页面都可以根据学生的掌握情况进行重复，使再现讲课过程等成为现实，真正实现了分层施教。

考虑到学生的基础情况、对知识的掌握情况等，学习工具在设计内容上非常灵活，根据课堂内容可以随意选择例题练习，而有些不必要讲或者来不及讲的内容可以直接不用显示。这样不会使整堂课有残缺感。学习工具在制作时也充分考虑了色彩对学生的影响，背影颜色柔和大气，图形颜色也是清晰醒目，调动了学生的多种感官。

组件要素与技术处理

一节课，教师不管讲解得如何详尽，总会有一些学生不太明白，或者是当时有些个别原因（如走神）而不能完全掌握一节课内容。在制作学习工具时，我想到了这一点，随时可以给学生再现刚刚结束的讲解过程。

在讲解《数形结合思想》时，传统的教学方法无法把首尾之间的过程讲解清楚。几何画板把图像的变化过程完全展现出来，而且每一次图形的变化过程，都清晰地显示了它们的相对的位置关系。

在平移加旋转的设计时，我把这个运动过程分解成平移和旋转，各自运动，然后将它们组合到一起，这样就会出现图形一边平移一边旋转的效果，逼真而直观。

评价与反思

决赛的整个过程，我一直在现场，说实话，可以说是高手如云，没有哪个人敢说自己的学习工具是完全优于别人的。因为大家都是各有所长，而且不同软件做的学习工具各有精彩之处。我对我自己的学习工具进行如下总结评价：①学习工具页面管理灵活；②可以无限次重复；③大大节省时间；④化抽象为形象；⑤运动变化，相对位置不变；⑥准确率高。

但是，多媒体归根结底是一个辅助工具，在使用过程中，也难免会有这样那样的问题：①学习工具的驻留性差，在使用过程中，用到下一页，就无法看到上一页。尤其是教师授课时，学生有时候无法及时回顾自己不会的内容；②醒目的颜色会刺激学生，也有可能诱使学生转移注意力，把学习工具的展示当成“热闹”而偏离了课堂的主题，达不到预期的效果。③学习工具准备时间太长，有时候很难跟上快节奏的高中课程。

幕前幕后

比赛过程中，选手们显然都做了精心的准备。数学化学习工具，突出的是工具的特点，平时的学习过程中，尤其是现在的高中学习，节奏普遍偏快，这就要要求学习工具不宜做得过大，能够对教育有所辅助，能够激发学生的兴趣，提高教师的授课的科学性，而且能够再次开发利用就足够了，而不是为了比赛而纯粹赶制这个“视频”。

我个人以为，今后在教学过程中，学习工具的制作得考虑到授课的进度和需要，如有些难点不易突破，可以作一个片段，让学习工具也微课化！这样可以节省时间，同样可以解决重点、难点，一举两得。期待下一次会有更好的学习工具“面世”。

评委印象

《数形结合思想》是一节高三复习专题课，数形结合思想在高考中占有非常重要的地位，它主要是把抽象的数学与直观的图形结合起来，本节课内容对提高学生的思维能力和数学素养很有帮助。在传统的课堂模式下，教师基本是在黑板上绘制一个静态的图像，然后通过手势比划进行讲解，教学效果不好，教学效率不高。展老师用几何画板所制作的《数形结合思想》学习工具，就能很好的突破这个难点。该学习工具有以下的一些优点。

印象一：化抽象为形象，让运动过程一目了然

通过学习工具使学生看到图形的运动变化过程，尤其是图像的形成转变过程。例如，学习工具中将三视图化为直观图，就很好地把图形的变化过程完整的展示在学生眼前，把原本只能“凭空捏造”的过程变得直观形象。

印象二：课堂教学容量大，效率高

在传统教学中，因为在绘制图形的环节就占了课堂的很多时间，所以教师一节课只能讲解4道左右的数形结合习题，这使得课堂的教学容量小、效率低。而本课的例题加练习达到了10道题目，使得课堂容量很大，从而实现高效课堂。

印象三：学习工具使用方便灵活。该学习工具既可以作为教师的课堂展示工具，也可以作为学生一对一的自学学习工具，使用方式非常灵活。

不过，本课也有一些地方值得商榷。例如，课堂容量太大，对学生的要求较高，基础差的学生可能跟不上；课堂比较传统，主要以教师讲授为主，不是很符合新课标中的以学生为主体，教师为主导的要求等。总的来说，无论是对教师还是对学生，《数形结合思想》仍不失为是一个优秀的数字化学习工具。

（点评人：NOC活动评委/广西南宁市第八中学 盘俊春）