一种冗余机械臂的轨迹跟踪联合仿真研究

沈志航，张新华，李 楠

（北京自动化控制设备研究所，北京 100074）

0 引言

为代替人类工位完成器件搬运、电子器件装配、元器件焊接等作业任务，现代工业机器人应具有末端执行器工作空间大，运动灵活，可实现空间避障、回避奇异构型等特点。根据作业任务要求，需对机械臂进行轨迹规划，计算出机械臂预期运动轨迹下相应的运动输入规律。传统的轨迹规划方法实质上是位置反解问题，即求出机械臂的位置反解方程，然后再将机械臂末端执行器的运动轨迹带入反解方程，从而得到与该运动轨迹相对应的各驱动关节的驱动参数。因此运动学逆解的难易程度直接影响着轨迹规划的精度乃至机械臂的应用范围。

现有6自由度机械臂在某些特殊情况下（如若干个关节轴线相交成90°，或者轴线平行），可以进行运动学逆解得到解析解，但其一个固定的末端位姿只对应着有限组关节角空间的解，这大大限制了机械臂操作的灵活性，影响了机械臂空间避障、回避奇异构型的能力[1]。

仿人型冗余机械臂在传统6自由度机械臂基础上增加了1个冗余自由度，可以使某一种末端位姿对应关节角空间的无限组解，在保证机械臂末端位姿控制的基础上，能够有效地实现避障行为[2-3]，回避奇异构型[4]等功能，不过，冗余自由度对求解机械臂运动学逆解带来很大困难。

多体动力学分析软件ADAMS是对机械系统的运动学与动力学进行仿真的专用软件，可以建立复杂机械系统的运动学与动力学模型。此外，可以利用其“一般点驱动”和“样条函数驱动”工具进行轨迹规划，避免了机械臂运动学逆解的复杂求解过程。然而，在实际应用中发现，单独利用ADAMS进行轨迹规划得到的机械臂关节运动速度、加速度存在突变，导致机器人末端产生振动，无法保证机械臂运行的平稳性。此外，单独利用ADAMS进行轨迹规划无法实现关节空间轨迹寻优，其得到的关节力矩无法为实际工程应用提供参考。

为解决上述问题，引入数据计算软件Matlab，它具有强大的数学计算能力，其ROBOTICS工具箱可进行轨迹规划与关节空间的轨迹寻优，得到的关节位移与速度曲线连续性好。以上述数据与ADAMS进行机械臂轨迹跟踪联合仿真，得到的关节加速度呈周期变化，没有急停等不良现象，各关节驱动力矩值没有突变，保证了机械臂轨迹跟踪运动的平滑性。

本文利用UG软件对冗余机械臂进行三维建模，利用ADAMS与Matlab进行器件搬运作业过程轨迹跟踪联合仿真，实现了机械臂对最优轨迹的跟踪，同时得到了所需的关节驱动力矩，为工程应用提供了参考。

1 冗余机械臂虚拟样机建模与坐标系的建立

1.1 冗余机械臂虚拟样机建模

机械系统三维模型作为对现实机械系统的描述，其建模的准确与否对于虚拟样机仿真分析的效果和精度有直接影响。动力学分析需要获得机械臂零部件的质量、惯性、质心坐标等信息，而这些参数的获取并非ADAMS的强项，故选择在UG环境下完成冗余机械臂的零部件模型绘制及装配。本文所设计的机械臂由3类模块化关节构成，可实现7自由度回转运动。其中肩部由3个关节组成，肘部由1个关节，腕部由3个关节组成。

肩部的偏转与俯仰关节由第一类模块化关节实现，其输出力矩较大；肘部俯仰关节与肩关节的滚动关节采用第二类模块化关节，起到连接与增加机械臂运动空间的作用。腕关节采用第三类模块化关节，用于末端执行机构的位姿的精细调整。为尽量拟合人体手臂，需对各关节重量、体积进行严格控制，为此关节内部采用永磁同步伺服电机串联谐波减速器的传动方式[5]。

机械臂作为一种复杂的机电系统，每个模块化关节内都包括机械系统、传感系统及驱动控制系统，需要对各部件进行简化处理。但UG环境下建立的机械臂三维实体模型虽然可严格描述实际机械臂系统，但是其机构复杂，直接利用此模型进行动力学、运动学仿真会导致运算量大、运算速度慢，不利于仿真的进行。

首先，忽略对整体运动分析影响较小的零部件，如间隙调整垫片、螺钉等紧固件；其次，分析机械臂运动机理，利用布尔操作将关节输出套筒、谐波减速器柔轮和电机转子等主要运动部件合为一体。同时将对运动部件进行约束和控制的部件，如电机外壳、谐波减速器刚轮等合为一体。最后，将经过简化的机械臂模型从UG导入ADAMS中，使用aggregate mass工具快速检查系统的质量和转动惯量，使用Table Editor快速检查并处理每个部件的质量和转动惯量方面可能出现的问题。确定经过简化的机械臂模型可较为真实地反映机械臂实体状态，在各关节处添加旋转副约束，并设定关节摩擦系数及间隙等参数。完成ADAMS环境下的机械臂建模过程，生成的冗余机械臂虚拟样机如图1所示。

图1 冗余机械臂虚拟样机Fig.1 The virtual prototyping of redundant manipulator

1.2 冗余机械臂坐标系与连杆结构参数

为了描述机器人各杆件和终端之间的转动或移动关系，需要建立机器人关节坐标系，Denavit和Hartenberg于1955年提出了D-H矩阵法[6]。根据此方法建立机械臂初始状态下D-H坐标系，如图2所示。

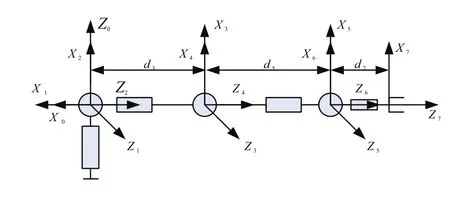
图2 机械臂初始状态D-H坐标系Fig.2 The D-H coordinate system of robot arm on initial state

由图2坐标系得到表1所示的机械臂连杆结构参数，这些参数用于在Matlab环境下建立机械臂对象。

表1 机械臂连杆结构参数Tab.1 Link structure parameters of the robot arm

3 联合仿真系统建模

3.1 轨迹跟踪曲线的获取

机械臂搬运器件作业可视为点到点轨迹跟踪，运动过程中机械臂末端姿态保持不变，机械臂携带元器件在笛卡尔空间内走过一条直线。对此运动过程进行轨迹规划，作为运动期望值的各关节转角曲线的求取非常重要，要求首先对其进行优化，然后以此作为联合仿真系统的期望值，这样联合仿真得到的结果才能够保证[7]。Robotics Toolbox是Matlab的机器人工具箱，它采用七阶多项式对轨迹规划进行插值，并结合速度、加速度零边界条件进行运算，实现了关节空间轨迹寻优[8]。

利用Robotics工具箱进行轨迹规划，首先需要应用link函数和robot函数结合连杆结构参数建立机械臂初始状态下的模型。针对器件搬运作业任务，利用transl函数将机械臂进行平移，变换到器件初始位置，得到轨迹规划初始状态的齐次变换矩阵T0。然后再进行第二次平移变换得到机械臂终止状态下的齐次变换矩阵T1。最后利用笛卡尔空间轨迹规划函数CTRAJ对机械臂从T0至T1进行轨迹规划，得到冗余机械臂7个关节转角与时间的关系，即为联合仿真轨迹跟踪的期望曲线值。

3.2 联合仿真机械臂子系统建模

冗余机械臂虚拟样机在ADAMS环境中生成，而控制策略则在Matlab中建立。为实现ADAMS与Matlab的实时数据交换，需要建立一组二者均认可的状态变量。针对此机械臂，需建立两类系统变量：各关节电机所需的控制力矩、各关节的方位角。其中关节控制力矩与机械系统的输入变量关联，关节的方位角与输出变量关联。ADAMS/Controls模块实时调用控制系统输出的转矩变量值驱动关节运转，同时机械臂各个关节的实际方位角又被实时反馈到控制系统中，从而构成完整的闭环控制系统，实现关节位置的实时跟踪[9]。

最终，由Matlab软件生成了机械臂子系统模块，其中的期望关节转角及相应的实际关节转角如表2所示，且angle1～angle7分别对应表1中的变量θ1～θ7。

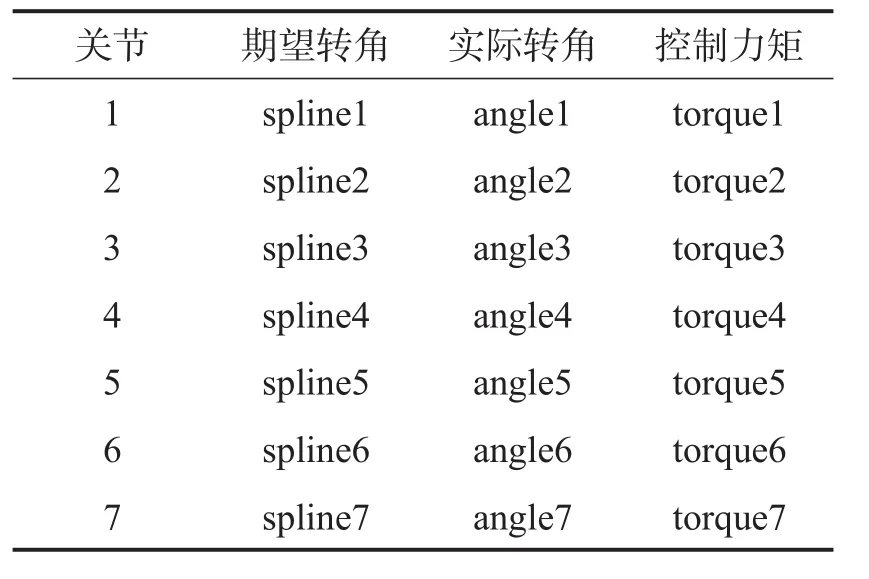
表2 机械臂子系统变量Tab.2 System variables of the robot arm

3.3 联合仿真位置伺服系统建模

机械臂子系统及期望跟踪曲线确定后，即可以此为基础搭建控制系统框图。对每个关节位置角度分别应用PID控制策略进行控制，以使机械臂末端跟踪预期的运动轨迹。最终得到的联合仿真控制系统如图3所示。

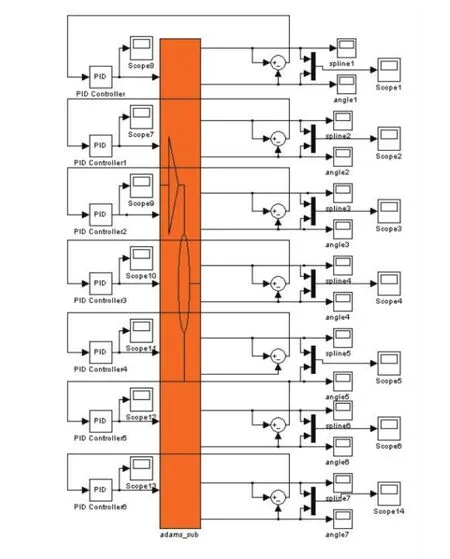
图3 联合仿真控制系统Fig.3 Control system of coordinated simulation

4 轨迹跟踪联合仿真试验

4.1 轨迹跟踪效果分析

联合仿真系统搭建完成后，即可对机械臂进行轨迹跟踪实验，在验证机械臂跟踪特性的同时，可以获得此运动轨迹下机械臂关节控制力矩，为工程应用提供可靠参考。经过仿真，逐一调节PID参数，得到各关节跟踪曲线如图4所示。其中Angle1～Angle7分别表示从肩部1关节至腕部3关节的转角。

仿真结束后观察机械臂各关节实际转角与期望转角曲线发现，通过联合仿真可以控制机械臂系统的每个关节转角以较小的延迟跟踪期望转角，其最大偏差为0.05134rad，满足高速运动下机械臂的控制需求，从而实现机械臂末端对期望轨迹的准确跟踪。

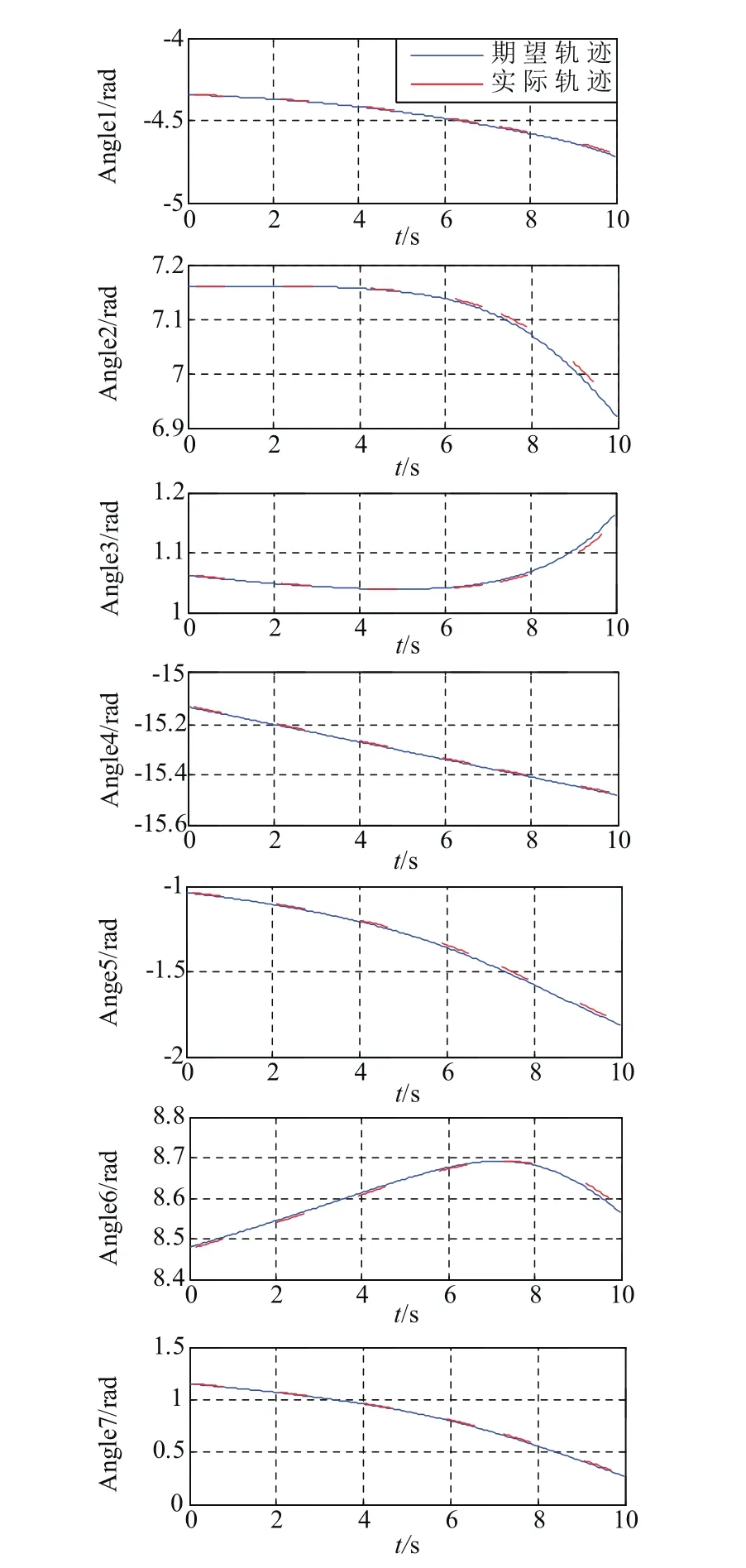
图4 机械臂关节跟踪特性曲线Fig.4 The track-following characteristics of robot arm

4.2 轨迹跟踪过程中的关节加速度及驱动力矩控制

在实现轨迹跟踪的同时，可由ADAMS软件测量得到机械臂各关节转角的加速度曲线，如图5所示。

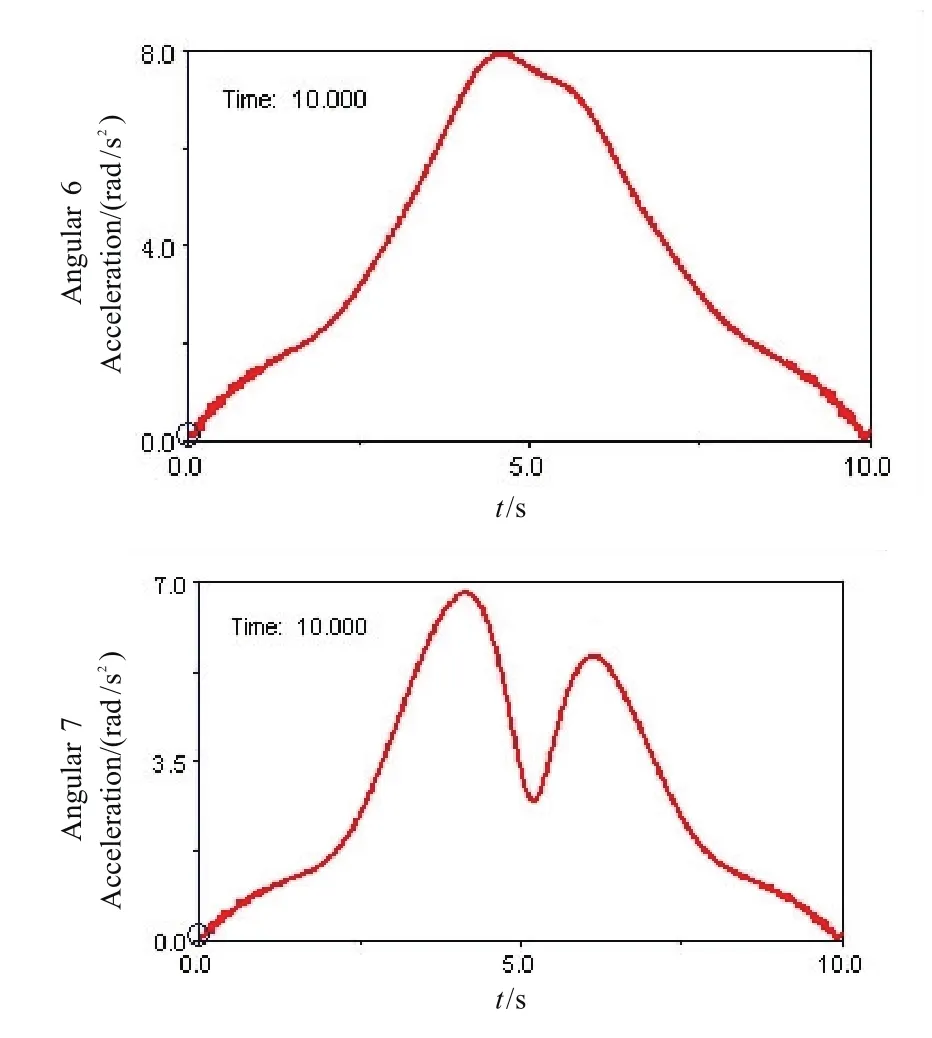
图5 联合仿真轨迹规划得到的关节加速度曲线Fig.5 The acceleration curve got by coordinated simulation

分析图5发现，联合仿真得到的机械臂关节加速度曲线连续、平滑，没有突变点，因此机械臂运行平稳、可靠，证明联合仿真进行的轨迹规划，在迅速跟踪关节期望转角轨迹的同时，实现了对关节加速度的控制。此外还可得到相应于此实际转角所需要的关节驱动力矩，如图6所示。

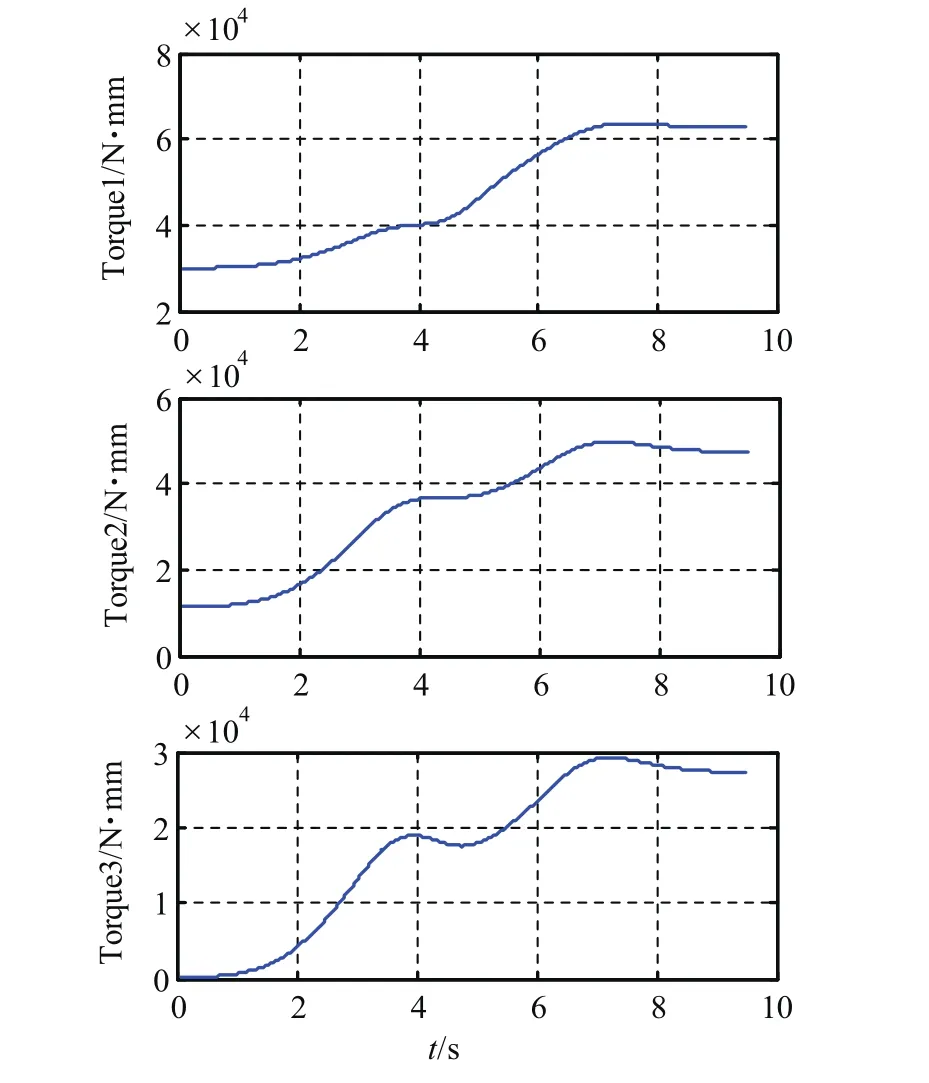
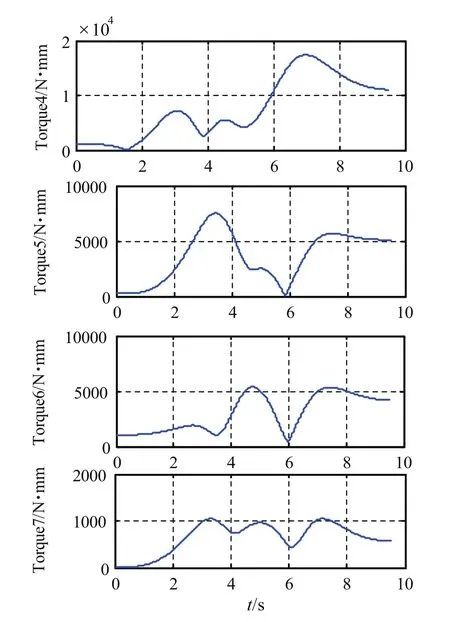
图6 机械臂1至7关节驱动力矩Fig.6 The driving torque of each joint got by coordinated simulation

分析各关节驱动力矩发现，由Matlab进行轨迹规划得到的关节转角运行平滑，所需的关节驱动力矩值没有突变。由于在ADAMS环境下考虑了机械臂重力力矩的平衡，个别关节处驱动力矩的初始值不为0，与实际情况相符，证明联合仿真方法适用于实际工程应用。

5 结论

本文应用虚拟样机技术，利用UG创建仿人冗余机械臂三维实体模型，以此为基础进行ADAMS与Matlab联合仿真，避免了复杂的传递函数与动力学模型的搭建。应用Matlab Robotics工具箱对此机械臂的某项实际工作任务进行轨迹规划，得到优化的关节空间转角。以此转角结果为期望值对机械臂进行联合仿真研究，结果证明机械臂轨迹跟踪效果良好；仿真得到的关节加速度平滑、连续无突变点，保证机械臂在跟踪轨迹的过程中运行平稳；得到的机械臂关节驱动力矩平滑，数值合理，可为实际工程应用提供可靠参考。

[1]Primrose E J F.On the input-output equation of the gen eral 7R-mechanism[J].Mechanism and Machine Theory,1986,21（6）:509-510.

[2]Kwang-Kyu L,Komoguchi Y,Buss M.Multiple obstacles avoidance for kinematically redundant manipulators using Jacobian transpose method[C]//.Annual Conference on SICE.Piscataway,NJ,USA:IEEE,2007:1072-1076.

[3]Baillieul J.Avoiding obstacles and resolving kinematic redundancy[C]//.IEEE International Conference on Robotics and Automation.Piscataway,NY,USA:IEEE,1986:1698-1704.

[4]吴伟国.冗余度机器人运动学基本理论与7自由度仿人手臂的研究[D].哈尔滨：哈尔滨工业大学，1995.

[5]蒋新松.机器人学导论[M].沈阳:辽宁科学技术出版社,1994.

[6]DENAVIT J,HARTENBERG R S.A kinematic notation for Lower-pair mechanisms based on matrices[J].Trans ASME JApplMech,1955（23）:215-221．

[7]翟敬,梅康博,张铁.六自由度喷涂机器人动力学分析及仿真[J].机械设计与制造，2012（1）:169-171.

[8]左富勇,胡小平,谢珂,等.基于Matlab Robotics工具箱的SCARA机器人轨迹规划与仿真[J].湖南科技大学学报:自然科学版,2012,27（2）：41-44．

[9]任远，白广忱.基于ADAMS与Simulink的机电一体化系统联合仿真[J].机电一体化,2009（6）:31-34.