加速度计全量程标度因数不对称性标定算法研究
2015-07-09于湘涛
王 洋,于湘涛,吴 楠,魏 超,张 吉
(北京自动化控制设备研究所,北京 100074)
0 引言
加速度计是惯性导航系统的核心器件之一,广泛应用于航空、航天、船舶以及兵器系统的导航制导与控制中[1]。标度因数不对称性作为惯导系统速度误差的影响因素之一,其标定精度的提高对惯导系统导航精度的提升具有重要意义。
标度因数不对称性是对加速度计在正向、负向输入加速度条件下标度因数差异性的一种度量[2]。目前加速度计标度因数不对称性研究多见于重力场环境,随着加速度计指标精度的提高和输入量程的增大,需要对全量程范围内的标度因数不对称性进行研究[3-4]。
目前加速度计全量程高阶非线性系数大多通过精密离心机试验进行标定,而试验过程中由离心加载引起的各种误差,对其标度因数和偏值等线性指标的标定精度影响较大。如何辨识加速度计精密离心机测试过程典型误差,并进行误差控制,是进行全量程标度因数不对称性标定的关键。
1 加速度计精密离心机测试误差分析与数据处理方法
精密离心机测试是对加速度计高过载特性进行测试的常用方法,利用离心机产生的高g值的持续向心加速度作为加速度计的输入,用于测量与标定加速度计与高过载有关的各种误差系数[5]。
1.1 加速度计精密离心机测试误差分析
在加速度计精密离心机测试过程中,由于测试设备与测试方法的局限,会产生各种误差。文献[6]将其归纳为半径不确定性、对准不确定性、角速度误差、加速度计温度影响、试验过程中的趋势项,以及加速度计信号测量误差等方面。各类误差与加速度计输出系数的对应关系如图1所示。

图1 加速度计精密离心机测试典型误差Fig.1 The typical errors in accelerometer precision centrifuge testing
精密离心机测试的主要问题是半径不确定性与对准不确定性。其中半径不确定性影响因素包括静态半径的不确定性、半径的动态变化和由于环境导致的半径变化[6-11]。
1)静态半径不确定性
为确定待测加速度计有效质量中心的静态半径,需要明确大臂的中心位置、有效质量中心相对于加速度计基准面的位置以及这些位置之间所有机械构件的尺寸和相互关系。大部分离心机不能提供直接测量静态半径的手段,在实际过程中静态半径一般通过待测加速度计的输出来估算。
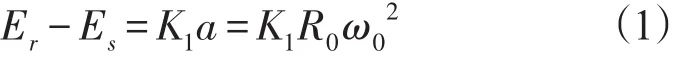
式中:R0为离心机静态半径,Er为离心机旋转时的输出平均值,Es为离心机静止时的输出平均值,K1为当前环境下的标度因数值。
2)离心机大臂伸长
大臂伸长是指连接加速度计和离心机旋转轴的机械结构超出静态值R0的伸长,由离心加载引起。仅考虑大臂伸长影响,实际的半径方程为:

式中:R为实际转臂长度,R0为离心机转臂静态值,CAS为常数,与转臂材料等相关,量纲为加速度的倒数,a0为标称向心加速度。
3)加速度计检测质量偏移
在离心加载作用下,检测质量偏移导致加速度计有效质量中心半径的变化,其影响机理与大臂伸长相似,均正比于施加的向心加速度。
4)加速度计正负向安装不对称性
加速度计有效质量中心的位置在微小范围内不可测定,当待测加速度计输入轴倒置时,径向位置会产生误差,会导致输出数据的标度因数不对称性,从而恶化线性度系数的评估。此外,径向不对称性还会严重影响偶次项系数。
在精密离心机测试过程中,由于离心加载作用,无论加速度计正向或负向安装,大臂伸长、敏感质量偏移等都会加大输入加速度的数值,即输入加速度正向时表现为正,负向时表现为负,即奇异二次项系数。在精密离心机标定时,必须对奇异二次项系数加以考虑,否则会对其它系数标定精度产生影响。
1.2 加速度计精密离心机测试数据处理方法
加速度计模型方程是表述加速度计输出E与沿加速度计基准轴作用的加速度之间关系的表达式,完整的加速度计输出模型方程如式(4)所示。
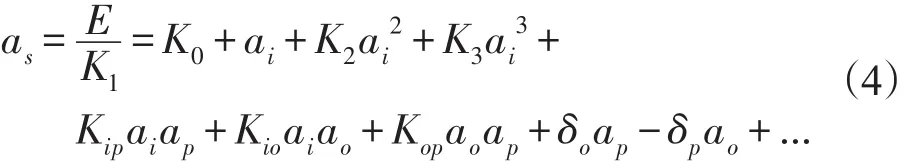
式中:E为加速度计输出,ai、ao、ap分别为沿输入轴、输出轴和摆轴的加速度,K0为偏值,K1为标度因数,K2、K3为高次项系数,Koq为奇异二次项系数,Kip、Kio、Kpo为交叉耦合系数,δo、δp为安装误差角。
在测试过程中,受静态半径不确定性、离心机大臂伸长、敏感质量偏移和安装误差等因素影响,真实的加速度计输出模型如式(5)所示。
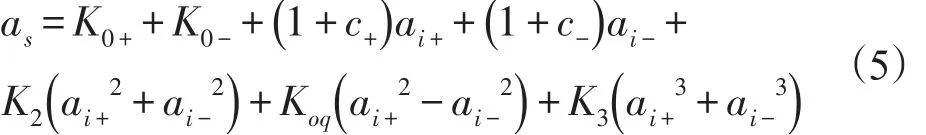
为便于运算,将式(5)重新排列如式(6)。
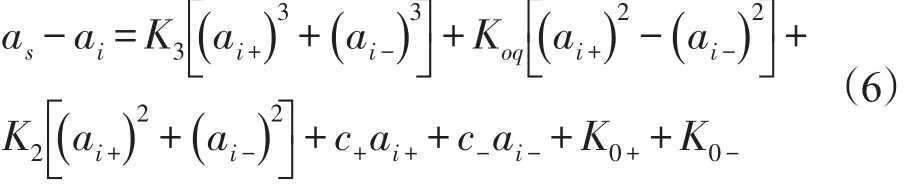
其中,带有下标+的项仅当ai>0时适用,带有下标–的项仅当ai<0时适用,as为加速度计输出值,ai为沿输入轴IA的加速度,c-ai-、c+ai+为由于半径测量和安装误差引起的估算输入加速度误差的一次近似值。
为充分利用试验数据,尽可能的减小误差,构造与求解参数相关的测试数据矩阵A,求解系数矩阵K以及输出矩阵B,三者之间关系如式(7)所示[6]。

对于式(7),根据最小二乘算法,存在正规方程ATAK=ATB,应用矩阵逆变法,得到系数矩阵如式(8)。

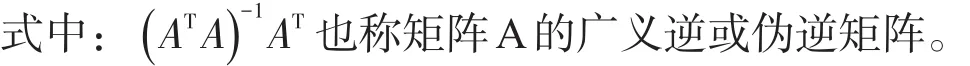
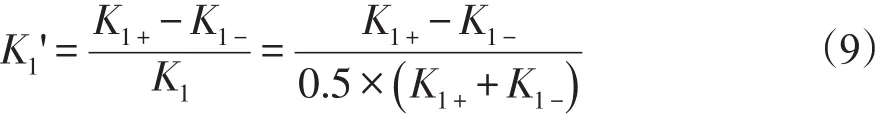
式中:K1'为标度因数不对称性,K1+为正向标度因数,K1-为负向标度因数。
在精密离心机测试中,由于离心加载引起的各种误差,对线性项标度因数K1、偏值K0的标定精度影响较大,进而影响到全量程标度因数不对称性的标定。为改善精密离心机测试对加速度计线性指标的标定,在典型误差分析的基础上,给出利用精密离心机试验进行加速度计全量程标度因数不对称性标定的原则:以标度因数误差c-、c+作为测试过程精度指标,对输入数据进行迭代,直至c-、c+降低到10-8水平。对修正后的数据进行三阶拟合,得到加速度计全量程标度因数不对称性。
加速度计全量程标度因数不对称性标定流程如图2所示。
2 加速度计全量程标度因数不对称性标定算法
加速度计标度因数不对称性是对正向、负向加速度输入条件下,标度因数差异性的一种度量。在实际应用中,一般用正向与负向输入加速度测定值的差值与其平均值的比值进行衡量,即:
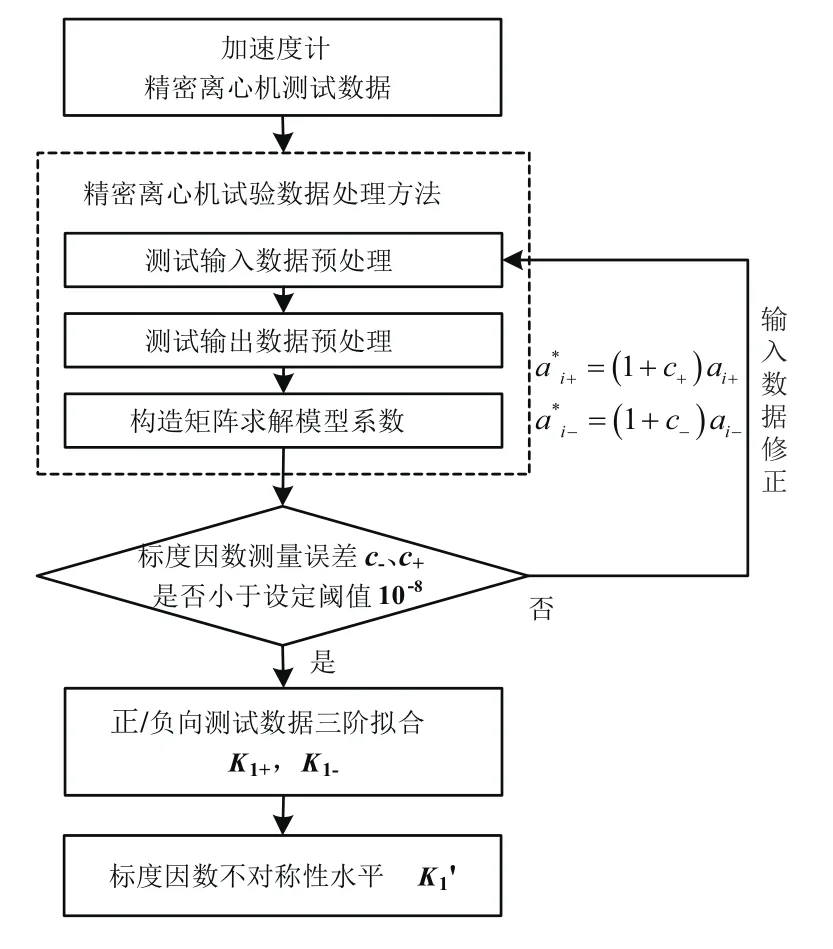
图2 加速度计全量程标度因数不对称性标定流程Fig.2 The calibration steps for accelerometer full-range scale factor asymmetry

3 试验验证
为验证文中提出的标定算法,抽取10只加速度计进行精密离心机试验。试验结束后,按照上述算法计算出测试数据修正前后的标度因数误差c-、c+,如表1所示。

表1 标度因数误差c-、c+修正前后对比Tab.1 Acomparison of scale factor errors between the original and revised testing datas
从表1可以看出,通过输入数据修正,标度因数测试误差c+、c-快速收敛,从10-4降低至10-9,证明了通过测试数据修正,能够有效降低离心机测试误差对加速度计线性系数标定精度的影响。
对修正后的测试数据,应用式(10)进行三阶多项式拟合求取标度因数,并与重力场下标度因数标定值进行对比,如表2所示。

表2 重力场与离心机标度因数标定值对比Tab.2 Acomparison of scale factors in gravity field and precision centrifuge testing
从表2可以看出,加速度计精密离心机测试数据修正后,应用三阶拟合得到的标度因数标定值与重力场标定值非常接近(相差10-4水平),证明了通过数据修正能够得到较高精度的标定因数标定值,也为全量程标度因数不对称性标定奠定了基础。
对修正后的测试数据,计算正向标度因数K1+、负向标度因数K1-,并应用式(9)得到全量程范围内标度因数不对称性水平K1',如表3所示。
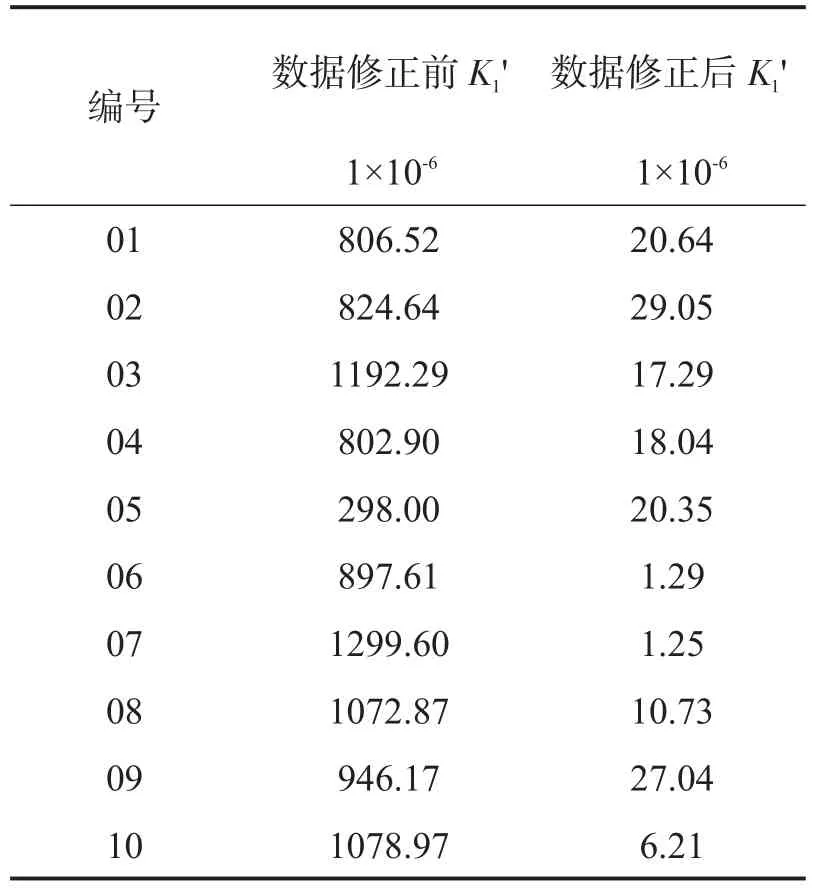
表3 加速度计全量程标度因数不对称性K1'标定结果Tab.3 Acomparison of full-range scale factor asymmetry between the original and revised testing data
从表3可以看出,利用文中提出的算法对加速度计测试数据进行修正后,可以将标度因数不对称性K1'从10-4提高至10-5,提高了加速度计全量程标度因数不对称性的标定精度。
4 结论
重力场四点翻滚法是加速度计标度因数K1和偏值K0标定的常用方法,但由于仅能提供-1g~1g输入加速度,无法给出全量程标度因数不对称性K1'的有效信息。而精密离心机测试由于测试过程引入的各种误差,不能直接实现对加速度计标度因数的精确标定。
在加速度计精密离心机测试误差分析的基础上,提出了一种加速度计全量程标度因数不对称性标定算法,并对其进行了验证。验证结果表明,文中提出的算法能够将标度因数测试误差c-、c+从10-4降低至10-9,标度因数不对称性K1'的标定精度从10-4提高至10-5。
[1]吴亮华,郑辛,李群,等.高精度激光捷联惯导行进中方位对准技术[J].战术导弹技术,2008(1):73-78.
[2]GJB 1037A-2004.单轴摆式伺服线加速度计试验方法[S].
[3]赵连元.石英挠性加速度计目前测试方法的局限性分析[J].战术导弹控制技术,2005,49(2):72-77.
[4]蒋效雄,刘雨,苏宝库.高精度加速度计重力场标定试验方法[J].吉林大学学报(工学版),2010.4(1):287-291.
[5]JJF 1116-2004.线加速度计的精密离心机校准规范[S].
[6]Std 836TM-2001.IEEE recommended practice for precision centrifuge testing of linear accelerometers[S].The Institute of Electrical and Electronics Engineers.
[7]安金刚,王珺,张兰.石英挠性加速度计精密离心测试的非线性系数重复性探讨[J].战术导弹控制技术,2006,53(2):80-82.
[8]邢海峰,任顺清,祁家毅,等.加速度计二次奇异项系数的形成机理与标定方法[J].航天控制,2009,27(2):91-95.
[9]乔仁晓,孟晓风,季宏.加速度计非线性项系数校准误差分析与建模[J].系统仿真学报,2008,20(6):1633-1635.
[10]徐永,贺忠江,乔仁晓,等.线加速度计高次项系数校准初探[J].计测技术,2008,28(5):14-19.
[11]王世明,任顺清.精密离心机误差对石英挠性加速度计误差标定精度分析[J].宇航控制,V33(4):520-526.
