“学为中心”初中数学“1+2”学案设计的实践研究

张红

笔者所在单位在学习了山东杜郎口中学的教学改革后，开展了“学为中心”初中数学“1+2”学案教学模式改革，经过两年多的实践证明，“学为中心”初中数学“1+2”学案教学模式不但有效提高了学生的学习成绩，而且提高了学生的自我学习能力和数学素养.笔者所在单位的“1+2学案” 在设计方面紧紧结合本校学生的学情， 并非机械模仿各兄弟学校的“学案”， “1+2学案”由“课前预学案，课中导学案和当堂检测题”三部分构成.在学科的具体内容设计上紧扣“学为中心”，在这样的设计理念下，“1+2学案”更像一个引导者，引导学生如何学会学习，学会提出问题，分析问题，解决问题.本文研究了兄弟学校“学案”的一些不足之处，结合两年多的“1+2学案”教学实践改革，总结了本单位的“学为中心”初中数学“1+2”学案的基本模式和特色.

一、“学案”设计中存在的问题

当前学案在教学实践中存在诸多问题，学案的设计形式大于内容，学案设计中没有突出学生的“学” 的内容和活动.很多学校编制的学案在实践中都存在这样的现象：学生课前“做学案”;课中交流、 展示“学案”;课后“再做下一个学案”.这样的“学案” 违背改革初衷.学案在教学实践中存在的问题一：学案等同于教案.即将老师的讲义，简单处理，下发给学生，把我们课堂教学最后要呈现的结果和要探究问题的答案全都交给了学生.这种做法没有引导学生们去思考，忽略了学生“发现问题”、“分析问题”和“解决问题”的过程.其结果仍是以教师的“灌输”为中心.问题二： 学案等同于教材.很多学案都是对教材内容简单整合后，把课本的例题和课后的习题不加选择直接摘抄到学案上，没有抓住新知识的“生长点”去设计问题，根本没有体现学案的价值，没有体现课堂上学生的主体地位.问题三：学案等同于练习卷.一些学案整个都以试题的形式出现，致使整节课都是学生解题，教师在课堂上就是帮助学生解决这些题目，这不符合学生认知发展规律，忽视了学生的最近发展区，长此以往，优者产生厌学情绪，差者抄袭导学案，使得学生逐渐对学习失去兴趣.

二、“学为中心”初中数学“1+2”学案设计的基本模式探究

（一）“学为中心”初中数学“1+2”学案设计的流程图

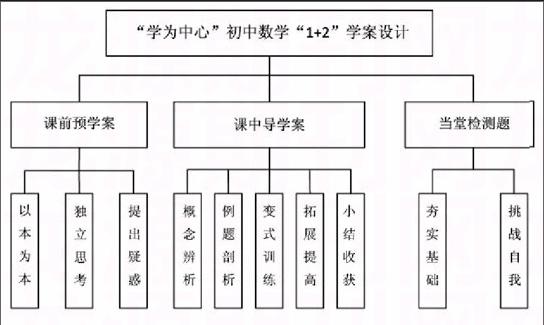
笔者所在的数学教研组在两年多的“学案”教学模式实践改革中，及时总结失败和成功的经验教训，经历多次教研，听课，磨学案，最终形成具有本单位特色的“三环节，五步骤”数学“1+2”学案设计模式，基本模式如下图所示：

（二）“学为中心”初中数学“1+2”学案设计的环节

“学为中心”初中数学“1+2”学案设计从以下四大方面着手设计.

1.完善学习环节——“学”为中心的“绝招”

“学为中心”初中数学“1+2”学案分为课前预学案，课中导学案及当堂检测题三大学习环节.三大学习环节分工明确：①课前预学案——清晰学习内容和研究问题;②课中导学案——夯实基础，突破难点，拓宽思维;③当堂检测题——巩固知识，查漏补缺，实现课课清.三个环节的设计，环环相扣，目标清晰，很好地培养了学生课前学习，课中思考，及时巩固的学习习惯.

2.以“课前预学案”为先导，打造“有思考的预习”

在两年多的“学为中心”初中数学“1+2”学案设计与实践研究中，笔者所在学校在对课前预学案的设计及实施过程中争论最多.课前预习作为一种科学的学习方法，不仅在整个学习知识的过程中起着重要的作用，而且在培养学生良好的学习习惯及提高自学能力方面有着不可低估的作用.但是也有老师认为课前预习会让学生失去探究学习的机会，认为完成课前预学案实际上是增加了学生的作业负担，而且老师要在上课之前把课前预学案先批改出来也存在时间上的困难.围绕着这些问题，笔者所在学校数学组对课前预学案的设计研讨不止10次.预习是对课堂教学的准备，而这种准备不只是学生对于教材的提前阅读或者是对于课后习题的提前练习，更重要的是为了能在课堂学习中，更好地实现自主、合作、探究的学习.我们可以通过研究预习的内容与方式，来提升预习的功能.如何尽量减轻学生学业负担？如何高效开展预习？如何让学生有思考地预习？为了解决以上三个问题，笔者所在学校结合学生实际，开展了“三步骤”预习法.具体操作如下：

步骤一：以本为本——指导学生学会看数学课本.

步骤二：独立思考——对教师设计的预习案的问题进行独立研究.

步骤三：提出疑惑——预习本课后提出自己还有困惑的地方.

为最优实现三步骤预习法的实效性，在开学之初，指导学生学会看数学书，让学生明确先看书，再完成相应课前预学案.同时对教师设计课前预习案也提出了较高的要求，要求教师深挖课本概念和例题的本质，从提升学生思维的角度，提出2～3个有思考价值且有助于提升数学思维品质的思考题，问题少而精，尽量不增加学生的学习负担，把更多的时间留给学生思考，学生可以在预习后，写下在预习过程中可能存在的困惑.下面以浙教版《义务教育课程标准实验教科书数学》八年级下册“5.3正方形”第一课时为例，对课前预学案的设计如下：

【课前预学案】

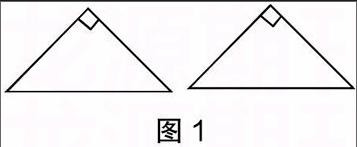
（1）如图1，有两个全等的等腰直角三角形，你能拼出矩形吗？ 你能拼出菱形吗？

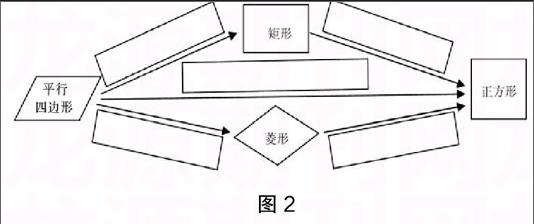
（2）阅读教材中的本节内容后，请在下列方框中填入正方形与矩形、菱形、平行四边形的关系（如图2）.

（3）预习后，你还有什么疑惑之处，请把它写出来.

3.课中导学案“环环相扣”，打造高效课堂的“诀窍”endprint

高效课堂不仅仅是优等生的课堂，更是后进生的课堂.为了每个学生都能够在数学课堂上成为真正的学习者，实现全体学生的共同进步，笔者所在学校开展了以课中导学案为引导的五步骤课堂教学法打造“精致”课堂.通过小组互助式答疑，教师引领答疑，从而让学生多学，乐学.五步骤课堂模式操作法是：

步骤一：概念辨析——检测预习效果，对课中概念辨析，使概念“精致”.

步骤二：例题剖析——生生互助答疑，交流分享中“学”，使例题“经典”.

步骤三：变式训练——教师引领答疑，在解决问题中“学”，使思维“发散”.

步骤四：拓展提高——小组合作展示，在亲历体验中“学”，使能力“发展”.

步骤五：小结收获——学生自主小结，收获文本体现，使知识结构“完善”.

下面还是以“正方形”第一课时为例，对课中导学案的设计如下：

【课中导学案步骤一】

（1）解决预学案中的第1个问题，并写出正方形与平行四边形、矩形、菱形的包容关系，如图3.

（2）解决预学案中的第2个问题.

（3）写一写：如何判定一个图形是正方形.

①定义法：            ;②菱形法            ;

③矩形法：            .

（4）概念辨析——下列说法对吗？

①四个角都相等的四边形是正方形.（   ）

②四条边都相等的四边形是正方形.（   ）

③对角线相等的菱形是正方形.（   ）

④对角线互相垂直的矩形是正方形.（   ）

⑤对角线垂直且相等的四边形是正方形.（   ）

⑥四边相等，有一角是直角的四边形是正方形.（   ）

⑦对角线互相垂直，一个角是直角的四边形是正方形.（   ）

【课中导学案步骤二】

（5）课本例题剖析：已知：如图4，在Rt△ABC中.∠ACB=90°，CD是∠ACB的平分线，DE⊥BC，DF⊥AC，垂足分别是E，F. 求证：四边形CFDE是正方形.

【课中导学案步骤三】

变式1：在上例题中，若增加条件AC=4，BC=3，其他条件不变.你能求出AD与BD的长吗？

变式2：如图5，在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E，F.请添加一个条件，使四边形EDFA是正方形.请你至少写出两种不同的添加方法（不另外添加辅助线）.

配套练习：课本P125.作业题4，5.

【课中导学案步骤四】

拓展提高：

（1）一张矩形纸片，要折叠出一个最大的正方形，小明把矩形的一个角翻折上去，使相邻的两直角边重合，则可以折出一个最大的正方形.问小明利用的数学原理是              .

（2）如图6，大正方形的边长为2，小正方形的边长为1，怎样把大正方形剪成四块，与小正方形拼成一个边长为 的正方形？

设计意图：第1题是一个在日常生活中常用的折纸方式却蕴含着“邻边相等的矩形是正方形”的正方形判定定理，充分体现数学来源于生活又服务于生活. 第2题是一个设计题，有一定的难度，在拼成四边形后，还要观察四边形的边和角，从正方形的三个判定定理出发去验证.

【课中导学案步骤五】

（1）梳理，如图7.

（2）反思及解惑：通过本节课的学习，你一定有很多感想和收获，相信你一定可以解决同伴的疑惑，那就试一试吧！

4.当堂检测题夯实基础实现当堂巩固

根据教学目标和教学实情，确定检测试题，试题的编制包括两块内容，一是由基础题构成的“夯实基础”，注重对基础知识和基本技能的考察，试题比较简单.二是由稍难题构成的“挑战自我”，注重对数学思维的拓展和提升，试题有一定的难度.在课堂教学中，预留5分钟测查以检查教学效果和导学案的质量，由于检测的时间较短，所以题量严格控制在3题左右.教师要根据教学目标设计题目、按知识点分层次设计题目、题型应与中考吻合，设计题目时要重内容，不要追求形式.当堂检测不仅能够检测课堂教学的效果，更是减轻了课外负担.下面以“正方形”第一课时为例，对当堂检测题的设计如下：

【当堂检测题之夯实基础】

（1）已知在四边形ABCD中，∠A=∠B=∠C=90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（   ）.

（A） ∠D=90°        （B） AB=CD

（C）  AD=BC         （D） BC=CD

【当堂检测题之挑战自我】

（2）如图8，点O是线段AB上的一点，OA=OC，OD平分∠AOC交AC于点D，OF平分∠COB，CF⊥OF于点F.

①求证：四边形CDOF是矩形;

②当∠AOC多少度时，四边形CDOF是正方形？并说明理由.

当堂检测确保学生能够把刚学的知识转化为能力.让每位学生独立完成后，写上名字，同桌互改，可以由学生或老师公布答案，并对疑难问题进行解释反馈.这样做不仅有利于培养学生课上全神贯注、快速高效的学习能力，同时也能较为准确地反馈出学生的学习情况，便于老师针对性指导，改进教学.

三、结束语

在浙教版八下的第四章“平行四边形”及第五章“特殊平行四边形”的教学中，笔者都采用了以上模式的“1+2”学案，教学收到了很好的效果.在“特殊平行四边形”的学习中，学生在自主合作探究中，不仅得到了特殊平行四边形（矩形、菱形、正方形）的一系列判定定理，而且掌握了 “猜想—证明—得出结论”的数学思想方法.当然，不同课型学案应结合课型特点进行编写，比如习题课就不能完全照搬以上“三环节，五步骤”的设计模式，而且不是所有的数学内容都适合“1+2学案”，有些知识用“1+2学案”能取得很好的效果，而有些却不能达到应有的效果.因此，什么内容是适合制作“1+2学案”的，什么内容不适合“1+2学案”也值得我们进一步研究.endprint