有效设计探究活动

孙红伟

摘要：新课程标准的课堂教学重点由注重学习结果转向注重学习过程，这就给教师提出了新的要求，即教师的教学行为能给学生提供去体验探究学习的过程和经历的机会，最终有效促进学生教学知识的自主建构。探究性学习是一种积极的学习过程，学生以某个问题作为突破点，通过质疑、调查、分析、交流等活动，获得知识，激发情趣，掌握方法。如何增强学生探究的自信心和求解问题的耐心，提高学生参与学习活动中主动进行决策的兴趣、意识和能力，需要有效设计探究活动。

关键词：体验；探究；自主建构；兴趣；意识；能力

中图分类号：G623.5文献标识码：A 文章编号：1992-7711（2015）09-074-2

教学《多边形的面积计算》这一单元的内容时，考虑到小学五年级学生已经具有一定的抽象思维能力，应鼓励学生主动探求知识，激发学生学习的兴趣和探究欲，给予学生充足的时间和广阔的空间，并挖掘出教学内容中蕴含的丰富价值。

激发探究的欲望

探究是一种需要，探究欲实际上就是一种求知欲，它解决的是“想不想”探究的问题。课堂教学中，教师的一个十分重要的任务就是培养和激发学生的探究欲望，使其处于一种探究的冲动之中。

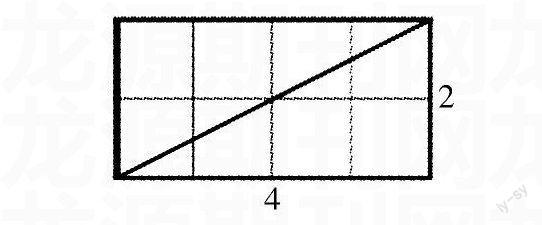
如教学《平行四边形的面积》，课前为每位学生准备下面的一份材料。

（每个小方格表示1平方厘米）

师：计算长方形的面积可以用相邻的长和宽相乘来计算，计算平行四边形的面积也可以用这种方法吗？

生1：长方形的长和宽相交成直角，而平行四边形相邻的两条边相交成的不是直角。

生2：长方形的面积是8×5=40（平方厘米），如果平行四边形也这样计算，感觉平行四边形的面积比长方形小了一点。

生3：如果我们把左边的一块三角形剪下来平移到右边，正好能拼成一个长方形，长方形的长还是8厘米，只是宽变成了4厘米。

生4：4厘米其实是平行四边形的高，平行四边形的面积应该用底乘高来计算。

师：到底是8×5还是8×4？请利用手中的工具验证自己的猜想。

很快，学生将探究的方向聚焦于平行四边形转化为长方形上，学生探究的欲望被激发了出来，剪、拼得十分熟练。对于不同意见，学生觉得有必要去探究；对于似曾相识的算式，学生觉得有方向去探究，探究的主动性和欲望不言而喻。

扩展探究的空间

长期以来，学生习惯于按照书上写的与教师教的方式去思考问题，用符合常规的思路和方法解决问题，这对于基础知识和基本技能的掌握是必要的，但对于数学兴趣的激发，智力能力的发展，特别是创造性思维的发展，显然是不够的，课堂上应给予学生充足的时间和广阔的空间，引导学生动手实践、自主探索、合作交流。

如教学《三角形的面积》，教科书后面的三角形，笔者没有布置学生剪下来，但要求他们带剪刀来。

师：我们已经知道通过剪、拼将平行四边形转化成长方形，如何计算三角形的面积呢？

学生议论开了，有的说转化成长方形，有的说转化成平行四边形。

生1：将直角三角形的两条直角边相乘，就是一个长方形的面积，除以2就得到直角三角形的面积，也就是直角三角形的面积等于底乘高然后除以2。

笔者继续问道：“锐角三角形和钝角三角形的面积也可以这样计算吗？”这个学生果然没有让笔者失望，他把课本投放到展台上，继续说道：“用三角形的底乘高得到长方形的面积，每个三角形的面积正好是长方形面积的一半。”

还有的学生想到了下面的方法：“将上面的三角形剪拼到下面，正好拼成一个长方形，长方形的长就是三角形的底，宽变成了高的一半，所以用底乘高除以2就是三角形的面积。”

笔者很惊讶，原来三角形和长方形有如此渊源。当然也有用两个完全一样的三角形拼成平行四边形来推导的：“我是用两个完全一样的三角形拼成一个平行四边形，平行四边形的底就是三角形的底，平行四边形的高就是三角形的高，每个三角形的面积是平行四边形面积的一半，平行四边形的面积是底乘高，三角形的面积就是底乘高除以2。”

通过这节课的探究，学生不仅掌握了三角形的面积计算方法，更增强了求异的意识，培养了学生的创造性。

挖掘探究的价值

数学教学是一种有计划、有组织的创造性活动，在数学教学中，教师提供数学素材，帮助学生衔接已有知识和经验，发展新的数学观念，建构数学。教师要准确地把握每一节课的学习内容，设计出符合学生认知规律的问题，让学生通过观察猜想、实验证明等活动寻求数学经验，充分挖掘探究内容的价值。

如教学下面的问题：

小明参观钢铁厂时看到许多钢管堆成如下图的形状。最上层有9根，最下层有16根，有8层。

大部分学生用加法计算：9+10+11+12+13+14+15+16=100（根）。这种方法学生容易理解，但是写起来比较繁琐。于是笔者故意启发学生：“瞧，它的横截面是什么形状的？”很快有学生想到了计算方法：（9+16）×8÷2=100（根）。

笔者反问学生：“怎么计算钢管的根数变成了计算横截面的面积了？”学生一脸茫然，这时，一名女生站起来说道：“如果找同样多的一堆钢管，倒过来与它拼起来，横截面就成了平行四边形。这样每层都有9+16=16（根），一共8层，所以每堆钢管就有（9+16）×8÷2=100（根）。”

笔者表扬了这位同学。这位学生又很快发现：“梯形的上底就是第一个加数，下底就是最后一个加数，高就是加数的个数。”接着我又出示了两个加法算式，要求学生用梯形面积公式计算。

9+10+11+12+13+14+15+16+17+18

1+2+3+4+5+……+15+16+17+18

其中一位学生站起来激动地说道：“我早就知道连续的自然数相加，可以用第一个数与最后一个数的和乘以自然数的个数，再除以2这种方法计算。”

这样的教学内容，加强了数学与生活的应用联系，提高了学生解决问题的能力，同时为以后的学习做好了铺垫。