双渠道销售差别定价闭环供应链协调应对生产成本扰动研究

李新然, 何 琦

(大连理工大学 管理与经济学部，辽宁 大连 116024)



双渠道销售差别定价闭环供应链协调应对生产成本扰动研究

李新然, 何 琦

(大连理工大学 管理与经济学部，辽宁 大连 116024)

针对一个新产品和再造品存在差别定价，且两类产品通过不同销售渠道进行销售的闭环供应链，构建了一个基本的两部收费契约协调模型。随后，考虑突发事件同时干扰新产品和再造品生产成本的情况下，集中式决策闭环供应链的最优决策问题，并设计了可协调成本扰动下双渠道销售差别定价闭环供应链的两部收费契约。研究表明：在集中式决策闭环供应链中，相比于稳定环境下新产品和再造品的最优决策，生产成本扰动下两类产品最优产量的调整方式不仅与生产成本扰动的程度相关，还与两类产品之间的相互替代系数相关，且改进的两部收费契约以系统各成员共担风险的方式实现了闭环供应链协调的目的。

闭环供应链；生产成本扰动；差别定价；两部收费契约；双渠道销售

0 引言

近年来，为了提高环境质量，缓解人们日益增长的物质需求同资源短缺的矛盾，实现经济与环境的可持续发展，我国相继出台了许多法律法规要求企业开展废旧品的回收再利用活动。如：2010年印发的《关于推进再制造产业发展的意见》，以及2013年通过的《中共中央关于全面深化改革若干重大问题的决定》分别为再制造产业和循环经济的发展提供了有力的政策扶持。此外，企业的废旧品再制造行为在满足市场需求和降低生产成本的同时还能提升企业的社会形象，所以包含废旧品回收再利用活动的闭环供应链管理模式受到了学术研究者和企业实践者的共同关注[1,2]。

目前，许多学者在闭环供应链的定价及契约协调方面展开了研究。Savaskan等[3]构建了由单个制造商和单个零售商构成的闭环供应链系统，通过对比分析集中式决策闭环供应链和三种回收模式下分散式决策闭环供应链的决策结果后发现，分散式决策闭环供应链中存在着的“双重边际效应”问题会使得整个闭环供应链的效益产生损失，但通过实施两部收费契约就可以对其实现有效协调；随后，Savaskan等[4]将研究扩展到两个竞争零售商的情形；邱若臻等[5]综合考虑了制造商和零售商同时负责产品回收的双回收渠道情况，建立了制造商作为主导者的闭环供应链模型，并探讨了两部收费制契约如何协调分散式决策闭环供应链的问题；Karakayli等[6]进一步考虑了制造商和第三方回收商分别作为市场领导者的情况，并采用两部收费契约分别对这两种情况下的闭环供应链进行了协调。以上研究都假设新产品和再造品具有相同的市场认可度，并享受同样的批发价格和销售价格。但在实际运营过程中，由于再制造技术水平的限制、法律法规的要求(如：我国的《废旧家电及电子产品回收处理管理条例》规定企业要对新产品和再造品进行区分)，以及人们对再造品的认识存在一定偏见等原因，新产品和再造品在销售市场上存在差别定价，且再造品的销售价格通常要低于新产品的销售价格[7,8]。基于此，包晓英等[9]运用两部收费契约协调了由单个制造商和单个零售商组成的差别定价闭环供应链系统；郑克俊[10]分别采用特许经营费用契约和收益共享契约对新产品和再造品存在差别定价的闭环供应链进行了协调。以上研究都假设新产品和再造品通过相同的销售渠道进行销售，且具有相同的市场认可度。但是，该种销售模式对新产品和再造品渠道管理难度较大，容易产生将再制造产品混同新产品销售的现象，损害企业的声誉。为了避免出现类似情况，一些企业通过不同的销售渠道以不同的销售价格销售新产品和再造品，如苹果公司将全新iMac和iPod通过零售商进行分销，而贴有“原产翻新”标识的翻新机仅通过官网分别以新产品价格12%和22%的折扣价进行销售[11]。由此可见，对双渠道销售模式的研究具有非常重要的现实意义。

此外，上述研究均建立在闭环供应链所处内外部环境均不会发生变化的假设之上，但供应链在实际运营过程中通常会遇到各类突发事件(如：自然灾害、宏观政策突变、恐怖袭击、企业运营中的突发问题(如：生产事故)等)，其会直接或间接导致供应链预测的生产成本与实际生产成本之间产生偏差，进而导致原稳定环境下的生产计划不再可行。因此，供应链成员采取何种应急管理措施应对突发事件干扰就成为产业界和学术界共同关注的重要课题。Xu等[12]在突发事件干扰生产成本的情况下，构建了由单个供应商和单个零售商组成的供应链系统，分别考虑了产品市场需求与销售价格线性相关和非线性相关的情况，并采用数量折扣契约协调对供应链进行了协调；Xiao等[13]构建了由单个制造商和两个竞争零售商组成的供应链模型，在突发事件同时干扰产品市场需求和生产成本的情况下，分别采用全单位数量折扣契约和增量单位数量折扣契约对由两个竞争零售商组成的供应链进行了协调；在此基础上，曹二保等[14]将研究扩展到由单个供应商和n个竞争零售商组成的供应链的情形，探讨了供应链面临市场需求和生产成本同时扰动时的最优应对策略问题；Huang等[15]进一步在单个制造商直销和单个零售商销售同时存在的情况下构建了双渠道供应链模型，分别研究了突发事件干扰生产成本后，分散式决策和集中式决策下供应链的生产和定价决策问题。由于闭环供应链引入了废旧品回收再制造的逆向反馈过程，其拥有比传统供应链更复杂的网络结构，所以更容易受到各类突发事件的影响。对此，王玉燕[16]探讨了产品市场需求和生产成本同时发生扰动时闭环供应链各成员的最优应对策略问题，并采用数量折扣契约对闭环供应链进行了协调；王旭等[17]研究了市场规模和再制造成本同时发生变化时，集中式决策闭环供应链的最优应对策略。但目前，许多学者仅仅对突发事件干扰下无差别定价闭环供应链的应对策略进行了研究，而鲜有考虑新产品和再造品存在差别定价且通过双渠道进行销售时闭环供应链的契约协调及应急管理问题。

因此，为了探讨双渠道销售差别闭环供应链如何采用契约协调应对突发事件干扰的问题，本文构建了由一个制造商、一个新产品零售商和一个再造品零售商所组成的双销售渠道差别定价闭环供应链模型，并逐步开展以下工作：(1)设计一个两部收费契约用以协调稳定环境下的分散式决策闭环供应链；(2)研究突发事件同时干扰新产品和再造品生产成本时，集中式决策闭环供应链的最优应对策略；(3)探讨如何改进两部收费契约以使其协调生产成本扰动下分散式决策闭环供应链的问题。

1 契约协调双渠道销售闭环供应链的基本模型

系统为由一个制造商、一个新产品零售商和一个再造品零售商所组成的双渠道销售闭环供应链；三者之间信息对称，即供应链成员完全清楚各方的成本、需求等信息；制造商和两个零售商之间存在斯坦科尔伯格博弈关系，其中制造商是领导者，两个零售商是跟随者，且两个零售商之间存在价格竞争；制造商负责回收废旧品，并同时开展利用原材料生产新产品和利用废旧品生产再造品的生产活动。

模型中的假设及符号说明如下：

(1)假设一单位的废旧品只能生产一单位的再造品，制造商根据再造品的市场需求决定废旧品的回收数量，即废旧品的回收数量和市场上再造品的销售数量相同。设制造商利用废旧品生产再造品的单位生产成本为cr，利用原材料生产新产品的单位生产成本为cn，为使制造商进行废旧品回收再制造活动有利可图，应有cn>cr>0；

(2)新产品零售商和再造品零售商分别以批发价格wn和wr从制造商处批发新产品和再造品。新产品零售商只负责销售利用原材料生产的新产品，再造品零售商只负责销售利用废旧品再加工形成的再造品，且两种产品存在差别定价；

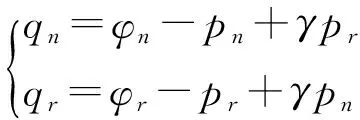
(4)制造商从消费者手中回收废旧品的单位回收价格为A，同文献[4]，假设消费者返还的产品具有较低的残值且不存在二级交易市场，因此将A设为内生变量，考虑到再制造过程的经济性，应有cr+A≤cn。

基于以上假设和符号说明，可得制造商，新产品零售商、再造品零售商以及整个闭环供应链的利润函数分别为：

πM(wn,wr)=(wn-cn)qn+(wr-cr-A)qr

(1)

(2)

(3)

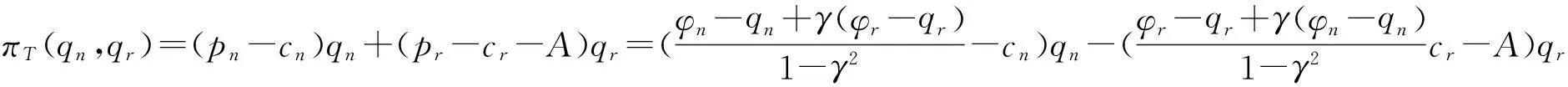
(4)

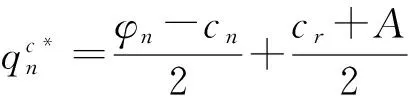
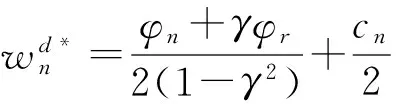
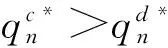
这是因为在分散式决策下，制造商和零售商均会以自身利润最大化为目标进行决策，这就会使得新产品和再造品的最优销售价格均高于集中式决策闭环供应链中两类产品的最优销售价格，进而会导致新产品和再造品的市场需求量(也即制造商的最优产量或两个零售商的最优订购量)低于集中式决策闭环供应链的市场需求量，最终使得整个分散式决策闭环供应链可获得的最优利润要少于集中式决策闭环供应链可获得的最优利润，即产生了“双重边际效应”问题。

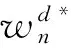
证明 在两部收费契约下，两个零售商的利润函数分别为：

(5)

(6)

式(5)对qn求一阶导，式(6)对qr求一阶导可得

(7)

对式(7)求解后可得

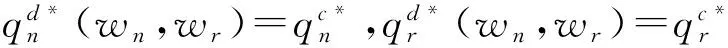
此时，制造商的利润为

新产品零售商和再造品零售商的利润函数分别为

(8)

(9)

通过式(8)和式(9)可知，制造商和零售商可通过讨价还价的方式来确定固定费用Fn和Fr的取值，以确定如何分配闭环供应链的整体最优利润。

引理1得证。

2 生产成本扰动下闭环供应链的应对策略分析

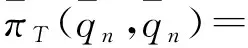
(10)

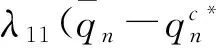
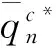
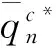
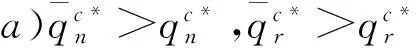
(11)

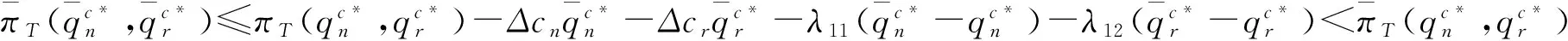
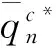
类似1)的证明可证得2)。

命题1得证。

基于命题1，有如下分析：

情况1 当Δcn≥0且Δcr≥0时，最大化集中式决策闭环供应链的利润函数可分别有如下几个有约束非线性规划问题：

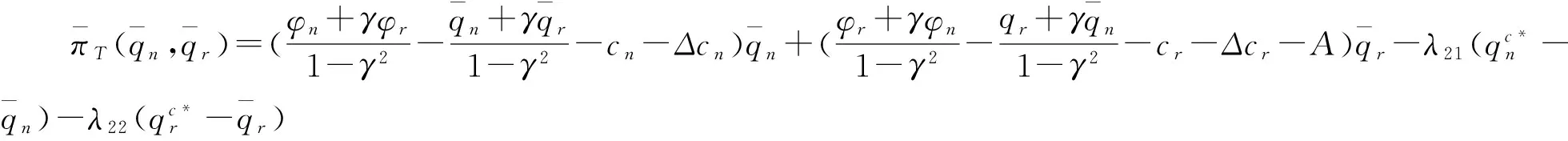
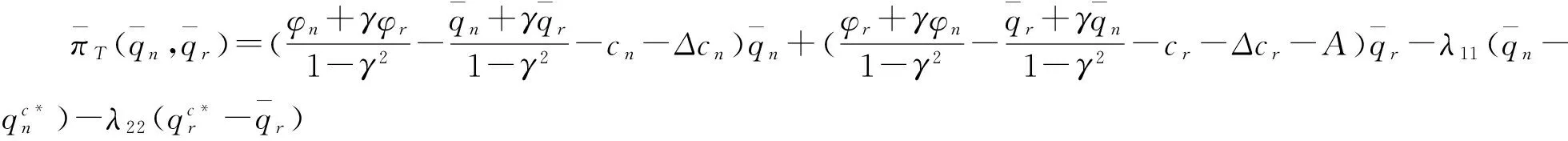
在有约束线性规划(Ⅰ)情况下，集中式决策闭环供应链的利润函数为：

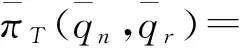
(12)

根据运筹学对二元函数凹凸性的定义，可得如下定理。

定理[18]设函数f(x,y)是定义在区域D上的二元函数，若对任意实数t∈(0,1)，及任意两点(x1,y1)∈D，(x2,y2)∈D，恒有f(tx1+(1-t)x2,ty1+(1-t)y2)>tf(x1,y1)+(1-t)f(x2,y2)，则称函数f(x,y)为定义在D上的严格凹函数。

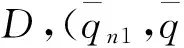
(13)

对(13)式求解可得：

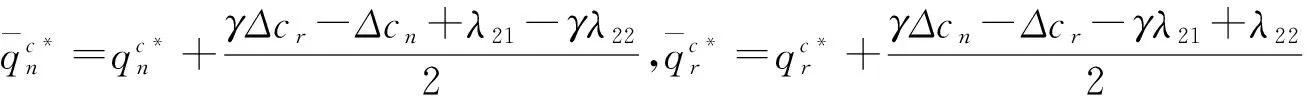
同理，可得(Ⅱ)的最优解为：

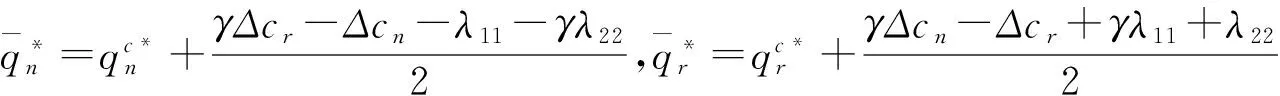
可得(Ⅲ)的最优解为：

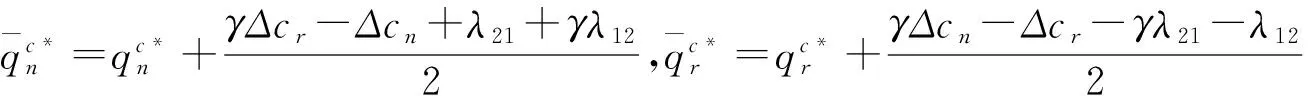
情况2 当Δcn<0且Δcr<0时，最大化集中式决策闭环供应链的利润函数可分别有如下几个有约束非线性规划问题：

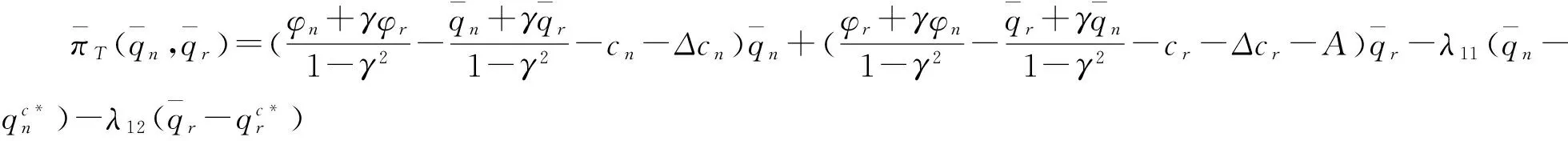
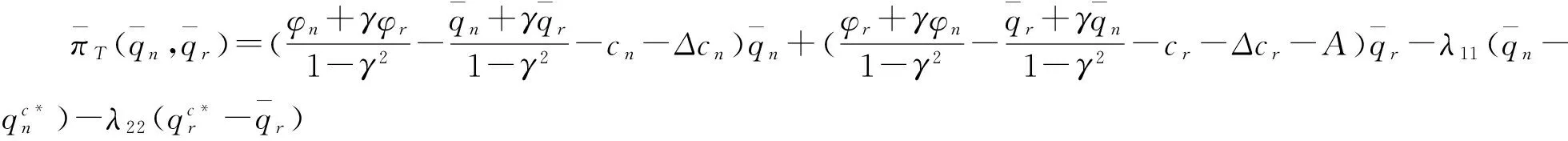
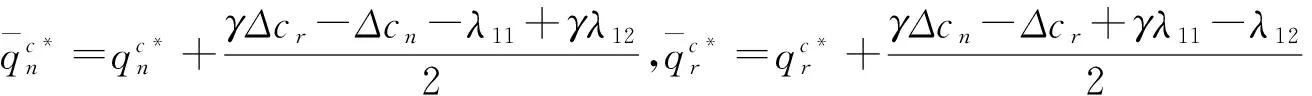
可得(Ⅴ)的最优解为：

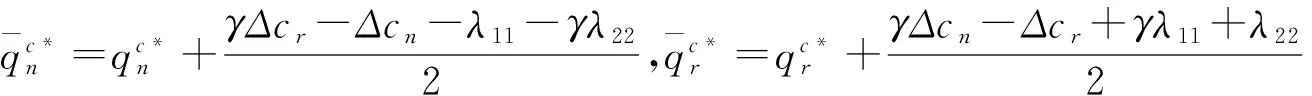
可得(Ⅵ)的最优解为：

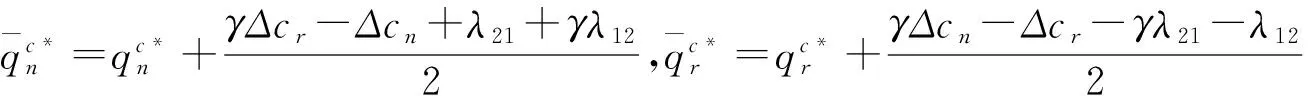
综合考虑Δcn≥0且Δcr≥0和Δcn<0且Δcr<0等两种情况下集中式决策闭环供应链的最优解，可得如下命题2。

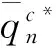
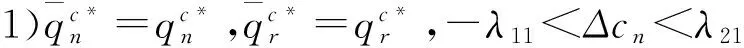
命题2表明：当突发事件使得新产品和再造品生产成本扰动的程度均不大，即情况(1)时，应保持两类产品稳定环境下的最优产量不变；当突发事件使得其中一类产品的生产成本扰动的程度很大，而使得另一类产品生产成本扰动的程度位于一定范围内(如：γΔcn-γλ21-λ12≥Δcr≥0和γΔcn-γλ21-λ12<Δcr<γΔcn-γλ21+λ22等，易知这些范围边界与受影响程度较大产品的生产成本扰动幅度，以及两类产品的替代系数呈正相关)时，对于受干扰程度很大的产品来说，应按其生产成本扰动的相反方向调整稳定环境下的最优产量，而对另一类产品来说，若发生扰动的程度相对较小，即情况(2)时，应按该类产品生产成本扰动的相同方向调整其稳定环境下的最优产量，若发生扰动的程度相对较大，即情况(3)时，应保持该类产品稳定环境下的最优产量不变；当突发事件使得两类产品生产成本扰动的程度均很大，即情况(4)时，应按这两类产品生产成本扰动的相反方向调整这两类产品稳定环境下的最优产量。

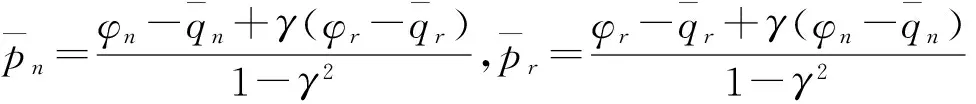
3 契约协调生产成本扰动下分散式决策闭环供应链分析

同文献[15]，在分散式决策闭环供应链中，假设突发事件所产生的额外生产或处理成本由制造商承担，所以，突发事件干扰下两个零售商的利润函数形式与其在稳定环境下的相同。

在实际运营过程中，制造商的决策会受到时间、空间以及信息反馈等的影响，但有时其并不能够及时察觉到突发事件的发生。因此，下面分析突发事件发生后，制造商仍采用原稳定环境下的两部收费契约时，分散式决策闭环供应链的协调情况。有如下命题：

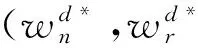
证明 突发事件发生后，若采用稳定环境下的两部收费契约，新产品零售商和再造品零售商的利润函数分别为：

(14)

(15)

(16)

(17)

命题3得证。

由命题3可知，突发事件发生后，当新产品或再造品中至少有一种产品生产成本扰动程度比较大时，需通过改进原稳定环境下的两部收费契约来协调分散式决策闭环供应链，有如下命题。

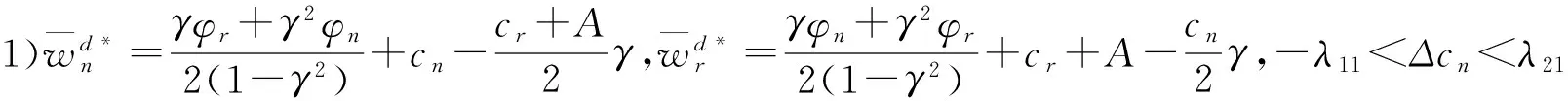
证明 当Δcn≥λ21且γΔcn-γλ21-λ12≥Δcr≥0或γΔcr+λ21+γλ12≤Δcn<0且Δcr≤-λ12时，若改进的两部收费契约满足

则新产品零售商和再造品零售的利润函数分别为：

(18)

(19)

(20)

对式(20)求解后可解得

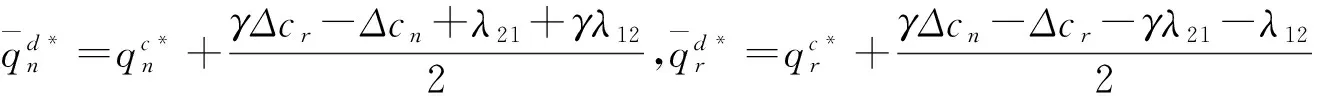
即改进的两部收费契约可协调生产成本扰动下的闭环供应链。同理可证新产品和再造品生产成本的扰动范围处于其它情况时，改进的两部收费仍能协调分散式决策闭环供应链。

命题4得证。

从命题4可以看出，在改进后的两部收费契约的协调下，制造商和两个零售商能够共同承担由于突发事件所带来的成本增加的风险，实现了分散式决策闭环供应链中各成员共同应对突发事件干扰的目的。

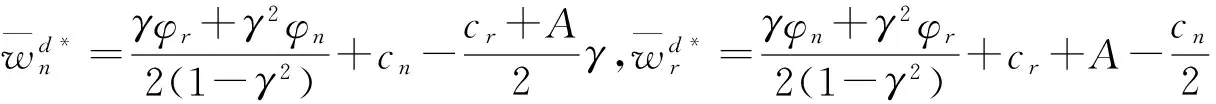
(21)

(22)

4 结论

本文以新产品和再造品存在差别定价的双渠道销售闭环供应链为对象，研究了两部收费契约协调应对突发事件干扰两类产品生产成本的问题。研究表明：两部收费契约能够协调解决闭环供应链中的“双重边际效应”问题，提高系统效益；在集中式决策闭环供应链中，当突发事件同时干扰新产品和再造品的生产成本时，两类产品在稳定环境下的最优生产计划具有一定的鲁棒性；当突发事件使得其中一类产品的生产成本扰动程度很大，而使得另一类产品的生产成本扰动程度位于一定范围内时，对于受干扰程度很大的产品来说，应与其生产成本扰动相同方向调整其稳定环境下的最优销售价格，同时反方向调整其稳定环境下的最优产量，此时，对另一种产品来说，其应对策略与受干扰很大产品的生产成本扰动程度以及两类产品的替代系数相关；当突发事件使得两类产品的生产成本扰动程度均很大时，应同时按生产成本扰动的相同方向调整两类产品稳定环境下的最优销售价格，反方向调整它们稳定环境下的最优产量。采用改进的两部收费契约，可使制造商和零售商共同承担突发事件带来的风险，同时使得突发事件干扰下双渠道销售分散式决策闭环供应链的重新实现协调。

[1] Guide J V D R, Jayaraman V, Linton, J D. Building contingency planning for closed-loop supply chains with product recovery[J]. Journal of Operations Management, 2003, 21(3): 259-279.

[2] Guide J V D R, Van Wassenhove Luk N. The evolution of closed-loop supply chain research[J]. Operations Research, 2009, 57(1): 10-18.

[3] Savaskan R C, Bhattacharya S, Wassenhove L N V. Closed-loop supply chain models with product remanufacturing[J]. Management Science, 2004, 50(2): 239-252.

[4] Savaskan R C, Wassenhove L N V. Reverse channel design: the ease of competing retailers[J]. Management Science, 2006, 52(5): 1-14.

[5] 邱若臻,黄小原.具有产品回收的闭环供应链协调模型[J].东北大学学报(自然科学版),2007,28(6):883- 886.

[6] Karakayli I, Emir-Farinas H, Akcali E. An analysis of decentralized collection and processing of end-of-life products[J]. Journal of Operations Management, 2007, 25: 1161-1183.

[7] Debo L G, Toktay L B, Van Wassenhove L N. Market segmentation and product technology selection for remanufacturable products[J]. Management Science, 2005, 51(8): 1193-1205.

[8] Ferrer G, Swaminathan J M. Managing new and differentiated remanufactured products[J]. European Journal of Operational Research, 2010, 203(2): 370-379.

[9] 包晓英,唐志英,唐小我.基于回收再制造的闭环供应链差异定价策略及协调[J].系统管理学报,2010,19(5):546-552.

[10] 郑克俊.存在价格差异的闭环供应链定价策略及契约协调[J].运筹与管理,2012,21(1):118-123.

[11] 刘勇,熊中楷.新产品分销下再制造产品直销与分销渠道研究[J].工业工程与管理,2011,16(4):40- 45.

[12] Xu M, Qi X T, Yu G, et al. Coordinating dyadic supply chains when production costs are disrupted[J]. IIE transactions, 2006, 38(9): 765-775.

[13] Xiao T J, Qi X T. Price competition, cost and demand disruptions and coordination of a supply chain with one manufacturer and two competing retailers[J]. Omega, 2008, 36(5): 741-753.

[14] 曹二保,赖明勇.需求和成本同时扰动时多零售商供应链协调[J].系统工程理论与实践,2010,(10):1753-1761.

[15] Huang S, Yang C, Liu H. Pricing and production decisions in a dual-channel supply chain when production costs are disrupted[J]. Economic Modelling, 2013, 30: 521-538.

[16] 王玉燕.需求与成本双扰动时闭环供应链的生产策略和协调策略[J].系统工程理论与实践,2013,33(5):1149-1157.

[17] 王旭,高攀,景熠.两零售商竞争的闭环供应链应对突发事件[J].计算机集成制造系统,2014,20(2):430- 439.

[18] 甘应爱,田丰,李维铮,等.运筹学[M].北京:清华大学出版社,2005:138.

Coordination of Differential Price Closed-Loop Supply Chain with Dual Sale Channels under Production Cost Disruptions

LI Xin-ran, HE Qi

(FacultyofManagementandEconomics,DalianUniversityofTechnology,Dalian116024,China)

This paper develops a two-part tariff contract model in one-manufacture-two-competitive-retailers closed-loop supply chain(CLSC)which sells new and remanufactured products by different retailers and in different prices. Then, we consider optimal decisions of centralized dual-channel differential price CLSC under the situation that the cost of new and remanufactured products is disturbed simultaneously, and improve the two-part tariff contract to coordinate the CLSC under cost disruption. The results indicate that compared with the centralized decision under normal environment, the optimal adjustment plans of new and remanufactured products are not only related to the extent of the cost disruption, but also related to the substitute coefficient of the two products. Moreover, the improved two-part tariff contract can finally coordinate the CLSC under cost disruption by sharing risks among members.

closed-loop supply chain; production cost disruption; differential price; two-part tariff contract; dual-channel sales

2013- 09-28

国家社会科学基金资助项目(14BGL063)

李新然(1963-)，男，辽宁大连人，副教授，研究方向：生产运作管理、物流与供应链管理；何琦(1989-)，女，浙江台州人，硕士研究生，研究方向：物流与供应链管理。

F272

A

1007-3221(2015)04- 0041-11