具有退化工件和工期窗口安排的排序问题
2015-07-07刘春来王建军赵传立
刘春来, 王建军, 赵传立
(1.大连理工大学 系统工程研究所,辽宁 大连 116023; 2.沈阳师范大学 数学与系统科学学院,辽宁 沈阳 110034)
具有退化工件和工期窗口安排的排序问题
刘春来1, 王建军1, 赵传立2
(1.大连理工大学 系统工程研究所,辽宁 大连 116023; 2.沈阳师范大学 数学与系统科学学院,辽宁 沈阳 110034)
针对具有退化工件的排序模型,考虑了单机排序和两台机器流水作业的工期窗口安排问题,在这一模型中,工件的加工时间是与其开工时间和退化率有关的一个线性函数。目标是找到一个最优排序和确定工期窗口的开始时间及大小以便最小化所有工件的费用函数,费用函数由四部分组成:提前、延误、工期窗口开始时间和工期窗口大小。对所研究的单机问题,详细地讨论了符合现实情况的几种类型问题,并得到了问题的最优解;对两台机器流水作业问题,给出了多项式算法。
排序;工期窗口;退化工件;提前-延误
0 引言
大量排序问题的研究中都假定工件的加工时间是固定不变的常数,但在现实的环境中,机器的效率可能由于机器使用时间的增加而降低,从而导致工件的加工时间可能随着开工时间的增加而增加,这种现象被称之为退化现象,也称为与开工时间相关的排序问题[1]。工件加工时间与其开工时间有关的排序模型在钢铁工业,塑料工业及医疗等方面都有着广泛的应用[2]。在这类模型中,工件的真实加工时间函数通常由基本加工时间、退化率和开工时间来决定。
加工时间与开工时间有关的排序问题由Gupta和Gupta[3]首先提出,他们研究了非线性加工时间极小化最大完工时间的单机排序问题,给出了一个启发式算法并进行了数值仿真;对于加工时间是线性的问题,给出了多项式算法。Browne和Yechiali[4]对有关随机变量的单机排序问题进行了研究,对目标函数为极小化最大完工时间期望和极小化最大完工时间方差的问题给出了求解最优排序的多项式算法。Mosheiov[5]考虑了具有简单线性退化的排序问题,证明了最大完工时间、加权总完工时间、最大延误、误工总数等经典正则目标函数都是多项式时间可解的。Gordon[6]等人讨论了工件的加工时间既与其在排序中的位置有关,又与其开始加工时间有关的各种常见经典目标函数的单机排序问题。Mosheiov[7]讨论了一个单机极小化总完工时间问题,证明了最优排序具有V形性质。Cheng[8]等人总结了加工时间与开工时间相关的排序问题的最新研究,同时也提出了一些尚未解决的问题。
另一方面,涉及工期窗口的排序问题也得到了深入的研究,所谓的工期窗口排序问题是指:供应商与客户商协商确定一段交货期时间窗口,使得在这段交货期时间内完工的工件不受处罚,而在这段交货期时间之前或之后(称为提早或延误)完工的工件受到相应的处罚,对于这方面的相关研究可参见文献[9~11]。有关退化工件的非正则目标函数的排序问题也是目前研究的热点。Wang[12]等人探讨了具有线性退化工件的单机排序问题,目标函数为极小化最大延迟的绝对值。对于共同工期是已给定的常量和待确定的未知变量的情况,证明了所研究的问题都是多项式时间可解的。Yang[13]等人研究了具有工件相关的老化效应和有关工期窗口的恶化维修的排序问题,目标是找到维修的最佳时间、工期窗口的开始和结束时间及其最优工件顺序以便极小化提前、延误、工期窗口的开始时间和大小的总费用,并对他们所研究的问题提出了多项式解法。Mosheiov和Sarig[14]研究一种关于工期窗口的极小最大化排序问题,讨论了单机、平行机和流水作业机三种情况,对单机问题和两台机器的流水作业问题给出了多项式解法。
绝大多数文献在研究涉及工期窗口排序问题时,都假定工件的加工时间是固定的常量或所研究的目标函数是单目标函数、提前/延误与工期窗口的加权和等规则函数。本文在文献[14]的基础上考虑具有退化工件的排序问题,对单机和两台机器流水作业问题研究了最优化所有工件最大费用(由最差排序产生的处罚)的最小值这一问题,费用函数由四个因子构成:提前、延误、工期窗口开始时间和工期窗口大小。同时,为了能够更好地反映现实情况,详细讨论了单机问题中的几种情形,分别得到了解决问题的最优策略。对于两台机器流水作业问题,通过分析最优解性质和引入Repeated-Johnson算法,得到了工件最大费用的最小值。对所研究的两个问题,证明是多项式可解的且给出了相应的多项式算法。
1 问题描述
假设N={J1,J2,……,Jn}表示需要排序的工件集,同参考文献[12]一样,我们假设所有工件在加工过程中都是不可中断的且所有的工件在时刻t0>0时都已到达,且所有的工件具有一个共同的工期窗口。如果工件Jj的开工时间为sj,退化参数为αj,那么工件Jj的实际加工时间为:pj=αjsj,j=1,2,……,n,令d1和d2分别表示工期窗口的开始和结束时间,D=d2-d1表示工期窗口的规模大小,那么显然有d2≥d1。处在工期窗口之中完工的工件称为准时工件,不进行处罚;而在工期窗口开始时间之前或结束时间之后完工的工件要进行相应的处罚。
对于一个给定排序π=(J[1],J[2],…,J[n]),定义为C[j]为位于排序中第j个位置上工件的完工时间,令C[1]=Cmin表示确定排序中第一个(即最早)工件的完工时间,C[n]=Cmax表示确定排序中最后一个(即最晚)工件的完工时间。一个工件在d1时刻或之前完工的称为提前,记为E[j],表达式为E[j]=max{0,d1-C[j]}。一个工件在d2时刻或之后完工的称为延误,记为T[j],表达式记为T[j]=max{0,C[j]-d2}。使用与文献[14]中相同的目标函数,本文的研究目标就是找到一个排序和工期窗口以便极小化以下的最大费用:
(1)
其中μ,β,γ,δ分别是提前、延误、工期窗口开始时间和工期窗口大小的单位处罚费用。
2 单机情况
2.1 工期窗口位置和大小均给定的情况

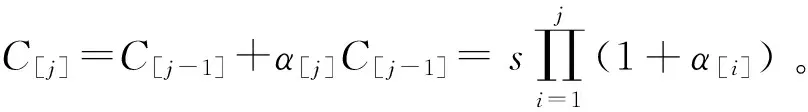
显然,在这种情况下,最优排序中相邻的加工工件之间不会有空闲空间。在一个排序中,排在第一个位置的工件决定了最大提前的大小,排在最后的工件决定最大延误的大小。当工期窗口给定时,总费用可以表示为:

(2)
定理1 对于工期窗口位置和大小给定的情况,将退化率最大的工件首先加工会得到最优排序。
证明 令αl=max{αj:j=1,2,…,n}。那么对所有j=1,2,…,n,由(2)式可得:
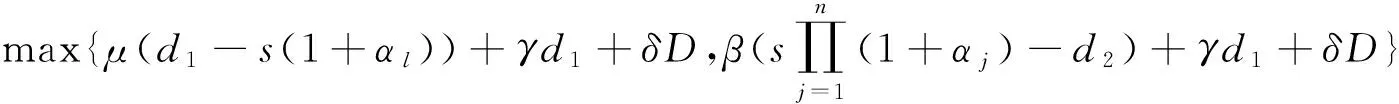
(3)
下面我们考虑四种情况:
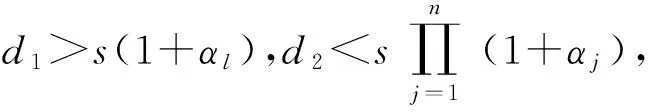
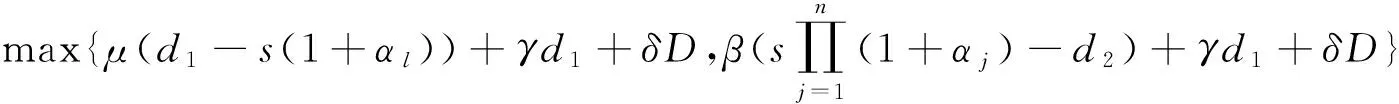
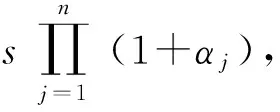
μ(d1-s(1+αl))+γd1+δD≤μ(d1-s(1+αj))+γd1+δD
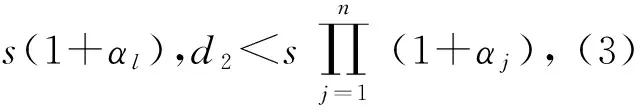

基于以上的讨论,(3)式对j=1,2,…,n都成立。证毕。
由定理1可知,总费用可以通过下式代替:
(4)
其中αl=max{αj:j=1,2,…,n}。
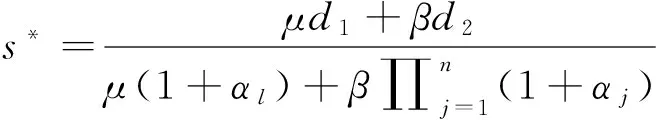
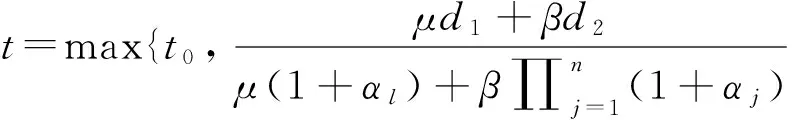
2.2 工期窗口大小给定的情况

引理2 对于一个给定的排序π=(J[1],J[2],…,J[n]),可在以下三种情况中的一种得到最优解:


证明 显然d2≤Cmax,下面考虑两种情形β≥γ和β<γ。
β≥γ的情况:继续分两种情况来考虑。如果D>Cmax-Cmin,那么有d1 Z(D)=β(Cmax-d1-D)+γd1+δD=(δ-β)D+(γ-β)Cmin+βCmin 如果D≤Cmax-Cmin,下面证明d1≥Cmin。假如d1 μ(d1-Cmin)+γd1+δD=β(Cmax-d1-D)+γd1+δD Z(D)=β(Cmax-d1-D)+γd1+δD=(δ-β)D+(γ-β)t0+βCmax,证毕。 通过以上引理2的分析,对一给定的排序,能够得到最优工期窗口的开始时间。在情形(1)中,总费用是一个常量并且与工件顺序无关。在情形(2)和(3)中,当最大化Cmin时,总费用最小,即将退化率最大的工件首先加工。 2.3 工期窗口开始时间给定的情况 引理3 对于一个给定的排序π=(J[1],J[2],…,J[n]),可在以下两种情况中的一种得到最优解: (1)工期窗口的大小为零,即D=0。 (2)工期窗口的大小为Cmax-d1,即D=Cmax-d1。 证明 将工期窗口的结束时间向右移动Δ个时间单位(工期窗口的开始时间d1不变),则总费用的改变ΔZ=Δδ-Δβ=Δ(δ-β)。如果β>δ,那么直到d2=Cmax的移动都是可行的,即D=Cmax-d1。总费用(有关d1的表达式)可表示为: Z(d1)=μ(d1-Cmin)+γd1+δD=(μ+γ-δ)d1+δCmax-μCmin 如果β≤δ,那么工期窗口的结束时间向左移将会使总费用减少。显然,总费用的改变ΔZ=Δβ-Δδ=Δ(β-δ)<0。因此,工期窗口的结束时间向左移直到d2=d1,即D=0。总费用(有关d1的表达式)可表示为: Z(d1)=max{μ(d1-Cmin)+γd1,β(Cmax-d1)+γd1},证毕。 通过以上引理3,对于一个给定的排序,能够得到最优工期窗口的结束时间。在情形(1)中,当最大化Cmin,即将退化率最大的工件首先加工时,总费用最小。在情形(2)中,最小总费用可由max{μ(d1-Cmin)+γd1,β(Cmax-d1)+γd1}得到。 因为d1-s(1+αl)≤d1-s(1+αj),所以,将退化率最大的工件首先加工能使总费用最小。 2.4 工期窗口位置和大小均是变量的情况 引理4 对于一个给定的排序π=(J[1],J[2],…,J[n]),可在以下四种情况中的一种得到最优解: 证明 可参见文献[14]中的引理1,方法类同。 通过引理4,能够得到最小费用。经过计算,情况(1)和(4)的最小费用分别为βCmax和δCmax。由于时间相关的极小化时间表长问题与工件的排列顺序无关,所以情况(1)和(4)中的最小费用与工件的排列顺序无关。对于情况(2)和(3),通过计算得最小费用分别为(μCmin(γ-β)+βCmax(μ+γ))/(μ+β)和δCmax+Cmin(γ-δ)。因为情况(2)中β≥γ,情况(3)中δ≥γ,所以,当最大化Cmin时费用最小。显然,将退化率最大的工件首先加工能够最大化Cmin。由此,提出一个算法复杂性为O(nlogn)的与文献[14]相似的算法。 算法1 如果β≥γ: 否则,退化率最大的工件在t0时开始加工; 如果β<γ: 在两台机器流水作业排序问题中,有n个工件需要加工,每个工件Jj有两道工序(T1j,T2j),j=1,2,…,n。各个工件依次在两台机器上完成两道工序,即每个工件先在机器一上加工然后在机器二上加工,工序T2j只能在工序T1j完工后才能开始。工序Tij的实际加工时间可表示为: pij(t)=αijt,i=1,2;j=1,2,…,n 其中αij表示工序Tij的退化率,t>0表示工序Tij的开工时间。 对一个给定的排序π=(J[1],J[2],…,J[n]),令C[j]=C2[j](π)表示排在第二台机器第j个位置上的工件的完工时间,相应的E[j]表示工件的提前,T[j]表示工件的延误。同时假设Cmin表示在第二台机器上第一个(最早)加工工件的完工时间,Cmax表示在第二台机器上最后一个(最晚)加工工件的完工时间。与单机问题相同,研究目标是找到一个排序和工期窗口以便极小化以下的最大费用: 引理5 对于问题F2|αijt|Cmax,最优排序可由Johnson规则得到。 证明 见文献[15]中定理5。 如果Cmin和Cmax是确定的,那么问题的求解过程与单机情况相似。因此,最优解仍然是引理4中的四种情况中的一种,且最优解与变量μ,β,γ和δ有关。 由引理4可知,对于情况(1)和(4),产生的最小费用分别为βCmax和δCmax。因此,通过引理5,极小化最大完工时间可以得到这两种情况的最小费用。另外,对情况(2)和(3),经计算最小费用分别为(μCmin(γ-β)+βCmax(μ+γ))/(μ+β)和δCmax+Cmin(γ-δ) 。由于情况(2)中β≥γ,情况(3)中δ≥γ,所以,当极小化Cmax同时极大化Cmin时,总费用最小。显然地,对不同的排序两个因素的任意一个都可能产生最优解。因此,我们使用一个策略保证得到最优排序:将n个工件中的每一个安排在第一个位置一次,这样就能得到所有可能的Cmin的值,然后通过对每种情况中剩余的n-1个工件应用Johnson算法获得最优的Cmax值。当然,对极小化最大完工时间的两台流水作业排序问题,最优排序中在第二台机器上加工的工件之间可能会出现空闲时间。因此,对于情况(2)和(3),当最大化Cmin时,将所有出现空闲时间工件向后移(避免工件之间的空闲时间)。定义一个Repeated-Johnson算法:确定第一个加工的工件(重复n个工件),对剩下的n-1个工件使用Johnson算法。基于以上的问题分析,给出如下的算法: 算法2 如果β≥γ: 如果δ≤γ,应用Johnson算法; 如果β<γ: 本文主要考虑单机和两台机器流水作业问题的共同工期窗口安排和具有退化工件的排序问题,研究了所有工件最大费用的最小值,推广了已有文献的结论,拓宽了问题的适应性。工件的实际加工时间是其开工时间和退化率的线性函数,研究的非正则函数中包含四个因子:提前、延误、工期窗口开始时间和工期窗口大小。对于单机排序问题,通过对所讨论问题的模型逐步分析,得到解决问题的最优策略和最优解;对于两台机器流水作业问题,通过设计多项式算法得到了问题的最优解。对于加工时间为更一般的与开工时间有关的函数表达式的排序问题可做进一步研究,同时,将本节研究的单机加工环境换为平行机模型则问题变成NP-难的,可做进一步详细探讨。 [1] Alidaee B, Womer N K. Scheduling with time dependent processing times: review and extensions[J]. Journal of the Operational Research Society, 1999, 7(50): 711-720. [2] Gawiejnowicz S. Time-dependent scheduling[M]. Berlin : Springer, 2008. [3] Gupta J N D, Gupta S K. Single facility scheduling with nonlinear processing times[J]. Computers and Industrial Engineering, 1988, 14(4): 387-393. [4] Browne S, Yechiali U. Scheduling deteriorating jobs on a single processing[J]. Operations Research, 1990, 38(3): 495- 498. [5] Mosheiov G. Scheduling jobs under simple linear deterioration[J]. Computers and Operations Research, 1994, 21(6): 653- 659. [6] Gordon V S, Potts C N, Strusevich V A, Whitehead J D. Single machine scheduling models with deterioration and learning: handling precedence constraints via priority generation[J]. Journal of Scheduling, 2008, 11(5): 357-370. [7] Mosheiov G. A note on scheduling deteriorating jobs[J]. Mathematical and Computer Modelling, 2005, 41(8-9): 883- 886. [8] Cheng T C E, Ding Q, Lin B M T. A concise survey of scheduling with time-dependent processing times[J]. European Journal of Operational Research, 2004, 152 (1): 1-13. [9] Cheng T C E. Optimal common due-date with limited completion time deviation[J]. Computers and Operations Research, 1988, 15(2): 91-96. [10] Liman S D, Panwalker S S, Thongmee S. Common due window size and location determination in a single machine scheduling problem[J]. Journal of the Operational Research Society, 1998, 49(9): 1007-1010. [11] Mosheiov G, Sarig A. A due-window assignment problem with position-dependent processing times[J]. Journal of the Operational Research Society, 2008, 59(7): 997-1003. [12] Wang J B, Yang D L, Hsu C J. Single-machine scheduling to minimize absolute value in maximum lateness with deteriorating jobs[J]. Advanced Materials Research, 2011, 201-203: 1054-1060. [13] Yang S J, Yang D L, Cheng T C E. Single-machine due-window assignment and scheduling with job-dependent aging effects and deteriorating maintenance[J]. Computers and Operations Research, 2010, 37(8): 1510-1514. [14] Mosheiov G, Sarig A. Minmax scheduling problems with a common due-window[J]. Computers and Operations Research, 2009, 36(6): 1886-1892. [15] Zhao C L, Zhang Q L, Tang H Y. Scheduling problems under linear deterioration[J]. Acta Automatica Sinica, 2003, 29(4): 530-535. Common Due-window Assignment and Scheduling Problems with Deteriorating Jobs LIU Chun-lai1, WANG Jian-jun1, ZHAO Chuan-li2 (1.InstituteofSystemsEngineering,DalianUniversityofTechnology,Dalian116023,China; 2.SchoolofMathematicsandSystemsScience,ShenyangNormalUniversity,Shenyang110034,China) This paper is devoted to a scheduling problem with simple linear deterioration, that is, the processing time of a job is a simple linear function of its starting time and its deterioration rate. We consider the common due-window assignment problem for the single machine and two machine flow shop. The goal is to schedule the jobs and the due-window so as to minimize the highest cost among all the jobs. The objective function contains four cost components: earliness, tardiness, due-window starting time and size. By analyzing the properties of the optimal schedule, we obtain the due-window starting time and size. For the single machine and two-machine flow shop problems, we present a polynomial time solution respectively. Moreover, some special cases of the single machine are also discussed in detail. scheduling; due-window assignment; deteriorating jobs; earliness-tardiness 2013-11-09 国家自然科学基金资助项目(71271039;70902033);教育部“新世纪优秀人才支持计划”项目(NCET-13- 0082);中央高校基本科研业务费专项资金资助项目(DUT14YQ211) 刘春来(1986-),男,博士研究生,研究方向:排序理论与算法,干扰管理;王建军(1977-),男,副教授,博士,研究方向:干扰管理、电子商务与物流管理;赵传立(1958-),男,教授,博士,研究方向:组合最优化。 O223 A 1007-3221(2015)04- 0116- 06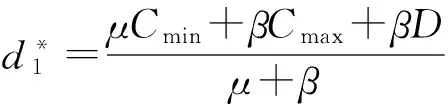

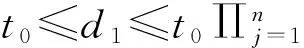


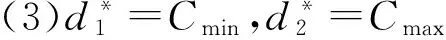

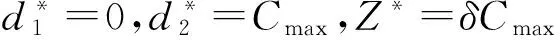
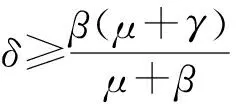
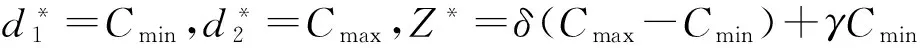
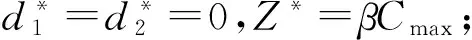
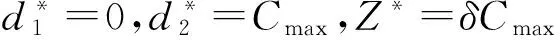
3 两台机器流水作业问题
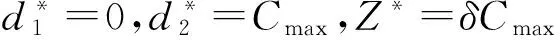
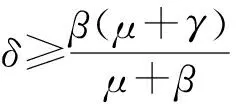
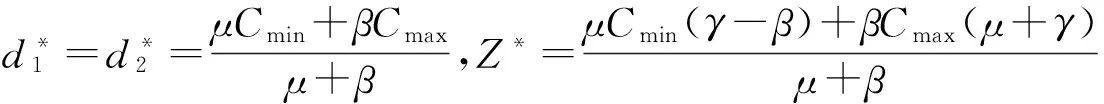
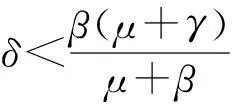
4 结论
