基于固定序的Bellman-Ford算法的改进
2015-07-07韩伟一
韩伟一
(哈尔滨工业大学 经济与管理学院,黑龙江 哈尔滨 150001)
基于固定序的Bellman-Ford算法的改进
韩伟一
(哈尔滨工业大学 经济与管理学院,黑龙江 哈尔滨 150001)
固定序算法是Bellman-Ford算法的一种基本改进算法。为了改变固定序算法在稀疏图上的劣势,本文通过预先订制参与迭代的点的计算顺序,对该算法进行了改进。实验表明,在稀疏图上, 改进后的算法相对于原算法计算效率提高了近50%, 并能够与国际流行的先进先出算法相媲美。本文的工作表明,固定序算法不仅在大规模稠密图上具有明显的优势,而且在稀疏图上也具有很强的竞争力。
运筹学;固定序改进算法;最短路序;拓扑序Bellman-Ford算法
0 引言
Bellman-Ford算法是解决负权最短路问题公认的最好算法之一[4,5,10,13], 自1958年提出以来, 共经历了三个发展阶段[1~3]:第一阶段,动态规划模式阶段, 即原始的Bellman-Ford算法;第二阶段,基本改进阶段,在第一阶段的每次迭代中所有点都要参与计算,而在第二阶段中只有在上次迭代中距离标号改变的点才参与下一次迭代, 从而使得计算效率显著提高, 迭代次数明显减少;第三阶段,加速技术阶段,主要体现为上次迭代中距离标号改变的点并不全部参与下一轮迭代计算,因而还可进一步提高计算效率。第三阶段的算法一般以第二阶段的算法为基础,因而第二阶段的算法也称为Bellman-Ford算法的基本改进算法。目前, 主要有5类基本改进算法, 即先进先出算法[10~14]、后进先出算法[14]、Yen算法[8]、快速算法[9]和固定序算法[1,2]等。第三阶段的主要工作有1993年Goldberg和Radzik两人提出的拓扑序技术[6],Tarjan于1981年提出的装配子树技术[7],以及1985年Glover等人提出的门槛技术等[4,5], 1996年Cherkassky等人提出的父点技术[10,14]等。文献[2]提出的固定序算法是一种基本改进算法,它的特点是每次迭代过程中参与计算的点总遵照固定的顺序。由于每一次迭代参与的点和点数是不确定的,因而主流的算法采用了先进先出的顺序,即距离标号先改变的点先参与迭代计算,本文称之为先进先出算法(FIFO Algorithm)。先进先出算法是当前最具影响力的一种基本改进算法。鉴于基本改进算法是第三阶段算法的基础,本文将开展两方面的工作:(1)通过实验说明固定序算法在稠密图上有明显的竞争优势; (2) 借鉴拓扑序技术对固定序算法作进一步的改进, 并通过实验说明该算法在稀疏图上能够与先进先出算法相媲美。
1 固定序算法及其实验性能
对于一个具有n个点、m条边的有向图G(V,E),n个点分别编号以1, 2, …,n,且规定点1为始点,用w(i,j)表示有向边(i,j)的权。定义d(i)为点的距离标号,k为算法的迭代次数,则固定序算法如下:
Step 1 初始化。令d(1)=0,d(i)=+∞(2≤i≤n),把点1加入集合A。k表示迭代次数,赋初值为1。
Step 2 在第k次迭代中,按照编号顺序对A中的各点i进行如下计算
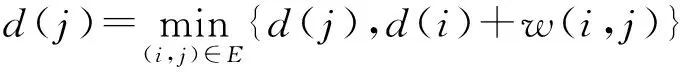
如果d(j)变小,则当j∉A时, 把点j加入集合A。从集合A中去除点i。
Step 3 如果集合A为空集,则算法结束,d(i)就是从点1到点i的最短距离;当集合A非空,且k=n-1时,可判定存在负循环,算法结束;当集合A非空时,且k Step 4 令k=k+1,转到Step 2。 在第一阶段,采用固定序是非常自然的,在第二阶段采用固定序是不明智的,原因有两点:(1)它需要把参与迭代计算的点按既定顺序进行排序,增加了额外的计算时间;(2)一成不变的计算顺序使得算法缺乏灵活性,可能会导致算法的低效率。因而,在第二阶段和第三阶段固定序算法鲜有文献提及。为了克服这一缺点,我们使用了一种简单的技术,即对所有点按给定的顺序逐个检查,如果距离标号改变了就参与计算,否则就不参与,这样可保证参与迭代点的顺序,但增加了距离标号未改变的点的检查工作。然而,这种理论上显得较弱的算法,在使用邻接矩阵的数据结构时,却极具有竞争力,在稠密图上, 它比主流的先进先出算法具有更加卓越的计算效率。为了验证这一优势,本文通过实验对两个算法进行了比较。在实验中,两种算法都选择了各自最有利的数据结构,先进先出算法使用压缩邻接表(也称为邻接顺序表),固定序算法使用邻接矩阵。同时,选择了6000点、8000点和10000点三种规模下的4种不同稀疏程度进行实验。沿用文献[2]的定义,用边数与点数之比来表示图的稀疏程度。实验用的有向图的权重服从均匀分布,可取1到100000之间的任一整数。为了保证实验结果的可靠性,每种情形将实验10000个例子。所用的计算机为联想ThinkPad笔记本,CPU为Intel i5-2410M 2.30GHz, 内存为2.0G。算法的比较都使用相同的例子。算法程序均采用结构化语言Pascal。相关的实验结果,见表1、表2和表3: 表1 10000个点下固定序算法与先进先出序算法的比较 由表1、表2和表3可以看出,在点数相同的情况下,先进先出的算法随着稀疏程度的降低计算时间不断下降, 而固定序算法的计算时间变化幅度不大, 竟然会出现不降反升的现象。之所以出现如上现象, 根本原因在于固定序算法采用的数据结构为邻接矩阵, 而先进先出算法采用的数据结构为压缩邻接表,邻接矩阵将使所有问题只能以完全图的形式参与计算,也就是两点i和j之间如果无边存在,则添加边(i,j), 且令权重为+∞,最终把一个非完全图构造为完全图。另外,由于所计算的问题均是随机形成的,因而出现不降反升的现象是正常的,但两个算法的计算时间比所体现的关系却是相对稳定的。 表2 8000个点下固定序算法与先进先出序算法的比较 表3 6000个点下固定序算法与先进先出序算法的比较 综合表1、表2和表3的实验结果,可得出如下几点结论:(1)在稠密图上,固定序算法确实比主流的先进先出序算法有明显的竞争优势;(2)固定序算法的竞争优势将随着点数规模的增加和稀疏程度的增大愈加明显, 在6000个点的完全图上, 固定序算法仅比先进先出序算法快1.3倍, 而在10000个点的完全图上效率提高了40%;(3)固定序的计算效率,还将随着稀疏程度的增大愈加显著,在10000个点的规模下,稀疏程度为7000时, 固定序算法的计算效率稍弱于先进先出算法,但当稀疏程度增加到7500时, 情况就有了明显改观;(4)固定序的优势范围将随着点数规模的增加而进一步扩大,在6000个点时,稀疏程度达到点数的5/6, 固定序算法才可以胜过先进先出算法, 但当规模升到10000个点时, 稀疏程度只需达到点数的3/4就可以。 尽管固定序算法在稠密图上显示出了明显的竞争优势,但也存在明显的劣势:(1)它的竞争优势得益于所采用的数据结构——邻接矩阵,而压缩邻接表是稀疏图上最常用、最有竞争力的数据结构;(2)固定序算法在稀疏图上不具有优势,后文表4~6的实验结果已经表明,两个算法都采用压缩邻接表的数据结构,在规模为10000个点、稀疏程度分别为5、10、15和20时,先进先出算法比固定序算法计算效率大约快50%。 为了改变固定序算法在稀疏图上的劣势,可从两方面对算法进行改进:第一,对参与迭代的点的顺序进行预先订制;第二,在算法的初始化阶段, 对参与迭代的点进行排序。第一个改进有一定的现实依据,因为计算工作都是把预先处理好的数据交给算法的。然而,预先排序会增加额外的计算时间,无法真实体现一个算法的真实竞争力,因而第二个改进更加合理一点。算法的改进也采用压缩邻接表的数据结构。 之所以改进参与迭代的点的顺序,其理论来源来自于拓扑序。拓扑序是针对无循环的有向图提出的,指对各点进行排序后,如果点i的位置先于点j,那么有向图中一定不存在边(j,i)。关于拓扑序有如下的定理: 定理1 如果图G(V,E)为无循环的有向图,那么Bellman-Ford算法第二阶段及以后的各种改进算法如果按照拓扑序对各点进行迭代计算,算法可以在O(m)的时间内获得从源点到各点的最短路径,而且仅需迭代一次。 遗憾的是,有循环的有向图却不存在拓扑序,只有无循环的有向图才存在拓扑序。值得指出的是,Bellman-Ford算法及其改进算法的计算结果将得到最短路径树,而最短路径树是无循环的有向图。为了方便论述,本文提出如下定义: 定义1 最短路径树是有向图的特殊子图,由它得到的拓扑序特称为最短路序。 显然,最短路序是拓扑序概念的一个推广,不仅无循环的有向图存在最短路序,而且有循环的有向图也存在最短路序。关于最短路序,也有如下定理: 定理2 如果图G(V,E)为有向图,那么固定序算法按照最短路序对各点进行迭代计算,算法可以在O(m)的时间内获得从源点到各点的最短路径,而且仅需迭代一次。 证明 如果P是从始点1到点t的最短路径,即1→t1→t2→…→tk→t,为了方便论述,用t0来表示点1, 用tk+1来表示点t。如果按照最短路序进行计算,那么点ts必定先于点ts+1参与计算。根据固定序算法的Step 2,在第一次迭代中,ts(0≤s≤k)将使得ts+1进入集合A, 这样不仅保证了参与计算的顺序,还同时保证了ts和ts+1都能参与计算,而计算结果又使得d(ts+1)=d(ts)+w(ts,ts+1),这意味着经过第一轮迭代就可求得从点1到点t的最短路径。鉴于点t的任意性,因而在第一轮迭代中,所有点都参与了迭代计算,并且都得到了最短路。因为每个点仅参与迭代计算一次,因而每边最多只能参加一次迭代,故算法的复杂性为O(m)。命题得证。 定理2很容易推广到Bellman-Ford算法第二阶段及以后的其它改进算法上。尽管最短路序有如此优良的理论性质,但事先很难预知,只能合理加以借鉴。既然事先很难得到最短路序,可以考虑近似最短路序,保证尽量多的点满足最短路序,同时允许部分点不满足最短路序。在近似最短路序中,无疑满足最短路序的点越多,算法的效率自然就越高。根据这个想法,可对固定序算法改进如下: Step 1 初始化。令d(1)=0,d(i)=+∞(2≤i≤n),把点1加入集合A,同时订制近似最短路序的第一个点,即点1。k表示迭代次数,赋初值为1。 Step 2 在第1次迭代中,按照订制的顺序对中的各点进行如下计算 如果d(j)变小,则当j∉A时, 把点j加入集合A。若d(j)变小且原值为+∞,设最短路序中已有t个点,那么就把点j作为第t+1个点。当所有进入A的点都参与计算后,则转入步骤Step 4。 Step 3 在第k(k≥2)次迭代中,按照订制的顺序对A中的各点i进行如下计算 如果d(j)变小,则当j∉A时, 把点j加入集合A。从集合A中去除点i。 Step 4 如果集合A为空集,则算法结束,d(i)就是从点1到点i的最短距离;当集合A非空,且k=n-1时,可判定存在负循环,算法结束;当集合A非空,且k Step 5 令k=k+1,转到Step 3。 尽管步骤Step 2对点进行排序的工作稍显简单,但却体现出了较高的计算效率,采用较复杂的技巧反而会减慢计算速度,究其原因在于参与迭代计算的点数尽管减少了,但额外增加了更多的排序时间。 为了测试改进后的算法效率,特选择了压缩邻接表, 这个最为常用的数据结构对固定序算法来说是最不利的,但对于先进先出算法来说却是最有利的数据结构。实验分别选择了6000点、8000点和10000点三种规模下的4种不同稀疏程度,选择了先进先出算法和原始的固定序算法进行比较,仍采用前文的实验方法。相关的实验结果,见表4、表5和表6: 表4 6000个点下改进固定序算法的绩效实验 表5 8000个点下改进固定序算法的绩效实验 表6 10000个点下改进固定序算法的绩效实验 综合表4、表5和表6的实验结果,可得出如下几点结论:(1)在稀疏程度小于10时,改进后的固定序算法已经略胜于先进先出算法;(2)当稀疏程度大于10时,竞争优势被先进先出算法所取代,而且随着稀疏程度的增大计算优势将逐步丧失;(3)改进后的固定序算法相对于原算法,效率有了显著提高,大约提高了近50%。鉴于现实中所面临的图绝大多数为稀疏程度小于10的稀疏图,因而改进后的固定序算法在稀疏图上是一种真正具有竞争力的算法。 尽管改进后的固定序算法在稀疏程度不大于10的有向图上有竞争优势,但本文的实验表明:在采用压缩邻接表的数据结构时,随着稀疏程度的增大,固定序算法及其改进算法劣势将渐趋明显。 本文主要有三方面的贡献:(1)验证了固定序算法在稠密图上的优势,同时对该算法的优势范围进行了实验评估;(2)拓展了拓扑序的概念,提出了最短路序这个适应性更强的新概念;(3)通过预先订制参与迭代点的顺序,改进了固定序算法。改进后的算法能极大地提高固定序算法在稀疏图上的计算效率,可提高大约50%。相对于国际流行的先进先出算法,改进后的固定序算法在稀疏程度不大于10的有向图上也取得了竞争优势,这使得固定序算法可成为解决实际问题有竞争力的算法。 在Bellman-Ford算法发展的第二阶段,固定序算法很少引起国际学术界的重视。本文对这个算法的优势重新进行了挖掘,使之既可在大规模稠密图上有较大范围的竞争优势,又可在稀疏程度小于20的稀疏图上与国际流行的先进先出算法相媲美。如何进一步改进固定序算法,使之采用压缩邻接表的数据结构能获得更大范围的竞争优势,使之在更多新领域具有无可比拟的竞争优势,将作为下一步的研究工作。 [1] 韩伟一,王铮.负权最短路问题的新算法[J].运筹学学报,2007,11(1):111-120. [2] 韩伟一.经典Bellman-Ford算法的改进及其实验评估[J].哈尔滨工业大学学报,2012,44(7):74-77. [3] Bellman R E. On a routing problem[J]. Quarterly of applied mathematics, 1958, 16(1): 87-90. [4] Glover F, Klingman D, Phillips N V. A new polynomially bounded shortest path algorithm[J]. Operations research,1985, 33(1): 65-72. [5] Glover F, Klingman D, Phillips N V, Schneider R F. New polynomial shortest path algorithms and its computational attributes[J]. Management science, 1986, 31: 1106-1128. [6] Goldberg A V, Radzik T. A heuristic improvement of the bellman-ford algorithm[J]. Applied Mathematics letters,1993, 6(3): 3- 6. [7] Tarjan R E. Shortest paths[R]. AT&T Bell Laboratories, Murray Hill, 1981. [8] Yen J Y. An algorithm for finding shortest routes from all source nodes to a given destination in general networks[J]. Quarterly of applied mathematics, 1970, 27: 526-530. [9] 段凡丁.关于最短路径的SPFA快速算法[J].西南交通大学学报,1994,29(2):202-212. [10] Cherkassky B V, Georgiadis L, Goldberg A V, Tarjan R E, Werneck R F. Shortest-path feasibility algorithm: an experimental evaluation[J]. ACM Journal of experimental algorithmics, 2009, 14(2.7): 1-37. [11] Hung M S, Divoky J J. A computational study of efficient shortest path algorithms[J]. Computer & Operations research, 1988, 15(6): 567-576. [12] Lewanddowski S. Shortest paths and negative cycle detection in graphs with negative weights[R]. Stuttgart University, 2010. [13] Cherkassky B V, Goldberg A V. Negative-cycle detection algorithm[J]. Mathematical programming, 1999, 85: 277-311. [14] Cherkassky B V, Goldberg A V. Shortest paths algorithms: theory and experimental evaluation[J]. Mathematical programming, 1996, 73: 129-174. Improvement of Bellman-Ford Algorithm Based on the Fixed Order HAN Wei-yi (SchoolofEconomicandManagement,HarbinInstituteofTechnology,Harbin150001,China) The fixed order algorithm is one of basic improved algorithms on the classic Bellman-Ford algorithm. In view of its inferiority in the sparse directed graph, the algorithm is improved by presenting the computational order of vertices in advance. The experiments show that the improved algorithm is faster than the original one by 50% in the sparse directed graph approximately. Moreover, it is compared with the FIFO algorithm, which is the most attractive basic improved algorithm of Bellman-Ford algorithm at present. It means that the fixed order algorithm is very competitive in both the large-scale dense directed graph and the sparse directed graph. operations research; improved fixed order algorithm; the shortest path order; topological order; bellman-ford algorithm 2013- 06-27 国家自然科学基金资助项目(71101037);中央高校基本科研业务费专项资金资助(HIT.HSS.201406) 韩伟一(1974-),男,讲师,硕士生导师。 O221.7 A 1007-3221(2015)04- 0111- 05


2 固定序算法的改进
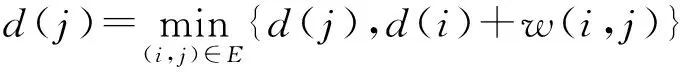
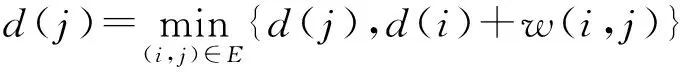
3 实验测试



4 结论
