信息与计算科学专业《数学分析》课程教学探讨

陈素根，余桂东

(安庆师范学院 数学与计算科学学院，安徽 安庆 246133)

信息与计算科学专业《数学分析》课程教学探讨

陈素根，余桂东

(安庆师范学院 数学与计算科学学院，安徽 安庆 246133)

针对我校信息与计算科学专业的特点及数学分析课程的教学现状，结合长期在数学分析教学过程中遇到的各种问题，结合教学内容选择、教学方法改进以及专业特点等方面谈几点教学体会，以提高教学质量和教学水平。

数学分析；教学效果；教学思考

随着信息技术的发展，高等教育改革的不断深化，传统数学分析教学面临新的挑战，而数学分析始终是数学学科最重要的基础课之一，在所学专业课程中，其授课周期最长，所占学时最多，它是几乎所有后继课程的基石，在培养具有良好的数学素养的专业人才方面起着非常重要的作用，其教学水平在很大程度上代表了数学基础课的水平，因此，如何提高数学分析教学质量一直是许多教学人员关注的热点问题[1-6]。

信息与计算科学专业是我院的非师范类专业之一，培养目标是以信息技术和计算技术的数学基础为研究对象的理科专业，培养具有良好的数学基础知识和数学思维能力，掌握信息与计算科学的基础理论、方法与技能，能在科技、教育、信息产业、经济金融等部门从事研究、教学、应用开发和管理工作，能继续深造。我院信息与计算科学专业开设3个学期的数学分析课程，一直非常重视数学分析的教学质量。然而，从历年的考试来看，这个专业的数学分析考试成绩比应用数学专业的要差很多，而且两极分化非常严重。经过广泛调研与交流发现，数学分析课程在该专业教学中主要存在以下一些问题：第一，教学内容不太合理；第二，教学方法相对陈旧；第三，专业结合不够紧密。

1 教学细节探讨

信息与计算科学专业虽然是数学学院的一个专业，但它毕竟不等同于数学与应用数学专业，如果按照数学与应用数学专业的要求，统一教材、统一教学和统一考核，这样来安排教学是不合理的。所以，信息与计算科学专业的数学分析课程教学不能完全与数学与应用数学专业的相同，对于教材的选择可以简单一点或者对教材内容上进行精选，保证学生可以学到相应的数学分析知识，掌握基本的数学计算技能。同时，在教学方式方法上也应该有所改进，让学生充分参与到教学过程中来，激发他们学习数学分析的兴趣和积极性。

1.1 基本概念讲解要透彻

数学分析很多概念是比较抽象和难以理解的，在批改作业以及辅导时学生询问的问题中发现，很多学生对基本概念的理解是不够清楚的，这样对课程的教学带来了很多的困难，所以注重基本概念的讲解十分必要。为了可以更好的帮助学生理解基本概念，这就需要教师尝试一些不同的讲解思路或理解方式。下面仅以几个基本概念为例进行阐述。

例1 上下确界的定义。如η=supS，即满足(1)η是S的上界；(2)η是S的最小的上界。

很多学生很难理解最小的上界的概念，所以采取两种办法来解释：第一，对任何的α<η，存在x0∈S，使得x0>α的上界；第二，对任何的ε>0，存在x0∈S，使得x0>η-ε的上界。在讲解的同时，需要举例来说明，强调要通过解不等式或实数的稠密性等手段找到具体x0满足条件才可以。

例2 极限的定义。

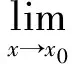
1.2 例题选择要典型

在基本概念清楚的前提下，选择适当的例题，一方面可以帮助理解基本概念，另一方面可以帮助学生将知识点进行串联起来。例题的选取要具有代表性和综合性，例题的讲解在于精，而不在于多。比如，针对一致连续性、一致收敛性和归结原则等问题，可以选取下面的例题。

在以上几个例子中，例3可以很好地解释连续与一致连续的概念及它们之间的联系与区别；例4可以很好地解释一致收敛与不一致收敛的概念之间微妙关系；例5可以用归结原则和迫敛性处理，也可以用罗必塔法则和归结原则处理。这样好的例子在数学分析教学中应多加使用，能够帮助学生在理解基本概念的同时感受到数学分析奥妙，有利于提高教学效果。

1.3 习题课的作用要重视

数学分析虽然注重于理论教学，但计算能力的提高也是必不可少的，而且良好的计算基本功对理论学习有一定的促进作用。这样，在教学过程中为时不多的习题课就显得非常重要，合理安排好习题课对正常的教学起到很好的辅助作用。根据教学的需要，将习题课分为不同的类型，以便实现不同的效果：第一，计算强化型习题课，如数列极限、函数极限、导数、定积分、不定积分、重积分、曲线曲面积分的计算，对于这一类型的习题课主要目标是巩固学生对基本公式的记忆与理解以及计算速度和准确性；第二，知识点或方法与技巧归纳与总结型习题课，如极限的24种定义的描述、函数极限的不同计算方法(定义、等价无穷小代换、罗必塔法则、泰勒公式等)、级数的敛散性判定方法，对于这一类型的习题课主要目标是提高学生对知识点的总体掌握水平，培养学生善于总结的习惯；第三，理论探讨与研究型习题课，如一致连续与一致收敛的关系、微分中值定理的推广及应用、实数完备性定理等价性证明、积分计算中对称性问题，对于这一类型习题课主要目标是强化学生分析、研究及解决问题的能力。在习题课教学安排中，尽可能让学生积极参与，鼓励学生积极查阅资料，归纳总结各种方法，广泛交流讨论。总之，通过合理安排多样化的习题课，激发学生学习的主动性，敢于面对与处理难题，起到巩固基础、提高计算能力、培养数学思维能力的作用。

1.4 反例在教学中的作用要强调

数学分析的许多概念是高度抽象、难以理解的，但有时通过引入反例教学会起到意想不到的效果[7]。对学生概念的理解和理论的建立都有很好的帮助，但是，举反例往往是比较困难的事，所以要注重平时的积累，下面的几个例子在教学过程中可以经常用到。

例7 数列an=(-1)n，可以说明数列有界仅是极限收敛的必要条件。

例9 Weierstrass反例和Van der Waerden反例，给出了处处连续但处处不可导的例子，可以说明连续是可导的必要条件。

经典反例的构造往往是比较困难的，所以这也可以鼓励学生积极参与，鼓励他们自己构造反例或者查阅资料进行收集，并在全班交流分享。

2 结合专业特点，发挥Matlab软件功能

考虑到信息与计算科学专业的专业特点，教学过程中可以适当引入一点数值分析、计算机程序设计、计算机图形学等学科的知识进行交叉教学，可以充分发挥学生的动手编程能力，让学生感觉到数学分析的实用性，如在介绍微分与泰勒公式的近似计算时，可以结合数值分析中的插值误差来教学；在讲解根的存在性定理时可结合计算机程序设计中二分法、图形学中裁剪算法或求交算法来进行。同时，可以借助Matlab软件绘制数学分析教材中学生难以理解的曲线和曲面图形，让学生有直观的感受，便于理解和掌握。

3 结束语

数学分析是数学及相关专业的基础课程，该课程不仅是后续很多课程的基础，而且是数学专业硕士研究生入学考试的必考课程之一，其教学内容都是比较经典的东西，所以，作为一名数学分析的授课教师必须时刻注重自身素质的提高，如何让该课程教学焕发新的生机是每一位教师值得思考的问题。可以从以下几个方面改进：

(1)以数学的统一性为指导思想，增加新内容，并重视现代数学语言与符号的使用，让学生在今后的学习过程中可以更好地适应；

(2)在重视理论的同时应突出应用、重视计算。数学的实际应用和数值计算是分不开的，应该跳出传统的局限于几何、物理的应用范围，教学过程中可以介绍一些经济学、运筹学、统计学、图形学等方面的应用；

(3)体现各数学分支的相互联系与渗透，教学过程中应该将数学分析、高等代数、解析几何的思想方法结合起来，让学生的学习更加体系化；

(4)结合专业特点，充分发挥各自优势，真正让理论与实践完美结合，体现数学在自然科学中的重要性和无穷魅力。

[1] 李家雄. 信息与计算科学专业《数学分析》教学探索与实践[J]. 长江大学学报(自然科学版),2011, 2(8): 129-131.

[2] 杜超雄. 在数学分析教学中打造开放性与实践性教学课堂[J]. 邵阳学院学报(自然科学版),2011, 1(8): 23-25.

[3] 张婧. 高等师范院校数学分析习题课教学探讨[J]. 太原大学教育学院学报, 2012, 30(2): 89-91.

[4] 葛仁福. 基于研究性学习的数学分析教学实践[J]. 数学教育学报, 2013, 22(1): 80-82.

[5] 盛兴平, 王海坤. 新课标下高师数学分析教学实践与研究[J]. 大学数学, 2013, 29(1): 11-14.

[6] 刘雪英. 《数学分析》课程教学方法改革的思考[J]. 内蒙古师范大学学报(教育科学版),2013, 26(1):126-128.

[7] 王宏仁, 陈鲲. 反例在数学分析教学中的应用[J]. 廊坊师范学院学报(自然科学版),2011, 1(11): 115-116.

[8] 邓宇龙. 基于Matlab的数学分析极限概念教学实践[J]. 大学数学, 2014, 30(1): 117-120.

Discussion on Teaching of Mathematical Analysis about the Major of Information and Computational Science

CHEN Su-gen，YU Gui-dong

(School of Mathematics & Computational Science, Anqing Teachers College, Anqing 246133, China)

According to the characteristics of the major of information and computation science and the teaching status about mathematical analysis course in our school, as well as various problems encountered in the process of teaching mathematical analysis, in this paper, some experience from teaching content selection, teaching methods improvement, major characteristics combination and other aspects are discussed, for the purpose of improving teaching quality and teaching level.

mathematical analysis, teaching effect, teaching thinking

2014-03-08

安徽省高等教育振兴计划(2013zdjy117)和安徽省教研项目(2012 jyxm364)。

陈素根，男，安徽当涂人，博士生，安庆师范学院数学与计算科学学院副教授，研究方向为计算机辅助几何设计与图形学、模式识别与智能系统。

时间：2016-1-5 13:01 网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160105.1301.033.html

O172/G642

A

1007-4260(2015)04-0128-04

10.13757/j.cnki.cn34-1150/n.2015.04.033