高等数学中定积分计算和应用的一点注记

陈 军 胜

(宁夏大学 机械工程学院，宁夏 银川 750021)

高等数学中定积分计算和应用的一点注记

陈 军 胜

(宁夏大学 机械工程学院，宁夏 银川 750021)

以高等数学教学过程中两个定积分的计算为例，引导学生利用已知几何体体积对定积分计算过程中的错误进行分析，给出正确解题方法；同时利用定积分的计算结果来分析探究特殊几何体的形体。

定积分；几何体体积；高等数学

下面，通过在高等数学教学过程中的两个习题为例，分析学生在解题过程中出现的错误原因，引导学生利用已知几何体的体积与二重积分的计算结果做比较研究。

教材[1]习题8-3中的一道计算题：

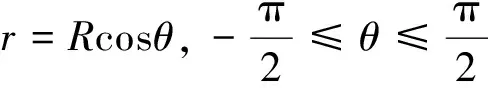
解法2 由于所求的立体关于xoz面对称，于是所截立体的体积V是第一卦限那部分曲顶柱体体积的2倍，即

其中，D2={(x,y)|y≥0,x2+y2≤Rx}，如图3所示。

作极坐标变换x=rcosθ,y=rsinθ，区域D2的边界曲线的极坐标方程为

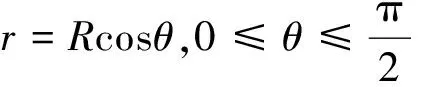
下面这个例题是用积分的计算结果来探究几何体的形体。

教材[2]习题5第5题：

例2 计算底面半径为R的圆，而垂直于底面一固定直径的所有截面都是等边三角形的立体体积。

解 如图4所示，则底面方程为x2+y2=R2。对任意的x∈[-R,R]，过点x且垂直于x轴的截面是一个等边三角形，底和高分别为

于是，立体体积

考察用平行于xoz平面y=y0去截割几何体所得的边界曲线方程，如图5所示。

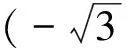
考察用平行于xoy平面z=z0(z0≥0)去截割几何体所得的边界曲线方程，如图6所示。

所以，用平行于xoy平面z=z0(z0≥0)去截割几何体所得的边界曲线方程是两圆的交线。

[1]林伟初. 高等数学(经管类)下册[M]. 2版.上海: 复旦大学社,2013: 73.

[2] 黄立宏. 高等数学上册[M]．3版. 上海:复旦大学社, 2011: 205.

[3] 董艳慧. 对维维安尼(Viviani)体的体积错解小议[J]. 数学教学研究, 2011, 30(10): 62-63.

Note on the Integral Calculation and Application Higher Mathematics

CHEN Jun-sheng

(School of Mechanical Engineering, Ningxia University, Yinchuan 750021, China)

The calculation problem for example encountered two of the definite integral of taking higher mathematics teaching process, we guide students to use the known geometry volume results, why the process error calculation of the definite integral is analyzed, and given the right method for solving. At the same time, we use the definite integral computation result analysis to explore a special geometry shape.

definite integral, geometry, higher mathematics

2015-04-02

陈军胜，男，宁夏西吉人，硕士，宁夏大学机械工程学院副教授，研究方向为随机分析、数学优化。

时间：2016-1-5 13:01 网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160105.1301.030.html

O13

A

1007-4260(2015)04-0120-03

10.13757/j.cnki.cn34-1150/n.2015.04.030