Gronwall不等式的证明及有关应用

彭 良 香

(江苏城乡建设职业学院 基础部，江苏 常州 213147)

Gronwall不等式的证明及有关应用

彭 良 香

(江苏城乡建设职业学院 基础部，江苏 常州 213147)

在证明Gronwall不等式的基础上，应用Gronwall不等式来证明存在唯一性定理中的唯一性、解的不等式、特殊的初值问题的解的存在性，以及有关微分方程及摄动方程的解的渐近性质。

Gronwall不等式；初值问题；摄动方程；渐近性质

Gronwall不等式是常微分方程课程[1-6]中的一个重要不等式，本文给出了两种证明方法及相关应用。

Gronwall不等式[1]设K为非负常数，f(t)和g(t)为在区间α≤t≤β上的非负连续函数，且满足不等式

(1)

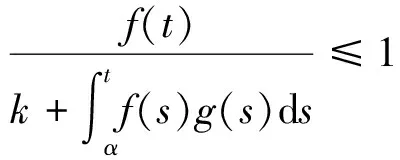
下面利用Gronwall不等式来证明一阶微分方程解的存在唯一性定理中的唯一性。

定理1[1](存在唯一性) 如果f(x,y)在矩形区域R：|x-x0|≤a,|y-y0|≤b上连续且关于y满足利普希兹条件，则方程

(2)

存在唯一解y=φ(x)，定义于区间|x-x0|≤h上，连续且满足初始条件φ(x0)=y0，其中

证明 解的存在性证明可见文献[1]。假定φ(x),ψ(x)为在x0≤x≤x0+h上初值问题

利用Gronwall不等式有

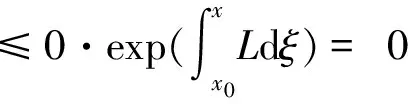
即φ(x)=ψ(x)，唯一性得证。

下面通过几个例子来说明Gronwall不等式在常微分方程中的重要应用。

例1(解的不等式性质) 如果函数f(x,y)于某区间D内连续，且关于y满足利普希兹条件，则对方程(2)的任意两个解φ(x)和ψ(x)，在它们的公共存在的区间内有下面不等式成立，|φ(x)-ψ(x)|≤|φ(x0)-ψ(x0)|·exp(L|x-x0|),

其中x0是所考虑区间内的某一值。

证明 由假设知，在a≤x≤b上，有

当x0≤x≤b时，

|φ(x)-ψ(x)|≤|φ(x0)-ψ(x0)|+

|φ(x0)-ψ(x0)|·exp[L(x-x0)]。

当a≤x≤x0时，类似可证|φ(x)-ψ(x)|≤|φ(x0)-ψ(x0)|·exp[L·(x-x0)]。

故对任意x∈[a,b]都有

|φ(x)-ψ(x)|≤|φ(x0)-ψ(x0)|·exp(L|x-x0|)。

例2 (解的整体存在性) 设函数f(x,y)在区域J×R内连续，J=(a,b)且满足

|f(x,y)|≤p(x)+q(x)·|y|，

其中p(x)、q(x)是J内的连续非负函数，试证：对∀(x0,y0)∈J×R，初值问题

(3)

的解在整个J上存在。

证明 由题知初值问题(3)的解y=φ(x,x0,y0)是局部存在的，设φφ(x,x0,y0)是初值问题(3)在某一区间x0≤x≤β(β∈J)上的解。令M为p(x)在x0≤x≤β上的上界，N为q(x)在x0≤x≤β上的上界，则在x0≤x≤β上有

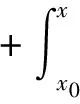
[|y0|+M(β-x0)]·exp[N(x-x0)]≤

[|y0|+M(β-x0)]·exp[N(β-x0)]，

即对∀β∈J,β>x0,φ(x)在[x0,β)上有界。

由解的延拓定理[1]易得：φ(x)向右延拓到[x0,b)上，在α

再考虑微分方程

(4)

摄动方程

(5)

当t→+∞时方程(4)的一切解都趋于零，则方程(4)方阵预解式满足

‖X(t)‖≤α·exp(-σt),t≥0

(6)

例3 (解的渐近性质) 若当t→+∞时方程(4)的一切解都趋于零，又设B(t)是一个连续方阵，满足∫0+∞‖B(s)‖ds<+∞，则当t→+∞时方程(5)的一切解也都趋于零。

证明 令x(t)为方程(5)的任一解，可看成是

x(t)=X(t)x(0)+∫0tX(t-s)B(s)x(s)ds。由(6)式知，‖x(t)‖≤‖X(t)x(0)‖+∫0t‖X(t-s)B(s)x(s)‖ds≤

α‖x(0)‖e-σt+α∫0te-σ(t-s)‖B(s)‖·‖x(s)‖ds，

则exp(σt)‖x(t)‖≤α‖x(0)‖+α∫0t‖B(s)‖·

exp(σs)·‖x(s)‖ds，

由Gronwall不等式得，exp(σt)‖x(t)‖≤α‖x(0)‖·exp(α∫0t‖B(s)‖ds)，

即x(t)→0，t→+∞。

例4[2](解的渐近性质) 设当t→+∞时方程(4)的一切解趋于零，则必存在一数η>0，它只依赖于方阵A，使对足够大的t值，有‖B(t)‖≤η，则当t→+∞时方程(5)的一切解都趋于零。

设‖ξ‖=a，则‖X(t)‖≤aα·exp(-σt)+αη·exp(-σt)∫0texp(σ·s)‖x(s)‖ds，t≥t0,故exp(σt)‖x(t)‖≤aα+αη∫t0texp(σ·s)‖x(s)‖ds≤

由Gronwall不等式知，

从上面的例子看，Gronwall不等式的应用比较广泛，尤其是在证明一些不等式和初值问题的解的性质时。

[1]王高雄, 周之铭, 朱思铭, 等. 常微分方程[M]. 北京: 高等教育出版社, 1997.

[2] 罗梭. 常微分方程[M]. 上海: 上海科学技术出版社, 1981.

[3] 丁同仁. 常微分方程教程[M]. 北京: 高等教育出版社, 2005.

[4] 周尚仁. 常微分方程习题集[M]. 北京: 高等教育出版社, 1984.

[5] 叶彦谦. 常微分方程讲义[M]. 北京: 人民教育出版社, 1983.

[6]B. Braun. Differential Equations and Their Applications[M]. New York: Springer-Verlag, 1993.

Proofs and Applications of Gronwall Inequality

PENG Liang-xiang

(Jiangsu Urban Rural Construction College, Changzhou 213147, China)

First, this paper provides two proofs of Gronwall inequality.Then, we apply it to prove the uniqueness of the existence and uniqueness theorem, the inequality of the solution and the existence of the solution to special initial value problem.At last, we apply it to prove the theorem about the asympototic property of the solution to the differential and perturbed equation.

Gronwall inequality, initial value problem, perturbed equation, asympototic property

2015-04-03

彭良香，女，安徽霍山人，硕士，江苏城乡建设职业学院基础部讲师，研究方向为图论与网络优化。

时间：2016-1-5 13:01 网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160105.1301.029.html

O178

A

1007-4260(2015)04-0117-03

10.13757/j.cnki.cn34-1150/n.2015.04.029