面向高维数据PCA-ReliefF的EP模式分类算法

程玉胜，胡 飞，程百球

(安庆师范学院 计算机与信息学院，安徽 安庆 246133)

面向高维数据PCA-ReliefF的EP模式分类算法

程玉胜，胡 飞，程百球

(安庆师范学院 计算机与信息学院，安徽 安庆 246133)

针对高维数据集，文中提出一种PREP(PCA-ReliefF for EP)算法：首先采用PCA和ReliefF算法实现特征降维；然后利用EP模式思想，构造精度更高、规模更小的EP模式分类器；最后利用标准数据集对文中的方法进行测试。实验结果表明，在对高维数据进行分类时，该方法构造的分类器在预测精度和运行时间上均有较大幅度的提升。

分类器；特征选择；PCA-ReliefF；EP模式；PREP算法

分类在科研、医学等诸多领域都具有广泛的应用。目前广泛使用于统计学习[1-2]和数据挖掘等领域的常用分类方法大多是基于决策树、距离或者神经网络等。随着大数据时代的到来，传统分类方法已然不再适用。Dong等人创造性的提出一种新兴的EP模式分类算法，即初始时从项集出发采用类似关联规则的数据挖掘算法来挖掘EP模式。经过实验证明，EP模式分类器在分类精度和时间性能上相比于其他分类器有很大的优势。但是同样在面对高维数据时，其中的冗余数据造成了彼此之间很强的相关性，在挖掘过程中，不可避免的形成了对分类器产生负面影响的冗余模式。因此，Li等人又提出了一种改进后的JEP-Classifier算法[3]，该算法具有很好的区分能力，能过滤不必要的EP模式，但是JEP分类器适用范围较小，即覆盖率偏低。于是Fan等人[4]提出了一种基本的显露模式-eEp，能够在确定并保留核属性的同时，去除无关的分类模式。F.Berzal等人[5]提出了增加最小增长率差这一约束条件的ConsEPminer算法。S.Haykin[6]提出的基于边界EP模式算法，通过操作左右边界的变化来得到理想的EP模式，在挖掘过程中有效的避免了复杂数据带来的冗余EP模式。H.Fan等人[7]后来提出的SJEP算法，在JEP模式的基础上加入JEP模式必须满足支持度阈值的约束条件；许洪涛[8]在对中文文本分类时，先使用特征选择进行有区分能力的核心属性的提取，最后提出基于eEPs的中文文本分类方法TCEP，该方法在一定程度上缓解了维数灾难，也比较适合一般的大规模文本分类。施万锋等人[9-10]提出一种基于lasso的EP模式分类算法，在特征选择时采用惩罚函数去除无用特征，有效保留重要的EP模式，但在此模式下，对超高维数据和高维小样本数据没有良好的分类效果，还存在较多的拟合现象。

针对数据维数较高、形式较为复杂的情况下，上述的方法没有较好的性能。因此，本文基于EP模式分类器思想，提出了一种新的方法PREP：首先利用主成分分析[11-12](PrincipleComponentAnalysis，PCA)约简存在相关性的特征，然后利用ReliefF算法[13-15]对权值较重的属性进行特征提取[16]，最后使用基于显露模式(EmergingPattern，EP) 的分类器对预处理后的数据集进行分类。该方法在保留重要属性信息特征的同时，也能快速高效的进行分类。

1 EP模式分类

1.1EP模式基本概念

EP模式的分类方法从关联规则中得到启发，从项集支持度和增长率的角度去决定如何分类，即当两个数据集中某个项集明显出现支持度的变化时，那么该项集可以当做区分不同数据集的一个核心属性，该项集便具备良好的分类性能。

用{A1，A2，…,An}表示属性集，Aj表示特征，{a1，a2，…,an}表示实例，a1，a2，…,an分别对应于A1，A2，…,An特征的值，将其中的(Aj=aj)为一个项。若从逻辑上来定义，数据集D中所有项的集合为M,如果X中的项均存在于Y中，但Y中的项不一定都在X中找到时，便可以称项集X包含于Y。

定义2 假设D′和D″分别表示两个不同类别的数据集，用si(x)表示项集X在数据集Di中的支持度。项集X从D′到D″的增长率为

定义3 假设增长率阈值ρ>1,如果grD′→D″(X)≥ρ，那么就称项集X是从D′到D″的EP模式，简称为D″的EP模式。

EP模式增长率的大小作为分类能力强弱的标准，他们之间存在着正比的关系，而支持度与该EP模式的分类范围的关系也是如此。如表1所示。

表1 EP模式的事例

其中ρ=3。在被当做优秀范例的蘑菇集试验中，做出如下解释：数据集由有毒蘑菇类和无毒蘑菇类组成，其中含有很多有效或者无效的EP模式。表中的数据对应的支持度和增长率如下，

e1={(ODOR=none)，(GILL_SIZE=

broad)(RING_NUMBER=one)}，

e1在有毒类中的支持度为0，在可食用类中的支持度为63.9%，在这里可食用类和有毒类分别为目标类和非目标类。根据定义，e1增长率为∞，也就是可食用蘑菇类的一种EP模式。所以，根据e1挑选的蘑菇一般是可食用蘑菇。

e2={(BRUISES=no),(GILL_SPACING=

close),(VEIL_COLOR=white)}，

e2是一个有毒蘑菇类的EP模式。在可食用和有毒类蘑菇中包含有e2实例的比例分别为3.8%和 81.4%，其增长率为21.4。因而，具有e2特征的蘑菇在很大程度上是有毒的。

1.2 EP模式分类器构造过程

对于一个给定的g维数据集D，设定合适的支持度sup和增长率ρ。在这里要说明一点，面对高维数据的时候，要提高算法的性能和减少运行的时间，那么对应的支持度要设置的比较高，而增长率可以根据实际的情况来自行调节。首先，开始扫描每一个属性(单项集)，分别计算它们的支持度以及在各类之间的增长率，如果某个一项集(即单个属性)对应的支持度和增长率均大于给定的sup和ρ，那么将所有满足该条件的一项集放入一个集合中。然后，再扫描由一项集中两两构成的二项集，同理，当某个二项集对应的支持度和增长率也都大于sup和ρ时，将它们放入二项集集合中。接下来的步骤同上述一样，项集数目不断增加(最大数为g)，直到找不到满足条件的项集为止。最后就是如果确定EP模式了，对于取得的各项集的集合，按照ρ和sup的大小从大到小进行排序，输出排在第一位的项集，即构成最后的EP模式。

EP模式分类器构造过程如图1所示。

图1EP模式分类器分类过程

2 结合PCA和ReliefF的EP模式分类算法(PREP算法)

对于高维数据的分类，首先要进行降维处理，利用主成分分析去除冗余的属性特征，保留核心属性的同时完成高维空间到低维的映射，然后根据ReliefF算法思想对保留下来的属性赋予体现重要程度的权值，权值的大小代表着该特征对于分类准确的贡献度，最后选择特征权值最高的前d个特征构成最后的核心特征子集。

在目标类为两类的情况下，如果训练样本集为D={(x1,y1),(x2,y2)，…，(xn,yn)}，其中xi∈Rn，yi是xi类标签yi∈{-1，1}，则基于PCA-ReliefF的EP模式分类算法详细描述如下所示。

PREP算法的主要步骤：

输入：高维训练集D，迭代次数t，k个最近邻样本，目标维数d，有效核心特征集合s，s>d。

步骤1 对随机产生的训练数据集D0进行主成分提取，将权值较大的前s个主成分存入数据集D1；

步骤2 首次将D1各特征权值归零；

步骤3 随机确定D1中的一个样本X；

步骤4 分别任意选取与X同类和异类的k个近邻，分别记为Pj和Mj(c)，其中j=1,2,…,k，c≠c(X)，c=1,2,…,C,C为样本类别数，c(X)表示样本所属的类别；

步骤5 在此更新各个特征权值W(a)，权值更新公式为，

(1)

步骤6 重复执行筛选过程t次，输出每个特征的权值W(i)；

步骤7 按顺序保留权值最大的前d个特征构成特征集；

步骤8 采用EP模式分类。其主要步骤：

给定训练数据集D′(假定以最简单的两类问题)，给定支持度、增长率阈值。

(1)挖掘D1与D2之间相互的EP模式集E1和E2；

(2)约简E1,E2中的EP模式；

(3)通过相应的公式分别计算两个类的基础分；

(4)对于实例t，计算它在每个类中的规范化值norm＿score(t,Ck),将实例归为分值最大的类。

其中，将特征a为标准量时，样本X、Y之间的距离为d(a,X,Y)；p(c)表示第c类目标的概率，也就是用该类目标在数据集中的样本总数除以总样本总数，当各类目标样本数大致相同时，p(c)=1/C；Mj(c)表示第c类目标的第j个样本；m和k的取值由样本的总数量和维度数量综合决定。待分类样本t对每个类的规范化分norm＿score(S,C),可以按照如下公式得到：

agg＿score(S,C)=

(2)

(3)

PREP分类算法流程如图2所示。

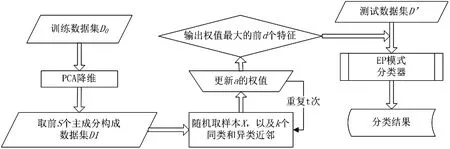
图2 PREP分类算法流程

3 实验结果及析

3.1 实验结果

测试运行环境为Windows XP操作系统，3.29 GHz的i3-2120 CPU，1.98 GB的内存，编程使用JAVA语言，工具为MyEclipse。为了验证PREP分类算法所具有的时间优越性和精度，本文所选取的数据集都是取自UCI数据库，数据类别数都是两类。如表2所示，ionsphere，madelon和lungcancer具有的样本数分别为351，2 000和181，而属性总数分别为34，500和12 534。在实验中，首先将PREP算法和CAEP算法进行比较，比较的内容有时间和精度，实验结果如表3所示。然后改变迭代的次数(k分别取值10和5，m的值取10)。为使实验结果有较高的可信度，实验的训练集和测试集都是随机生成(各占总数的50%)，设置PREP和CAEP的增长率为20，最小支持度为0.005和0.01。

表2 实验使用的数据集描述

表3 CAEP和PREP实验对比

为了直观的观察目标维数和阈值变化对实验结果的影响，实验中，对选取的3个测试数据集进行了相应结果绘制，如图3～图5所示。

3.2 实验结果分析

由表2选择的数据集可以知道，为了体现算法的优越性，使用了特征维数较高的3个数据集，由于目前大多数数据集为两类，并且对于多类问题可以转化为两类问题解决，因此实验中选择为两类。对于Ionsphere数据集，CAEP算法和PREP 算法在正确率上相差不是很多，但是在运行时间上，PREP算法时间减少了近9/10，相差很大。从Madelon，Lungcancer两个数据集的实验情况看，CAEP算法已经因为内存溢出或者产生的规则太多而不能进行分类了，但是PREP算法在进行了特征降维后，能够正常的分类，在分类的正确率和时间消耗上也有不错的表现。由图3，4，5可以看出，算法在准确率和时间消耗上在一定范围内均表现出一定的波动性。说明实验结果都是在k=10的情况下取得的。对k=15或者k=5也进行了测试，发现k=10时，能取得令人满意的结果。

表3的实验数据是在综合考虑时间消耗和正确率的情况下取值的。总的来说，在阈值和目标维数合适的情况下，经过PCA-ReliefF的EP模式分类算法，在保证有效信息保留和减少运行时间的同时，也能够保证分类的准确率。

4 结束语

针对维数较高的数据集，本文提出了一种基于PCA和ReliefF的特征选择方法，首先去除相关性较强的特征互相间产生的干扰，然后进行特征选择，最后使用EP模式分类算法进行分类。实验结果表明，该算法能够在保留住核心信息的同时，去除了冗余和互相之间相关性较强的特征，有效减少了运行时间，并且在分类精度上取得了不错的结果，具有较好的性能。但是，对于小样本数据或者数据维数很大的时候，算法的时间效率显得不高或者计算量偏大，算法还存在执行不下去的问题；另外k值选取问题，还没能建立一个有效简洁的标准，只能通过多次实验的对比而确定，不免会因为重复操作而带来过多的时间消耗。这些都是下一步需研究的问题。

[1]S.Gnanapriya,R.Suganya,G.S.Devi,etal..Datamining:conceptsandtechniques[J].DataMining&KnowledgeEngineering, 2010, 26(1): 32-38.

[2]马红娟, 赵秀兰, 孙亚萍, 等. 基于数据挖掘技术的概率统计教学研究[J]. 经济研究导刊, 2015(6): 220-222.

[3]JinyanLi,GuozhuDong,K.Ramamohanarao.Makinguseofthemostexpressivejumpingemergingpatternsforclassification[J].KnowledgeandInformationSystems, 2001, 3(2): 1-29.

[4]JinyanLi,GuozhuDong,K.Ramamohanarao.DeEPs:anewinstance-basedlazydiscoveryandclassificationsystem[J].MachineLearning, 2004, 54(2): 99-124.

[5]F.Berzal,J.C.Cubero,S.J.Maria.Ahybridclassificationmodel[J].MachineLearning, 2004, 54(1): 67-92.

[6]S.Haykin.Neuralnetworks:acomprehensivefoundation[J].ComputationSystems, 1999, 4(2): 188- 190.

[7]H.Fan,K.Ramamohanara.Fastdiscoveryandthegeneralizationofstrongjumpingemergingpatternsforbuildingcompactandaccurateclassifiers[J].IEEETransactiononKnowledgeandDataEngineering, 2006, 18(6): 721-737.

[8]许洪涛. 一种基于eEPS的中文文本自动分类算法[D]. 郑州: 郑州大学, 2006.

[9]施万锋, 胡学钢, 俞奎. 一种面向高维数据的迭代式lasso方法[J]. 计算机应用研究, 2011, 28(7): 4463-4466.

[10]施万锋, 胡学钢, 俞奎. 一种面向高维数据的均分式lasso方法[J]. 计算机工程与应用, 2012, 48(1): 157-161.

[11]余映, 王斌, 张立明. 一种面向数据学习的快速PCA算法[J]. 模式识别与人工智能, 2009, 22(4): 567-573.

[12]唐懿芳, 钟达夫. 主成分分析方法对数据进行预处理[J]. 广西师范大学学报, 2002, 3(1): 223-225.

[13]张丽新, 王家廞, 赵雁南, 等. 基于Relief的组合式特征选择[J]. 复旦学报(自然科学版), 2004, 43(5): 893-898.

[14]吴浩苗, 尹中航, 孙富春.Relief算法在笔记识别的应用[J]. 计算机应用, 2006, 26(1): 174-177.

[15]蒋玉娇, 王晓丹, 王文军, 等. 一种基于PCA和ReliefF的特征选择方法[J]. 计算机工程与应用, 2010, 46(26): 170-172.

[16]陆景辉. 基于信息理论的特征选择算法研究[D]. 北京: 北京交通大学, 2007.

EP Pattern Classification Algorithm for High Dimensional Data Based on PCA-ReliefF Computer Engineering and Applications

CHENG Yu-sheng, HU Fei, CHENG Bai-qiu

(School of Computer and Information, Anqing Teachers College, Anqing 246133, China)

For high dimensional data sets, PREP (PCA-ReliefF for EP) algorithm is presented. Firstly, the feature dimension reduction is realized by using the PCA and ReliefF algorithm. Then, higher precision and smaller EP classifier is constructed by using the EP model of ideological construction. Finally, the method of PREP is tested by using the standard data. The results show that structured classifier constructed by this method has a great improvement in the prediction accuracy and running time for the high dimensional data.

classification model, feature selection, PCA-ReliefF, EP model, PREP algorithm

2015-04-07

程玉胜，男，安徽桐城人，博士，安庆师范学院计算机与信息学院教授，硕士生导师，主要从事文本挖掘、粗糙集理论等方向的研究；胡飞，男，安徽安庆人，安庆师范学院计算机与信息学院硕士研究生，主要研究领域为机器学习、数据挖掘等。

时间：2016-1-5 13:01 网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160105.1301.008.html

TP182

A

1007-4260(2015)04-0028-05

10.13757/j.cnki.cn34-1150/n.2015.04.008

项目名称： 安徽省高等学校自然科学基金(KJ2013A177)。