柯西不等式的一个注记

张华民，梅 红

(蚌埠学院 数学与物理系，安徽 蚌埠 233030)

柯西不等式的一个注记

张华民，梅 红

(蚌埠学院 数学与物理系，安徽 蚌埠 233030)

利用向量的勾股定理证明了线性代数中的柯西不等式和三角不等式，探讨了这两个不等式的联系，并用三角不等式证明了柯西不等式，指出了该不等式名称中一个易被忽视的细节。

勾股定理；柯西不等式；三角不等式

线性代数是理工科大学生的一门重要课程，学好这门课对理工科大学生后继课程的学习具有重要意义。如何上好这门课，人们已做了许多工作[1-3]，笔者也进行了有益的尝试[4-5]。本文主要探讨了向量的勾股定理，并用它证明柯西不等式和三角不等式，建立这两个不等式间的联系，并指出柯西不等式名称中一个易忽略的细节。

1 向量内积的几何意义

内积是线性代数中的一个重要概念，欧氏空间中的许多概念和方法都与内积相关。下面给出内积的定义与几何意义。由于诸多文献中对内积的记号表示不尽相同[6-10]，例如文献[6]是用圆括号(小括号)，文献[7]是用方括号(中括号)，文献[8-9]是用尖括号，文献[10]是用实心点表示的。本文记号以文献[6]为准。先给出内积的定义。

定义1 设V是实数域R上的一个线性空间，在V上定义了一个二元实函数，称为内积，记作(α,β)，它具有以下的性质：

(1)(α,β)=(β,α);

(2)(kα,β)=k(α,β);

(3)(α+β,γ)=(α,γ)+(β,γ);

(4)(α,α)≥0,当且仅当α=0时, (α,α)=0。

其中α,β,γ∈V,k∈R。规定当且仅当两向量的内积为零时，称两向量是正交的。

定义内积的二元实函数有很多种，通常的定义有下面两种，一是在向量空间Rn中，取α=(a1,a2,…,an)T,β=(b1,b2,…,bn)T, 则向量α和β的内积(有的文献也称为点积、数量积[10])定义为(α,β)=a1b1+a2b2+…+anbn，若引入求和符号∑、向量和矩阵来表示，记n阶单位矩阵为I, 则上式又可写为

βTα=αTIβ=βTIα。

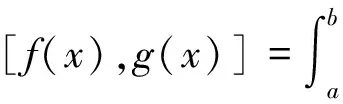
‖α‖≥0,‖kα‖=|k|‖α‖ 。

若 ‖α‖=1则称其为单位向量，记为αe。

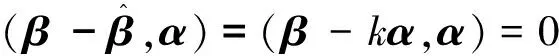
由内积的性质，化简得到

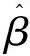
(1)

即向量β与α内积的几何意义。更进一步，若取α为单位向量，即有‖α‖=1=(α,α)，此时记

α=αe，则上式可写为

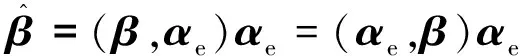
即向量β与单位向量αe的内积(β,αe) 为向量β在单位向量αe的方向上正投影的数量积[10]。

2 两个重要不等式的证明

柯西不等式

|(α,β)|≤‖α‖ ‖β‖

(2)

和三角不等式

‖α+β‖≤‖α‖+ ‖β‖

(3)

是两个著名的不等式。一般线性代数或高等代数教材通常是利用向量α,β的线性组合α+tβ来构造内积，由内积(α+tβ,α+tβ)的非负性，证得不等式(2)；利用内积的定义将恒等式‖α+β‖2=(α+β,α+β) 展开，然后利用不等式(2)证得三角不等式(3)。这样证明过程简洁明了，但容易给人造成误解，感觉是柯西不等式强于三角不等式。实际上这两个不等式间虽有上述的联系，但彼此互相独立，它们都可直接由向量的勾股定理得到。下面直接用向量勾股定理来证明这两个著名的不等式。

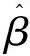
(4)

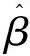
证明 由(1)式有

(5)

化简得

进一步化简得|(α,β)|≤‖α‖‖β‖

这样就证明了著名的柯西不等式。

注1 不等式(2)是历史上有名的不等式，该不等式的离散形式为[11]

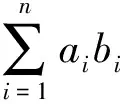
注2 在不同的文献上不等式(2)的名称也不尽相同。例如在文献[6]中称为柯西-布涅柯夫斯基不等式，在文献[7]中称为施瓦兹不等式，在文献[2,13]中称为施瓦茨不等式。这里需要对施瓦兹或施瓦茨说明一下， Laurent Moise Schwartz (1915.03.05-2002.07.04) 是法国人, 因在分布理论、泛函分析、概率论方面的卓越贡献获得1950年的菲尔兹奖[13]，另一位是Hermann Amandus Schwarz (1843.01.25-1921.11.30)，他是德国数学家，魏尔斯特拉斯的学生，研究并发现了施瓦兹极小曲面，柯西-施瓦兹不等式就是以他的名字命名的[14](除引用别的文献中名称外，本文均将Schwarz译为施瓦兹)。把这两个人弄混淆并非只发生在汉语文献里，在Gene H. Golub和 Charles F. Van Loan[15]经典著作的正文和索引里都把这个不等式称为Cauchy-Schwartz-inequality[15]，而在对应的中国科学院袁亚湘翻译的汉译本矩阵计算[16]的正文中仍称为Cauchy-Schwartz不等式，而在索引中则称为Cauchy-Schwarz不等式。

下面用(1)式来证明三角不等式。

证明 记γ=α+β, 则有

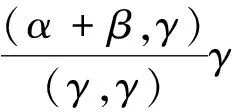
‖α‖+‖β‖。

若(α,γ)与(β,γ)同号，则第一个不等号中等号成立，若(α,γ)与(β,γ)异号则小于号成立，第二个不等号用到了(5)式中的结论。

一般文献中多用柯西不等式来证明三角不等式，下面反过来用三角不等式来证明柯西不等式。

证明 由三角不等式‖α+β‖≤‖α‖+‖β‖两边平方，并进一步化简有

(‖α+β‖)2≤(‖α‖+‖β‖)2，(α+β,α+β)≤(α,α)+2‖α‖‖β‖+(β,β)，

(α,β)≤‖α‖‖β‖

(6)

在上面的证明过程中β用-β代替，化简得到

-(α,β)≤‖α‖‖β‖

(7)

将(6)、(7)两式结合，即证得(2)式成立。

由上面的证明可看出柯西不等式与三角不等式是源于勾股定理的两个相互独立的不等式。

3 结束语

根据向量的勾股定量，证明了著名的柯西不等式和三角不等式，讨论了这两个著名不等式间的联系，用三角不等式证明了柯西不等式，理清了柯西不等式命名中一个易被忽视的细节。

[1] 李尚志. 从问题出发引入线性代数概念[J]. 高等数学研究, 2006, 9(5): 6-9.

[2] 陈建龙, 张小向. 深化教学方法改革培养学生创新能力[J]. 大学数学, 2010, 26(1): 34-36.

[3]D. C. Lay. Linear Algebra and Its Applications [M]. 3rd. Boston: Addison Wesley, 2005: 379.

[4] 张华民, 殷红彩. 范德蒙行列式的几种证法[J]. 蚌埠学院学报, 2013, 2(3): 15-18.

[5] 张华民, 殷红彩. 高等代数教学中的几点思考[J]. 安庆师范学院学报(自然科学版), 2014， 20(1)：90-93.

[6] 王萼芳, 石生明. 高等代数[M]. 3版. 北京：高等教育出版社，2007: 359-360.

[7] 同济大学数学系. 线性代数[M]. 5版. 北京：高等教育出版社，2007: 111-112.

[8] S. K. Jain, A. D. Gunawardena. Linear Slgebra: An Interactive Approach [M]. Beijing: China Machine Press, 2004: 188-189.

[9] 张贤达. 矩阵分析与应用[M]. 北京：清华大学出版社，2004: 18-19.

[10] 吕林根, 许子道. 解析几何[M]. 4版. 北京：高等教育出版社，2006: 37-38.

[11] G. H. Hardy, J. E. Littlewood, G. Pòlya. Inequalities[M]. Beijing: Posts & Telecom Press, 2008: 12.

[12] 王卿文. 线性代数核心思想及应用[M]. 北京: 科学出版社, 2012: 403.

[13] 李文林. 数学史概论[M]. 3版. 北京: 高等教育出版社, 2011: 285.

[14]A. G. Catherine. The Facts on File Geometry Handbook [M]. Beijing: Guangming Daily Press, 2004: 218.

[15] G. H. Golub, C. F.V.Loan. Matrix Computations [M]. 3rd. Beijing: Posts & Telecom Press, 1996: 153.

[16] G. H. Golub, C. F.V.Loan. 矩阵计算[M]. 袁亚湘, 译. 北京: 科学出版社, 2001: 59.

Note of the Cauchy Inequality

ZHANG Hua-min，MEI Hong

( Department of Mathematics and Physics, Bengbu University, Bengbu 233030, China)

By using the Pythagorean theorem of vectors, the Cauchy inequality and the triangle inequality are proved and the relationship of these two inequalities are discussed. The Cauchy inequality is proved by using the triangle inequality. Moreover, an ignored detail in the name of the Cauchy inequality is pointed out.

pythagorean theorem, Cauchy inequality, triangle inequality

2015-04-27

2013省级质量工程项目(2012GXK106)，2013教学团队(jxtd02)，省级质量工程(2014zy141)和院级项目 (2015ZR10)。

张华民，男，安徽蚌埠人，博士，蚌埠学院数理系副教授，主要从事线性代数的教学和研究。

时间：2016-1-5 13:01 网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160105.1301.031.html

O151.2

A

1007-4260(2015)04-0123-03

10.13757/j.cnki.cn34-1150/n.2015.04.031