基于排序树的Node-Apriori改进算法

毕玉萍，胡世昌，李劲华

(青岛大学数据科学与软件工程学院，青岛266071)

随着互联网的运用和普及，信息的产生和传播日益迅速与便捷，数据信息在爆炸式地增长。信息存储单位从之前以G 为单位，到现在以PB甚至EB为单位。网上浏览的信息，各种社交App中发表的语言动态，各种购物平台购买的商品以及其他网上行为，都会被视为数据信息加以记录和储存。互联网数据信息的增长，让许多行业看到了机遇，在这些数据信息中筛选有效的用户信息，给予精准的推荐与利用，是可以产生巨大的商业利益的[1]。但随着数据的不断增加和累积，无效信息也会越来越多，信息过量的问题也随之产生，这对许多行业提出了挑战。面对海量的数据信息，如何在海量含有噪声的信息中筛选出隐藏的有效信息成为一个急需攻克的难题[2]。从大量信息中挖掘有效信息的技术越来越重要，数据挖掘技术和算法应运而生[3]。数据挖掘是指从大数据中通过算法提取隐藏信息的过程，在1989年的人工智能专题研讨会上首次提出[4]。关联规则挖掘是其中的一个重要研究方向，有着广泛的应用。例如分析之前招生的学生成绩以及地域从而找到合适的关联规则进行更为有效的招生[5]，或者根据调查问卷挖掘有效的关联规则为奥赛选拔学生提供了有效信息[6]，利用药房和药店等医疗保健系统产生大量的交易数据挖掘药房处方药物规则[7]，挖掘事物营养成分之间的关联规则从而提高人类营养的吸收[8]，利用关联规则分析海事事故[9]等。针对关联分析领域传统的Apriori算法效率低的问题，文献[10]提出了BE-Apriori(Binay Encoded Apriori)算法，其利用二进制数在内存及运算速度上的优势，对事务记录进行二进制编码后加载到内存，然后利用等效的二进制数之间运算代替集合之间的运算，改进了Apriori算法的效率。文献[11]提出了Tree-Apriori(Tree based Apriori)算法，指出Apriori算法同级节点中每个节点包含的事务记录是可能重复的，利用FP-Tree(Frequent Pattern-growth)的方式组织事务记录，每个节点都代表一棵子树，通过对树中节点进行合并和更新的操作完成频繁项集的挖掘。本文在文献[10]和文献[11]的基础上进行了改进，通过二进制编码的方式，提出了一种改进的Node-Apriori算法。

1 Apriori算法

1.1 基本概念

Apriori算法[12]有两种方式统计候选项集的支持度:对于每个候选项集遍历事务记录统计；对于每个事务记录统计对该事务记录包含的候选项集的支持事务数加1[13]。假如匹配到trie树中的某个节点，该节点有n 个孩子节点，还需要匹配的事务记录为t′，下一步需要做的就是如何在这n 个孩子节点中找到和t′匹配的项。通常有三种方式[14]:

1)孩子节点和事务记录同时遍历。利用两个指针，第一个指针指向事务记录t′的第一项，第二个指针指向第一个孩子节点。比较两者按照频繁1-项集频次中的顺序，小者进行移动，如果指向事务记录的第x项则指针指向第(x＋1)项，如果指向第k 个孩子节点，则指针指向第(k＋1)个孩子节点。如果两者相同，则同时移动。这些操作的时间复杂度为O(n ＋|t′|)；

2)二分搜索。有两种基本的方式，或者两者的结合。对于事务记录t＇，找到对应的孩子节点，由于事务记录中的项是排序过的，所以可以使用二分搜索搜索在孩子节点中搜索t′中第一项所在的孩子节点；或者对于的孩子节点，使用二分法搜索该孩子节点在t′的位置。两者的时间复杂度分别为O(|t′|log n)和O(n log|t′|)，可以两者相结合的使用，选择其中较小的一个作为二分搜索的维度；

3)使用数组的方式。数组的长度为频繁1-项集的个数，每个位置代表频繁1项集中的一个项，如果存在则为1，不存在则为0。可以确定每个孩子节点在数组中对应的项，如果该项存在，则可以进行下一步的搜索。利用孩子节点在频繁1-项集按频次排序后的索引，可以立刻计算出在事务记录的中位置。时间复杂度为O(n)。

1.2 算法描述

Apriori算法中挖掘频繁项集的步骤如下:扫描数据库，获取所有项的支持度，获取频繁1-项集。

1)连接:若两个频繁k-项集A 和B 其中有(k-1)项相同，则这两个频繁k-项集可以连接产生候选(k＋1)-项集；

2)剪枝:根据Apriori算法的性质非频繁项集的超集也是非频繁项集，可以对产生的候选项集进行剪枝[15]。若对一个项集的所有子集都进行是否是频繁项集的判断，由于一个k-项集的所有子集数量为2k，则这个过程的时间复杂度为O(2k)，显然是不符合实际的。由于一个频繁项集的子集都是频繁项集，所以假如一个候选(k＋1)-项集的k 个k-项子集，都是频繁项集，那么此候选(k＋1)-项集的非空子集就都是频繁项集，即该(k＋1)-项集就不会是非频繁项集的超集，通过性质1剪枝，复杂度由O(2k)减少到了O(k)。剪枝的依据可以是若(k＋1)个候选频繁(k＋1)-项集的每个k-项子集是否都是频繁k-项集来判断，即有一个或者多个k-项子集不是频繁k-项集，那么该候选(k＋1)-项集不可能为频繁(k＋1)-项集[16]。通过这种方式可以有效剔除一定不是频繁项集的候选项集；

3)通过遍历数据库，对候选频繁(k＋1)-项集的支持度进行统计，若低于最小支持度，则滤除；

4)循环执行2)～4)步，直到不能通过连接产生候选频繁项集为止。

1.3 Apriori算法的缺陷

Apriori算法的缺点主要如下[17](通过频繁k-项集产生频繁(k＋1)-项集来举例):

1)连接的步骤计算效率低下。要判断任意两个频繁k-项集是否有(k-1)项相同；

2)每个候选(k＋1)-项集是否是频繁k-项集还需要遍历(k＋1)次数据库，但是I/O 存取的消耗相对于内存存取要高几个数量级[18]；

3)在扫描数据库时需要对候选项集和事务进行模式匹配，这个过程需要消耗大量的时间[19]。

1.4 FIMIST算法

FIMST 算法[20]采用了前缀树的方式组织项集，兄弟节点具有相同的前缀，这样FIMST 算法在连接的过程中只需要连接兄弟节点即可。并且采用了末项剪枝的概念，若两个兄弟节点不是频繁项集，那么两个兄弟节点连接成的候选项集必定不是频繁项集，来进行剪枝。然后遍历事务记录，统计同一级候选项集节点的支持事务数，对于一条事务记录，如果不包含前缀树的一个节点，那么这个事务记录必定不包含此节点树中所有节点代表的候选项集，以此来提高通知候选项集支持度的效率。利用频繁k-项集对事务记录做了一次筛选，避免了每条事务记录都需要扫描所有候选项集来统计支持度。该算法在连接、剪枝以及统计候选项集支持度的过程中都提高了算法的执行效率。

2 Node-Apriori算法

2.1 基本概念

节点按照一个规则排序后，候选项集的产生是有迹可循的。例如统计所有的事务记录之后频繁-1 项集排序结果为a、b、c、d，那么排序后的所有事务记录不可能包含顺序为c、b 子序列的事务记录，而排序后的事务记录中不可能包含子序列c、b。如果一个事务记录包含的I为{a，b，c，d}，那么可能产生的候选项集如图1表示。

首先按照规则排序的频繁1-项集，然后对于每个节点只能与节点在排序中的位置之后的元素才可能生成候选项集，这些节点组成的树称为排序树，树中节点的深度代表的时候频繁项集或者候选项集的长度，每个节点都代表一个频繁项集或者候选项集。

这样不需要像Apriori算法那样进行连接产生候选项集。Apriori算法连接的时间复杂度为O(n2)，n 为频繁k-项集的个数。而通过这种方式组织节点之后，由于每个节点子节点的前缀都是相同的，所以连接的过程仅需要对有大于1个孩子节点的节点进行连接，其时间复杂度为O(k2)，k 为该节点含有子节点的个数。与原方法相比，并不需要对每两个频繁－k 项集的前(k－1)项相同进行判断，仅需要对子节点之间顺序连接即可，大大提高了算法连接过程的效率。

事务记录的存储是可以嵌入到节点中。每个频繁项集节点包含的事务记录都是包含此项集的事务记录。在统计候选项集支持度的时候，无需遍历所有事务记录，对于频繁项集包含的事务记录可以采用方式2对该节点的子节点统计支持度。因为父节点表示项集的是子节点表示的项集的子集，而包含子节点的事务记录，必定包含父节点表示的项集，父节点的事务记录是全部事务记录的子集，减少了统计候选项集需要遍历的事务记录的数量。由于Apriori算法中统计候选项集支持度是最消耗时间的步骤[21]，所以增加的属性事务记录可以极大的提高算法挖掘频繁项集的效率。

由于事务记录繁多时，不可能全部加载进入内存，即不可能直接给每个节点添加未加处理的事务记录。通过二进制编码的方式可以有效的减少事务记录内存的占用[21]，使用二进制之间的运算还可以替换集合之间的运算。这样就可以有效解决事务记录占用内存较大的问题，并有效的提高算法的执行效率。

二进制编码:若频繁1-项集的个数为n，则可以把所有项集编码为长度小于或等于n 位的二进制数。长度为n 的二进制数中的每个位置分别代表每个项。若某项在此项集中存在，则在该位置为1；若该项在此项集中不存在，则该位置为0。编码后的二进制数可能小于n，这是由于二进制数前面部分位置代表的项均不存在。据此可以对所有事务，频繁项集和候选项集进行编码。然后，通过长度小于或等于n 的二进制数代表频繁项集和候选项集以及事务记录。

性质1编码后的项集a 和项集b。a&b 的结果为项集a 和项集b 共同含有的项集；例如若频繁1-项集为{A，B，C}，项集a－{A，B}二进制编码的结果为110，项集b－{A，B，C}二进制编码的结果为111，项集c－{A，C}二进制编码的结果为101。a&b＝a，表明{A，B}为{A，B，C}的子集，a&c! ＝a，表明{A，B}并非{A，C}的子集。

性质2对于排序树中第k 层的结点A 和B，结点A 表示的频繁项集为{A[1]，A[2]，…，A[k]}，结点B 表示的频繁项集为{B[1]，B[2]，…，B[k]}，若结点B 是结点A 兄弟节点，则有A[1]＝B[1]，A[2]＝B[2]，…，A[k－1]＝B[k－1]，A[k]! ＝B[k][14]。

性质3对于排序树中第k 层节点A 和其子节点B，那么B 代表的项集是A 代表的项集的超集，即，A属于⊆B只有在事务记录包含A 代表的项集的情况下，才可能包含B 代表的项集。

2.2 实例介绍

现举例说明本文算法，事务记录如表1所示，设定挖掘频繁项集的最小支持度为0.4。候选1-项集的支持事务数如表2所示。去掉支持度小于0.4的候选1-项集“4”之后，按照支持度从大到小排序的频繁1-项集的结果为:“3”，“2”，“1”，“5”。编码后的频繁1-项集如表3所示。对每个事务记录进行二进制编码，编码后的事务记录如表4所示。

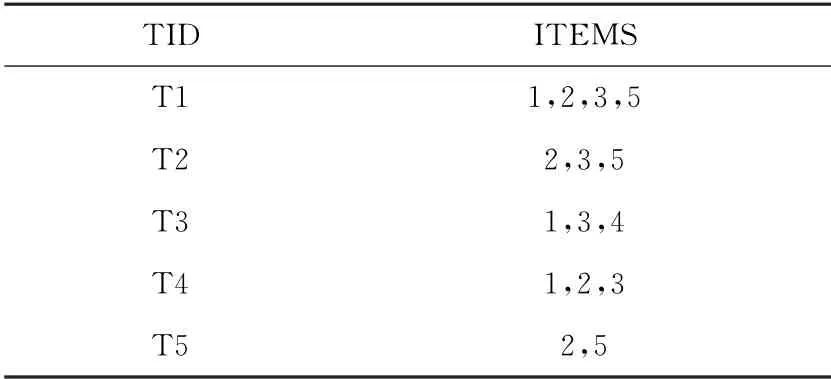
表1 实例的事务记录

表2 候选1-项集的持事务数

表3 编码后的项

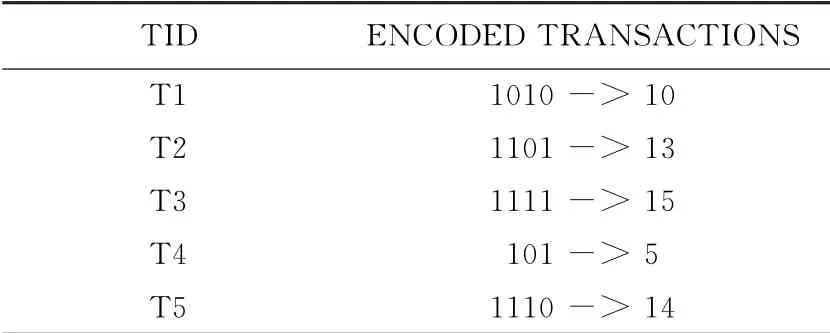
表4 编码后的事务记录

初始化频繁1-项集的节点之后，节点“3”二进制编码的结果对每个编码后的事务记录进行与运算。由性质3，如果dataset&1000＝1000，则节点“3”表示的项集是该事务记录的子集，从而可以将该事务记录添加到节点“3”包含的事务记录之中。可以得到节点“3”包含的事务记录有T1，T2，T3，T5。同理可得，节点“2”包含的事务记录有T2，T3，T4，T5。节点“1”包含的事务记录有T1，T3，T5。节点“5”包含的事务记录有T2，T3，T4。由于根节点含有“3”，“2”，“1”，“5”四个子节点，根据性质4 知道可以产生的候选2-项集为“32”，“31”，“35”，“21”，“25”，“15”。

统计候选项集‘32’的支持度需要遍历的事务记录为节点“3”包含的事务记录而不是所有的事务记录。由性质3可以知道，遍历事务记录的时候，与事务记录进行“与”运算即可。如果dataset&100＝100相等，说明该事务包含“32”，所以可以将该事务分配给节点“3”的子节点“32”。可以得到“3”的子节点“32”包含的事务记录为T2，T3，T5。同理可得“31”包含的事务记录为T1，T3，T5。“35”包含的事务记录为T2，T3。“21”包含的事务记录为T3，T5。“25”包含的事务记录为T2，T3，T4。“15”包含的事务记录为T3。由于节点“15”的支持度为0.2，小于最小支持度，去掉该节点。在统计候选项集的支持度的时候，节点“3”的子节点需要遍历的事务记录数量为4，节点“2”的子节点需要遍历的事务记录的数量也为4，节点“1”的子节点需要遍历的事务记录数量为3。

经过上述步骤的操作，节点“3”有三个子节“32”，“31”，“35”。所以由性质4，产生的候选3-项集为“321”，“325”，“315”。通过Apriori算法的性质2可知，“315”一定不是频繁项集，因为子集“15”为非频繁项集。判断“321”是否是频繁项集需要遍历的事务记录为节点“31”包含的事务记录T2，T3，T5。对每个事务记录的操作为dataset&10＝10。如果相等，则说明dataset包含“321”，可以获得的事务记录为T3，T5。同理可得“325”的事务记录为T2，T3。节点“2”有两个子节点“21”、“25”。所以产生的候选3-项集为“215”。由于该项集的子集“15”是非频繁项集，所以去掉该项集。在统计候选项集支持度的时候，节点“32”子节点需要遍历的事务记录数量为3。

通过节点“32”可以得到频繁3项集为“321”，“325”。由于节点“32”含有两个子节点，所以可以产生的候选4项集为“3215”，因为该候选项集包含有3-项集“315”，而“315”是非频繁项集，所以“3215”是非频繁项集。算法到此结束。

在挖掘频繁项集的过程中，需要统计支持度的候选项集为“3”，“2”，“1”，“4”，“5”，“32”，“31”，“35”，“21”，“25”，“15”，“321”，“325”。在使用Apriori或者FIMST 算法统计候选项集的支持度的时候，这些项集需要遍历的事务记录数量为13×5＝75，而使用本文算法的时候，需要遍历的事务记录数量为5×5＋4×3＋4×2＋3×1＋3×2＝54。所以本文算法减少统计候选项集需要遍历事务记录的比例为28%。因此通过给节点添加事务记录这个属性，可以有效的减少统计候选项集需要遍历的事务记录的数量，提高算法的执行效率。

频繁项集节点组成的排序树如图2所示，灰色填充的节点为非频繁项集节点。

2.3 算法描述

1)扫描事务记录，获取所有单个项集的支持度。剔除非频繁1-项集，并将频繁-1项集根据支持事务数按照从大到小的顺序排列；

2)对事务记录进行二进制编码；

3)初始化根节点，并为根节点分配孩子。根节点的孩子为所有的频繁1-项集。对根节点的每个孩子节点与事务记录进行“与”运算的方式分配事务记录；

4)根据每个频繁-1项集的兄弟节点为其分配候选2-项集的孩子节点。由于候选2-项集的所有子集都是频繁1-项集，所以不需要剪枝。对每个候选2-项集遍历其父节点包含事务记录，并与事务记录进行“与”运算的方式为候选项集节点分配事务记录，去掉含有的事务记录比例小于预先设定的支持度的候选项集节点；

5)根据每个频繁k-项集的兄弟节点为其分配候选(k＋1)-项集的子节点。利用Apriori算法性质2对子节点进行剪枝。对每个候选(k＋1)-项集遍历其父节点包含事务记录，并与事务记录进行“与”运算的方式为候选项集节点分配事务记录，去掉含有的事务记录比例小于预先设定的支持度的候选项集节点；

6)不断重复第5步，直到不能产生候选项集节点为止。

2.4 算法的性能分析

通过对频繁项集和候选项集以节点的方式进行组织，利用节点之间的关系，进行候选项集的产生和支持事务数的统计，从而提高算法的执行效率[21]。

1)避免了多次扫描数据库，仅仅扫描两遍数据库，就可以通过编码后的事务集代替数据库中的事务记录。之后仅仅通过在内存中的运算，就可以得到全部频繁项集。

2)根据性质1，可以利用二进制的运算代替此Apriori算法执行过程中的集合之间的运算。集合在编程语言中需要转化为特定的数据结构，再进行集合之间的运算。而二进制编码后的项集可以省略中间步骤，从而提高算法的执行效率。

3)根据性质2可以知道兄弟节点具有共同的前缀，不需要对所有频繁k-项集两两之间判断是否有相同(k-1)项来进行连接步骤了。在频繁k-项集的个数为n 时，连接步骤因为需要两两频繁k-项集的判断，所以时间复杂度为O(n2)，而在本文算法中省去了判断的步骤，因为兄弟节点的前缀都是相同的，兄弟节点直接连接就可以产生候选项集。

4)根据性质3，利用父节点代表的频繁项集是子节点代表的候选项集的子集的条件，可以减少统计子节点代表的候选项集支持度需要遍历的事务记录数量。给节点添加一个属性，表示包含该节点的所有事务记录。这样由于父节点是子节点的子集，那么只有在包含父节点的基础上，才可能包含子节点，这样可以遍历父节点的事务记录属性，获得子节点的所有事务记录属性。相当于在统计候选项集节点支持度时利用了统计父节点支持度的事务记录的结果，避免了每次统计候选项集支持度时，需要遍历所有事务记录。对于从根节点到任意一个叶子节点，每个节点包含的事务记录是非增的，这样随着候选项集节点深度越大，其需要遍历的事务记录数量越少。

3 实验验证

实验环境:处理器2.7 GHz Intel Core i5，内存8 GB 1867 MHz DDR3，操作系统mac OS 10.13.5，采用Python3.6作为开发语言，分别实现了基本的Apriori算法，FIMST 算法和Node-Apriori算法。实验数据采用的数据集为UCI Machine Learning Repository中的mushroom 数据集、chess数据集以及R 语言扩展自导的groceries数据集，这三个数据集经常被使用在关联规则算法实验中。实验目的是对比三种算法在mushroom 数据集、chess数据集以及groceries数据集上的表现。mushroom 数据集中的事务数为8124，事务的长度均为23，总共包含120个项。chess数据集中包括的事务记录数为3196，事务的长度均为36，虽然该数据集中的事务数较少，但是频繁规则较多，所以选择比较的支持度较大。groceries数据集是R 语言arules包自带的数据集，是某个杂货店一个月的真实交易记录，包含有9 835条消费记录和139个商品，该数据集中事务记录和事务项都较多，在支持度较小的时候对三种算法的运行时间才具有区分度。

图3、图4和图5分别表示三种算法在mushroom 数据集、chess数据集以及groceries数据集中的运行时间的折线图。

在支持度较小的时候，频繁1-项集会较多，由于算法是层层迭代的，所以造成之后的计算量增多，也就是算法的运行时间会随着支持度的增大而减少。从图3、图4和图5可知，Node-Apriori算法在支持度较小时，其运行时间均远小于另外两种算法；在支持度较大时，耗费时间也小于另外两种算法。随着支持度的减少，挖掘的关联规则越多，其他两种算法与Node-Apriori算法的差距就越大。而FIMST 算法虽说较Apriori算法有一定的提升，但是仅仅是在连接产生候选项集的过程中进行了优化，而算法在时间上消耗最多的过程当属于遍历事务记录统计候选项集的支持度[16]。算法Node-Apriori在FIMST 算法改进的基础上，给节点增加了事务记录这个属性，有效的减少了统计候选项集支持度需要遍历的事务记录数量，极大的提高了算法的执行效率。

对于mushroom 数据集在支持度为0.2的时候，统计得到三种算法在挖掘频繁项集的过程中产生的候选项集个数为54 522，对于候选项集Node-Apriori算法遍历的事务记录数量为124 558 694，而总的事务记录数量为8 214。可以得到相较于Apriori算法，Node-Apriori算法减少了遍历事务记录数量的比例为72%。这个比例对于3.2实例介绍的少了许多，是因为随着候选项集节点的深度的增加，统计其支持度的时候需要遍历的事务记录数越少。

注意，节点中可能包含重复数据。例如节点“3”包含的数据集为T1，T2，T3，T5。节点“2”包含的事务记录有T2，T3，T4，T5。两个节点都包含T2，T3，T5。这是因为事务记录中包含项2，也是可能包含项3的。并且，算法采用的是广度优先的搜索方式，生成候选项集，统计支持度，剔除非频繁项集。在数据量比较多的时候，由于每个节点包含的数据量包含重复的部分，对内存的消耗上还是比较大的。

4 结论

本文在FIMST 算法的基础上，利用频繁项集和候选项集以节点关系组织的形式，进行候选项集的产生，从而改进了Apriori算法的执行效率。Node-Apriori算法通过对事务记录进行二进制编码的方式编码事务记录，给频繁项集节点添加事务记录的属性，统计候选项集节点的支持度的时候，仅仅需要扫描候选项集父节点的所有事务记录即可。然后利用二进制编码的数据进行集合间的运算。有效的提高了算法的执行效率。但是同级节点之间包含可能相同的事务记录，在事务记录较多的时候，对内存的需求比较大。之后的工作可以就组织候选项集的方式上进行展开。