两个专属渔业资源区的离散动力学模型的分叉分析
2015-06-27顾恩国何秀川方自成
顾恩国,何秀川,方自成
(中南民族大学 数学与统计学学院,武汉 430074)
两个专属渔业资源区的离散动力学模型的分叉分析
顾恩国,何秀川,方自成
(中南民族大学 数学与统计学学院,武汉 430074)
对渔业资源储量-捕捞力度动态模型进行了进一步研究,运用中心流形定理及规范型分析了正平衡点在flip分叉及Neimark-Sacker分叉时的临界稳定性,并用数值模拟验证了所得的理论结果.
flip分叉;Neimark-Sacker分叉;中心流形定理;规范型
随着人口增长和经济快速发展,生态系统中资源的过度捕捞已严重影响其再生能力和人类对它的可持续利用,因此生态系统的可持续发展成为人们关注的焦点,而渔业资源的可持续发展便是其中一类典型问题[1,2].在国内外,关于渔业资源可持续发展,许多学者已经建立大量数学模型对其进行研究[3-6],关于不同区域的生物经济模型有一些,大多为ODE模型[7,8],由于渔业捕捞作业以离散行为为主,利用离散动力系统理论研究不同类型的渔业资源[9]或者不同类型的捕捞作业[10]对渔业资源系统的影响,调控系统避免过度捕捞造成资源枯竭等问题逐渐受到专家学者的亲睐,文献[11]提出了一类具有两个专属渔业资源区的渔业资源捕捞模型,并对其进行局部稳定性分析和全局分析.众所周知,分叉分析能够揭示分叉参数发生变化时,系统表现出的丰富动力学现象,而flip分叉是通往混沌的典型道路,Neimark-Sacker分叉会由于准周期波动产生不变闭曲线,因此本文研究文献[11]中模型的正不动点在发生flip分叉和Neimark-Sacker分叉时的临界稳定性,进一步完善对文献[11]中系统动力学现象的认识,为渔业资源控制系统的研究打下坚实的基础.
1 预备知识
考虑文献[11]中的渔业资源储量-捕捞力度动态模型:
(1)

根据(1)式,该模型可写成映射动力系统形式:
(2)

系统(2)的稳定性主要取决于系统(2)的Jacobian矩阵的特征值,该矩阵在平衡点(x,E)有如下形式:




通过简单的计算,我们获得以下定理1.
定理1 (1)不管参数c,p,r,K,Q如何变化,系统(2)边界平衡点E0(0,0)都是不稳定的鞍点.


2 正平衡点产生flip分叉时的稳定性

首先,正平衡点P可以通过以下变换转换到原点O(0,0):
系统(2)可以转换为:
(3)


(4)
其中
由中心流形理论可知,系统(4)存在一个中心流形,可表示为:
Mc={(x,y)∈2|y=h(x),h(0)=h′(0)=0,|u|<δ}.
(5)
δ表示一个足够小的正常数.
根据中心流形的定义,令y=h(x)=αx2+βx3+O(x4),则有:
g(x,h(x))=0.
(6)
通过方程(6)计算系数α,β,可以得到:
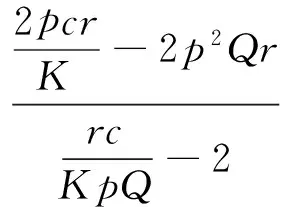

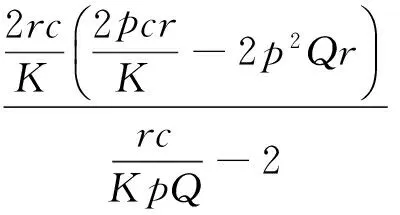


4r2c3p+3p2Q2K2-4p2r2c2KQ-96prcKQ<0,则有:

3 正平衡点产生Neimark-Sacker分叉的临界稳定性


此时,矩阵JP的一对共轭复特征值为:

a1±iA.
(7)


(8)
计算方程

(9)

(10)





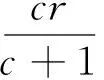
我们可以求得临界实部:

C1(a2a4-b2b4)+C2(a2b4+a4b2)-
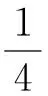

综合上述分析,通过Neimark-Sacker分叉理论,得到定理3.

(1) 如果d(0)<0,在非平凡不动点P处分支出唯一稳定的闭不变曲线(ICC);
(2) 如果d(0)>0,不动点P是稳定的.
4 数值模拟




图1 系统(2)关于环境存载能力K的分叉图,浅色线代表捕捞力度,深色线代表鱼的密度Fig.1 The bifurcation diagrams of the system (2) with respect to environmental carrying capacity K, fishing intensity is represented in light line, and the density of fish is represented in dark line

图2 从不动点P分叉出的唯一稳定ICCFig.2 An unique and stable ICC bifurcated from the fixed point P
5 结语与展望
本文研究了两个专属渔业资源区渔业资源的离散动力学模型,并对模型进行了非线性动力学分析,分别利用中心流形定理及规范型理论就系统的正不动点在发生flip分叉及Neimark-Sacker分叉时的临界稳定性进行了探究,探索了捕捞力度及鱼的密度与存载能力K的动态关系,一定程度上反映了渔业资源可持续利用的内在规律.
本文只考虑了动力学模型的局部稳定性及分叉现象,并未对系统进行全局分析及产生的混沌作进一步分析,这些都可以在以后的工作中进一步研究.
[1] Food and Agriculture Organization. The state of world fisheries and aquaculture[R]. Sofia:FAO, 2004: 22-25.
[2] Garcia M, Graiger J R. Gloom and doom? the future of a marine capture fishery [J].Philosophical Transitions of Royal Society, 2005, B360: 21-24.
[3] Bischi G I, Szidarovszky F. Harvesting dynamics in protected and unprotected areas [J]. Journal of Economic and Organization, 2007, 62: 370-384.
[4] Bischi G I, Kopel M, Szidarovszky F. Expectation-stock dynamics in multi-agent fisheries [J].Annals of Operations Research,2005, 137:299-329.
[5] Mckelvey R. Game theoretic insight into the international management of fisheries [J]. Natural Resourse Modeling,1997, 10: 129-171.
[6] 顾恩国,陈宝香. 有部分个体合作的多个体博弈公共渔业资源的非线性动力模型分析[J]. 中南民族大学学报:自然科学版, 2008,27(3): 96-101.
[7] Mchich R, Auger P M, Bravo de la parra R, et al. Dynamics of a fishery on two fishing zones with fish stock dependent migrations: aggregation and control [J]. Ecol Model, 2002, 158: 51-62.
[8] Mchich R, Charouki N, Auger P M, et al. Optimal spatial distribution of the fishing effort in a multi fishing zone mode [J]. Ecol Model, 2006, 197: 274-280.
[9] 顾恩国,陈 博,张梅娜. 带有红树林自然保护区的渔业资源动力学模型的局部分析[J]. 中南民族大学学报:自然科学版, 2013, 32(3): 104-107.
[10] 顾恩国,褚青涛. 不同理性两个体捕捞公共渔业资源的非线性分析[J]. 中南民族大学学报:自然科学版, 2009, 28(2): 109-118.
[11] 顾恩国,梁 艳. 两个专属渔业资源区的离散动力学模型分析[J]. 中南民族大学学报:自然科学版,2011, 30(1): 105-108.
[12] Saber N E. Discrete chaos [M]. New York: Chapman Hallcrc, 2000: 24-26.
[13] 尤里·阿·库兹涅佐夫. 应用分支理论基础[M].金城桴,译.北京:科学出版社,2009: 122-129.
Bifurcation Analysis of Discrete Dynamical Model for Two Special Fishery Resource Zones
GuEnguo,HeXiuchuan,FangZicheng
(College of Mathematics and Statistics,South-Central University for Nationalities,Wuhan 430074,China)
In this paper, we study the fish resources stock-effort dynamical model, analyse the marginal stability of positive fixed point at flip bifurcation and Neimark-Sacker bifurcation with center-manifold theorem and normal form respectively, and use numerical simulations to verify the conclusions.
flip bifurcation; Neimark-Sacker bifurcation; center-manifold theorem; normal form
2015-07-13
顾恩国(1964-),男,教授,博士,研究方向:非线性动力学应用,E-mail:guenguo@163.com
国家自然科学基金资助项目(61374085);中南民族大学研究生创新基金资助项目(2015sycxjj130)
O193
A
1672-4321(2015)03-0105-06
