大直径盾构隧道开挖面失稳极限平衡分析

吴为义，李凤涛

(1.浙江交通职业技术学院，杭州 311112；2. 浙江大学 建筑工程学院，杭州 310058)

大直径盾构隧道开挖面失稳极限平衡分析

吴为义1，李凤涛2

(1.浙江交通职业技术学院，杭州 311112；2. 浙江大学 建筑工程学院，杭州 310058)

近年来大直径隧道在国内外得到越来越多的应用，随之带来的开挖面稳定性问题也受到越来越多的关注，其关键是开挖面支护压力的大小。通过对三维楔形体模型进行修正并采用极限平衡分析方法，推导出适于大直径盾构隧道开挖面局部稳定性问题的理论计算公式。通过对理论公式的分析，存在楔形体最优破坏角及开挖面极限支护压力，分析了楔形体最优破坏角与局部失稳率、土体内摩擦角和隧道覆土厚度的关系，以及开挖面极限支护压力与土体内摩擦角和隧道覆土厚度的关系。

大直径隧道；开挖面；局部失稳；极限平衡分析；支护压力

大直径盾构隧道具有运能、经济及空间利用等方面的一系列优势，近几年在杭州，上海，南京及武汉等地的水下隧道建设中得到了广泛应用。在大直径盾构隧道掘进过程中，选择合理的开挖面支护压力是设计与施工中的一个难题，不合适的开挖面支护压力会对周围环境产生比较大的影响。近年来开挖面失稳事故在上海、广州、深圳盾构隧道中均有发生[1]。因此，确定合理的开挖面支护压力在设计与施工中非常必要。

当前针对开挖面支护压力已有不少的理论和实验研究。Davis等[2]基于Broms提出的稳定系数法，采用上限塑性极限分析及开挖面破坏机理提出了开挖面的下限解。在Davis的研究基础上，Leca和Dormieux[3]提出圆锥形块体的圆弧滑动面失稳模式，并建立了三维极限分析法获得了极限支护压力的上下限解。Mollon等[4]进一步采用多块体极限分析上限法获得了更优的上限解。基于筒仓理论，Jancsecz[5]建立了三维楔形体模型，并将其引入隧道开挖面稳定性的研究。Anagnostou[6]基于该法进一步研究了隧道施工中地下水渗流产生的渗透力对极限支护压力的影响。Li[7]基于极限分析方法和三维数值计算对上海长江隧道进行了分析，指出在设计与施工过程中必须考虑大直径隧道的开挖面局部稳定性问题。对于大直径隧道而言，盾构开挖面失稳更容易发生局部失稳模式，因此继续沿用传统的针对中小直径隧道的方法来分析大直径隧道开挖面稳定性就存在着较大的局限性。文中拟通过修正三维楔形体模型来计算大直径隧道开挖面局部失稳的支护压力。

1 三维楔形体极限平衡分析

楔形体计算模型假定开挖面失稳破坏形状由开挖面前方的楔形体(A′B′CDFE)和上部的棱柱体(CDFEGHJI)两部分组成，如图1所示。文中提出的修正楔形体模型包括上部棱柱体(CDFEGHJI)和开挖面前方楔形体(ABCDFE)。棱柱体宽度D为盾构隧道直径 ，棱柱体高度C为隧道埋深，为楔形滑块与开挖面的夹角，L为局部失稳高度(楔形体高度)。定义开挖面局部失稳比率为β=L/D。γ为土体重度，φ为土体的内摩擦角，c为土体的粘聚力。

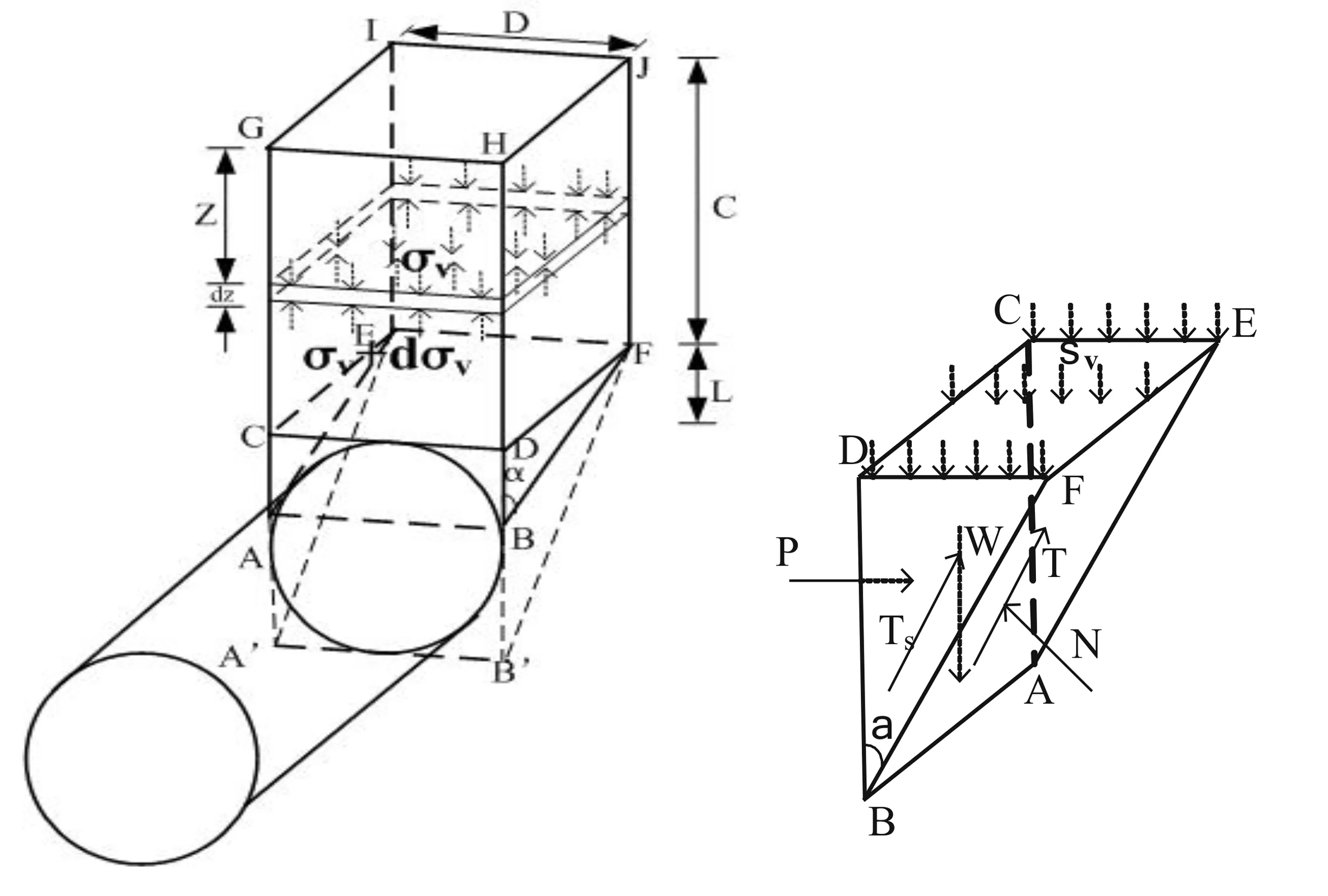
图1 修正楔形体极限平衡模型分析图

采用三维空间中的太沙基松动土压力理论，筒仓侧面上的水平应力与竖向应力的比值k=1-sinφ，上覆土平均土压力为συ，上覆土内任一dz范围土柱单元的竖向受力平衡为：

συβD2tanα+tanαγβD2dz-

2(D+βDtanα)τdz=βD2tanα(συ+dσυ)

(1)

τ=c+κσυtanφ，带入可得：

(2)

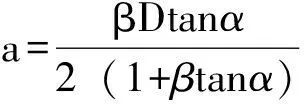
引入边界条件为，解得棱柱体任意深度z处的松动土压力为：

(3)

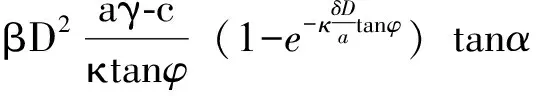
(4)

(5)

楔形体侧面的法向力为：

(6)

楔形体侧面的摩擦力为：

(7)

楔形体自重为：

(8)

楔形体前端滑裂面法向摩擦力T为：

(9)

竖直方向楔形体受力平衡方程为：

Pv+W-2Tscosα-Tcosα-Nsinα=0

(10)

水平方向楔形体受力平衡方程为：

P+2Tssinα+Tsinα-Ncosα=0

(11)

联立式(3)-(11)，可得出维持开挖面稳定的总支护力P为：

(12)

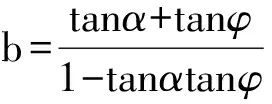
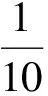
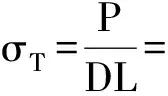
(13)

2 极限支护压力分析

由式(13)可知，支护压力σT主要受楔形体几何参数(D，C，α)，土体参数(φ，c)和局部失稳率β的影响。本节采用大直径隧道D=10m，C/D=1.0，土体内摩擦角φ为30°，黏聚力为0.1kPa，局部失稳率β=0.5进行极限支护压力分析。图2给出了由文中修正楔形体模型得出的维持开挖面稳定的极限支护压力与土体内摩擦角的变化规律，并与其他解析解得到的极限支护压力结果进行对比。可以看出，由文中解、Anagnostou解和Leca解得出的支护压力随着内摩擦角的变化规律均相同。Anagnostou解将开挖面作为整体失稳来处理，实际上大直径隧道开挖面失稳则为局部失稳，因此Anagnostou解均大于文中解和Leca解。当内摩擦角小于30°时，文中解小于Leca解；当内摩擦角大于30°时，两解则趋向于比较接近。计算结果对比表明，文中解能够比较准确地计算支护压力，而且由于修正楔形体公式比较简便，利用本文解来计算开挖面支护压力具有很好的优势。

图2 计算结果对比(D=10m, C/D=1.0，β=0.5)

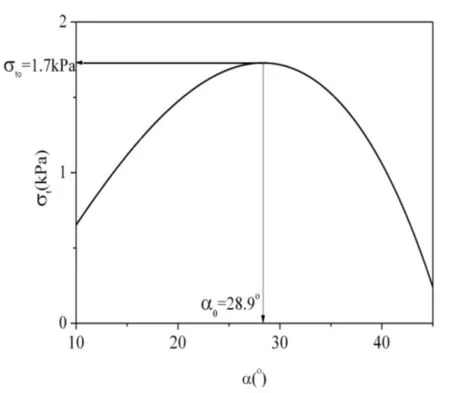
图3 σTo～α(φ=30°, C=0.1kPa)

图3为楔形体支护压力随α变化的关系，当α等于28.9°时，σΤ取最大值1.7kPa，意味着当支护压力小于1.7kPa时，有可能发生开挖面失稳的现象。此时的支护压力是开挖面的临界支护压力，定义此时的夹角为最优破坏角αo，此时的支护压力为开挖面极限支护压力σTo。

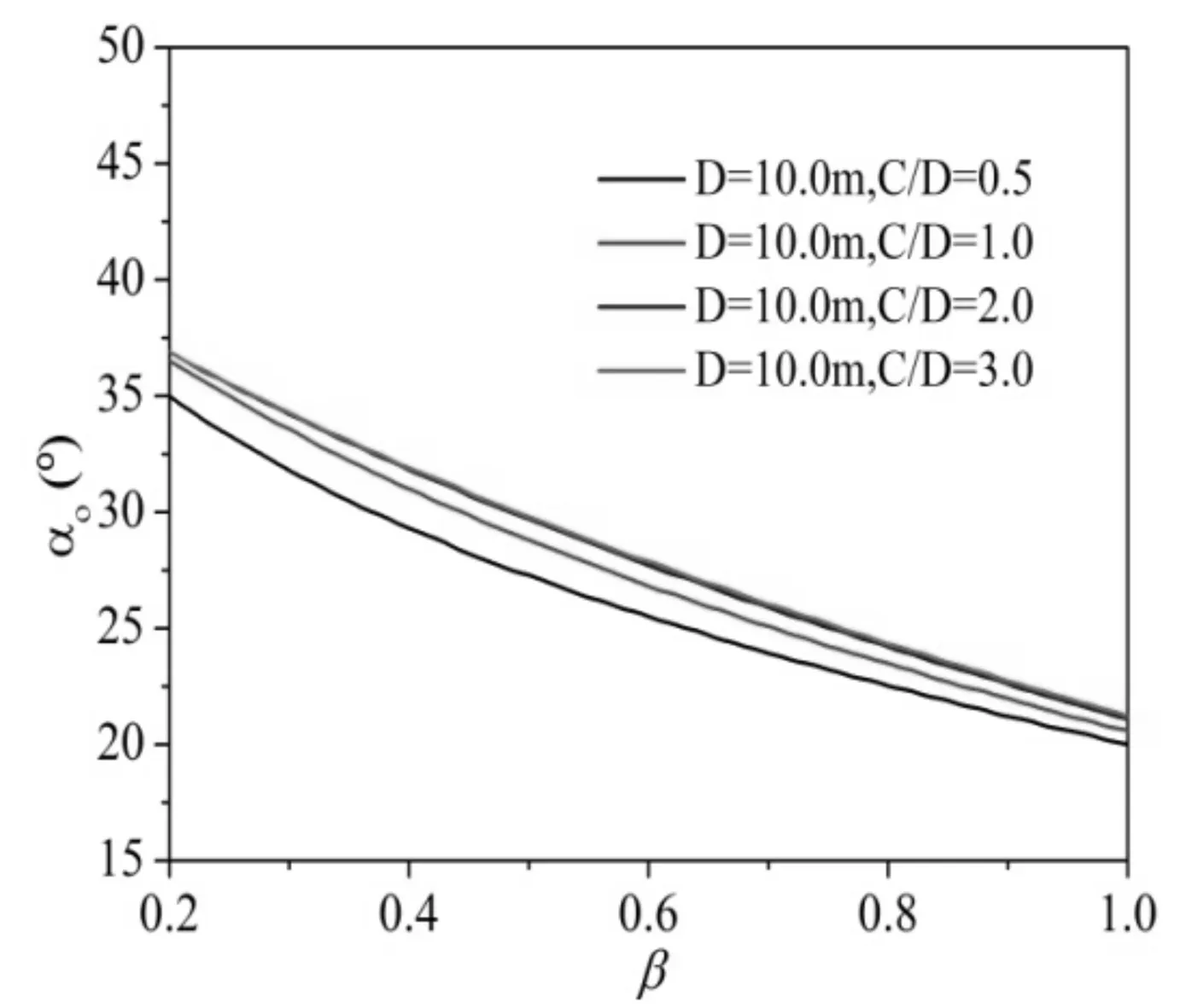
图4 αo～β(φ=30o, C=0.1kPa)

图

图4为最优破坏角αo和开挖面局部失稳比率的关系。当C/D=1.0,β=0.2时，αo=36.5°；当β增大到1.0时，αo则减小到20.6°。随着β逐渐增大，αo逐渐减小且大致呈线性递减关系，这说明β是影响αo的重要因素。对应于不同的C/D，均呈现出相同的规律。随着C/D的逐渐增大，C/D对最优破坏角影响不大，最大相差约3°。

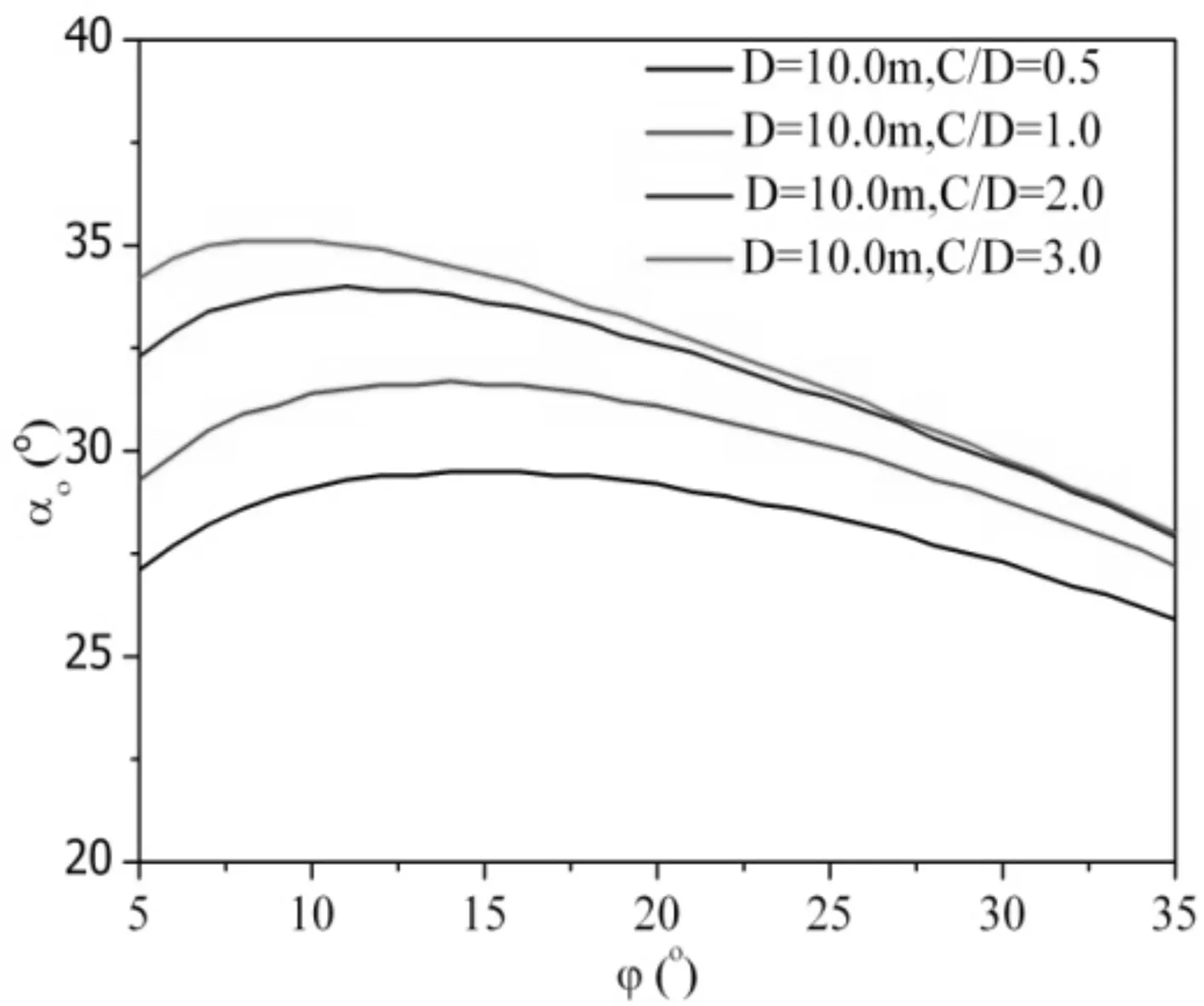
随着土体的内摩擦角φ的变化，αo的变化规律如图5所示。随着φ的逐渐增大，αo表现出先增大后减小的趋势。如对于C/D=1.0工况，当φ=5°时，αo=29.3°；当φ=15°时，αo=31.6°；当φ=40°时，αo=25.5°。对于相同的C/D，αo最大值与最小值相差约6°。对于相同的土体内摩擦角φ=10°，随着C/D的逐渐增大，αo也逐渐增大(当C/D=0.5时，αo=29.1°；当 C/D=3.0时，αo=35.1°)，这说明在局部失稳率相同时，土体的内摩擦角和C/D对最优破坏角均有影响。

图6为支护力随土体内摩擦角变化的规律。随着φ增大，σTO逐渐减小。以C/D=1.0为例，当φ=5°时，σTo=5.4kPa；当φ=30°时，σTo=1.7kPa。对比可见，随着C/D增大，σTo也随着增大，但当φ大于30°以后，不同C/D对应的极限支护力基本相同。可以看出，土体内摩擦角对极限支护压力有着较大的影响；当内摩擦角小于30°时，不同的C/D对极限支护力有一定的影响。

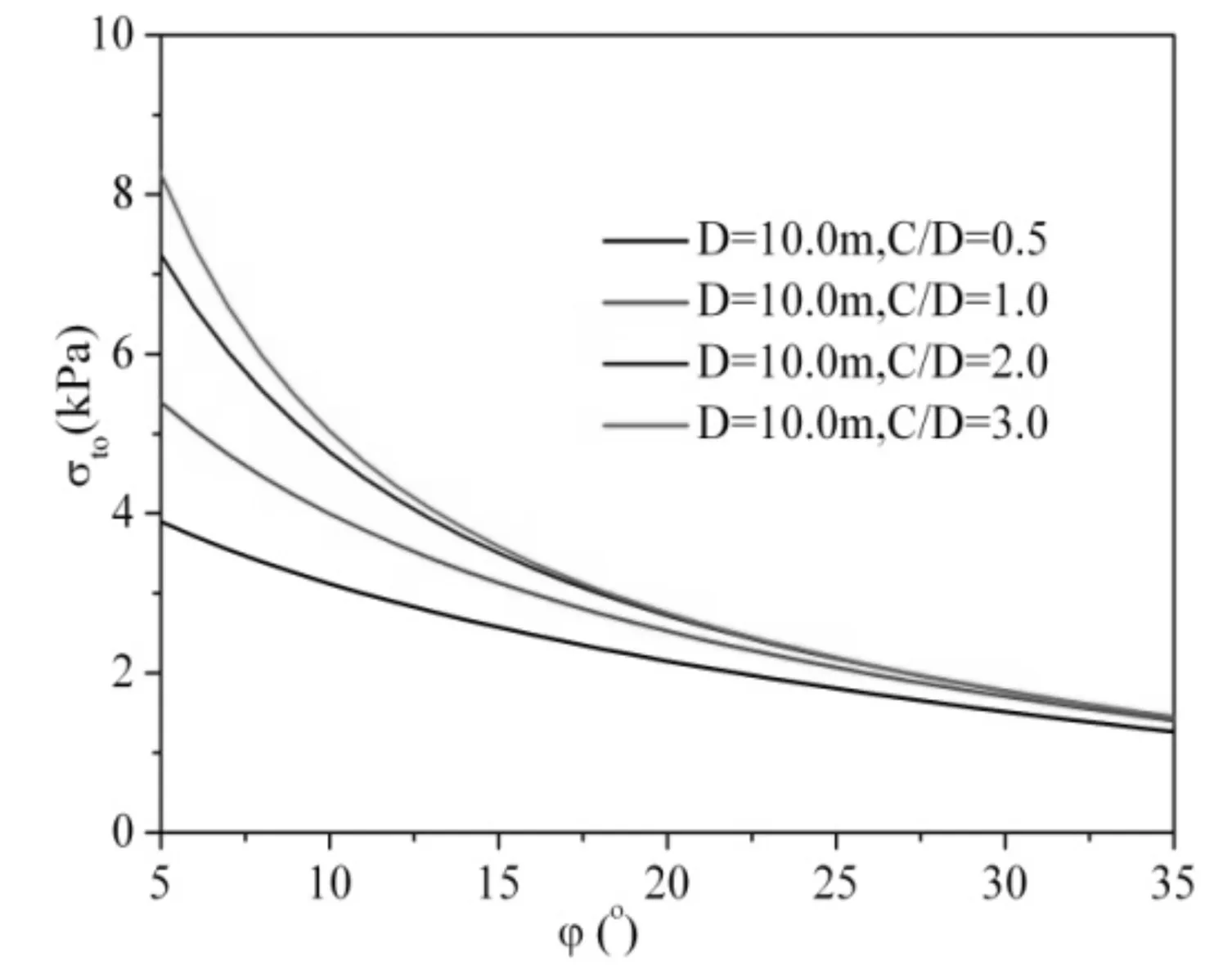
图6 σTo～φ(C=0.1kPa，β=0.5)

3 结 语

基于三维修正楔形体模型采用极限平衡分析方法得出了开挖面局部失稳理论计算公式，与Anagnostou解和Leca解对比表明，该公式在计算大直径盾构隧道时非常简便，而且比较准确。极限支护压力主要受楔形体几何参数、土体参数和局部失稳率的影响。最优破坏角主要受开挖面局部失稳比率、土体内摩擦角影响；覆土层厚度对最优破坏角则影响不大。极限支护压力随着内摩擦角的增大逐渐减小，当内摩擦角大于一定值时，覆土厚度对极限支护压力几乎不产生影响。

[1]竺维彬，鞠世健. 地铁盾构施工风险源及典型事故的研究[M]. 广州：暨南大学出版社，2009.

[2]Davis E H, Gunn M J, Mair R J. The stability of shallow tunnels and underground openings in cohesive material[J]. Géotechnique，1980, 30(4): 397-416.

[3]Leca E. Dormieux L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material [J]. Géotechnique，1990, 40(4): 581-606.

[4]Mollon G, Dias D, Soubra A-H. Face stability analysis of circular tunnels driven by a pressurized shield [J], Journal of Ceotechnical and Geoenvironmental Engineering，2010, 136(1): 215-229.

[5]Jancsecz S, Steiner W. Face support for a large mix-shield in heterogeneous ground conditions[C]// Symposium Tunnelling 94. London: Chapman and Hall Limited，1994: 531-550.

[6]Anagnostou G, Kovari K. The face stability of slurry shield-driven tunnels[J]. Tunnels and Underground Space Technology，1994,9(2): 165-174.

[7]Yun Li, F. Emeriault, R. Kastner, et al. Stability analysis of large slurry shield-driven tunnel in soft clay[J]. Tunnels and Underground Space Technology，2009,24(2): 472-481.

Limit Equilibrium Analysis of the Face Instability in Large Diameter Shield Tunnels

WU Wei-yi1,LI Feng-tao2

(1. Zhejiang Institute of Communications, Hangzhou 311112, China;2. College of Civil Engineering and Architecture, Zhejiang University , Hangzhou 310058 , China)

Large diameter shield tunnels are widely constructed in recent years. Tunnel face stability is one major concern for setting a proper support pressure. The traditional model of wedge for stability analysis of tunnel face is extended to encompass large diameter tunnels on the partial face instability adopted by limit equilibrium methods. It is founded that there is the optimal angle between the working face and the wedge and the limit support pressure. The relationship between the optimal angle and ratio of partial face instability, soil internal friction angle, cover-depth ratio are demonstrated. The relationship between the limit support pressure and soil internal friction angle, cover-depth ratio are also shown. The results are compared with Anagnostou’s solution and Leca’s solution, which reveal that the results are suitable for the face stability of large tunnels.

large diameter shield tunnels; working face; partial face instability; limit equilibrium analysis; support pressure

2015-11-16

浙江省交通运输厅科研计划项目(2013H26)

吴为义(1975- )，男，安徽舒城人，副教授，E-mail：wuweiyi2002@163.com。

U455.43；U456.1

A

10.3969/j.issn.1671-234X.2015.04.006

1671-234X(2015)04-0024-04