中主应力对原状软粘土强度与变形影响的试验研究

王月梅

(江西理工大学应用科学学院，江西 赣州 341000)

中主应力对原状软粘土强度与变形影响的试验研究

王月梅

(江西理工大学应用科学学院，江西 赣州 341000)

赣南地区软粘土层性状复杂，强度低、孔隙比大、压缩性高、结构性强，而土体的原生各向异性及次生各向异性使影响强度、变形的因素更复杂。借助空心圆柱扭剪仪(HAC)从应力-应变关系的角度研究赣南原生粘土土体不同中主应力参数及主应力轴旋转下的变形规律。试验数据显示原状软粘土土体应变随大主应力轴偏转角增大呈渐增趋势，达到最大值45°后呈渐低趋势；各向应力值未因主应力轴旋转有明显改变，但旋转会产生应变累积；中主应力系数b=0.5时土体原生各向异性在径向应变上有更明显反应。

中主应力系数；主应力方向；各向异性；主应力轴旋转；原状软粘土

0 引 言

赣南地区广泛分布着深厚的软粘土层，随着交通建设的迅速发展，软粘土层的土动力学和岩土工程方面的问题也大量产生，比如复杂交通荷载引起的地基动应力和粘土地基沉降变形。由于粘土的原生异向特性与砂土、粉土等土体有着明显不同，荷载的作用使得土体产生更复杂的次生各向异性，因此，在建设路桥，高铁等交通设施过程中，动荷载对性状复杂的软粘土层结构、强度与变形等的影响成为项目规范、设计、施工和安全等方面需要解决的关键问题。为此，进行了原状软粘土主应力轴旋转条件下应力应变特性的试验研究，通过试验分析交通荷载下中主应力系数对原生各向异性粘土土体中应变与强度的影响。

1 试验方案

1.1 试验试样及样品

文中选用空心圆柱仪(HCA，Hollow Cylinder Apparatus)为广州欧美大地仪器设备有限公司的 SS-HCA，来自英国GDS公司。SSD-HCA仪可以提供四个加载参数以及内外围压四个应力加载参数；相比常规三轴仪，直剪仪等，SSD-HCA仪可更好地研究中主应力、大主应力方向角等对粘土层应力应变特性的影响。试样固结前采用反压饱和法，分级施加围压与反压来压缩溶解试样内含气体，确保试样饱和。土样和试样制备、固结试验参考我国行业标准《土工试验规程》。

试验用土采用取自赣州某工地的原状粘土。取土深度在地面以下约7.5m处，地下水位于地面以下1.5m。孔隙比е=1.79；含水率w =54.8%；比重G=2.74；湿密度ρ=1.87g/cm3；饱和度98.6%。土样制备成 200mm×100mm×60mm(高度×外径×内径)的空心圆柱试样，如图1(a)所示。空心圆柱试样在HCA压力室中施加反压50kPa饱和，饱和之后根据试样土的现场埋置深度施加200kPa的围压(有效围压P=150kPa)等向固结，使其超固结比OCR接近l。

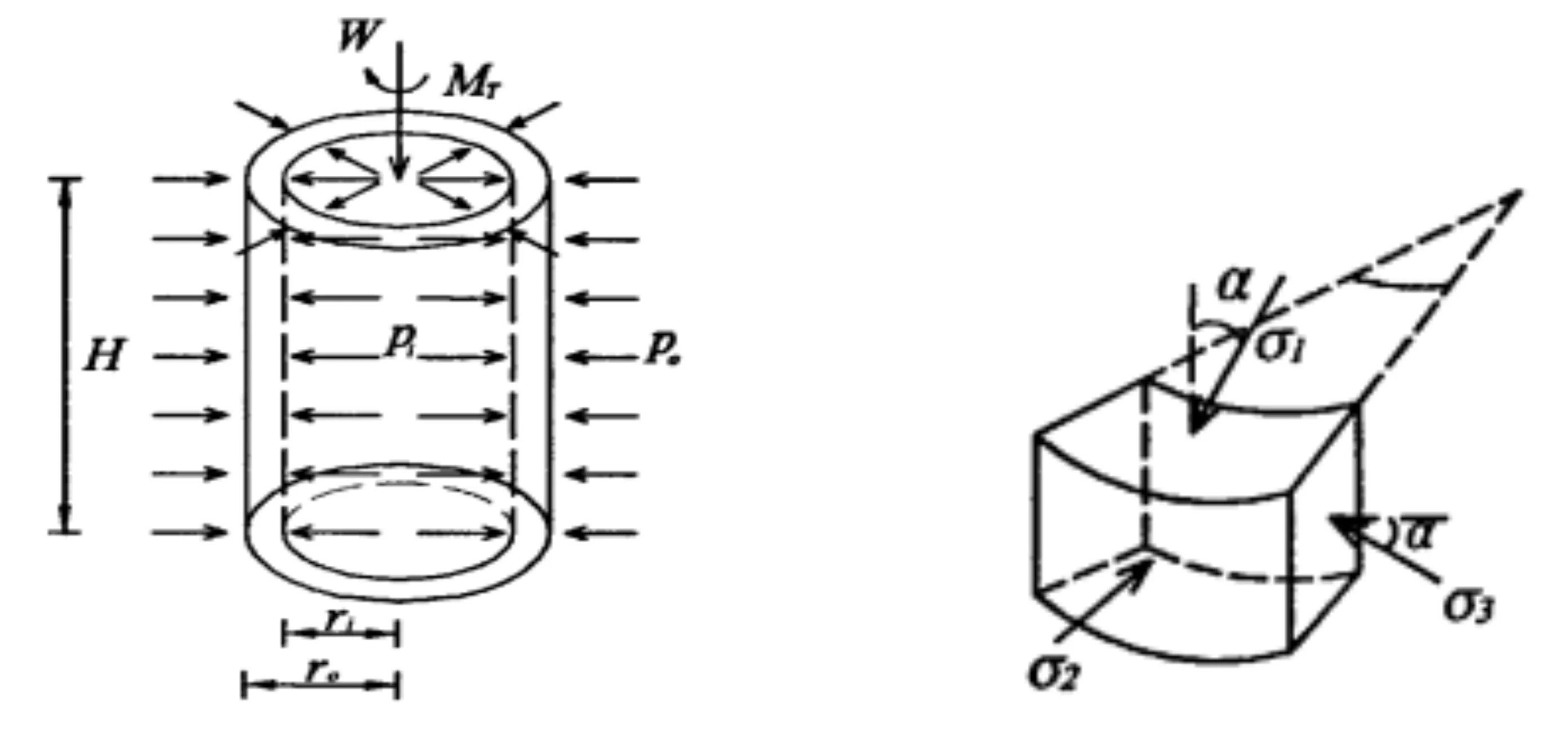
(a)W—轴力；Mr—扭矩；Po—外压；Pi—内压 (b)σ1—大主应力；σ2—中主应力；σ3—小主应力；α—大主应力轴偏转角

1.2 试验加载方案

按照《土工试验规程》取1h排水量不超过0.1cm3作为固结标准使土样完成固结后预备下列试验。 (1)在保持中主应力方向不变情况下，设计了粘土土体在不同主应力轴方向下的定向剪切应力应变试验。荷载过程中保持大主应力轴偏转角α、平均总主应力P、中主应力参数b值不变的条件下，改变剪切应力q值直至试样破坏。定向剪切应力应变试验在有效等向围压150kPa(外压200kPa，内压200kPa，反压50kPa)下，选取大主应力轴偏转角α 分别为0°、20°、35°、60°、80°等5个方向进行，如表1所示；(2)地基粘土层在低频动荷载过程中，土体主应力轴经常发生旋转，故设计了主应力轴旋转下的剪切试验。荷载过程中保持平均总主应力P、中主应力参数b值不变的条件下，按预设应力路径改变大主应力轴偏转角α、剪切应力q值直至试样破坏，如表2所示。

试验中的平均总主应力P=(σ1+σ2+σ3)/3=150kPa，σ1、σ2、σ3分别表示大、中、小主应力，如图1(b)所示；剪切应力q=(σ1-σ3)/2；中主应力系数b=(σ2-σ3)/(σ1-σ3), b∈[0, 1]，试验选取b=0，0.5。通过不同中主应力系数下的剪切试验，观察试验样品的应力-应变关系曲线，研究中主应力系数b值对粘土土体应变和强度的影响[1-2]。

表1 定向剪切试验方案

表2 主应力轴旋转剪切试验方案

2 试验结果及分析

基于文中的研究目标，软粘土土体的应力-应变特性是考察的重点，即从三个主应力{σ1，σ2，σ3}方向上的应变{ε1，ε2，ε3}及其随应力增长的变化分析粘土土体各向异性下的变形情况。由HCA的相关原理知[3-4]，各应变的对应关系如下：

(1)

(2)

ε2=εr

(1)根据直流系统接地报警，关键是尽快查出接地性质与接地支路。正常运行时，正极对地电压为110V，负极对地电压为-110V。当发生单点非金属性接地时，相应正极或负极对地电压降减少，另一负极或正极对地电压升高，例如：当正极对地发生单点非金属性接地时，则U+﹤110V、U-﹥110V，据此，判断故障性质为正极单点接地。当发生单点金属性接地时，相应正极或负极对地电压为零，另一负极或正极对地电压为220V，例如：当正极对地发生单点金属性接地时，则U+=0V、U-=-220V，据此，判断故障性质为正极单点接地。

(3)

式中，ε1，ε2，ε3为大、中、小主应变；εz，εr，εθ为试样在轴向、径向、切向上的应变，γzθ为扭剪应变。+ε表示压应变，-ε表示拉应变。

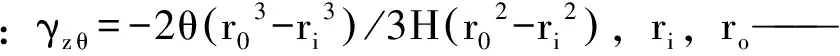
2.1 定向剪切应力应变试验及分析

定向剪切应力应变试验T 11～T 15(b=0)与T 21～T 25(b=0.5)，采用MATLAB对数据进行分析结果如图2～5所示。试验中以大小主应力之差的半值q(q=(α1-α3)/2)作为剪应力控制条件，因此图中以q作为应力应变关系图的应力纵坐标，横坐标为轴向、径向、环向应变及扭剪应变。

(1) 轴向应力-应变

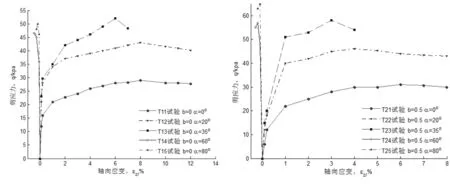
图2(a) b=0 定向剪切试验轴向应变应力图 图2(b) b=0.5定向剪切试验轴向应变应力图

图2(a)、图2(b)中显示了空心试样定向剪切试验的轴向应力-应变关系。这两图中随大主应力轴偏转角α的增长，空心试样产生同等轴向应变下剪应力呈递增趋势；而当大主应力轴偏转角α的增长大于45°时情况却相反。对比两图应力应变曲线，在施加荷载直至破坏的全阶段，T1(b=0)组试验的应变增长趋势都始终大于T2(b=0.5)组试验。

从曲线可以看出，在大主应力轴偏转角α<45°(α=0°，α=20°，α=35°)时T1组试验中空心试样的临界破坏轴向应变基本在6%～12%的范围之间；受中主应力参数b的影响，在T2组试验中，同一大主应力轴偏转角下T2(b=0.5)组试验的临界破坏轴向应变都要小于T1(b=0)组试验，各个方向上的临界破坏轴向应变则基本在4%～8%的范围之间。同时从曲线可见，当轴向应变达到1%～4%左右，即应变产生的初始阶段时，试样的强度已经逼近临界破坏应力。在两个曲线图都可明显看出，在主应力轴方向小于45°(α<45°)的时候，随着角度增大，破坏时的临界轴向应变值都随之减小。根据广义虎克定律，随着主应力轴偏转角增大，试样所受的轴向应力将减小，而轴向应变也将减小，试验情况与它是相符合的。

从曲线可以看出试样大主应力轴偏转角α>45°时，T1组试验中各方向的临界破坏轴向应变基本在-0.3%～-O.6%的范围之间变化；而受中主应力参数b的影响，T2组试验中，同一方向时T2的临界破坏轴向应变要略小于T1组试验，在各个方向上破坏时的临界轴向应变则基本在-0.1%～-O.3%的范围之间变化。在主应力轴方向大于45°(α>45°)的时候，随着大主应力轴偏转角增大，其破坏时候的临界轴向应变的值都随之增大，这与大主应力角度小于45°(α<45°)明显不同。

中主应力系数对软粘土试样的轴向应力-应变关系有影响，数值上处于同一数量级，因此效果并不显著。

图3(a) b=0 定向剪切试验径向应变应力图 图3(b) b=0.5定向剪切试验径向应变应力图

图3(a)、图3(b)中显示了空心试样定向剪切试验的径向应力-应变关系。对比两图应力应变曲线可以看到，相同大主应力轴偏转角下，T2组试验的临界破坏径向应变要小于T1组试验且多为负值(拉应变)，随角度大于45°时(α=80°)时临界破坏径向应变成为正值(压应变)。图中都能明显观察到，T1中其值基本都在-6%～-9%之间，而在T2中，试样的临界破坏径向应变基本在-0.4%～-0.5%及0.9%～1%之间。从图3(a)中可以看到随着大主应力轴偏转角增大，T1组试验空心试样在各个方向上的破坏临界径向应变值有明显减小趋势，而大主应力轴偏转角大于45°(α>45°)时，情况明显相反。从图3(b)可以看到随着大主应力轴偏转角增大,T2组试验空心试样在各个方向上的临界破坏径向应变值由负值(拉应变)朝着正值(压应变)变化，情况更加复杂。显然，T2组试验(b=0.5)规律性明显弱于T1组试验(b=0)，且T1组试验中临界破坏径向应变值明显要高于T2组试验。

中主应力系数对软粘土试样的径向应力-应变关系影响显著。

(3) 切向应力-应变

图4(a) b=0 定向剪切试验切向应变应力图 图4(b) b=0.5 定向剪切试验切向应变应力图

图4(a)、图4(b)中显示了相同b值不同大主应力轴偏转角上空心试样定向剪切试验的切向应力-应变关系。由应力应变关系曲线图中可以看到，各个方向上切向应力-应变曲线走势总体相似，T1组的破坏时临界切向应变值要大于T2组，但仍处于同一数量级。

由切向应力-应变关系曲线可以看出，T1、T2组试验的切向应变值都随大主应力轴偏转角角度增长而减小。在大主应力轴偏转角α<45°时，其破坏临界应变值随角度的增长而减小，切向应变为负值(拉应变)，T1组试验的临界破坏切向应变值基本在-4%～-6%之间，而T2组试验的值基本在-1%～-4%之间；大主应力轴偏转角α>45°时，切向应变为正值(压应变)，随角度变化的规律性不显著，T1组试验的临界破坏切向应变值基本在1.5%～4%之间，而T2组试验则在0.5%～3%之间，数值基本处于同一数量级。从图中T13、T14与T23、T24四条曲线的比较情况来看，在大主应力轴偏转角接近45°时候，切向应力会达到最大值qmax，与试验结果相符合。

由上述分析可以认为，中主应力参数b对于切向应变的影响不大。

(4) 扭剪应力-应变γZθ

图5(a) b=0 定向剪切试验扭剪应变应力图 图5(b) b=0.5定向剪切试验扭剪应变应力图

图5(a)、图5(b)中显示了空心试样定向剪切试验的扭剪应力-应变关系，图中以扭剪应变γZθ为横坐标，剪应力q(q=(α1-α3)/2)为纵坐标。在应力应变关系曲线图时可发现，在大主应力轴偏转角α=5°、20°、80°时，T1组试验的临界破坏扭剪应变值要大于T2组试验，而在大主应力轴偏转角α=35°、60°时，T2组试验的临界值则超过了T1组试验。

从扭剪应力-应变关系曲线看出，空心试样的临界破坏扭剪应变值在大主应力轴偏转角α<45°时，随着角度的增大而变大；而当大主应力轴偏转角大于45°时，则随着角度的增大而变小。在T1组试验中其临界破坏扭剪应变值在1%～2%(α<45°)、6%～12%(α>45°)之间；而在T2组试验中其临界破坏扭剪应变值在0.5%～1%(α<45°)、8%～22%(α>45°)之间。根据广义虎克定律与图4(a)、图4(b)曲线分析结果，在大主应力轴偏转角接近45°时候，切向应力会达到最大值，同时空心试样的扭剪应变应该也在45°左右达到最大值。图5中关系曲线表明试验结果基本与此相符合。图5与前图2、3、4相比较可见，当大主应力轴偏转角α<45°时，四个应变(轴向应变、切向应变、径向应变、扭剪应变)在数值上处于同一水平，而当大主应力轴偏转角接近并超过45°以后，扭剪应变明显高出其他三个应变近10倍。

2.2 主应力轴旋转下的剪切试验及分析

与定向剪切应力应变试验类似，主应力轴旋转下的剪切试验也以不同的b(b=0,b=0.5)值分为两大组，从而对比不同b值情况下土体经历主应力轴旋转后其应变性状的特征。其中b=O一组简称R1组试验试验(R11、R15)，b=0.5一组简称R2组试验试验(R21、R25)，试验方案详见表2。主应力轴旋转下的剪切试验的应力-应变图中仍以剪应力q(q=(α1-α3)/2)作为纵坐标，横坐标采用轴向、径向、切向及扭剪应变。

图6(a) b=0，0.5旋转剪切试验轴向应变应力图 图6(b) b=0，0.5旋转剪切试验径向应变应力图

图6(c) b=0，0.5旋转剪切试验切向应变应力图 图6(d) b=0，0.5旋转剪切试验扭剪应变应力图

在图6(a)、(b)、(c)、(d)中分别绘制了在主应力轴旋转下的剪切试验中4个应变分量(轴向应变，径向应变，切向应变，扭剪应变)的应力应变图。从图中曲线看出，图6(b)中不同中主应力参数下的曲线走势变化明显而其他三图变化较不显著，中主应力参数对径向应力-应变的影响较明显。

图中曲线显示，在定角度加载应力阶段，文中称为第一阶段(图中剪应力q从0kPa加压到20kPa)，空心试样应变变化大体上与T组试验中对应近似大主应力轴偏转角度试验所得曲线基本一致(R11—T13、R15—T23、R21—T11、R25—T21)。因此，第一阶段中的应力-应变曲线并无明显变化。而在主应力轴旋转下的剪切试验旋转大主应力轴偏转角并同时加压阶段，文中称为第二阶段(图中剪应力q从20kPa加压至破坏)，旋转空心试样大主应力轴到预定角度后增大剪应力直至破坏。图2(a)中T13与图6(a)中R11在达到临界破坏应力值后到试样完全破坏间曲线发展基本一致。因此，在试验R11中大主应力轴旋转角度后空心试样强度及临界破坏应变值未受到明显影响。对比其他各曲线，如图2(b)中T23与图6(a)中R15、图3(a)中T13与图6(b)中R11等，都有类似规律，即空心试样强度及临界破坏应变值并未受到大主应力轴旋转的影响。

从图6中各图曲线看出，R11与R21、R15与R25曲线走势基本相似。但是相同中主应力参数下，逆向旋转(35°～5°)时应变值与对应近似大主应力轴偏转角定向剪切应力应变试验应变值相近，而顺向旋转(5°～35°)时应变值明显小于对应近似大主应力轴偏转角定向剪切应力应变试验应变值。这表明了大主应力轴偏转方向对应变值有影响，与Symes等(1988)对饱和中砂试验的结论有相似性，即在进行主应力轴旋转时，角度递增则该应变值与相近大主应力轴方向的定向剪切试验应变值基本一致(R11与T13、R15与T23)；而如果角度递减则该应变值会更小些(R21与T11、R25与T21)。

3 结 语

(1) 从四个应变分量(轴向应变，切向应变，径向应变，扭剪应变)的试验结果可以认为，赣南软粘土土体的各向异性在应力-应变关系上有不同程度的反应。径向应变受到中主应力参数的影响较大，而中主应力参数与大主应力轴偏转角对扭剪应变有较大影响，尤其在主应力轴方向接近45°时，扭剪应变明显超出其他三个应变值。

(2) 大主应力偏转角度小于45°时，试样的应变值随着角度的增大而减小，试样在破坏时的临界应变值也随之减小，规律性较为显著；而在大主应力偏转角度大于45°之后，规律性较不明显；大主应力偏转角度逼近45°时，应变值趋于最大。

(3) 试样的强度及临界破坏应变值并未受到大主应力轴旋转的影响，主应力旋转并未对轴向应变，切向应变，径向应变，扭剪应变产生显著影响，中主应力参数对径向应变的影响仍然更显著。

(4) 大主应力轴的旋转会对试样产生应变累积，随着旋转方向角度递增产生的应变值要略高于旋转方向角度递减所产生的应变值。

[1]徐志伟．土体各向异性变形特性真三轴试验研究[D]．南京：河海大学，2003．

[2]HIGHT D W，GENS A，SYMES M J．The development of a new hollow cylinder apparatus for investigating the effects of principal stress rotation in soils[J]．Geotechnique，1983，33(4)：355-383．

[3]沈扬，周建，张金良，等．新型空心圆柱仪的研制与应用[J]．浙江大学学报：工学版，2007，4l(9)：1450-1456．

[4]Symes M J,Gens A,HIGHT D W.Undrained aniso-tropy and principal stress rotation in saturated sand[J].Geotechnique，1984,34(1)：11-27.

Research on Influence of Intermediate Principal Stress on Intact Soft Clay’s Strength and Deformation

WANG Yue-mei

( Jiangxi University of Science and Technology，Ganzhou 341000,China)

Soft clay in Gannan Prefecture has complex traits such as low shear strength,large void ratio,high compressibility and strong resistance of soil structure while the primary anisotropy and the secondary anisotropy of soft clay have the more complex affects about strain and deformation. The hollow cylinder apparatus(HAC) is aided to study the clay’s deformation according as its stress-strain relationship under conditions of changing parameter of intermediate principal stress and rotating principal stress. It’s revealed according to experimental data that the strain of intact soft clay is increased while rotating principal stress since the angle of first principal stress turns from 00 to 450 but decreased over 450. Affection from rotation of principal stress is not obvious while clay’s rotation accumulation arisen and the effect on radial strain is distinct from other strains due to the intact primary anisotropy as b=0.5.

parameter of intermediate principal stress；principal stress direction；anisotropy；principal stress rotation；intact soft clay

2015-10-09

江西省教育厅科学技术研究项目(GJJ14436)

王月梅(1977-)，女，江西吉安人，讲师，E-mail：yuemeiwang@126.com。

TU435

A

10.3969/j.issn.1671-234X.2015.04.004

1671-234X(2015)04-0014-07