几何画板融入中职数学教学的实践与思考

叶素慧

【摘 要】《中等职业学校数学教学大纲》要求教师更新观念、优化传统的教学方法，充分发挥计算机、互联网等现代信息技术的优势。在“重视现代信息技术与课程的整合，努力推进现代信息技术在职业教育教学中合理的应用”的道路上，信息技术与数学教学的整合已有了许多有益的尝试和研究。本文从几何画板在中职数学教学中的实例着手，剖析几何画板与中职数学教学的整合，使学生好学、会学、学会、学好。

【关键词】几何画板；中职数学； 整合

【中图分类号】G712 【文献标识码】B

【论文编号】1671-7384（2015）06-0078-03

几何画板融入中职数学教学的必要性

1.符合大纲理念和教学新要求的需要

《中等职业学校数学教学大纲》要求教师更新观念、优化传统的教学方法，充分发挥计算机、互联网等现代信息技术的优势。所以适当引入信息技术，加强其在教学中的地位，有利于学生理解数学概念、扩展思路，主动探索。

2.中职生现状的需要

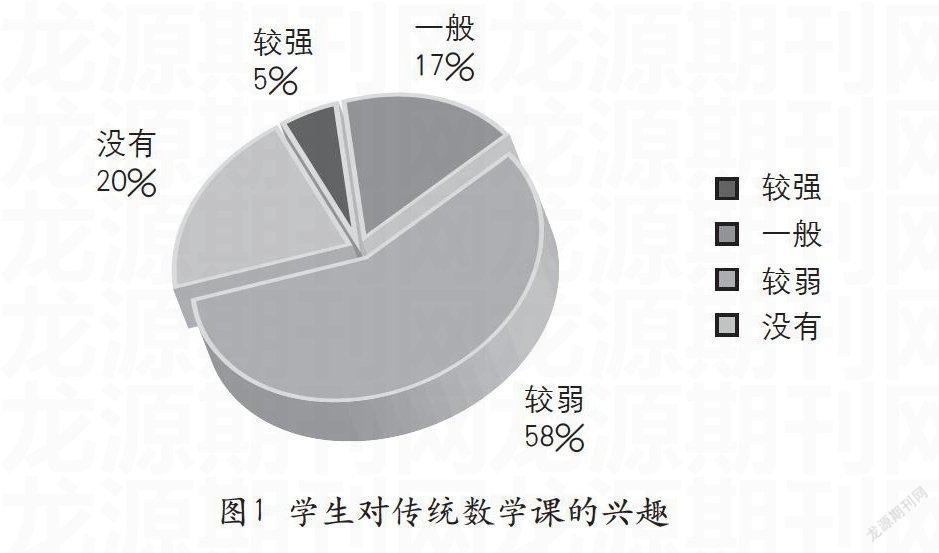
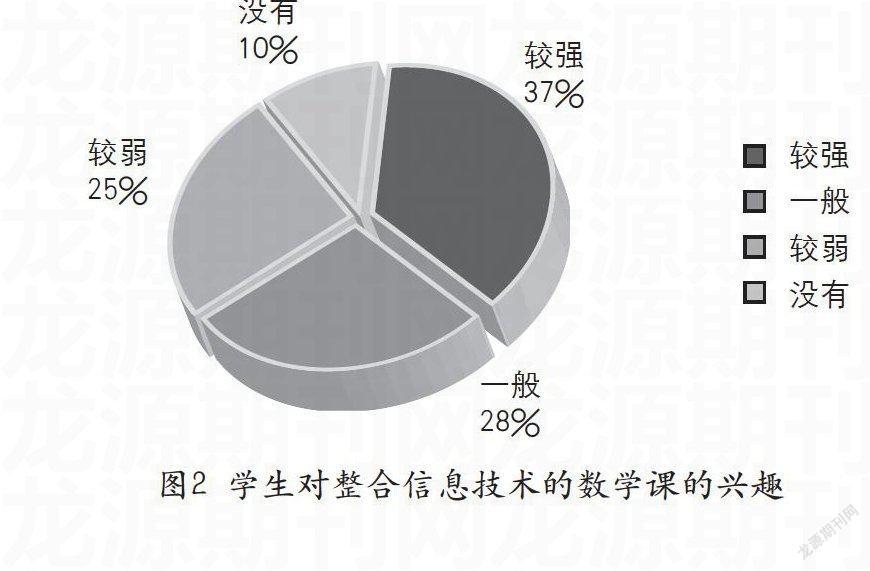
目前，中职数学教学面临许多困惑与挑战，部分学生起点低、差异大、极度厌学，尤其是数学学科，“老师几乎在课堂上唱独角戏”已成为中职数学课堂教学正常开展的瓶颈。如何激发学生学习兴趣，让学生参与课堂，是每位教师都在思考的问题。几何画板既能创设情境又能让学生主动参与，能有效地激发学生的学习兴趣，使抽象、枯燥的数学概念变得直观、形象，使学生从害怕、厌恶数学变成喜爱数学并乐意学习数学。学生通过主动发现、主动探索，不仅使其逻辑思维能力、空间想象能力和数学运算能力得到训练，而且还能有效培养其发散思维和直觉思维。笔者对本校的720名学生做了调查，结果显示，学生对数学的学习态度不乐观，而对与信息技术整合的数学课感兴趣 。

如图1所示，近80%的学生对学习数学的兴趣是一般和较弱，只有5%的学生有较强的兴趣，20%的学生没有兴趣。从这些数据上看出，数学教师的任务非常艰巨，改变课堂教学模式、提高学生学习兴趣是当务之急。

如图2所示，65%的学生对整合信息技术的数学课有兴趣，因为动画不仅吸引眼球，而且形象直观。几何画板融入数学课中，能有效地激发学生的学习兴趣。

几何画板有效融入中职数学教学的尝试

1.利用《几何画板》搭建突破概念教学难点的平台

【案例一】问题：平面内动点M满足到定点F与到定直线l的距离相等，动点M的轨迹是什么？

传统教学的不足：（1）若用尺规作图，涉及的一个距离是点到直线的距离，需要作垂线，找到垂足，再用直尺测量，不易操作。（2）找到的点个数有限，不能形成连续曲线，不易通过观察得到结果。

利用几何画板解决：（1）画出一条直线l和一个定点F，且点F不在直线l上。（2）在直线l上取点H，过点H作L的垂线MH。（3）作线段HF的中垂线，交MH于M。 （4）取M，并追踪点M的运动轨迹。（5）在直线l上拖动点H运动（或生成点H的动画，让其沿直线反复运动），则形成点M的运动轨迹——抛物线，如图3所示。

技术支持：（1）随着对某个几何对象的拖动，已构建的几何关系仍保持有效，几何图形变成动态的。同时，通过动画功能可以自动完成拖动几何图形的工作，从而生成美观、有趣且有启发性的图形，并且它们都是动态的，几何画板就是一个动态的几何学环境。（2）几何画板能由较简单的动画和运动通过定义、构造和变换，得到所需的复杂运动。使用便捷的轨迹跟踪功能，能清晰地了解目标的运动轨迹。椭圆和双曲线的形成可以通过实物模拟，但抛物线的实物模拟并不容易想到，且不易实现，利用几何画板的动态功能和追踪功能，解决了很多教师无法呈现抛物线形成过程的烦恼。

2.利用《几何画板》搭建验证问题和揭示问题本质的技术平台

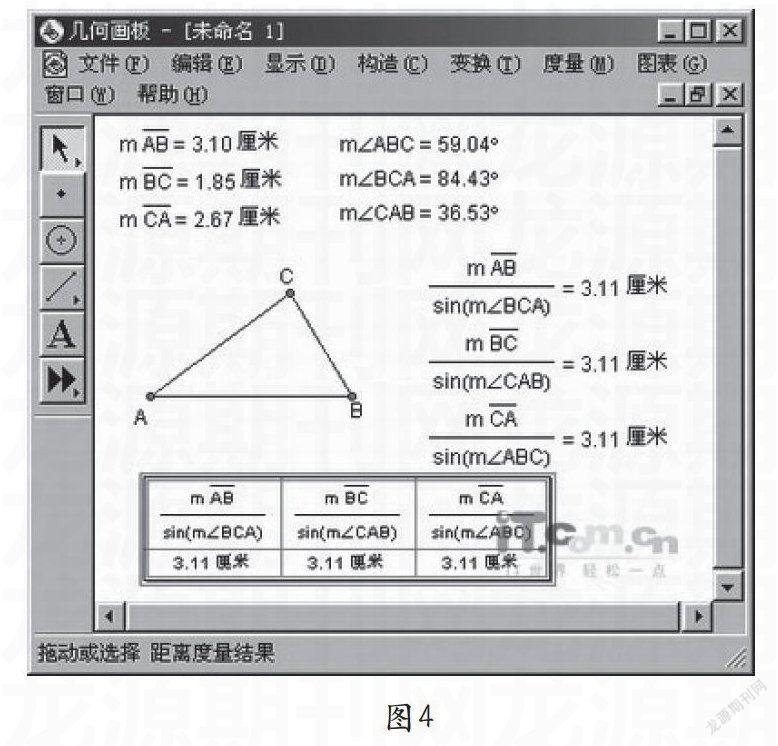
【案例二】：问题：在Rt△中，边与角之间是否存在等量关系：，是不是在一般三角形中也存在这样的边角关系？如何检验结论是否成立？

传统教学的不足：（1）通常教师让学生在直角三角形中证明这一性质，而在斜三角形中要证明对中职学生比较难，往往就草草地说明也适用。（2）如果通过实验指导学生画出任意一个三角形，需要用直尺和量角器对三条边和三个内角进行测量，测量数据有一定误差；角度一般都不是特殊角，需要查表或用计算器计算其正弦值，再代入运算，运算结果也会存在误差。

如图4所示，利用几何画板解决： （1）画出三个不共线的点，并用线段把它们连接起来，形成三角形ABC。（2）度量三个内角的大小及三条边的长度。（3）计算三个比值：，，。（4）拖动顶点A，可以任意改变三角形的形状，从而引起三个内角及三条边的数值变化，可以观察到三组比值虽然在变，但总保持相等。

技术支持：（1）几何画板最大的特色就是“动态性”，即可以用鼠标拖动图形上的任一元素（如点、线、圆等），而事先给定的所有几何关系（即图形的基本性质）都保持不变。在上述三角形中，我们拉动其中的一个点，同时图形的形状就会发生变化，但仍然保持是三角形。（2）几何画板具有强大的计算功能，不仅能完成定值的计算，还能进行变量的计算。教师选择用几何画板完成检验过程，不仅省去了烦琐的度量计算，还让学生直观感受到结论的正确性。

3.运用几何画板为揭示变化规律创建平台

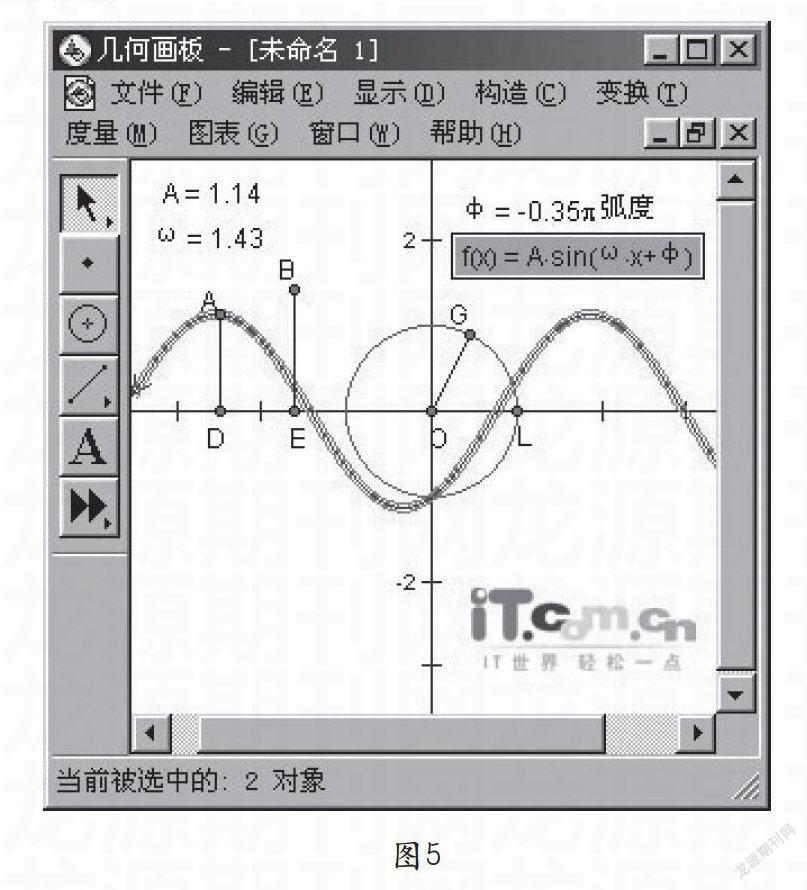
【案例三】：探索正弦型函数y=sin（wx+j）的函数图象性质。

传统教学的不足：一般课程中都是以三个特殊值来说明，几个有限的取值描述后就加以归纳，其不全面的归纳对学生的认知影响是显而易见的。

利用几何画板解决：拖动课件中的A，w，j，就可以在其下面看到相应的值（如图5），同时可以看到函数图象的连续变化，通过直观生动的图象变换，学生很容易就能完成y=Asin（wx+j）的函数性质的学习。

技术支持：（1）随着对某个几何对象的拖动，几何图形变成动态的。同时，通过动画功能可以自动完成拖动几何图形的工作，从而生成美观的或有趣的或很有启发性的图形，并且它们都是动态的。（2）几何画板不仅省去了画图的时间，让学生直观感受图形变化规律，还使教学过程形象生动，大大提高了课堂效率，激发了学生学习的兴趣。

几何画板融入中职数学教学的思考

1.运用几何画板要科学合理

新技术是一把双刃剑，使用不当自然会有一定的副作用。一线教师使用几何画板辅助数学教学时应通盘考虑几何画板的性能特征、学生学习心理和思维规律、具体授课内容等，遵循实事求是、主体参与的原则。几何画板辅助教学和传统教法各有利弊，不是“非此即彼、完全取代”的关系，而应有机结合，互为补充，该用传统教法的课，不必作茧自缚而舍近求远。另外，数学教师不应坐失良机，更不应该排斥看似简单的几何画板或盲目崇拜新技术。

2.运用几何画板要适时适量

符合学生的认知规律运用几何画板教学，可减少教师的讲解，且助于教师的讲解。教师的讲解要与演示紧密结合，不论采用何种方式讲解，都应抓住教学内容的重点、难点、要点、疑点，抓住教学内容的内在联系进行讲解。在使用课件之前，应告诉学生观察什么，使学生有明确的目标，以便集中精力先看什么后看什么。怎样演示（如先拖动还是先动画），是否重复演示都要十分讲究，要缜密考虑，做到胸有成竹。

3.运用几何画板实现数学课堂组织形式的开放

如果有条件的话，可以把课堂从多媒体教室转移到微机教室，让每位学生都亲自动手实验，改变任何一个参数，通过观察、比较、分析得出自己的结论，这样的效果更理想。学生在互相讨论、教师点拨指导等过程中，得出自己的结论，逐渐形成自己的知识体系，达到知识的重建，这有利于学生从实践中发现问题、解决问题，主动地学习数学，提高数学思维能力。通过此方法，教师可以把学生从被动的学习中解脱出来，主动地思考数学问题，真正提高学生的学习能力。这种开放性的教学可以培养和促进学生的好奇心和求知欲，激发学生探索的热情。

总之，应用几何画板进行中职数学教学，能使中职学生更有实感地去把握数学，而不是把数学作为单纯的知识去理解，既能激发中职学生的学习热情、培养中职学生学习数学的兴趣，又能大大提高课堂效率。

（作者单位：浙江台州市椒江中等职业技术学校）