基于双直方图均衡化的彩色图像增强

田小平, 乔 东, 吴成茂

(西安邮电大学 电子工程学院， 陕西 西安 710121)

基于双直方图均衡化的彩色图像增强

田小平, 乔 东, 吴成茂

(西安邮电大学 电子工程学院， 陕西 西安 710121)

在彩色图像增强中，为了保留更多图像细节，提出一种基于HSV色彩空间的彩色图像增强算法。通过引入一种新的累积分布函数，改进双直方图均衡化算法，用以对色彩空间转换分离后的亮度分量实施均衡化，并保持原图像色调和饱和度不变，再将经过处理后的HSV图像还原回RGB图像得到最终结果。以边缘检测为客观标准，肉眼感知为主观标准，分析该方法的有效性，并与现有的方法相比得知，所给方法可在实现图像增强的同时保持图像的细节信息。

图像增强；双直方图均衡；RGB图像；HSV图像

图像增强通过对图像在空域或频域进行特定算法处理,以改善图像的视觉效果或者增强图像的某些特定信息，来满足人眼视觉或者机器视觉的要求[1]。彩色图像包含比灰度图像更多的信息层次[2]，在视觉感官和后续图像分析方面，都优于灰度图像，应用十分广泛，但因在不同场景获取的彩色图像整体光照不均或颜色减少，所以有必要对其进行增强。

彩色图像增强的目的是为了突出图像细节，增强有用信息，改善图像视觉效果，并在尽可能保持图像彩色信息的同时，使得图像更加生动醒目，易于辨识和处理[3]。借鉴直方图均衡化在灰度图像中的应用[4-5]，并考虑到彩色图像的多分量属性，可以对RGB彩色图像每个分量分别进行直方图均衡化处理[6]，但此做法很可能产生不正确彩色，在增强图像信息的同时存在失真[7]。

本文拟提出一种色彩保持双直方图均衡(Color Preserving Based on Bi-Histogram Equalization，CPBBHE)算法，即选择HSV(Hue, Saturation, Value)彩色空间模型，采用彩色空间转换[8]，仅对亮度分量进行双直方图均衡化处理[9-10]，而不改变色度和饱和度，以求在保持色彩不变的情形下，增强图像的某些特殊信息。

1 彩色模型转换

彩色模型的作用是在某种标准下，以通常可被接受的方式，方便地对彩色加以说明，即利用坐标系和子空间的思想，将每种颜色表示为一些单点。

1.1 RGB色彩模型

自然界中绝大部分可见光谱可以用红、绿和蓝三色光，按不同比例和强度的混合来表示，这就是RGB色彩模型。用字母R、G、B分别代表某光谱的三基色分量，为其各分配一个0～255范围内的强度值，按不同比例混合就能得到相应的颜色。例如:纯红色R值为255，G和B值为0；白色的R、G、B都为255；黑色的R、G、B都为0。这样下来可以得到16 777 216种颜色。

1.2 HSV色彩模型

HSV色彩空间的模型对应于圆柱坐标系中的一个圆锥形子集(图1)。圆锥的顶面对应于V=1。它包含RGB模型中的R=1，G=1，B=1三面，所代表的颜色较亮。色彩H由绕V轴的旋转角给定。红色对应于角度0°，绿色对应于角度120°，蓝色对应于角度240°。在HSV颜色模型中，每一种颜色和它的补色相差180°。饱和度S取值从0到1。HSV色彩空间可以从图像中包含的彩色信息(色调、饱和度)中消去亮度分量的影响，是开发基于彩色描述图像处理方法的理想工具[11]。

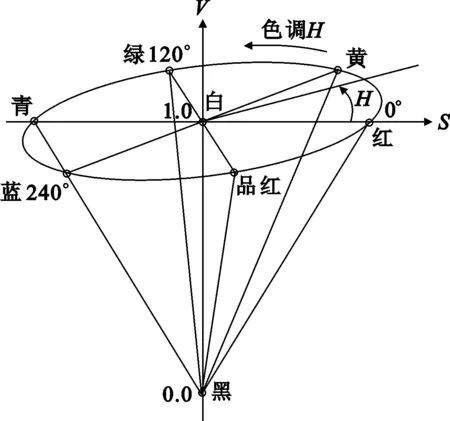
图1 HSV彩色空间模型

1.3 RGB和HSV色彩空间相互转换公式

1.3.1 RGB模型转换到HSV模型

给定一幅RGB彩色格式的图像，对[0,1]范围内的R、G、B值，其对应的HSV模型中的V、S、H分量的计算公式分别为[12]

1.3.2 HSV模型转换到RGB模型

HSV模型下对应于RGB模型中R、G、B分量的计算公式为[12]

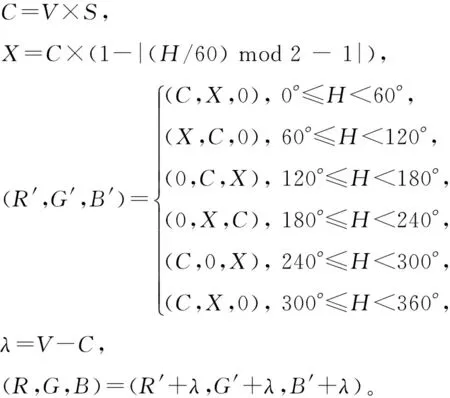
2 双直方图分割与均衡

直方图均衡化就是把给定图像的灰度直方图分布,改造成近似均匀的直方图分布, 使得输出图像像素灰度的概率密度均匀分布。直方图均衡化算法主要用于灰度图像处理, 因此将其应用于彩色图像处理时，仅作用于彩色图像的某一分量。在进行直方图分割后, CPBBHE算法根据两个子区间内的直方图所进行的均衡化处理，均只针对分量V。

2.1 阈值分割

用X表示输入图像亮度分量的二维数组并且将其数值映射到[0,255]区间上,即

其中Xi,j代表像素点(i,j)处的灰度值。以L代表亮度灰度级，并预先设定L=256，记m为分割阈值。

对于阈值的选取采用迭代法[13]，选择一个近似阈值m，将图像各像素点的灰度值分割成R1和R2两区域，计算其均值μ1和μ2。选择新的分割阈值

重复上述步骤直到μ1和μ2不再变化为止。用m作为分割点，将图像直方图H分为灰度值小于m的HL和灰度值大于m的HU两个子直方图,即

H=HL∪HU。

2.2 构造累积分布函数

分割后，分别计算两个子直方图的每级灰度的概率密度[14]

其中k=0,1,…,L-1,而HL(k)和HU(k)分别表示在两个子直方图中灰度级k出现的次数。p(k)与输入图像的直方图有关，代表亮度k的像素概率。基于概率密度函数，定义累积分布函数[2]

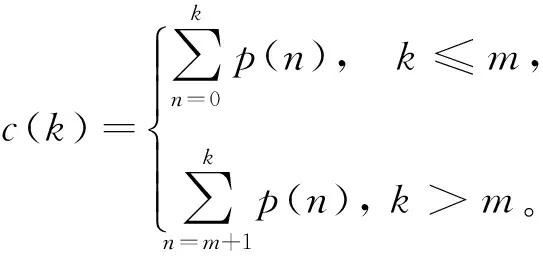
用μL和μU分别代表HL和Hu的中位数，且有

根据子直方图的中位数创建S型函数[15]

如图2所示，s(k)函数是一个平滑的S形函数。当取r≥1时,s(k)在区间[-5,5]上的值域为[0,1]，并且在区间外s(k)的取值基本接近0或者1，这也正好符合累积分布函数的分布规律。由s(k)函数曲线走势可见，变换曲线的左半部分可以使变换后的灰度值更小，右半部分可以使变换后的灰度值更大，这样全图的对比度就会增加，而且如果左下部的曲线越低，右上部曲线越高，对比度增强越明显[16]。不妨取r=1.5。

图2 s(k)曲线分布

为了得到一个值域在[-5,5]区间上的函数，选定函数

其中

若仅考虑β=1时的情形，就会失去一般性[15]，故可考虑通过分析实验结果，选取具有自适应性的参数β=mr/255，其中m代表分割阈值，r是关于函数s(k)的平滑度参数。

2.3 图像映射

通过对累积分布函数的替换进行图像的映射，根据不同灰度级计算出对应映射灰度,即取

其中L0和Lf分别表示输出图像灰度级动态范围的上下限。在CPBBHE算法中，取

L0=0，

Lf=L-1。

直方图均衡化处理难免会对一些灰度级进行合并，使图像的某些细节消失。映射完后还需适当的灰度拉伸[17]，以扩大图像处理后灰度级动态范围，提高视觉效果。具体的变换函数为

其中

通过以上计算，即可得出关于灰度级k的映射数组T(k)。增强后的图像Y可表示为

Y=T(X)。

3 实验仿真

图3是低照度图像window在5种图像增强算法下的增强效果。可以看出直方图均衡算法(Histogram Equalization,HE)处理后图像的亮度有明显提高，但是对于亮度较强部分过度增强；而保持亮度的直方图均衡(Brightness preserving Bi-Histogram Equalization ,BBHE)使得图像亮度两极分化，导致很严重的失真；相对于HE算法和BBHE算法，最小均方误差双直方图均衡(Minimum Mean Brightness Error Bi-Histogram Equalization,MMBEBHE)改进很多，但是增强的效果不明显；迭代阈值的子块部分重叠双直方图均衡(Iteration threshold based on Partially Overlapped Sub-blocks Bi-Histogram Equalization,IPOSBHE)[13]可让图像的细节逐渐突显出来，但该方法对低照度图像的增强依然不够明显。图3(f)是采用CPBBHE的算法得到的，不同程度上克服了前面几种方法的缺点。

图3 window图像实验结果

采用Canny边缘算子[18]得到的检测结果如图4所示，不难看出算法HE、BBHE、MMBEBHE和IPOSBHE对灰度级合并较为明显，而CPBBHE算法则保留了原始图像的细节信息。

图4 Canny边缘算子检测结果

再次选择亮度图像重复上述实验，结果如图5和图6所示。

图5 Couple图像实验结果

图6 Room图像实验结果

观察图5与图6，从中所得结论与从图3所得结论基本一致。分别给出相应算法Canny边缘检测结果，如图7和图8所示。

从上述实验结果来看，HE算法处理后的图像亮度有明显提高，但兼并了很多细节信息，而算法BBHE、 MMBEHE及IPOSBHE对于低照度图像的增强效果并不明显，对于高亮度图像又产生了噪声干扰。相比而言，CPBBHE算法能很好地适应不同图像，在增强图像的同时保留图像细节信息，有利于目标检测和特征提取等图像后续处理。

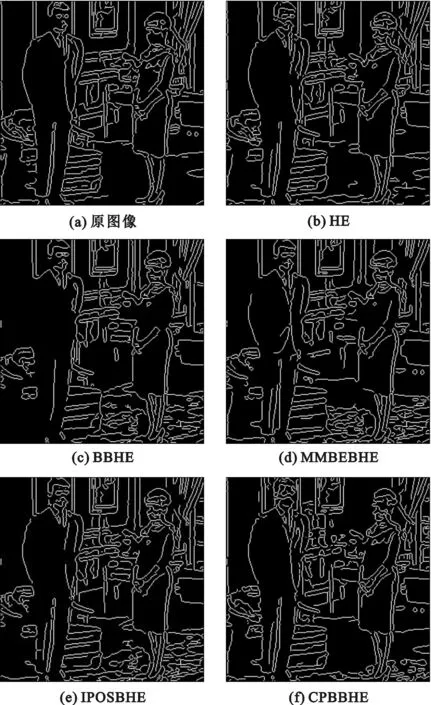
图7 Couple图像边缘算子检测结果

图8 Room图像边缘算子检测结果

4 结语

利用基于双直方图均衡化的彩色图像增强方法，可将RGB色彩空间转换到HSV色彩空间，通过对V分量进行双直方图均衡处理，可以达到增强且保留图像细节信息的目的。与其他4种直方图处理方法不同，CPBBHE算法引入了一种新的S形函数，作为累积分布函数。实验选取低照度图像和亮度图像，通过Matlab仿真，并采用Canny算子进行边缘检测，可知图像细节信息并未丢失。

[1] 李艳梅. 图像增强的相关技术及应用研究[D]. 成都：电子科技大学, 2013:15-28.

[2] Koschan A, Abidi M. 彩色数字图像处理[M].章毓晋,译.北京：清华大学出版社,2010:6-14.

[3] Xie Xiaomin, Wang Changming, Zhang Aijun. Color Image Enhancement Methods Based on Matlab[J]. Applied Mechanics and Materials, 2013, 300(1): 1664-1668.

[4] 武英. 基于双直方图均衡的自适应图像增强算法[J]. 计算机工程, 2011, 37(4):244-245.

[5] Sengee N, Sengee A, Choi H K. Image contrast enhancement using bi-histogram equalization with neighborhood metrics[J].IEEE Transactions on Consumer Electronics,2010, 56(4): 2727-2734.

[6] 胡琼,汪荣贵,胡韦伟,等.基于直方图分割的彩色图像增强算法[J].中国图象图形学报,2009,14(9): 1776-1781.

[7] 任洁.彩色图像增强算法的研究与实现[D].武汉：武汉理工大学,2013:12-15.

[8] 高静波,吴成茂,田小平.基于清晰度的彩色图像量子增强算法[J].西安邮电学院学报,2011,16(2):4-8.

[9] Kim Y T. Contrast enhancement using brightness preserving bi-histogram equalization[J]. IEEE Transactions on Consumer Electronics,1997,43(1):1-8.

[10] Chen S D, Ramli A R. Minimum mean brightness error bi-histogram equalization in contrast enhancement [J]. IEEE Transactions on Consumer Electronics, 2003, 49 (4): 1310-1319.

[11] 王旭峰,董新民,孔星炜,等.一种基于HSV色彩空间的加油锥套特证提取方法[J].计算机应用与软件,2014,31(6):192-194.

[12] 蔡式东,杨芳.一种基于HSV空间和粗糙集的彩色图像分割方法[J].光电子技术,2011,31(1):5-9.

[13] 孙水发,李乐鹏,董方敏,等.基于迭代阈值的子块部分重叠双直方图均衡算法[J].广西师范大学学报:自然科学版, 2013,31(3):119-126.

[14] Kim Y T. Contrast enhancement using brightness preserving bi-histogram equalization[J]. IEEE Transactions on Consumer Electronics,1997,43(1):1-8.

[15] Arriaga-Garcia E F, Sanchez-Yanez R E, Garcia-Hernandez M G. Image enhancement using Bi-Histogram Equalization with adaptive sigmoid functions[C]//2014 International Conference on Electronics, Communications and Computers. NY, USA :IEEE, 2014: 28-34.

[16] 田小平,李晓敏.基于小波变换的遥感图像增强方法[J].西安邮电大学学报,2014,19(2),38-42.

[17] Arici T, Dikbas S, Altunbasak Y. A histogram modification framework and its application for image contrast enhancement[J]. IEEE Transactions on Image Processing, 2009, 18(9): 1921-1935.

[18] 余洪山,王耀南.一种改进型 Canny 边缘检测算法[J]. 计算机工程与应用, 2005, 40(20): 27-29.

[责任编辑:瑞金]

Color image enhancement based on bi-histogram equalization

TIAN Xiaoping, QIAO Dong, WU Chengmao

(School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

The color image enhancement algorithms have some disadvantages in terms of detail preservation. To solve this problems, a color image enhancement method based on HSV color space is proposed. an new cumulative distribution function is introduced to improve bi-histogram equalization algorithm, thus it can is used to equalize the brightness component while the original image hue and saturation remains unchanged. Then the image is converted from HSV color space to RGB color space, and the enhanced color image is obtained. With edge detection as objective and naked perceived as subjective criteria to analyze the effectiveness of the method, and compared that with the existing method, the new method can enhance color image and also ensures the details of the image to be better kept.

image enhancement, bi-histogram equalization, RGB image, HSV image

2014-07-31

国家自然科学基金资助项目(90607008)；陕西省自然科学基金资助项目(2014JM8331，2014JQ5183，2014JM8307)；陕西省教育厅科学研究计划资助项目(2013JK1129)

田小平(1963-)，男，教授，从事信号与信息处理技术研究。E-mail: xptian@xupt.edu.cn 乔东(1988-)，男，硕士研究生，研究方向为视频图像处理。E-mail:qiaodong1208@126.com

10.13682/j.issn.2095-6533.2015.02.012

TP751.1

A

2095-6533(2015)02-0058-06