浮点超越函数设计与实现

杜慧敏, 沙 亮， 张彦芳， 牛志璐

(西安邮电大学 电子工程学院， 陕西 西安 710121)

浮点超越函数设计与实现

杜慧敏, 沙 亮， 张彦芳， 牛志璐

(西安邮电大学 电子工程学院， 陕西 西安 710121)

针对图形处理器中浮点超越函数，设计一种单精度浮点超越函数专用计算电路。该电路基于CORDIC参数扩展算法，通过映射和补偿处理扩展计算范围，修改初值设置方式节省部分计算开销，依据Matlab模型仿真设计FPGA电路实现。实验结果表明，在Xilinx Virtex6器件上电路的最大工作频率可达182.916MHz，以39至67时钟周期完成一次计算，计算周期减少。

CORDIC；参数扩展；浮点超越函数；图形处理器

超越函数计算是通信信号及处理器应用中常用的数学计算。在通信信号处理中，三角类超越函数被用于信号调制解调[1]；而在处理器中，则支持更高精度的浮点超越函数计算是科学计算和复杂算法的重要部分。在图形处理器统一着色应用中[2]，需要进行多次大量的浮点正余弦、指数、对数和平方根计算[3]。

超越函数主要的实现方法有坐标旋转数字计算算法(Coordinate Rotation Digital Computer，CORDIC)[4]、查找表法[5]、级数拟合、函数逼近等[6]。通信系统中混频所用三角超越函数通常采用CORDIC算法和查找表方法实现[7]，但仅用于位宽较小的定点格式。在科学计算和处理器应用中，浮点格式数据要求更高精度算法支持，通用处理器借助CORDIC、函数逼近等较高精度算法，由软件方式实现计算[8]，但其指令调度耗时较长。而更多处理器采用专用数学协处理器[9]计算超越函数，虽较软件方式更快，但已知的专用电路[10]计算种类和范围有限，仍消耗较多时钟周期。

本文基于CORDIC参数扩展算法[11]，设计一种单精度浮点超越函数的专用计算电路，用于计算正余弦、反正切、双曲正余弦、指数、反双曲正切、对数、平方根9种函数。在CORDIC核心迭代计算前后分别引入映射和补偿处理，扩展函数计算范围，并对平方根和旋转模式下若干函数初值设定方式进行改进。设计采用Matlab仿真，搭建FPGA电路，在SystemVerilog平台和微控处理器平台上验证。

1 CORDIC参数扩展算法

CORDIC基本算法中参数扩展算法[11]提供了圆坐标和双曲坐标、旋转模式和向量模式4种搭配的计算9种超越函数方法。

算法中约定浮点数FLP表示为S×M×2E，其中S为符号，E为阶码，M为尾码。圆坐标旋转模式可计算正弦和余弦函数，X、Y通路设定初始值

X0=SX0×MX0×2EX0=0.607 252 93，Y0=SY0×MY0×2EY0=0，

待计算角从Z0输入，

Z0=SZ0×MZ0×2EZ0。

扩展算法划分为对阶、映射、迭代、补偿、规格化5步流程。

(1)对阶：

Eref=max(EX0,EY0)，

尾码移位

MX1=MX0×2(EX0-Eref)，MY1=MY0×2(EY0-Eref)，

输出对阶码Eref和尾码MX1、MY1。

(2)映射：

MZ1=Q×(π/2)+R，

MZ1乘2/π取整可提取Q值，取余后乘π/2提取R值，令MZ2=R。根据表1关系将MX1、MY1映射至基本收敛域[0,π/2]内，输出MX2、MY2、MZ2。

表1 Q模4值映射关系

(3)迭代：MX2、MY2、MZ2进入CORDIC迭代单元经N次迭代计算出MX3、MY3。

(4)补偿：正弦和余弦函数无需补偿。

(5)规格化：对MX3、MY3及相应符号和阶码规格化处理，输出计算结果。

圆坐标向量模式和双曲坐标旋转、向量模式有以下不同细节。

圆坐标向量模式可计算反正切函数，设定初值

X0=1， Z0=0，

映射和补偿只需直传。

双曲坐标旋转模式可计算双曲正余弦和指数函数[11]，设定初值

X0=1.207 497 06， Z0=0，

通过

MZ1=Q×ln2+R

提取ln2的整倍数Q和余数R，依据

MX2=(MX1+MY1)+2-2Q(MX1-MY1)，MY2=(MX1+MY1) -2-2Q(MX1-MY1)，

将待计算角度映射至基本收敛域[0,ln2]内，以及相应的补偿变换。

双曲坐标向量模式可计算反双曲正切、对数和平方根函数，根据比值MY1/MX1位于[0,0.5]或(0.5,1]直传或映射，映射公式[11]

MX2=(MX1+MY1)+22Enew(MX1-MY1)，MY2=(MX1+MY1) -22Enew(MX1-MY1)，

其中Enew为(MY1-MX1)的前导零数，迭代后做Enew相应的补偿处理。

2 浮点超越函数设计

设计包含正余弦、反正切、双曲正余弦、指数、反双曲正切、对数、平方根9种函数，通过MATLAB仿真验证改进算法的正确性，然后编写代码设计电路，并在FPGA上实现。以正余弦函数电路为例论述，其余相似。

2.1 算法的改进

对平方根和旋转模式下正余弦、双曲正余弦和指数等函数的初值设定方式进行改进。

(1)平方根计算是由双曲坐标向量模式迭代X通路结果

(1)

算得，其中Kn为伸缩因子。传统方法设置初值

X0=Din+1/4, Y0=Din-1/4，

其中Din为平方根待计算值,代入式(1)可得

Xn= Kn((Din+1/4)1/2-

如令初值

X0=Din+1， Y0=Din-1，

可得

Xn=Kn((Din+1)1/2-

(Din-1)1/2)=Kn(4Din)1/2。

该设置可使MY1/MX1值全部落入[0,0.5]，映射处理可以直传，补偿将多出的系数2消去即可，回避了落入(0.5,1]区间映射所必须的加减、左移和前导零计算。对数计算方法也做了同样改进。

(2)旋转模式下正余弦、双曲正余弦和指数5个函数X、Y通路初值为常量，可将对阶值预先计算并存储，将预计算值直接送给映射处理，这样优化可省去浮点数对阶计算的耗时和面积。

2.2 MATLAB仿真

对改进算法进行MATLAB模型仿真，结果表明模型能够正确计算。图1为正余弦函数算法模型与函数波形对比。

图1 正余弦函数算法与函数波形精度对比

图1中在[0,2π)间均匀取样30个数据点，圆圈o和方框□分别为MATLAB内建正弦和余弦函数计算结果，+为算法模型计算结果，可以观察到+全部精准落在o和□内部中心，表明两者计算结果一致。

其余函数也进行了全覆盖仿真测试，结果表明在表2范围内计算结果绝对误差均小于10-7，满足IEEE-754单精度浮点数精度(注：此范围内要求为规格化浮点数，包含0，3.4028×1038为单精度浮点数最大表示值)。

表2 扩展前后函数计算范围表(rad)

2.3 FPGA实现

依据算法仿真模型设计电路结构，在FPGA上搭建和验证电路计算。

2.3.1 总体结构

该结构将数据通路划分为5级流水处理，分别对应算法中5步流程，如图2所示。

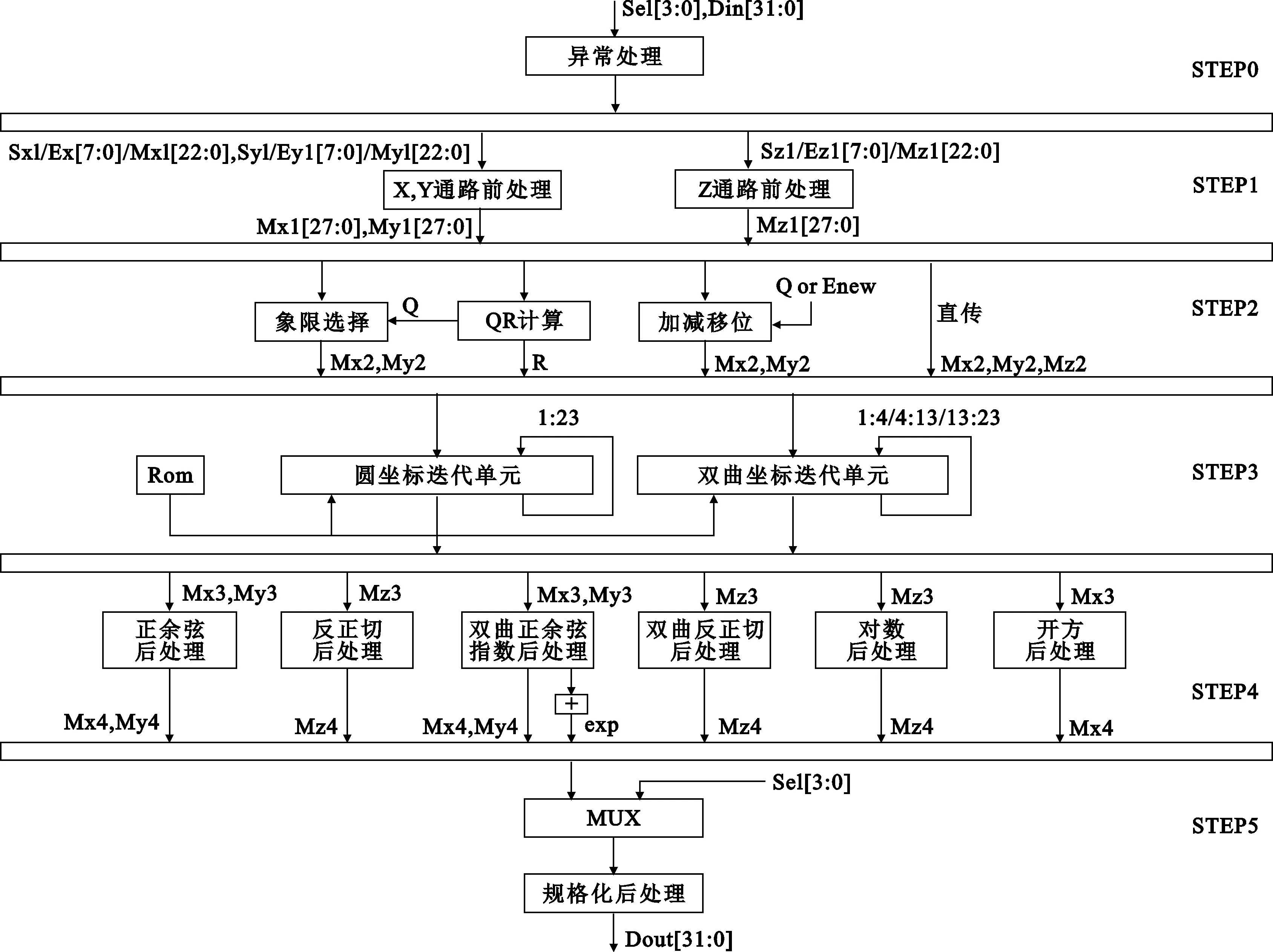
图2 浮点超越函数总体结构数据通路

9种函数依照坐标、模式、处理相似性和电路重用性划分6个函数子模块实现，顶层由状态机调度计算与跳转。

2.3.2 函数子模块设计

正余弦子模块结构如图3所示。

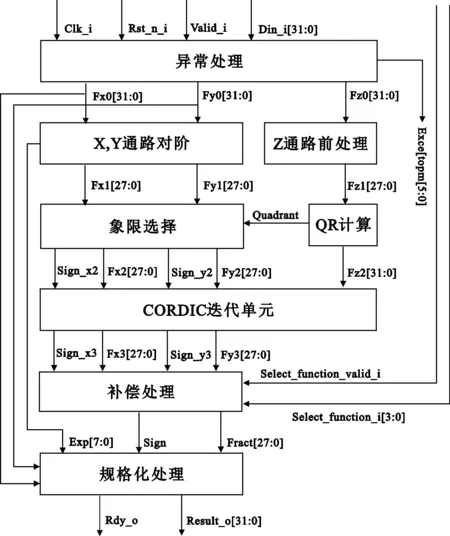
图3 正余弦函数子模块结构

(1) 5级流水前先由异常处理模块判断输入值是否为合法格式的单精度浮点数，以及是否位于函数合法计算范围。X、Y通路设定常初值，对阶模块计算阶差并将阶码较小的尾码移位，提取对阶码和尾码。Z通路前处理模块将浮点输入待计算值转换为适合迭代单元的28位定点格式。

(2) QR计算模块由比较电路计算得映射所需的Q及R值，象限映射模块根据Q值将X、Y通路尾码映射至基本象限。

(3) 三通路尾码和符号同时具备进入迭代单元，经过23次迭代输出X、Y路尾码和符号，结构如图4所示,其中Xi、Yi和Zi为第i次迭代值。

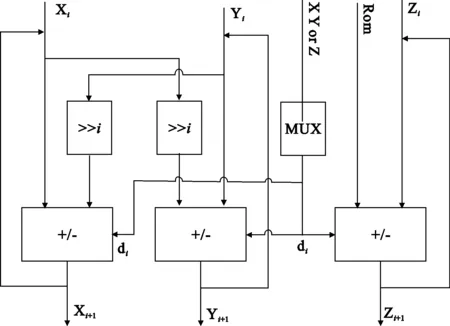
图4 CORDIC迭代单元结构

迭代单元包含3个数据通路的迭代加减，X、Y路移位后交叉加减，Z路与rom里存储的迭代序列加减，旋转模式时方向因子di由前次迭代Z值算得，向量模式时di由X、Y值算得。圆坐标时迭代23次，双曲坐标时在第4、13次重复，共迭代25次。

(4)正余弦补偿处理模块只需直传。

(5)规格化模块将前级传送的尾码和符号以及之前提取的对阶码恢复处理为规格化浮点数，输出结果。

其他函数子模块在此结构上增删若干模块。待计算值输入通路和初值设定不同，映射和补偿模块相应调整。

3 实验验证

3.1 System Verilog平台验证

先在Modelsim中完成一定量定向测试，包括特殊值、临界和边界值，然后在SystemVerilog平台上验证。

如图5，SV平台发生器产生随机种子送给参考模型和驱动器，驱动器根据待测电路时序驱动电路求值计算，计算结果传给监视器，同时，参考模型的C程序将正确参考值写入记分板，由监视器比对两者结果。

图5 SystemVerilog验证平台

设定10-7精度的随机值测试显示，电路计算结果与函数的数学理论值相同，表明计算正确。

3.2 微控处理器平台验证

该电路作为超越函数计算单元加入微控处理器平台的浮点单元，增加超越函数指令驱动电路计算进行验证。结构如图6所示。

该计算单元在Xilinx Virtex6器件最大工作频率达到182.916MHz，选取一定量数据对电路进行计算测试，结果如表3显示，平均绝对误差最小值达10-9，最大值达10-7。

图6 超越函数单元在微控处理器中结构

表3 9种函数平均绝对误差

双精度混合模式浮点CORDIC协处理器[10]用69周期完成一次计算，而该设计的单精度浮点超越函数电路在反正切计算中最快只需39个时钟周期，其余需要41到67不等的时钟周期完成一次计算，如表4所示。

表4 9种函数时钟周期开销

SystemVerilog与微控处理器两项验证表明该电路计算正确，误差小于10-7，符合单精度浮点标准，计算周期有一定减少。

4 结束语

基于CORDIC参数扩展算法，通过引入映射和补偿处理，扩展了函数计算范围，改进了初值设定方式，优化了非必要的计算开销，依据算法的Matlab仿真实现了FPGA电路，并在SystemVerilog平台与微控处理器平台上进行验证。该浮点超越函数专用计算电路，可以更短的时钟周期完成计算，满足图形应用及处理器中超越函数计算对速度和精度的需求。

[1] 何宾. FPGA 数字信号处理实现原理及方法[M]. 北京：清华大学出版社, 2010:107-113.

[2] 焦继业.低功耗高性能移动图形顶点处理器设计关键技术研究[D].西安：西安电子科技大学，2013:75-82.

[3] 杜慧敏,李萌.面向顶点染色算法的专用指令集优化处理器[J].西安邮电大学学报，2014,19(2):60-66.

[4] Volder J E. The CORDIC trigonometric computing technique[J]. Electronic Computers, IRE Transactions on, 1959 (3): 330-334.

[5] 李坤贺,岳曾敬.基于查找表和CORDIC算法的混合型NCO设计[J].兵器自动化，2014,33(3):43-46.

[6] 杜慧敏,马超.一种快速浮点乘法单元的设计与实现[J].西安邮电大学学报，2013,18(3):62-66.

[7] 王玉良,李宏生,夏敦柱.基于CORDIC算法的NCO在FPGA中的实现[J].计算机与数字工程，2009,12(3):21-23.

[8] 陆一倩.在MDS-287中用8086和8087计算超越函数的精度和执行速度的比较[J].微计算机应用，1985,3(5):51-56.

[9] 梁政,杨银堂,沈绪榜.LSC87嵌入式协处理器中超越函数的实现方法[J].西安电子科技大学学报，2001,28(2):258-260.

[10] Zhou Jie, Dou Yong, Lei Yuanwu, et al. Double precision hybrid-mode floating-point fpga cordic co-processor[C]//10th IEEE International Conference on High Performance Computing and Communications. Zhangjiajie: IEEE, 2008: 182-189.

[11] Hahn H, Timmermann D, Hosticka B J, et al. A unified and division-free CORDIC argument reduction method with unlimited convergence domain including inverse hyperbolic functions[J]. Computers, IEEE Transactions on, 1994, 43(11): 1339-1344.

[责任编辑:祝剑]

Design and implementation of floating-point elementary functions

DU Huimin， SHA Liang， ZHANG Yanfang， NIU Zhilu

(School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

To calculate Floating-point elementary functions in GPU, a single-precision Floating-point elementary functions compute circuit of 9 functions is designed in this paper. This circuit is based on CORDIC Argument Reduction Algorithm, to expand the region by adding mapping and compensate processing, and to reduce part of circuit by improving initial value setting. According to simulation on Matlab, a FPGA circuit is implemented and verified. Experimental results show that it can work at maximum frequency of 182.916MHz on Xilinx Virtex6, one time in 39 to 67 clock cycle，and therefore can reduce the calculation cycle.

CORDIC, argument reduction, floating-point elementary functions, GPU

2014-09-23

国家自然科学基金重大项目(61136002)

杜慧敏(1966-),女，博士，教授，从事集成电路设计、计算机体系结构及图形学方向研究。E-mail:fv@xupt.edu.cn 沙亮(1983-),男，硕士研究生，研究方向为专用集成电路设计与系统集成。E-mail:vipshl@sina.com

10.13682/j.issn.2095-6533.2015.02.004

TN492

A

2095-6533(2015)02-0016-05