多态并行机上的3D图形渲染

韩俊刚, 姚 静, 李 涛, 黄虎才, 乔 虹, 延酉玫, 王鹏博

(1.西安邮电大学 计算机学院, 陕西 西安 710121; 2.西安邮电大学 电子工程学院, 陕西 西安 710121)

多态并行机上的3D图形渲染

韩俊刚1, 姚 静1, 李 涛2, 黄虎才1, 乔 虹2, 延酉玫1, 王鹏博1

(1.西安邮电大学 计算机学院, 陕西 西安 710121; 2.西安邮电大学 电子工程学院, 陕西 西安 710121)

针对多态同构阵列处理器，提出一种图形算法并行化的实现方法。该方法通过分析图形流水线中渲染算法的控制依赖、数据依赖关系，并对各个算法计算量进行估计，利用多态阵列处理机的能够结合不同类型的并行计算的特点，以处理器的负载均衡为依据，实现图形渲染的并行化计算。实验结果表明，该方法所实现的加速比按线性增长。

多态阵列机；并行计算；图形渲染；线程并行；操作并行；数据并行

计算机图形处理器(Graphics Processing Unit，GPU)被定义为集成了几何变换、光照、三角形装配和裁剪以及绘制引擎等功能的单芯片处理器，其具有每秒至少处理1千万个多边形的处理能力[1]。虽然GPU有如此高的处理能力，但是随着人类对视觉感受的不断追求，越来越多复杂细腻的图形图像出现在各类显示设备上[2]，如手机、平板电脑等。现在很多大型游戏都追求高清、逼真的画面，而渲染一个比较复杂的三维场景，需要有在一秒内处理数千万，甚至几亿、几十亿像素的能力。正是这种市场需求促使图形处理器向着众核处理器方向发展[3]。

算法的并行操作模式有单指令单数据流(Single Instruction Single Data, SISD)、单指令多数据流(Single Instruction Multiple Data, SIMD)、多指令单数据流(Multiple Instruction Single Data，MISD)以及多指令多数据流(Multiple Instruction Stream Multiple Data Stream，MIMD)四种[4]，目前GPU仅支持SIMD模式或者是其演化版SIMT模式[5]。一种新型同构多态阵列众核处理器(Polymorphic Array Architecture for Graphics and image processing ，PAAG)[6]可以结合数据级并行、线程级并行以及操作级并行[7]进行并行计算。PAAG架构对多种计算模式的支持能灵活对图形渲染管线进行动态配置，并且可以同时支持用SIMD和MIMD两种并行计算操作模式来实现对图形绘制的高效并行处理。针对串行方式的缺点，提出一种在PAAG架构上实现图形渲染管线的并行化方法。结合PAAG架构的灵活性，采用动态配置的方式对固定图形渲染管线[8]进行研究，并以串行方式进行实现，根据实验数据分析该方法的不足之处，以及造成这种结果的原因。

1 多态同构阵列处理器

多态同构阵列处理器PAAG由多个簇构成，每个簇为一个由PE构成的规则的二维阵列(2D array)，是一种较常见的阵列结构[9]。簇与簇之间采用分层的结构进行组织，与此同时，簇与簇之间也可以进行平面展开。PAAG中的最小处理单位是PE，它的结构如图1所示。

图1 处理单元结构

图1显示的PE结构图是由1个算术逻辑运算器(Arithmetic-Logic Unit, ALU)、1个路由器(Router,RU)、4个邻接通信共享存储、1个本地数据存储和1个本地指令存储组成。其中ALU每个时钟最多可同时发射两条指令；RU负责与远程处理器进行数据通信。

将PE按照阵列的方式进行管理，就是PAAG的一个基本簇，其结构如图2所示。

一个基本簇由一个4×4的阵列，16个PE以及控制这些PE的行控制器(Row Controller, CRi)、列控制器(Column Controller, CWj)和共享存储组成。PAAG阵列机基本簇的工作原理如下。

(1)相邻PE之间的通信可以通过东、西、南、北4个方向进行，可支持一个PE与4个PE同时进行通信。

(2)通信有阻塞模式和非阻塞模式两种方式。阻塞模式是当本级需要一个数据时，在上一级还没有发送数据过来的情况下，本级PE就会处于阻塞状态，直到接收到上一级PE发送的数据才会继续执行。这样可以保证数据的有效性，是解决同步问题的关键。

(3)不相邻的PE之间数据交互可以通过MOVET和MOVEF指令进行远程通信。MOVET和MOVEF指令也按照阻塞和非阻塞两种模式执行。

(4)每个PE都可以通过MVT和MVF指令在共享存储中进行数据的存取。

(5)PAAG支持SIMD和MIMD等多种并行编程方式。PAAG中的每个行控制器通过同时向同一行中的PE发送同一条指令来实现SIMD操作；而MIMD操作在PAAG中则体现为多个PE独立地执行各自的程序。PAAG通过结合数据级并行、操作级并行以及线程级并行等多种并行计算模式来充分挖掘程序中的并行性。

图2 PAAG阵列机基本簇结构

将多个基本簇进行统一管理，便形成了一个完整的PAAG处理器系统。其系统结构如图3所示。

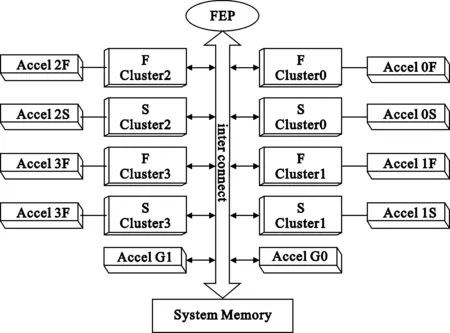
图3 PAAG系统整体结构

该系统包括1个与主处理器以及外部处理器接口的前端处理器FEP、4个S簇(S cluster0～3)、4个F簇(F cluster0～3)、外部存储器、片上存储器、各种专用加速器Accel(包括基本函数运算器、图形处理器、加速器等)和片上互联interconnect。S簇处理单元包含定点运算器，F簇包含浮点运算器和定点运算器两种。当执行应用程序时，前端处理器FEP是系统与CPU主处理器或者外部处理器的接口。

2 固定图形渲染管线

固定图形渲染管线中的渲染算法包括几何变换[10]与投影变换[11]、顶点染色[12]、剪裁[13]、消隐[14]、像素染色[15]以及片元操作，在时钟精确的PAAG仿真平台上分别对以上算法实现并运行，运行结果用直方图表示，该结果作为在处理器上进行线程分配的依据。

固定图形渲染管线方案是PAAG中的邻接通信共享存储可以将阵列中的PE以串行的方式有机地组织在一起，图4列举了PAAG单个簇中PE之间两种不同的串行互联方式，图4(a)串行路径以PE0为起始点，以PE12为终止点；图4(b)串行路径以PE0为起始点，以PE3为终止点。

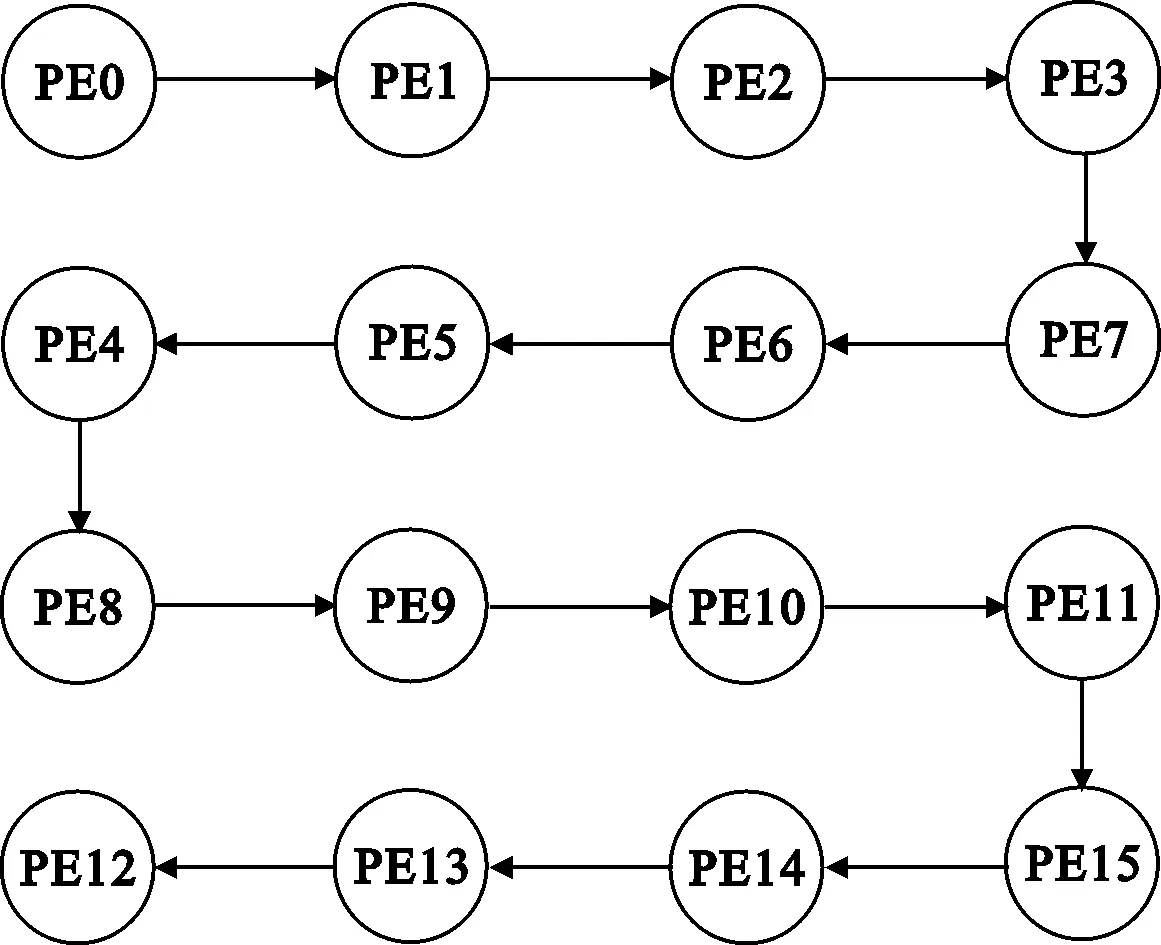
(a) PE0为起点,PE12为终点串行路径

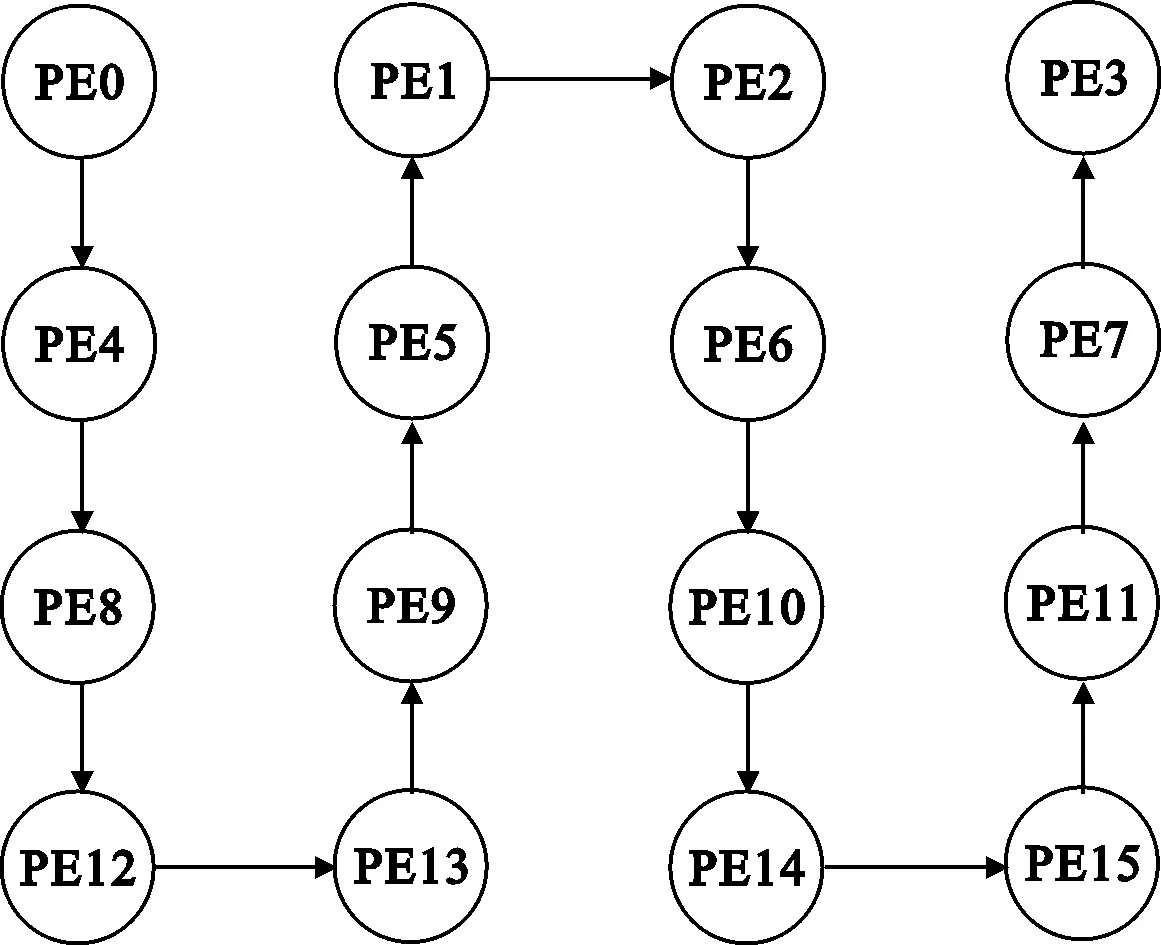
(b) PE0为起点,PE3为终点串行路径

固定图形渲染管线中的n个渲染子模块以串行的方式构成一条完整的渲染管线，为了获得各个渲染子模块的具体负载信息，将渲染子模块与簇中的PE进行了一对一的映射，各个渲染子模块之间的握手协议通过PE之间的邻接通信共享存储中的阻塞模式来完成，完整的图形渲染管线共需要7个PE来实现。引入光栅化硬件加速来提高整个系统的性能，具体架构如图5所示。

图5 渲染流水线

以光栅化为分界线，将渲染管线分为渲染前端与渲染后端，其中渲染前端以基本图元点、线、三角形作为基本处理元素，渲染后端以片元作为基本处理元素。以小三角形作为数据对象，在开启一盏灯以及对该三角形进行两个平行面裁剪的情况下，得到每个渲染部件所处理的基本元素的负载如图6所示。其中纵坐标表示某种渲染算法计算量占全部计算量的百分比，横坐标表示各个渲染部件。

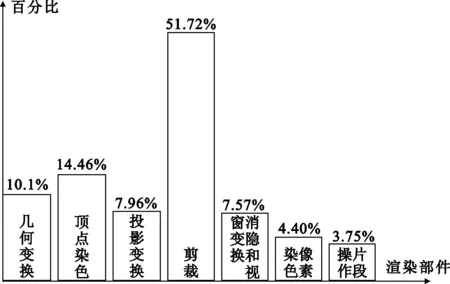
图6 经典流水线各部件负荷

由图6中的数据可以看见，渲染前端中除裁剪部件的负载远大于其它渲染子部件之外，其余渲染子部件的负载相差不大。剪裁模块负载重是因为多数图元都被剪裁，而且剪裁过的图元要重新计算节点属性并重新装配。

不同大小的基本图元在经典图形渲染管线中所表现出来的负载结果各不相同。如图7中的曲线(a)～(c)分别表示3种大小不同的三角形，顺序为从小到大。曲线(a)所对应的小三角形所产生的像素很少，因此渲染后端的负载较轻；而曲线(c)所对应的大三角形产生的像素较曲线(a)相比要多很多，渲染后端的负载相对来说会比较重。

由图7中各个渲染部件的负载量可以看出，类似于曲线(a)中大小的三角形，其负载瓶颈表现在裁剪阶段，负责裁剪操作的处理器PE3在进行具体操作过程中，其他处理器绝大部分时间处于空闲状态；对于曲线(b)和曲线(c)中大小的三角形，其负载瓶颈出现在渲染过程的后端。

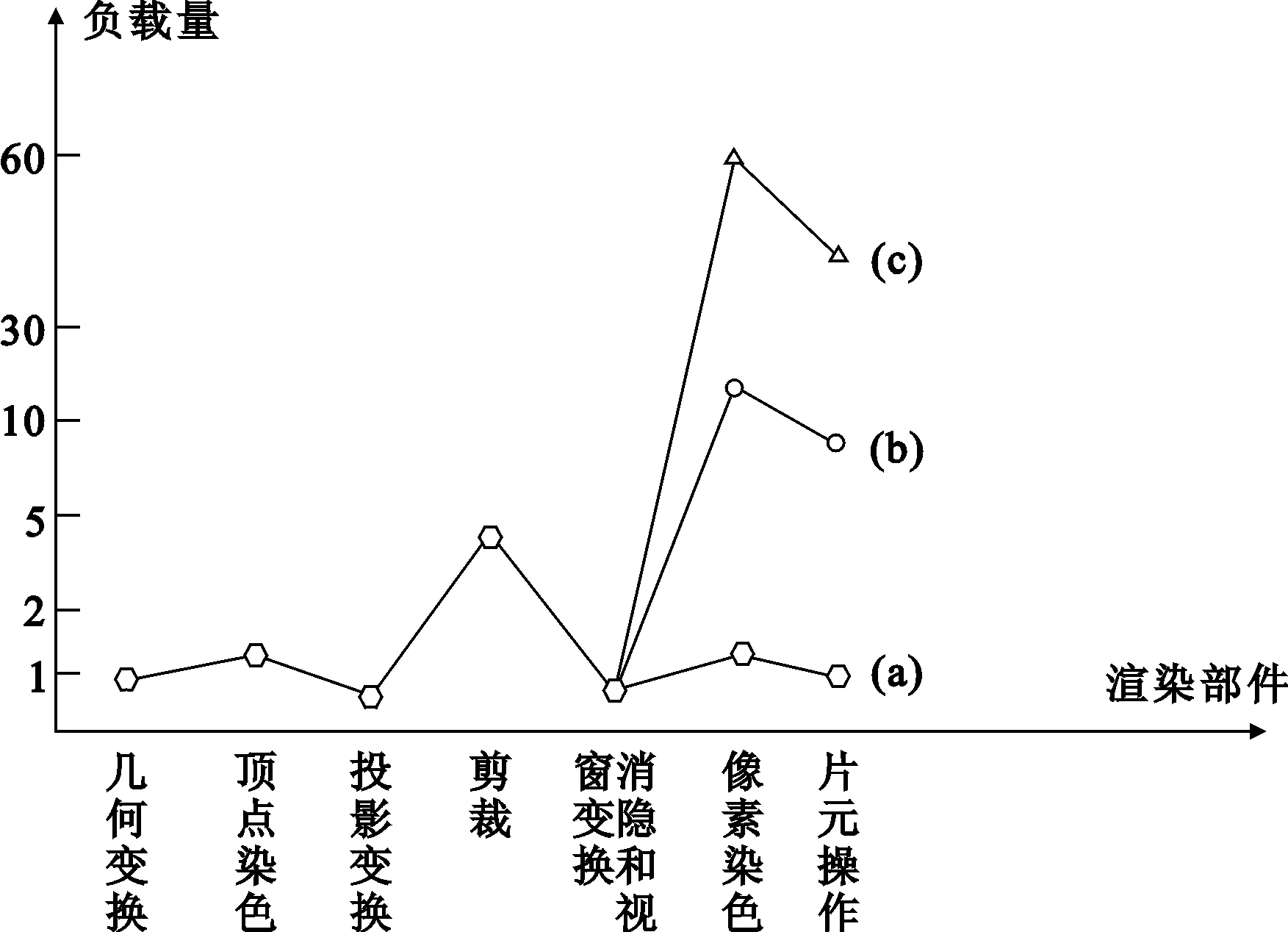
图7 不同类型三角形的负载

为了实现渲染管线的负载均衡，将负载过重的渲染子模块进行功能分块，以流水线的方式进行组合来提高操作并行度。将顶点渲染子模块扩展至2个PE中，裁剪部件扩展至3个PE，像素染色与片元操作各采用2个PE，架构如图8所示。

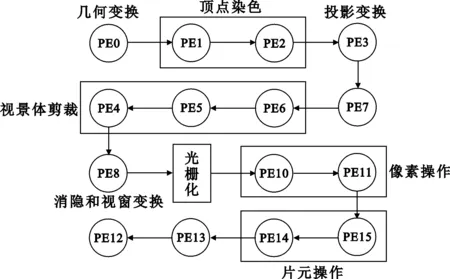
图8 经过负载均衡的图形渲染管线

负载均衡化后的渲染架构所得到的负载表现如图9所示。

图9 负载均衡后不同类型三角形的负载

由图9中各个渲染部件的负载量可以看见，对于小三角形，其负载瓶颈转移到了渲染后端；对于中、大三角形，其负载瓶颈仍然在渲染后端，尽管经过负载均衡后的负载瓶颈系数比原来缩小了将近一倍。但负载均衡比较困难，难以得到均等的操作分布。

将各渲染子模块采用不同数量PE进行负载均衡，所得到的性能分布如图10所示，其中曲线(1)～(7)分别表示几何变换、顶点染色、投影变换、剪裁、消隐和视窗变换、像素染色和片段操作。

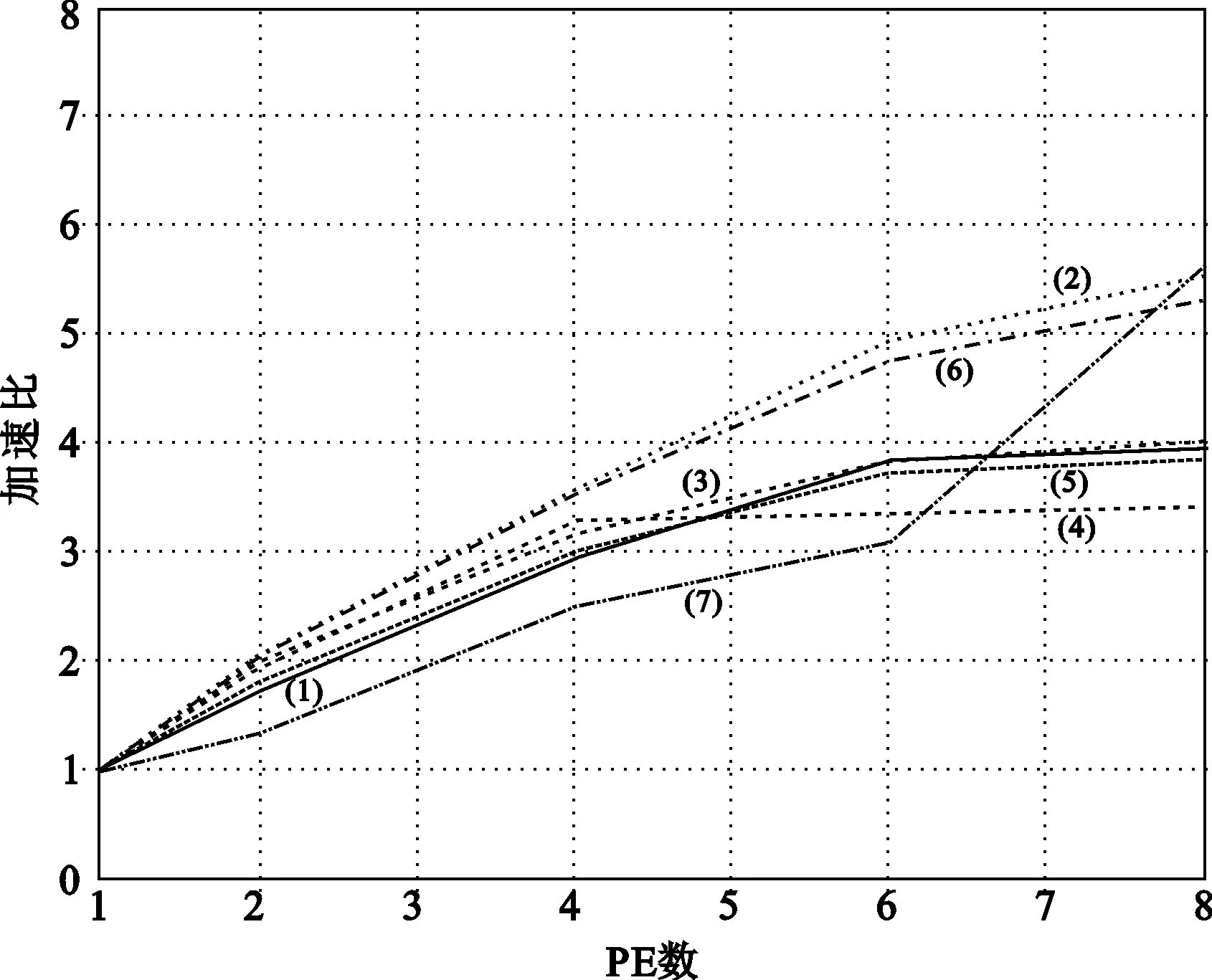
图10 不同数量PE的各渲染模块负载均衡性能统计

由图10中数据变化趋势可以看见，顶点染色和像素染色的分割较好，加速度接近线性。其它渲染部件则很难分割平衡，加速度效果并不理想。在PE个数为8时，除了顶点染色渲染子模块之外，其余渲染子模块的性能已基本接近峰值。此时所得到的性能分布如图11所示。

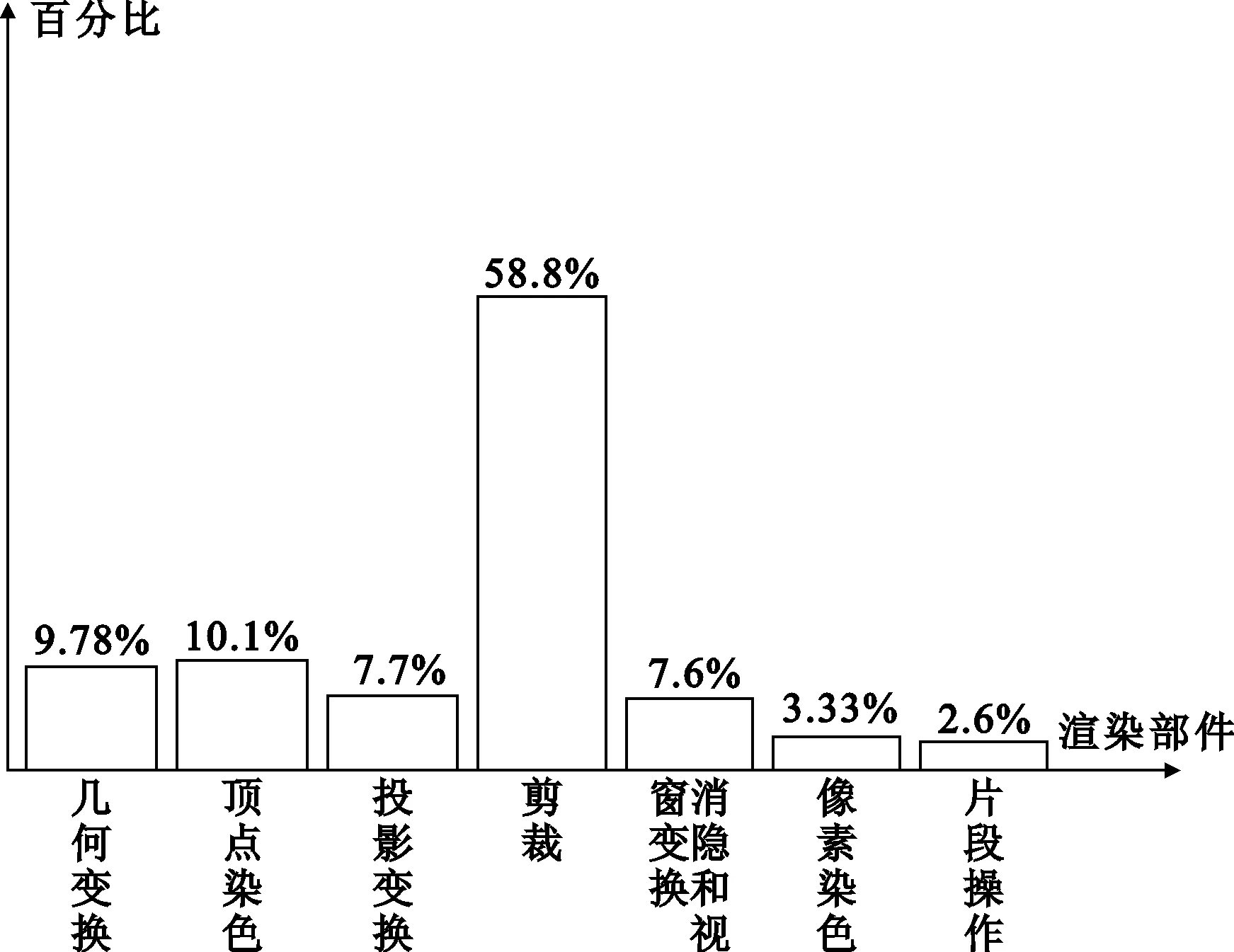
图11 8个PE各渲染子模块的负载分布

基于以上结果，将负载均衡方案进行扩展，记S(i)为图形渲染管线中第i个渲染子模块所分配的PE数，L(i)为第i个渲染子模块的负载量，因此每个渲染子模块中的单个PE的负载量可表示为

L(i)pe=L(i)/S(i)。

从图10可以看出，在S(i)小于8时，S(i)与渲染性能的递增成正比关系，当S(i)的值达到8后，渲染子部件的性能将逐渐达到峰值，而当S(i)的取值越来越大时，PE之间的数据通信与PE的有效执行的比例逐渐增大，S(i)的增加反而会导致渲染性能下降。这是因为这种单PE处理方式中，每个渲染部件的负载差距较大，导致获得的加速比有限。且这种严重的负载不均衡现象降低了整条图形渲染管线的处理效率。

3 图形并行渲染设计及验证

为了提高程序的处理效率，充分发挥PAAG的并行计算能力，以PAAG阵列处理器架构为渲染平台，以PAAG中的每个PE作为基本渲染单元，采用基于MIMD的统一渲染[16]执行方式来实现对图形的渲染。

3.1 PAAG中的图形并行渲染架构

将PAAG中的PE阵列以虚拟宏单元(Virtual Macro PE, VMPE)的方式进行组织管理，每个VMPE由n个PE构成(n≥1)，n的取值可以灵活地进行配置，以便根据具体需要来支持多种并行计算模式。以单个VMPE作为基本渲染单元，图形渲染中的每次渲染请求由VMPE来实现，VMPE直接由簇控制器来管理。单个虚拟宏单元VMPE所能获得的加速比直接决定了PAAG阵列处理器的加速比。

在操作级并行计算中，通过根据渲染程序的控制依赖以及负载来对其进行分块，每个块表示一个渲染片段，所得到的块根据控制依赖关系映射到虚拟宏单元VMPE的不同PE上，渲染片段的具体大小由渲染程序以及虚拟宏单元VMPE中的PE个数n决定。

每个PE通过执行一个渲染片段来完成对整个算法的实现，例如将VMPE的大小设置为n=2，图12为将片元操作映射到两个PE上的一种方法。

图12 片元操作在n=2的VMPE中的实现

在图12中n=2的实现方法中，当PE1接收到一个片元后，完成对片元的剪裁测试、Alpha测试、深度测试、模板测试等4种基本测试，之后通过邻接互联存储将通过的片元传输给PE0，PE0紧接着对片元执行混合和逻辑操作。将VMPE的n值扩展为4后，所得到的映射关系如图13所示，这时，每个PE对片元所执行的操作相对于n=2时平均下来将会成倍减少。

图13 片元操作在n=4的VMPE中的实现

在线程级并行中，VMPE中的n个PE各自执行一段完整的渲染程序，每段渲染程序以独立的线程方式执行，不需要对程序进行分块处理。图形渲染中的几何渲染、顶点渲染以及像素渲染等分别被当作一个独立的线程，PE之间独立操作而互不影响，在一个VMPE中可同时处理n个顶点，VMPE中的每个PE完成对一个顶点的所有渲染操作，如图14所示。

图14 顶点渲染操作的线程级并行实现

当VMPE中的n=1时，VMPE与单个PE等价，此时PAAG中VMPE所进行的操作级并行操作将退化为PAAG阵列中的线程级并行操作。

3.2 实验结果验证

将VMPE的n分别设置为1、2、4、6、8，将图形渲染管线中的各个渲染算法——几何变换、顶点染色、投影变换、剪裁、消隐和视窗变换、像素染色和片段操作，分别进行线程级并行(Thread-Level Parallelism ，TLP)和操作级并行(Operation Level Parallel，OLP)实现，并将最终的实验结果进行比较，得到如图15所示的性能对比结果。

由图15中的结果可以看见，以上渲染算法的线程级并行加速度，基本都可以实现线性增长，当PE数为8时，其加速比可以达到7.8左右。但是操作级并行的加速度相对来说要差一些，只有顶点染色、像素染色和片元操作的加速比在8个PE时达到了5.0以上，几何变换，投影变化、剪裁、视窗变换和消隐的加速比都只有4.0左右。

实验数据表明，统一渲染中线程级并行的处理效率要优于粗粒度操作级并行，这是因为在粗粒度操作级并行中，人为地对程序进行分割，并不能保证每个PE上的负载完全均衡。由于加速度的提升由负载最重的PE所决定，这种负载不完全均衡的性质直接影响了所能获得的加速比。

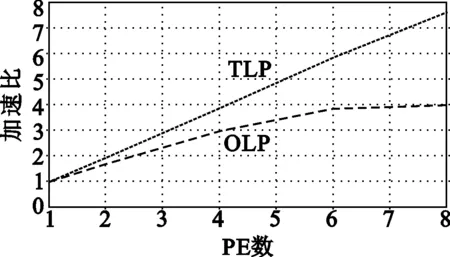
(a) 几何变换

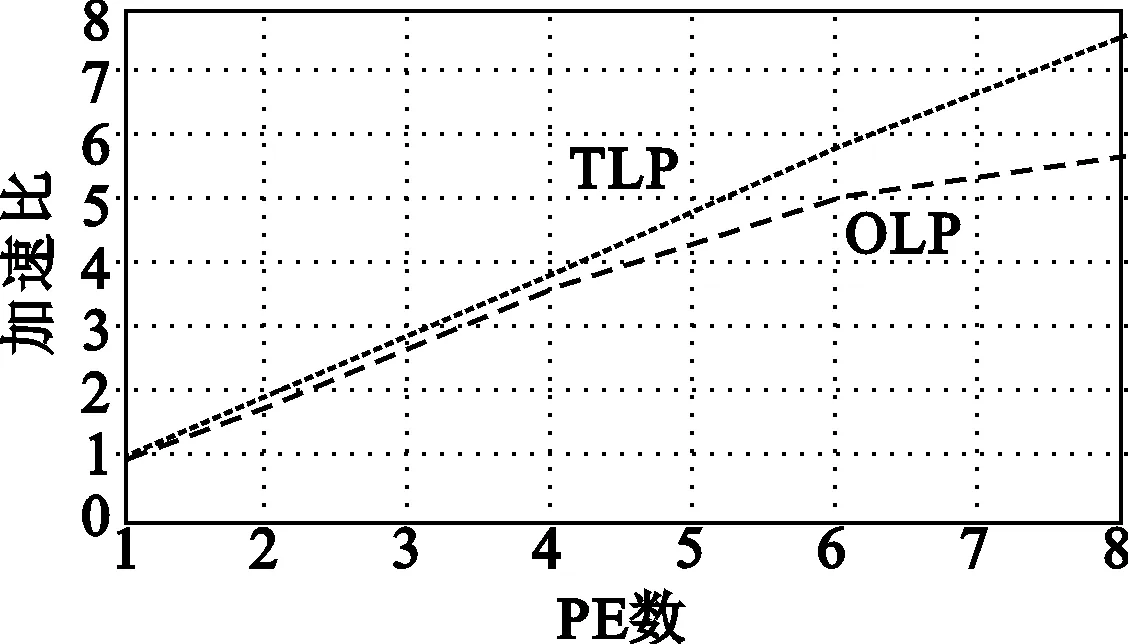
(b) 顶点染色

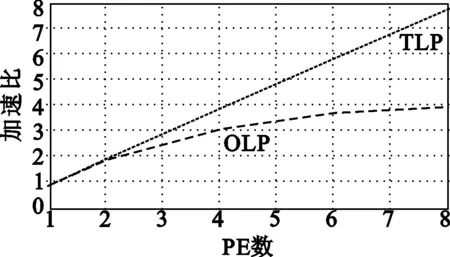
(c) 投影变换

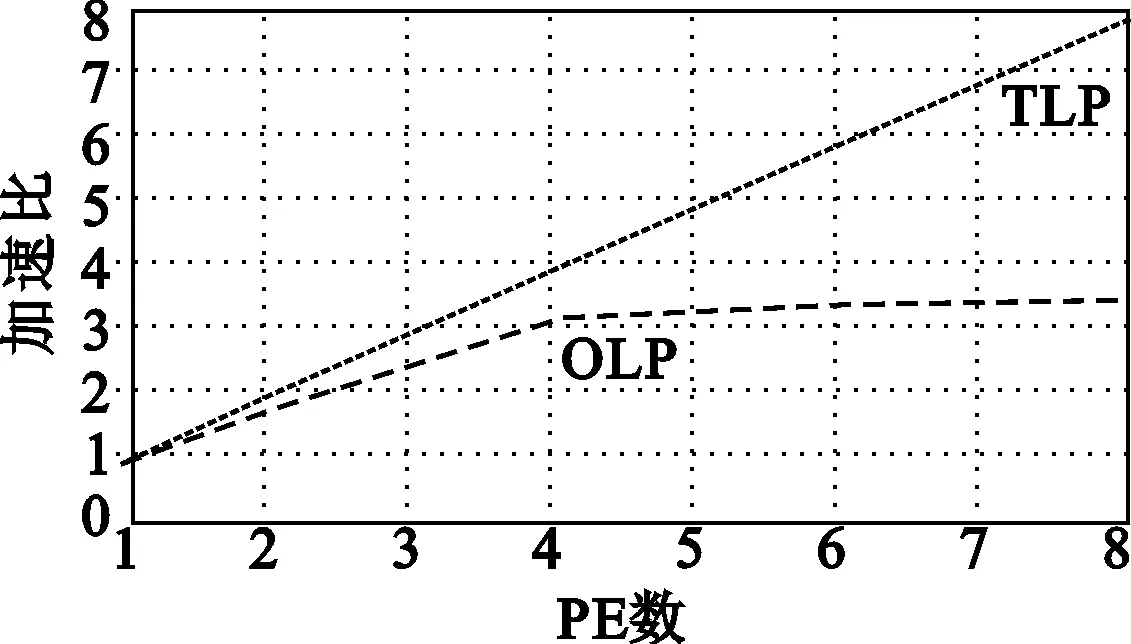
(d) 剪裁

(e) 消隐和视窗变换

(f) 像素染色

(g) 片元操作

4 结束语

利用PAAG所提供的丰富而灵活的并行计算模式，分别实现了固定图形渲染管线以及图形的统一渲染中的两种不同的执行方式，实验数据说明了在PAAG中实现固定渲染管线的不足，并比较了PAAG在统一渲染模式中两种不同并行计算模式的性能加速比。实验结果表明，经过并行化后的程序处理数据的速度得到显著的提高。

[1] GPU Changes Everything[EB/OL].(2010-10-21) [2014-09-26]http://www.nvidia.com/object/gpu.html.

[2] Tomas A, Eric H, Hoffman N. Real-Time Rendering[M]. 3nd Edition, Florida:CRC Press, 2012:189-192.

[3] 韩俊刚, 刘有耀, 张晓.图形处理器的历史现状和发展趋势[J]. 西安邮电学院学报，2011,16(3):61-64.

[4] Flynn M. Some Computer Organizations and Their Effectiveness[J]. IEEE Transactions on Computers, 2010, (9):948-960.

[5] Grot B, Hestness J, Keckler S W, et al. Kilo-NOC: A heterogeneous network-on-chip architecture for scalability and service guarantees[C]//Computer Architecture (ISCA), 2011 38th Annual International Symposium on. Piscataway: IEEE Press, 2011:401-412.

[6] Li Tao, Xiao Ling-zhi, Huang Hui-cai, et al. PAAG: A Polymorphic Array Architecture for Graphics and Image Processing[C]//Parallel Architectures, Algorithms and Programming (PAAP), 2012 Fifth International Symposium on. Piscataway: IEEE Press, 2012: 242-249.

[7] David A P, John L H. Computer architecture: a quantitative approach[M]. 4th Ed, Massachusetts:Morgan Kauffmann, 2006:83-85.

[8] Dave Shreiner The Khronos OpenGL ARB working Group. OpenGL编程指南[M].7版.北京：机械工业出版社，2010:424-425．

[9] 李涛，肖灵芝.面向图形和图像处理的轻核阵列机结构[J].西安邮电学院学报,2012，17(3)：41-47.

[10] 孙加广, 胡事民. 计算机图形学基础教程[M]. 2版. 北京：清华大学出版社, 2009:58-67.

[11] Edward A. Interactive Computer Graphics: A Top-Down Approach Using OPENGL[M].4th Ed, New Jersey:Addison Wesley, 2006:351-364.

[12] Shreiner D B. The Khronos OpenGL ARB Working Group. OpenGL programming guide: the official guide to learning OpenGL, versions 3.0 and 3.1[M]. 7th Ed, London: Pearson Education, 2009:156-158.

[13] Edward A. Interactive Computer Graphics: A top-Down Approach with Shader-Based OpenGL[M]. New Jersey: Addison Wesley, 2011:89-94.

[14] 夏小玲. 三维消隐算法研究[J]. 东华大学学报：自然科学版， 2002, 28(2):137-142.

[15] 董梁, 刘海, 韩俊刚. 图形处理器中光照和纹理映射的设计与仿真实现[J].计算机科学, 2011, 38(2):284-301.

[16] Kim T, Kim J, Hur H. A unified shader based on the OpenGL ES 2.0 for 3D mobile game development[J]. Lecture Notes in Computer Science, 2007,4469(6): 898-903.

[责任编辑:祝剑]

3D graphics rendering on a polymorphic computer

HAN Jungang1, YAO Jing1, LI Tao2, HUANG Hucai1,QIAO Hong2, YAN Youmei1, WANG Pengbo1

(1.School of Computer Science, Xi’an University of Posts and Telecommunications, Xi’an 710121, China； 2. School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

A new method of graphics parallelizing algorithm on Polymorphic Array Architecture for Graphics processor is presented in this paper. In this method, each algorithm is evaluated by analyzing the control dependencies and data dependencies of the rendering algorithms in graphics pipeline, and the amount of calculations in each algorithm are estimated. Based on the load balancing of processor, the calculation scheme of parallel graphics rendering on PAAG is made by using the characteristics that PAAG can combine different types of parallel computing. Experimental results show that linear speedup can be obtained by this method.

polymorphic array processor, parallel computing, graphics rendering, thread level parallel, operation level parallel, data level parallelism

2014-12-04

国家自然科学基金重大项目(61136002)

韩俊刚(1943-)，男，教授，从事软件和硬件的形式化验证、图形处理器和新型计算机体系结构研究。E-mail: hjg@xupt.edu.cn 姚静(1989-)，女，硕士研究生，研究方向为软件设计与测试。E-mail: yaojing19890325@sina.com

10.13682/j.issn.2095-6533.2015.02.001

TP302

A

2095-6533(2015)02-0001-07